用go语言实现树和哈希表算法
算法复杂度
判断一个算法的效率通常基于其计算复杂度,这主要与算法访问输入数据的次数有关。计算机科学中常用大O表示法来描述算法的复杂度。例如,O(n)的算法只需访问一次输入数据,因此优于O(n²)的算法,后者则优于O(n³)的算法,依此类推。最差的算法是O(n!)的复杂度,当输入数据超过300个元素时,这样的算法几乎无法使用。
在Go语言中,大多数内建类型的查找操作(如通过键值查找map中的元素或访问数组元素)都具有常数时间复杂度,表示为O(1)。这意味着内建类型通常比自定义类型更快,除非你希望对底层行为进行完全控制,否则应优先选择使用内建类型。
不仅如此,不同的数据结构效率各不相同。通常,数组操作比map操作要快,但map的多功能性使它具有独特的优势。因此,开发者在选择数据结构时需权衡这些特性。
Go中的二叉树
二叉树简介
二叉树是一种数据结构,每个节点最多有两个子节点,即一个节点可以与最多两个其他节点相连。二叉树的根节点是树的第一个节点。树的深度(也称为高度)是从根节点到某个节点的最长路径,而某个节点的深度是该节点到根节点的边数。没有子节点的节点称为叶子节点。
当一棵树的最长路径与最短路径之间的差值不超过1时,称其为平衡树。如果不满足这一条件,则为不平衡树。树的平衡操作通常较为复杂且耗时,因此最好在树创建时保持其平衡,特别是在节点数量较多的情况下。
二叉树的实现
在Go中,二叉树的实现可以通过结构体定义节点。下面是实现一个简单二叉树的代码,并带有中文注释。
package mainimport ("fmt""math/rand""time"
)// 定义二叉树节点结构
type Tree struct {Left *Tree // 左子节点Value int // 节点的值Right *Tree // 右子节点
}// 遍历二叉树
func traverse(t *Tree) {if t == nil {return}traverse(t.Left) // 递归遍历左子树fmt.Print(t.Value, " ") // 打印当前节点的值traverse(t.Right) // 递归遍历右子树
}// 创建二叉树并填充随机值
func create(n int) *Tree {var t *Treerand.Seed(time.Now().Unix()) // 初始化随机数种子for i := 0; i < 2*n; i++ {temp := rand.Intn(n * 2)t = insert(t, temp) // 插入随机值}return t
}// 插入节点到二叉树中
func insert(t *Tree, v int) *Tree {if t == nil {return &Tree{nil, v, nil} // 创建根节点}if v == t.Value {return t // 如果值已存在,不做操作}if v < t.Value {t.Left = insert(t.Left, v) // 递归插入到左子树return t}t.Right = insert(t.Right, v) // 递归插入到右子树return t
}func main() {tree := create(10)fmt.Println("树的根节点值为:", tree.Value)traverse(tree)fmt.Println()// 插入新值并再次遍历tree = insert(tree, -10)tree = insert(tree, -2)traverse(tree)fmt.Println()fmt.Println("树的根节点值为:", tree.Value)
}
运行结果:
树的根节点值为: 18
0 3 4 5 7 8 9 10 11 14 16 17 18 19
-10 -2 0 3 4 5 7 8 9 10 11 14 16 17 18 19
树的根节点值为: 18
二叉树的优势
二叉树特别适合用于表示层次结构的数据,因此在编译器解析程序代码时,广泛采用二叉树。此外,二叉树是天然有序的,只需插入元素到正确位置,树结构就会保持有序。然而,删除树中的元素相对复杂,因为需要维护树的结构。
当二叉树是平衡的,其查找、插入和删除操作的时间复杂度大约为O(log n),其中n是树中元素的数量。例如,一个包含100万个元素的平衡树,其高度大约为20,这意味着可以在不到20步内访问到树中的任意节点。
二叉树的主要缺点在于其结构取决于插入元素的顺序。如果树的键值较长且复杂,插入和查找操作可能会变慢。此外,如果树不平衡,树的性能将变得不可预测。
哈希表在Go中的应用
哈希表的概念
哈希表是一种存储键值对的数据结构,它通过哈希函数计算出一个索引,从而定位数据。一个好的哈希函数需要能够产生均匀分布的哈希值,以避免哈希冲突。
Go中的哈希表实现
下面展示了如何在Go中实现一个简单的哈希表:
package mainimport ("fmt"
)// 定义哈希表的大小
const SIZE = 15// 定义哈希表的节点结构
type Node struct {Value intNext *Node
}// 定义哈希表结构
type HashTable struct {Table map[int]*NodeSize int
}// 哈希函数
func hashFunction(i, size int) int {return i % size
}// 插入数据到哈希表
func insert(hash *HashTable, value int) int {index := hashFunction(value, hash.Size)element := Node{Value: value, Next: hash.Table[index]}hash.Table[index] = &elementreturn index
}// 遍历哈希表
func traverse(hash *HashTable) {for k := range hash.Table {if hash.Table[k] != nil {t := hash.Table[k]for t != nil {fmt.Printf("%d -> ", t.Value)t = t.Next}fmt.Println()}}
}func main() {// 创建哈希表table := make(map[int]*Node, SIZE)hash := &HashTable{Table: table, Size: SIZE}fmt.Println("哈希表的大小为:", hash.Size)// 向哈希表插入数据for i := 0; i < 120; i++ {insert(hash, i)}// 遍历并打印哈希表traverse(hash)
}
运行结果:
哈希表的大小为: 15
105 -> 90 -> 75 -> 60 -> 45 -> 30 -> 15 -> 0 ->
110 -> 95 -> 80 -> 65 -> 50 -> 35 -> 20 -> 5 ->
...
哈希表的优势
哈希表的最大优势在于查找速度快。当哈希表有n个键和k个桶时,查找时间复杂度从O(n)降低到O(n/k),即使哈希表中有大量元素,查找效率也能保持在较低的时间复杂度内。
补充知识点
-
二叉树的平衡与自平衡树:虽然普通二叉树的性能取决于插入顺序,但一些自平衡树(如AVL树和红黑树)通过自动调整树的结构,确保即使在最差情况下也能维持较优的性能。
-
哈希碰撞处理:在哈希表中,多个键可能会映射到同一个索引,这被称为哈希碰撞。常用的碰撞处理方法有链地址法和开放地址法。在链地址法中,每个桶包含一个链表,用于存储冲突的键值对。
通过本文的讲解,相信大家对数据结构如二叉树和哈希表在Go中的应用有了更深入的理解。掌握这些基础结构,不仅能提升代码效率,还能为复杂项目的实现打下坚实的基础。
相关文章:

用go语言实现树和哈希表算法
算法复杂度 判断一个算法的效率通常基于其计算复杂度,这主要与算法访问输入数据的次数有关。计算机科学中常用大O表示法来描述算法的复杂度。例如,O(n)的算法只需访问一次输入数据,因此优于O(n)的算法,后者则优于O(n)的算法&…...

基于SpringBoot+Vue+MySQL的校园健康驿站管理系统
系统展示 用户前台界面 管理员后台界面 系统背景 本文设计并实现了一个基于SpringBoot后端、Vue前端与MySQL数据库的校园健康驿站管理系统。该系统旨在通过数字化手段,全面管理学生的健康信息,包括体温监测、疫苗接种记录、健康状况申报等,为…...

深入理解MATLAB中的事件处理机制
在MATLAB中,事件处理机制是一种强大的工具,它允许对象之间的交互和通信。这种机制基于观察者设计模式,其中一个对象(观察者)监听另一个对象(发布者)的状态变化。当发布者的状态发生变化时&#…...

线程--线程同步
这里写目录标题 同步概念线程同步概念数据混乱原因 互斥量原理锁的注意事项1、cpu时间轮片2、建议锁总结 使用锁来管理线程同步问题产生主要函数init、destorylock、unlock代码注意事项(锁的粒度) try锁死锁出现原因图解 读写锁特性图解函数总览init、de…...

【QT】Qt窗口
欢迎来到Cefler的博客😁 🕌博客主页:折纸花满衣 🏠个人专栏:QT 目录 👉🏻菜单栏设置👉🏻QToolBar练习 👉🏻QStausBar👉🏻Q…...

场外个股期权怎么给股票加杠杆?
今天期权懂带你了解场外个股期权怎么给股票加杠杆?场外期权交易通过向证券公司支付一定额度的股票期权费,然后买入大额的股票持仓,从而实现的杠杆交易。 买入看涨期权 操作:支付权利金购买看涨期权。 杠杆作用: 期…...

【Docker部署ELK】(7.15)
1、拉取镜像 docker pull docker.elastic.co/elasticsearch/elasticsearch:7.15.0 docker pull docker.elastic.co/kibana/kibana:7.15.0 docker pull docker.elastic.co/logstash/logstash:7.15.02、配置文件(解压资源到D盘DOCKER目录下) 2.1 配置文件…...

UE4_后期处理_后期处理材质及后期处理体积一
后期处理效果 在渲染之前应用于整个渲染场景的效果。 后期处理效果(Post-processing effect)使美术师和设计师能够对影响颜色、色调映射、光照的属性和功能进行组合选择,从而定义场景的整体外观。要访问这些功能,可以将一种称为…...

【PyQt6 应用程序】基于QtDesigner做一个用户登录页面
在当今的软件开发领域,用户界面(UI)设计和后端编程是创建现代、互动应用程序的两大重要组成部分。尤其是在开发具有用户登录功能的应用程序时,不仅要注重外观和用户体验的设计,还要确保后端逻辑的安全性和可靠性。 本文将介绍如何使用PyQt6框架结合UI设计,实现一个简单而…...

Ollama—87.4k star 的开源大模型服务框架!!
这一年来,AI 发展的越来越快,大模型使用的门槛也越来越低,每个人都可以在自己的本地运行大模型。今天再给大家介绍一个最厉害的开源大模型服务框架——ollama。 项目介绍 Ollama 是一个开源的大语言模型(LLM)服务工具…...

MySQL表的操作与数据类型
目录 前言 一、表的操作 1.创建一个表 2.查看表的结构 3.修改表 4.删除一个表 二、 MySQL的数据类型 0.数据类型一览: 1.整数类型 2.位类型 3.小数类型 4.字符类型 前言 在MySQL库的操作一文中介绍了有关MySQL库的操作,本节要讲解的是由库管理的结构——…...

mysql把某一个字段的值中的aa,替换成bb
UPDATE my_table SET my_column REPLACE(my_column, aa, bb); 例 假设my_table表在替换前的数据如下: idmy_column1hello aa2world aa aa3no aa here 执行上述UPDATE语句后,my_table表的数据将变为: idmy_column1hello bb2world bb b…...

【系统架构设计师】原型模式详解
原型模式详解 1. 什么是原型模式? 原型模式(Prototype Pattern)是一种创建型设计模式,它允许通过复制已有的对象来创建新的对象,而不是通过类实例化来创建新对象。通过这种方式,原型模式能够减少创建对象的开销,尤其是当对象的创建过程非常复杂或者耗费资源时。原型模…...

Spring @Async 深度解读:默认线程池执行器的配置与优化
在Spring中,Async注解用于异步执行方法。默认情况下,Async注解的任务是由一个线程池执行的。然而,这个默认的线程池是如何初始化的呢?本文将深入探讨这一过程,帮助你理解Spring异步任务背后的线程池执行器的初始化原理…...
手把手教你用护核纪元地心护核者用服务器开服联机
1、购买后登录服务器面板(百度莱卡云面板) 登录面板的信息在绿色的登陆面板按键下方,不是你的莱卡云账号 进入控制面板后会出现正在安装的界面,安装大约3分钟(如长时间处于安装中请联系我们的客服人员) 2、…...

Log4j 1.x如何升级到Log4j 2.x
Log4j 1.x升级到Log4j 2.x是一个涉及多个步骤的过程,主要包括删除旧版本、添加新版本依赖、配置新版本的配置文件等。以下是一个详细的升级步骤指南: 一、准备阶段 了解当前项目依赖: 检查项目中所有使用Log4j 1.x的地方,包括ja…...

CloudFlare问题与CDN问题
昨天将腾讯云的解析转移到Cloudflare中了,结果今天发现网站崩了,显示重定向次数过多,昨天估计是因为浏览器缓存,所以没有发现问题 问题一:强制HTTPS 当时看到CloudFlare的强制https时就想到了我的宝塔面板也开着强制h…...
[Linux]:文件(上)
✨✨ 欢迎大家来到贝蒂大讲堂✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 所属专栏:Linux学习 贝蒂的主页:Betty’s blog 1. C语言文件操作 C语言文件操作接口如下,详情可参照——C语言文…...
)
flutter开发多端平台应用的探索 下 (跨模块、跨语言通信之平台通道)
前文 Flutter 是一个跨平台的开发框架,它允许开发者使用相同的代码库来构建 iOS、Android、Web 和桌面应用程序。 上文flutter开发多端平台应用的探索 上(基本操作)-CSDN博客列举了一些特定平台的case(桌面端菜单,鼠…...

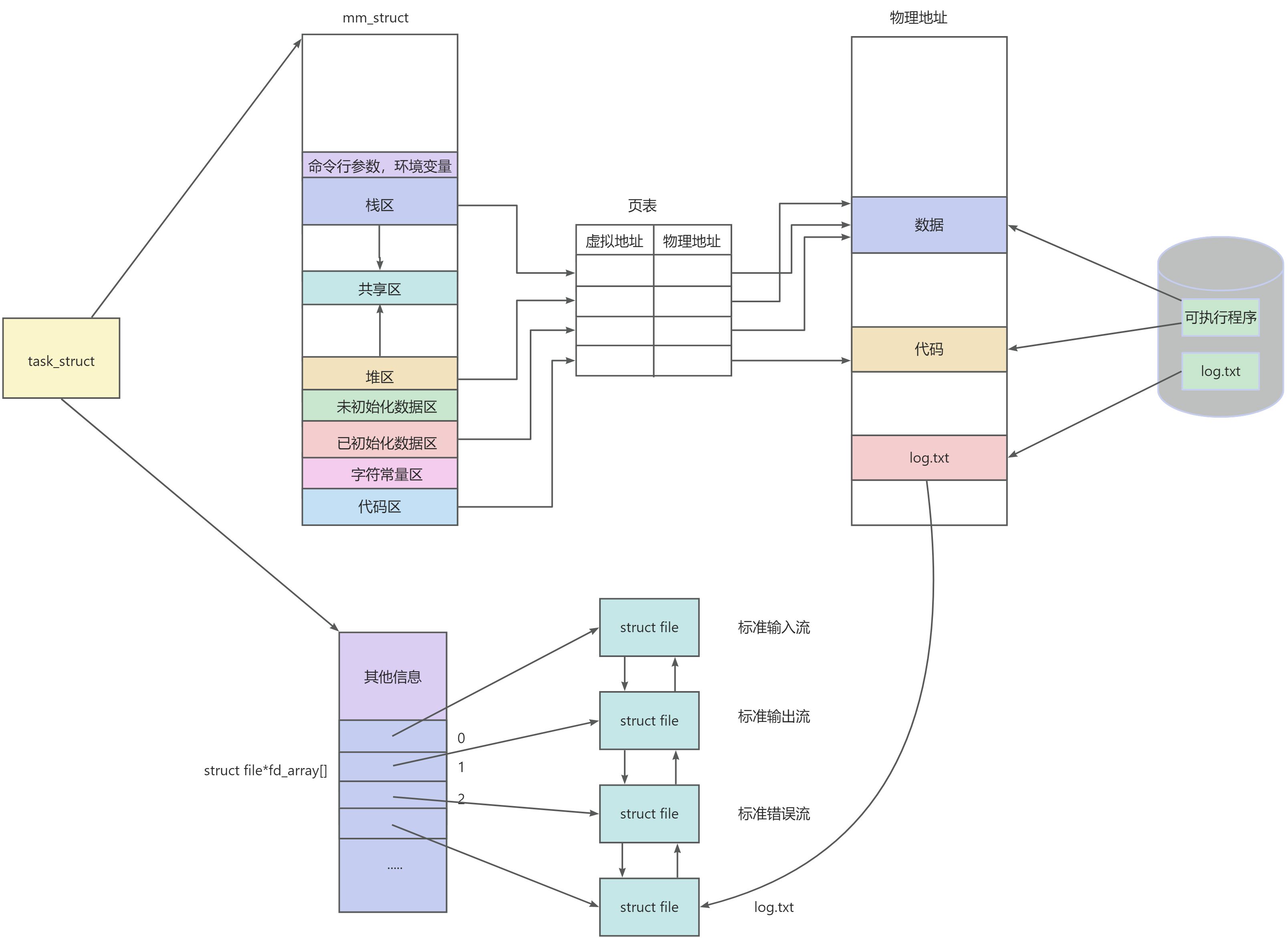
第15-02章:理解Class类并获取Class实例
我的后端学习大纲 我的Java学习大纲 1、Java反射机制原理图: 源代码通过Javac编译得到字节码文件,当我执行到new一个对象的时候,字节码文件会通过ClassLoader被加载,然后得到一个Class类对象,存放在堆中,加…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
