走进低代码报表开发(一):探秘报表数据源
|
|
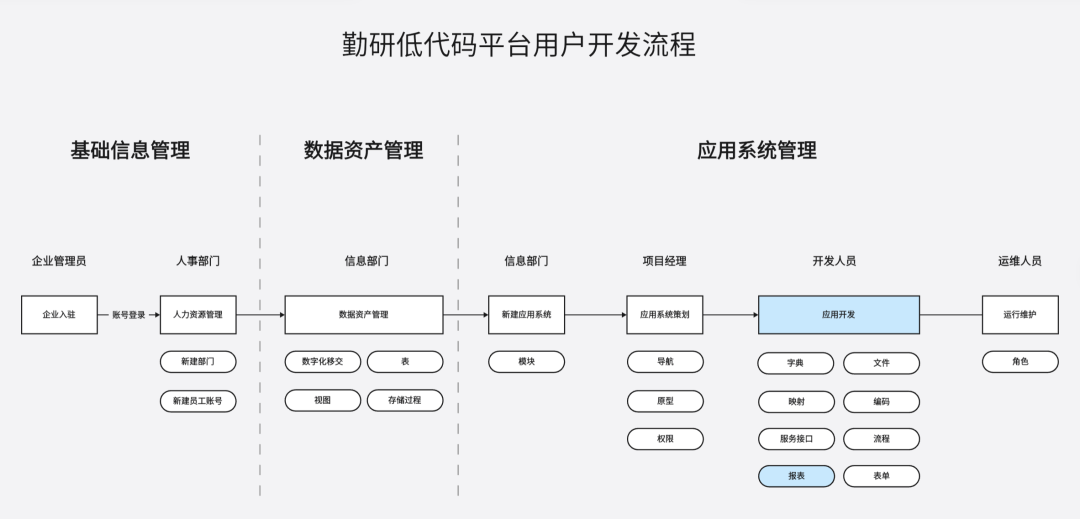
在前文当中,我们对勤研低代码平台的流程设计功能进行了介绍。接下来,让我们一同深入了解在企业日常运营中另一个极为常见的报表功能。在当今数字化时代,高效的报表生成对于企业的决策至关重要。勤研低代码开发平台能够以卓越的性能和便捷的操作,为用户带来全新的报表开发体验。
|
|
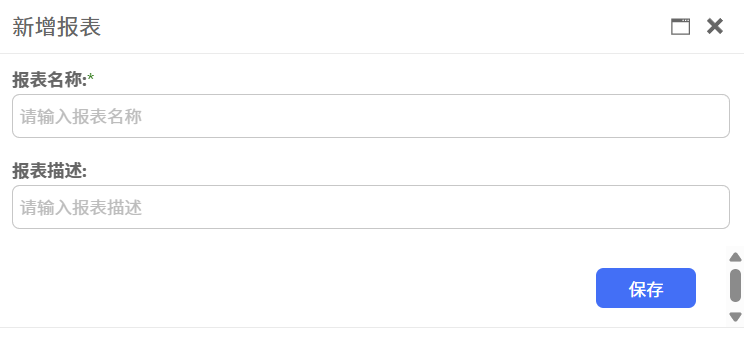
一、快速创建报表
勤研低代码开发平台让报表创建变得极为简单。用户仅需填写报表名称和描述,即可完成报表的创建。无需复杂的编程知识和繁琐的操作步骤,大大提高了工作效率。
|
|
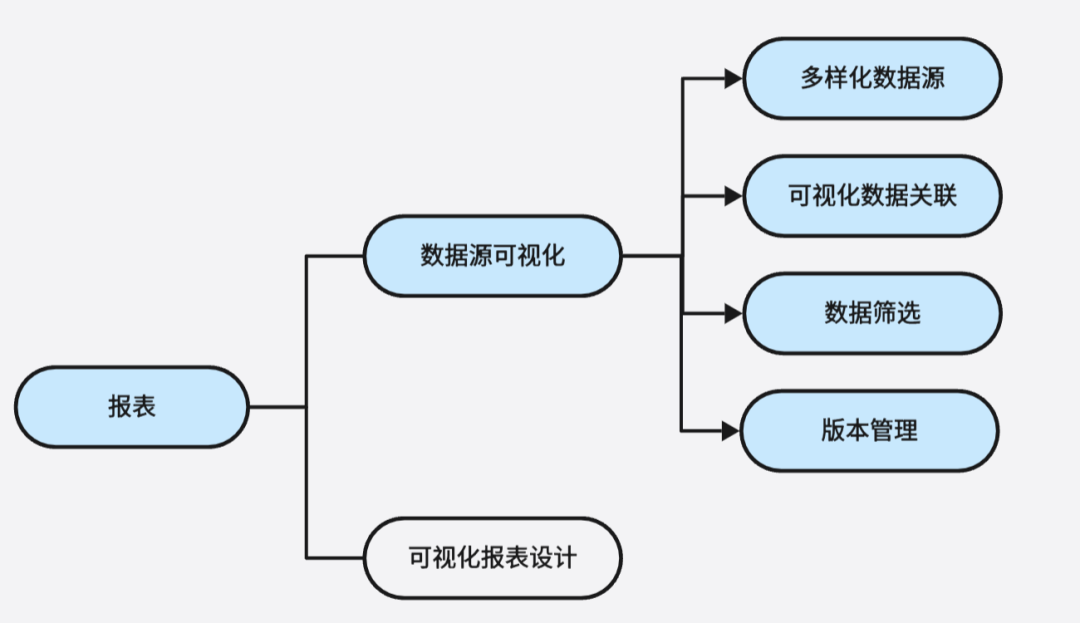
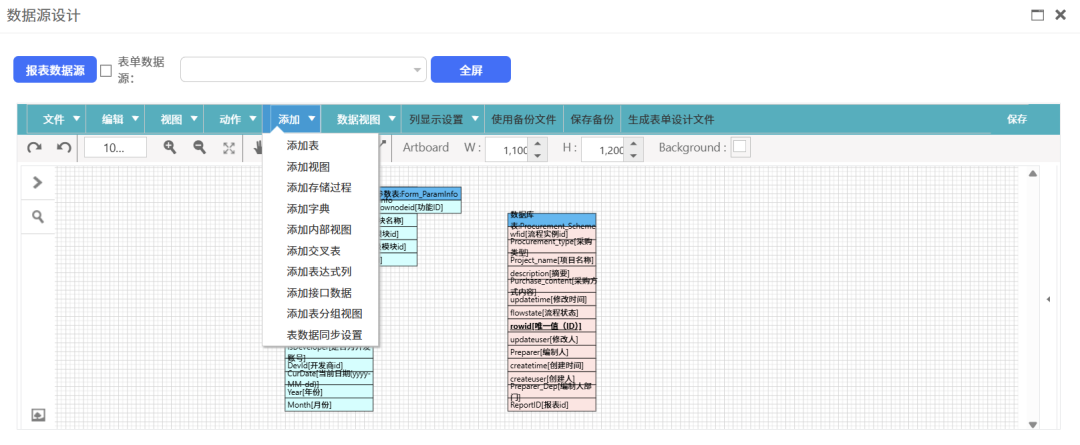
二、多样化的数据源支持
完成报表创建后,用户可通过可视化的界面添加报表的数据源。平台的报表数据源丰富多样,支持表、视图、接口等一系列数据。这意味着用户可以根据实际需求,灵活选择不同类型的数据源,满足各种复杂业务场景的需求。无论是企业内部的数据库表,还是通过接口获取的外部数据,都能轻松整合到报表数据源中。
|
|
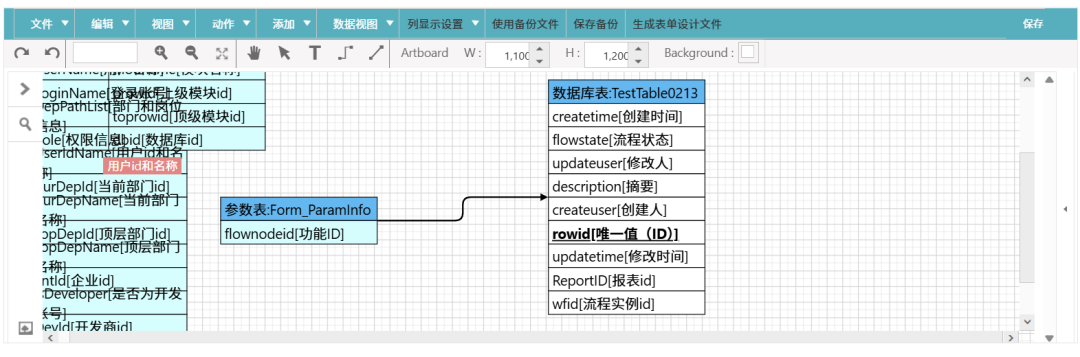
三、可视化数据关联
通过可视化的界面,用户可以方便地添加报表的数据源,并通过添加连线将不同数据进行关联。这种直观的操作方式,让用户无需深入了解底层的数据结构,即可轻松构建复杂的数据关系。只需简单地拖动和连接,就能实现数据的整合与交互。
|
|
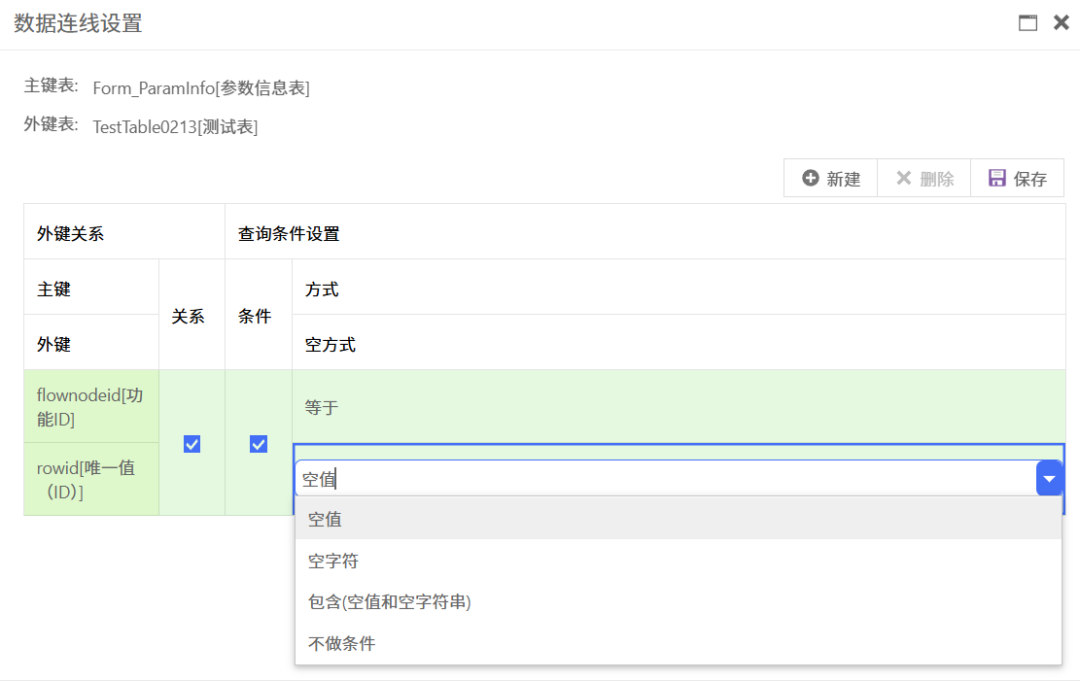
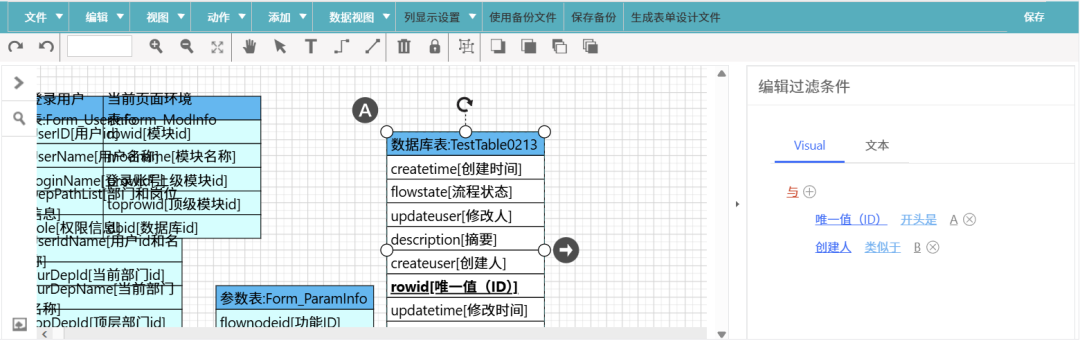
四、强大的数据筛选功能
勤研低代码开发平台不仅可以通过对连线的相关设置完成主子表数据筛选,还能让不同数据自身通过表达式添加不同的筛选条件。这为用户提供了极大的灵活性,可以根据特定的业务需求,精确地筛选出所需的数据。无论是基于特定的数值范围、文本匹配还是复杂的逻辑条件,都能轻松实现。
|
|
|
|
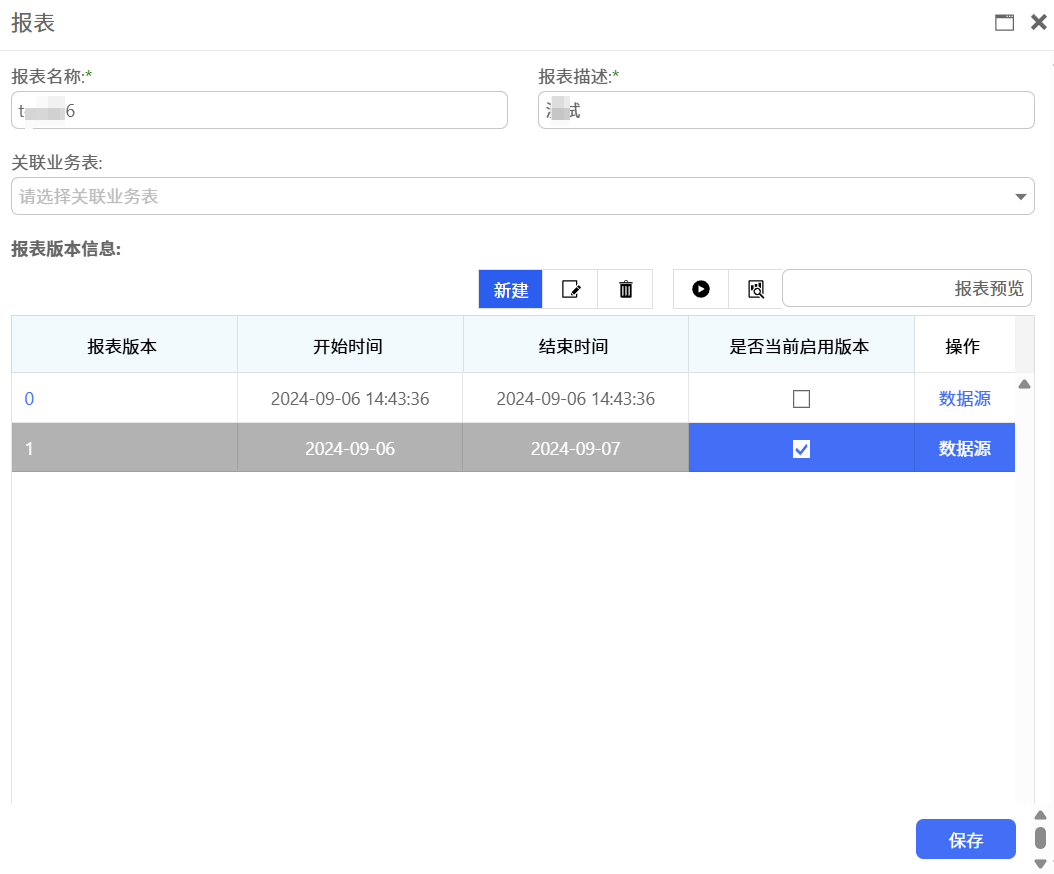
五、版本管理保障数据安全
值得一提的是,平台报表数据源支持版本管理。这一功能为数据的安全性和可追溯性提供了有力保障。用户可以随时查看和恢复不同版本的数据源,避免因误操作或数据变更而导致的问题。同时,版本管理也方便了团队协作,不同成员可以在不同版本上进行工作,互不干扰。
|
|
勤研低代码开发平台的报表数据源功能强大而便捷。它以快速创建报表、多样化的数据源支持、可视化的数据关联、强大的数据筛选功能和版本管理等功能,为用户提供了高效、可靠的报表数据源管理方案。无论是企业管理者、数据分析人员还是开发人员,都能在平台上轻松打造出满足自身需求的报表数据源,为后续的报表设计提供有力支持。

相关文章:

走进低代码报表开发(一):探秘报表数据源
在前文当中,我们对勤研低代码平台的流程设计功能进行了介绍。接下来,让我们一同深入了解在企业日常运营中另一个极为常见的报表功能。在当今数字化时代,高效的报表生成对于企业的决策至关重要。勤研低代码开发平台能够以卓越的性能和便捷的操…...
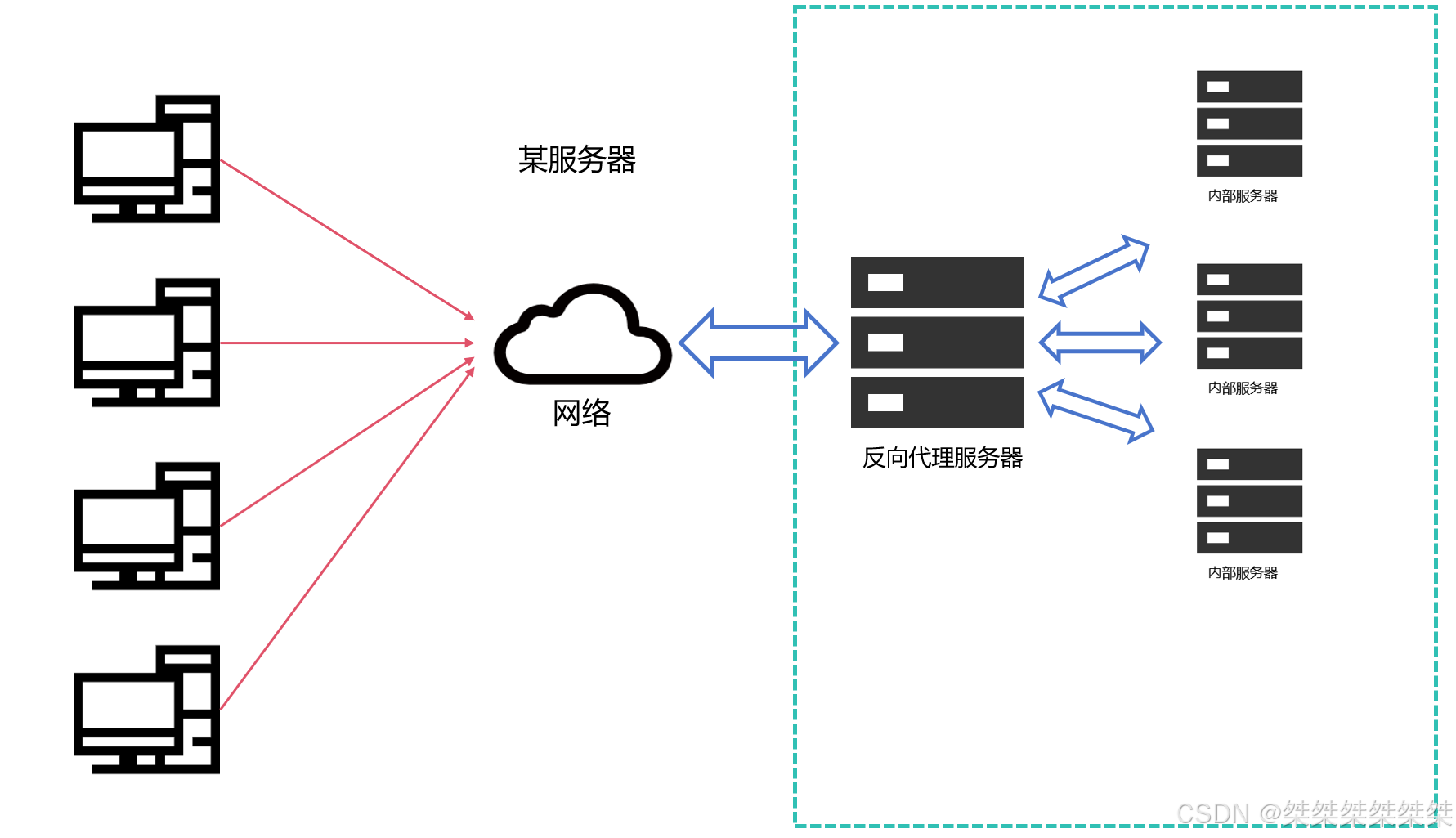
代理服务器及其原理
代理服务器的代理可以分为正向代理和反向代理,本篇将讲解这两种代理方式的原理,以及对应的功能特点和应用场景。最后还对比和 NAT 和代理服务器的区别。 目录 正向代理 工作原理 功能特点 应用场景 反向代理 基本原理 应用场景 NAT和代理服务器…...
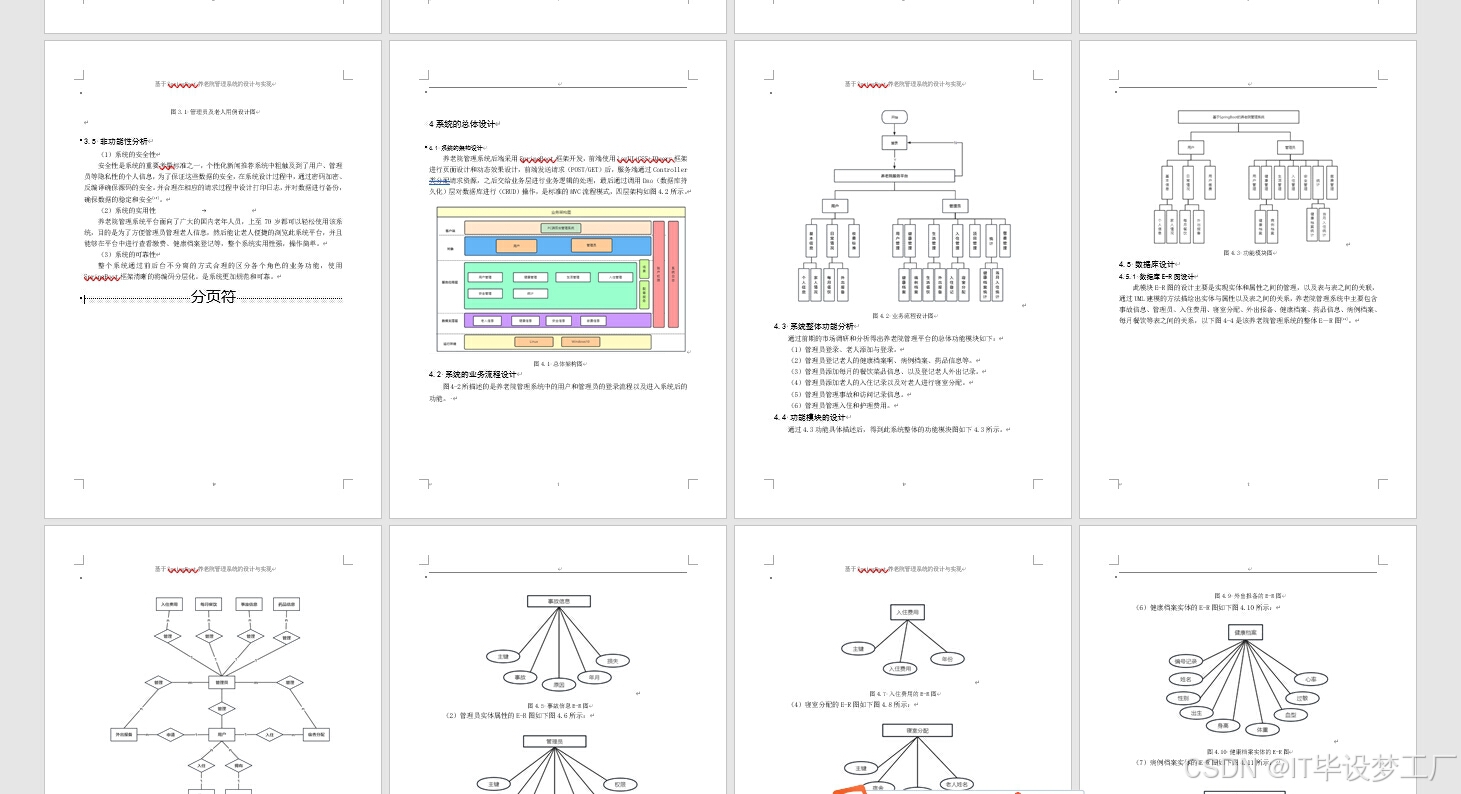
计算机毕业设计选题推荐-养老院管理系统-Java/Python项目实战
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

免费SSL证书正在逐渐被淘汰,证书部署自动化的发展趋势即将到来!
目录 背景解决方案。1.使用自签证书(浏览器报警、免费)2.更换支持自签自续的CA机构(免费)3.付费选择CA机构 免费SSL证书正在逐渐被淘汰,证书部署自动化的发展趋势即将到来免费的SSL证书有以下弊端1.有效期短࿱…...

openVX加速-基本概念和简单代码实现
OpenVX 是一个用于计算机视觉和图像处理的跨平台加速标准库,旨在提高在异构平台(如 CPU、GPU、DSP 等)上的执行效率。OpenVX 提供了一组优化的、可移植的 API,用于加速常见的视觉算法,使开发者能够在不同硬件平台上实现…...

网工内推 | 网络工程师,Base上海,HCIP/HCIE认证优先
01 利宏科技 🔷招聘岗位:网络工程师 🔷任职要求 1、有HCIE、HCIP证书 2、做过IDC机房网络建设 3、本科毕业 4、熟悉基本linux命令 5、熟悉山石、华为等防火墙 6、熟悉IPS、WAF等安全设备 7、做过同城灾备机房建设优先 🔷薪…...
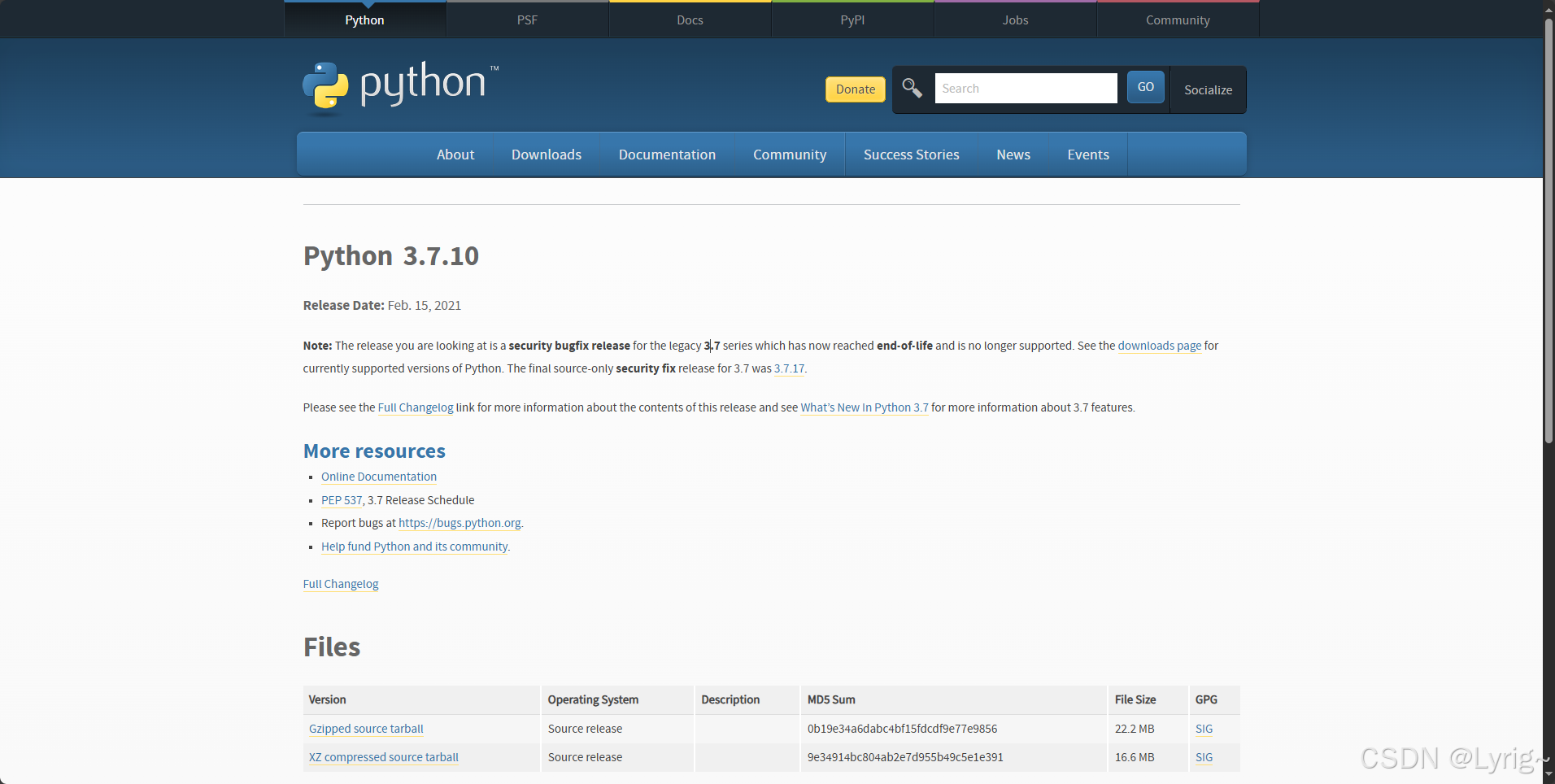
Windows10 如何配置python IDE
Windows10 如何配置python IDE 前言Python直接安装(快速上手)Step1.找到网址Step2.选择版本(非常重要)Step3. 安装过程Step4. python测试 Anaconda安装(推荐,集成了Spyder和Pycharm的安装)Step1…...

Machine Learning: A Probabilistic Perspective 机器学习:概率视角 PDF免费分享
下载链接在博客最底部!! 之前需要参考这本书,但是大多数博客都是收费才能下载本书。 在网上找了好久才找到免费的资源,浪费了不少时间,在此分享以节约大家的时间。 链接: https://pan.baidu.com/s/1erFsMcVR0A_xT4fx…...

信息学奥赛:青少年编程的高光舞台,通向未来科技的敲门砖
近年来,信息学奥林匹克竞赛(NOI,National Olympiad in Informatics)逐渐成为众多中学生学习编程、展示才华的热门赛事。这项被誉为“编程天才选拔赛”的竞赛,不仅考验学生的编程能力、算法思维,更是通向名校…...

Android - NDK:在Jni中打印Log信息
在Jni中打印Log信息 1、在配置CMakeLists.txt find_library( # Sets the name of the path variable.log-lib# Specifies the name of the NDK library that# you want CMake to locate.log)# Specifies libraries CMake should link to your target library. You # can link…...

websocket协议解说
WebSocket是一种在单个TCP连接上进行全双工通信的协议。 它为客户端和服务器之间提供了一个持久的连接,允许数据以帧的形式在客户端和服务器之间进行双向传输。 WebSocket协议特别适合需要实时通信的应用,如在线聊天、实时游戏、股票交易、实时监控系统…...

InternVL2-多模态模型原理-多模态模型和组合模型
好的,我会尽量用简单易懂的语言来解释InternVL和InternVL 1.5的工作原理。 InternVL和InternVL 1.5的工作原理 1. 模型结构 InternVL和InternVL 1.5都是由两个主要部分组成:一个视觉模型和一个语言模型。 视觉模型:负责处理图片信息。它的…...

大语言模型之ICL(上下文学习) - In-Context Learning Creates Task Vectors
本文译自 《In-Context Learning Creates Task Vectors》 —— 论文中的作者也在用LLaMA模型,笔者自我感觉拉近和世界顶级人才的距离,哈哈内容较长,如想看结论直接看 摘要、介绍与结论几个章节即可,看细节请看目录索引。经验风险最…...

出现错误消息“ sshd[xxxx]: error: no more session ”的原因是什么?
环境 • 红帽企业 Linux 6 • Red Hat Enterprise Linux 7 • openssh 问题 • SSH 选项的用途是什么MaxAuthTries,MaxSessions和MaxStartups? 解决 MaxAuthTries :指定每个连接允许的最大身份验证尝试次数。一旦失败次数达到此值的一半&…...

代码随想录训练营第29天|控制变量
134. 加油站 class Solution { public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int cur0, total0, start0;for(int i0; i<gas.size(); i){curgas[i]-cost[i];totalgas[i]-cost[i];if(cur<0){starti1;cur0;}}if(start>gas…...
毕业论文选题难?5招帮你轻松搞定选题!
AIPaperGPT,论文写作神器~ https://www.aipapergpt.com/ 你是不是已经为毕业论文的选题愁得头发都要掉光了?每次打开文档,都觉得什么都想写,又好像什么都写不了。选题看起来很简单,但真正开始动手的时候,…...

[QT]记事本项目(信号槽,QT基础控件,QT文件操作,QT关键类,对话框,事件)
一.UI界面搭建 (ui界面使用,界面布局,各控件介绍,界面大小调整) 二.信号槽机制实现文件的打开,保存,退出 (信号槽,QFile文件类,QTextStream类,QFileDialog文件对话框࿰…...

redis基本数据结构-hash
这里写自定义目录标题 1. redis的数据结构hash1.1 Hash 数据结构的特点1.2 常见命令1.3 适用示例 2. 常见业务场景2.1 用户信息存储2.1.1 场景2.1.2 优势2.1.3 解决方案2.1.4 代码实现 2.2 购物车管理2.2.1 背景2.2.2 优势2.2.3 解决方案2.2.4 代码实现 3. 注意事项:…...

21. 什么是MyBatis中的N+1问题?如何解决?
N1 问题是指在进行一对多查询时,应用程序首先执行一条查询语句获取结果集(即 1),然后针对每一条结果,再执行 N 条额外的查询语句以获取关联数据。这个问题通常出现在 ORM 框架(如 MyBatis 或 Hibernate&…...

天空卫士项目荣获“2024 IDC 中国20大杰出安全项目 ”奖项 ,实力见证安全守护
9月11日, IDC在上海圆满举办安全风险管控峰会,并现场官宣“2024 IDC中国20大杰出安全项目(CSO20) ”和“2024 IDC中国 CSO名人堂 (十大人物) ” 奖项名单。联通软研院申报的联通邮件系统安全合规建设项目被评为“2024 IDC中国20大杰出安全项目(CSO20) ”…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...