【数据结构】排序算法系列——希尔排序(附源码+图解)
希尔排序
算法思想
希尔排序(Shell Sort)是一种改进的插入排序算法,希尔排序的创造者Donald Shell想出了这个极具创造力的改进。其时间复杂度取决于步长序列(gap)的选择。我们在插入排序中,会发现是对整体数据直接进行了统一的插入排序,每个数据之间的间隙是1,这里的1指的就是步长序列gap。在希尔排序中,我们会将整体数据一分为多份,进行散布式的插入排序,这时候每一个子序列之间的间隙就是gap——那么事实上我们也可以将插入排序就看成是gap=1的希尔排序。
我们来具体分析希尔排序的算法步骤:
- 将待排序序列分为若干个序列,每个序列的间距n(gap)需要相同
- 将这些子序列分别进行插入排序
- 不断减小这个间距
那么我们减小这个间距的目的是什么呢?
当gap > 1时我们可以称为预排序,目的是让数组更接近于有序。当gap = 1时,数组已经接近有序的了,就整体而言,最后一次整体的插入排序就可以大大提高效率——我们从插入排序的时间复杂度分析也可以看出,越接近有序,插入排序的效率就越高,从而可以达到优化的效果。
图解

可以看到每次减小gap的规律是将原先的gap/2,但事实上这只是其中一种处理方法,并不说明这是最优解。
C语言代码分析
//与插入排序类似,只是插入排序的间隔是1,而希尔排序的间隔是gap//第一种思想:依次排序
//排完一组后,再排下一组
void ShellSort1(int arr[], int n)
{int gap = 3;//任意一个想要的间隔for (int j; j < gap; j++){for (int i = gap; i < n; i += gap){int end = i - gap;int tmp = arr[end + gap];while (end >= 0){if (tmp >= arr[end]){arr[end + gap] = tmp;end -= gap;}else{break;}}arr[end + gap] = tmp;}}}//第二种思想:多组并排
void ShellSort2(int arr[], int n)
{int gap = 3;//任意一个想要的间隔for (int i = gap; i < n-gap; i ++){int end = i;int tmp = arr[i + gap];while (end >= 0){if (tmp >= arr[end]){arr[end + gap] = tmp;end -= gap;}else{break;}}arr[end + gap] = tmp;}
}//gap越大,跳得越快,但一次排下来最无序
//gap越小,跳得越慢,但一次排下来更有序
注意
希尔排序实际上是个相当复杂的排序算法,这主要是跟它的步长序列gap到底该如何取、后续应该减小有关。这其中涉及到很多的数学分析以及数学公式,我们可以参考严蔚敏老师的解读:

以及殷人昆老师:

所以,本篇文章仅对其基本的算法思想和代码编写进行解析,如有兴趣深究希尔排序,各位读者们可以自行上网搜索有关知识~
时间复杂度
一般情况下,希尔排序的时间复杂度可以表示为:
- 最好情况(已排序的情况):O(n log n)
- 平均情况:取决于步长序列的选择,通常为**O(n1.3)-O(n2)**之间。
- 最坏情况:O(n2)
希尔排序通过逐步减少步长来实现排序,初始的大步长使得数组元素可以较快地达到部分有序状态,最终通过小步长的插入排序完成排序。所以时间复杂度的具体分析也就取决于步长序列。
这里针对平均情况,我们进行一下简单的具体分析:
希尔排序的平均情况时间复杂度是比较复杂的。在实际应用中,常见的步长序列如希尔建议的序列(1, 3, 7, …, 2^k-1)或者Hibbard序列(1, 3, 7, 15, …, 2k-1)等,它们的时间复杂度通常就在**O(n1.3)-O(n2)**之间,这是经过数学算出来的结果。这些序列被设计为逐渐减小,从而在较早阶段快速减少逆序对的数量,然后在最后阶段完成排序。
总体来说,希尔排序的性能高度依赖于步长序列的选择。良好的步长序列可以显著改善排序的效率,使得平均情况下的时间复杂度能够在O(n^1.3)左右,而不好的选择则可能导致接近最坏情况的性能。
稳定性
鉴于希尔排序会改变前后元素的相对位置,所以:不稳定
相关文章:

【数据结构】排序算法系列——希尔排序(附源码+图解)
希尔排序 算法思想 希尔排序(Shell Sort)是一种改进的插入排序算法,希尔排序的创造者Donald Shell想出了这个极具创造力的改进。其时间复杂度取决于步长序列(gap)的选择。我们在插入排序中,会发现是对整体…...

c++(继承、模板进阶)
一、模板进阶 1、非类型模板参数 模板参数分类类型形参与非类型形参。 类型形参即:出现在模板参数列表中,跟在class或者typename之类的参数类型名称。 非类型形参,就是用一个常量作为类(函数)模板的一个参数,在类(函数)模板中…...

【机器学习】从零开始理解深度学习——揭开神经网络的神秘面纱
1. 引言 随着技术的飞速发展,人工智能(AI)已从学术研究的实验室走向现实应用的舞台,成为推动现代社会变革的核心动力之一。而在这一进程中,深度学习(Deep Learning)因其在大规模数据处理和复杂问题求解中的卓越表现,迅速崛起为人工智能的最前沿技术。深度学习的核心是…...
WebLogic 笔记汇总
WebLogic 笔记汇总 一、weblogic安装 1、创建用户和用户组 groupadd weblogicuseradd -g weblogic weblogic # 添加用户,并用-g参数来制定 web用户组passwd weblogic # passwd命令修改密码# 在文件末尾增加以下内容 cat >>/etc/security/limits.conf<<EOF web…...

leetcode:2710. 移除字符串中的尾随零(python3解法)
难度:简单 给你一个用字符串表示的正整数 num ,请你以字符串形式返回不含尾随零的整数 num 。 示例 1: 输入:num "51230100" 输出:"512301" 解释:整数 "51230100" 有 2 个尾…...

Python GUI入门详解-学习篇
一、简介 GUI就是图形用户界面的意思,在Python中使用PyQt可以快速搭建自己的应用,自己的程序看上去就会更加高大上。 有时候使用 python 做自动化运维操作,开发一个简单的应用程序非常方便。程序写好,每次都要通过命令行运行 pyt…...

QT5实现https的post请求(QNetworkAccessManager、QNetworkRequest和QNetworkReply)
QT5实现https的post请求 前言一、一定要有sslErrors处理1、问题经过2、代码示例 二、要利用抓包工具1、问题经过2、wireshark的使用3、利用wireshark查看服务器地址4、利用wireshark查看自己构建的请求报文 三、返回数据只能读一次1、问题描述2、部分代码 总结 前言 QNetworkA…...

vscode 使用git bash,路径分隔符缺少问题
window使用bash --login -i 使用bash时候,在系统自带的terminal里面进入,测试conda可以正常输出,但是在vscode里面输入conda发现有问题 bash: C:\Users\marswennaconda3\Scripts: No such file or directory实际路径应该要为 C:\Users\mars…...
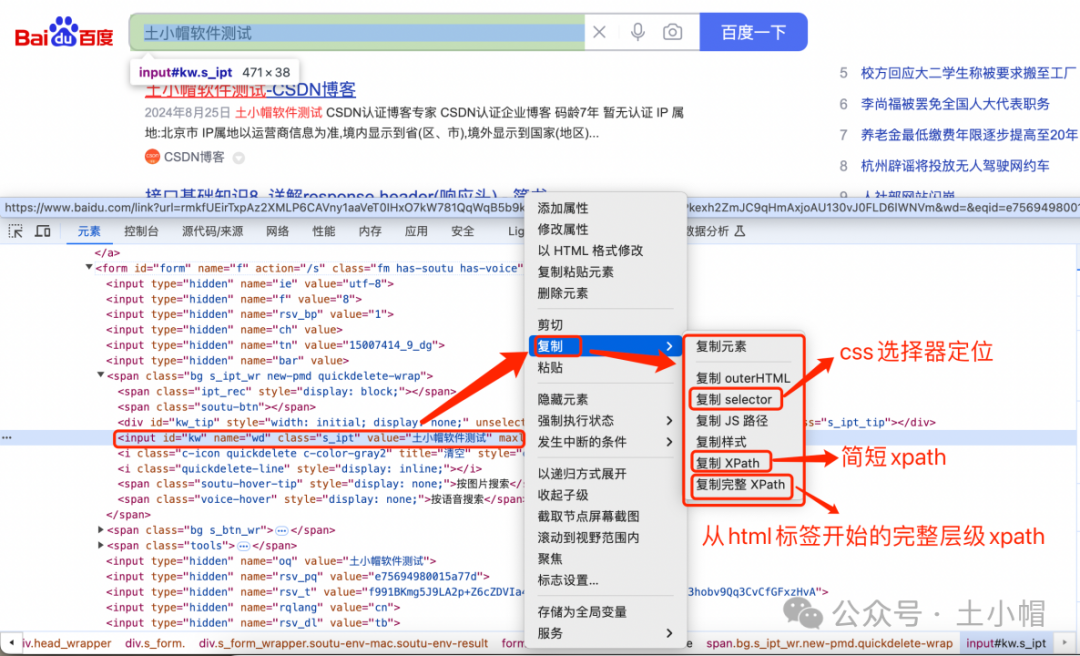
F12抓包10:UI自动化 - Elements(元素)定位页面元素
课程大纲 1、前端基础 1.1 元素 元素是构成HTML文档的基本组成部分之一,定义了文档的结构和内容,比如段落、标题、链接等。 元素大致分为3种:基本结构、自闭合元素(self-closing element)、嵌套元素。 1、基本结构&…...

android 删除系统原有的debug.keystore,系统运行的时候,重新生成新的debug.keystore,来完成App的运行。
1、先上一个图:这个是keystore无效的原因 之前在安装这个旧版本android studio的时候呢,安装过一版最新的android studio,然后通过模拟器跑过测试的demo。 2、运行旧的项目到模拟器的时候,就报错了: Execution failed…...

SQL入门题
作者SQL入门小白,此栏仅是记录一些解题过程 1、题目 用户访问表users,记录了用户id(usr_id)和访问日期(log_date),求出连续3天以上访问的用户id。 2、解答过程 2.1数据准备 通过navicat创建数据…...

Python实战:实战练习案例汇总
Python实战:实战练习案例汇总 **Python世界系列****Python实践系列****Python语音处理系列** 本文逆序更新,汇总实践练习案例。 Python世界系列 Python世界:力扣题43大数相乘算法实践Python世界:求解满足某完全平方关系的整数实…...

zabbix之钉钉告警
钉钉告警设置 我们可以将同一个运維组的人员加入到同一个钉钉工作群中,当有异常出现后,Zabbix 将告警信息发送到钉钉的群里面,此时,群内所有的运维人员都能在第一时间看到这则告警详细。 Zabbix 监控系统默认没有开箱即用…...

《OpenCV计算机视觉》—— 对图片进行旋转的两种方法
文章目录 一、用numpy库中的方法对图片进行旋转二、用OpenCV库中的方法对图片进行旋转 一、用numpy库中的方法对图片进行旋转 numpy库中的 np.rot90 函数方法可以对图片进行旋转 代码实现如下: import cv2 import numpy as np# 读取图片 img cv2.imread(wechat.jp…...
)
Python 错误 ValueError 解析,实际错误实例详解 (一)
文章目录 前言Python 中错误 ValueError: No JSON object Could Be Decoded在 Python 中解码 JSON 对象将 JSON 字符串解码为 Python 对象将 Python 对象编码为 JSON 字符串Python 中错误 ValueError: Unsupported Pickle Protocol: 3Python 中的 Pickling 和 UnpicklingPython…...

[java][git]上传本地代码及更新代码到GitHub教程
上传本地代码及更新代码到GitHub教程 上传本地代码 第一步:去github上创建自己的Repository,创建页面如下图所示: 红框为新建的仓库的https地址 第二步: echo "# Test" >> README.md 第三步:建立g…...

react antd table expandable defaultExpandAllRows 不生效问题
原因:defaultExpandAllRows只会在第一次渲染时触发 解决方案:渲染前判断table 的datasource 数据是否已准备好 {pageList.length > 0 ? (<TablerowSelection{rowSelection}columns{columns}dataSource{pageList}style{{ marginTop: 24 }}pagina…...

什么是领域驱动设计?
什么是领域驱动设计? 领域驱动设计(Domain-Driven Design,简称DDD)是一种面向对象的软件开发方法,它强调将软件系统的设计和实现过程与业务领域紧密结合,通过深入理解和建模业务领域,从而实现高…...

信息安全工程师(1)计算机网络分类
一、按分布范围分类 广域网(WAN): 定义:广域网的任务是提供长距离通信,运送主机所发送的数据。其覆盖范围通常是直径为几十千米到几千千米的区域,因此也被称为远程网。特点:连接广域网的各个结点…...

利士策分享,探索无界:心灵之旅,发现未知精彩
利士策分享,探索无界:心灵之旅,发现未知精彩 梦想的种子,在心田生根发芽 正如每一颗种子都蕴含着生命的奥秘,每个人心中那颗探索的种子,也藏着对未知世界的渴望与追求。它告诉我们,成长不仅仅…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
