【人工智能】人工智能领域中的线性回归算法原理、应用场景及代码示例。
🏆🏆欢迎大家来到我们的天空🏆🏆
🏆🏆如果文章内容对您有所触动,别忘了点赞、关注,收藏!
🏆 作者简介:我们的天空
🏆《头衔》:阿里云开发者社区专家博主,CSDN人工智能领域新星创作者。
🏆《博客》:人工智能,深度学习,机器学习,python,自然语言处理,AIGC等分享。所属的专栏:TensorFlow项目开发实战,人工智能技术
🏆🏆主页:我们的天空
一、人工智能领域中的线性回归算法原理
线性回归是人工智能和机器学习中最基础且广泛应用的算法之一。它的核心思想是找到自变量(X)和因变量(Y)之间的最佳线性关系,即找到一个线性方程(或模型)来预测目标值。这个线性方程通常表示为 Y = wX + b,其中 Y 是预测值,X 是自变量(可以是多维的),w 是权重(系数),b 是偏置项(截距)。线性回归的目标是通过训练数据(已知的自变量和因变量对)来找到最佳的 w 和 b 值,使得预测值与实际值之间的误差(通常是均方误差)最小。
具体来说,线性回归模型可以表示为:
𝑦=𝛽0+𝛽1𝑥1+𝛽2𝑥2+...+𝛽𝑛𝑥𝑛+𝜖y=β0+β1x1+β2x2+...+βnxn+ϵ
其中:
- 𝑦y 是因变量。
- 𝑥𝑖xi 是自变量。
- 𝛽0,𝛽1,...,𝛽𝑛β0,β1,...,βn 是待估计的参数。
- 𝜖ϵ 是误差项,表示模型无法解释的随机噪声。
线性回归通过最小化预测值与真实值之间的平方差来估计这些参数,即:
𝑅𝑆𝑆=∑𝑖=1𝑛(𝑦𝑖−(𝛽0+𝛽1𝑥𝑖1+𝛽2𝑥𝑖2+...+𝛽𝑛𝑥𝑖𝑛))2RSS=∑i=1n(yi−(β0+β1xi1+β2xi2+...+βnxin))2
二、优点
- 简单易懂:线性回归模型直观易懂,便于解释。
- 计算效率高:线性回归的计算相对简单,特别是对于大规模数据集,可以通过矩阵运算来加速计算。
- 易于实现:大多数编程语言和机器学习库都提供了线性回归的实现,便于开发者快速上手。
- 结果可解释性强:通过线性回归的系数,可以清晰地了解自变量对因变量的影响程度和方向。
三、缺点
- 对非线性关系拟合能力差:如果数据中存在复杂的非线性关系,线性回归的拟合效果将会较差。
- 对异常值敏感:线性回归模型对异常值较为敏感,异常值可能会对模型的预测结果产生较大影响。
- 特征选择:线性回归模型的性能很大程度上依赖于特征的选择和预处理,不恰当的特征选择可能会导致模型性能下降。
四、应用场景
- 房价预测:根据房屋的面积、位置、房间数等特征来预测房价。
- 销售预测:根据历史销售数据、广告投入、促销活动等来预测未来的销售量。
- 经济预测:根据宏观经济指标(如GDP、失业率等)来预测未来的经济走势。
- 生物信息学:在生物信息学中,线性回归可以用于基因表达数据的分析,以识别与特定表型相关的基因。
- 股票市场: 通过分析市场指数、公司财报等数据来预测股票价格的变化趋势。
- 医疗健康: 通过患者的年龄、体重等特征预测疾病的发生概率。
五、代码示例
这里我们使用 Python 和 Scikit-Learn 库来演示如何实现一个简单的线性回归模型。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score# 生成模拟数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建线性回归模型
lin_reg = LinearRegression()# 训练模型
lin_reg.fit(X_train, y_train)# 预测
y_pred = lin_reg.predict(X_test)# 评估模型
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)print("Mean squared error: %.2f" % mse)
print("Coefficient of determination (R^2): %.2f" % r2)# 绘制结果
plt.scatter(X_test, y_test, color='black')
plt.plot(X_test, y_pred, color='blue', linewidth=3)plt.xticks(())
plt.yticks(())plt.show()六、代码解释
- 数据生成: 生成了一个简单的线性数据集,其中包含了一些随机噪声。
- 数据划分: 将数据集划分为训练集和测试集。
- 模型训练: 使用训练集数据训练线性回归模型。
- 预测: 使用测试集数据进行预测。
- 评估: 计算预测结果与真实值之间的均方误差(MSE)和决定系数(R²)。
- 绘图: 绘制真实的测试数据点以及模型的预测线。
通过上述代码示例,我们可以看到线性回归模型如何被用来拟合数据,并通过图形直观展示模型的效果。注意,在实际应用中,你需要使用更复杂和真实的数据集来训练模型。
推荐阅读:
1.【AIGC】Transformer模型:Postion Embedding概述、应用场景和实现方式的详细介绍。
2.【AIGC】Whisper语音识别模型概述,应用场景和具体实例及如何本地搭建Whisper语音识别模型?
3.【人工智能】TensorFlow lite介绍、应用场景以及项目实践:使用TensorFlow Lite进行数字分类
4.【人工智能】项目案例分析:使用LSTM生成图书脚本
5.【人工智能】案例分析和项目实践:使用高斯过程回归预测股票价格
相关文章:

【人工智能】人工智能领域中的线性回归算法原理、应用场景及代码示例。
🏆🏆欢迎大家来到我们的天空🏆🏆 🏆🏆如果文章内容对您有所触动,别忘了点赞、关注,收藏! 🏆 作者简介:我们的天空 🏆《头衔》&#x…...

day18JS-微任务、宏任务和node.js
1. 代码的执行流程 代码的执行流程分为同步与异步。 2. 什么样子的是宏任务? 1. setTimeout 和 setInterval 定时器: 没有写时间(传参的),代表下一帧执行,如果没有其他任务1ms后执行。 // 没有写时间(传参的),代表下…...

Mega Stamp Bundle 地形合集捆绑包峡谷沙丘山脉
终极套装,满足所有地形雕刻需求! 自2015年Gaia发布以来,我们团队就发明了印章技术,欢迎来到Mega Stamp Bundle! 本套装包含14个印章包,单次购买即可享受大幅折扣,共获得140个专业设计的印章。 这些印章可与Unity Terrain Tools、Gaia以及任何使用印章高度图图像的工具…...
基于SpringBoot+Vue+MySQL的明星周边产品销售网站系统
系统展示 用户前台界面 管理员后台界面 系统背景 在当今数字化消费时代,粉丝经济蓬勃发展,明星周边产品作为连接明星与粉丝的重要纽带,市场需求日益增长。为了满足广大粉丝对明星周边产品的热情追求,并提升购物体验,我…...

websocket 和sip 在协议层面有哪些区别,为什么要各自这样设置协议
WebSocket 和 SIP(Session Initiation Protocol)在协议层面有显著区别,因为它们各自的设计目标和用途不同。让我们从协议的定义、工作方式和用途来讨论这些区别: 1. 协议定义与用途 WebSocket: WebSocket 是一种通信协议,旨在通过单个 TCP 连接实现全双工通信。它用于在客…...

Miracast/WifiDisplay开发相关的深入调研分析-android投屏实战开发
Miracast/WifiDisplay概念介绍 Miracast Miracast是由Wi-Fi联盟于2012年所制定,以Wi-Fi直连(Wi-Fi Direct)为基础的无线显示标准。支持此标准的消费性电子产品(又称3C设备)可透过无线方式分享视频画面,例如…...
linux入门到实操-4 linux系统网络配置、连接测试、网络连接模式、修改静态IP、配置主机名
教程来源:B站视频BV1WY4y1H7d3 3天搞定Linux,1天搞定Shell,清华学神带你通关_哔哩哔哩_bilibili 整理汇总的课程内容笔记和课程资料(包含课程同版本linux系统文件等内容),供大家学习交流下载:…...
【kubernetes】Ingress和Ingress-Controller介绍,高可用应用案例
一,Ingress介绍 Ingress是k8s中一种重要的资源对象,它主要用于定义从集群外部到集群内部服务的HTTP(S)路由规则。用于管理代理 Ingress-Controller的配置文件。 kubectl explain ingress二,Ingress-Controller介绍 Ingress Controller 是 …...
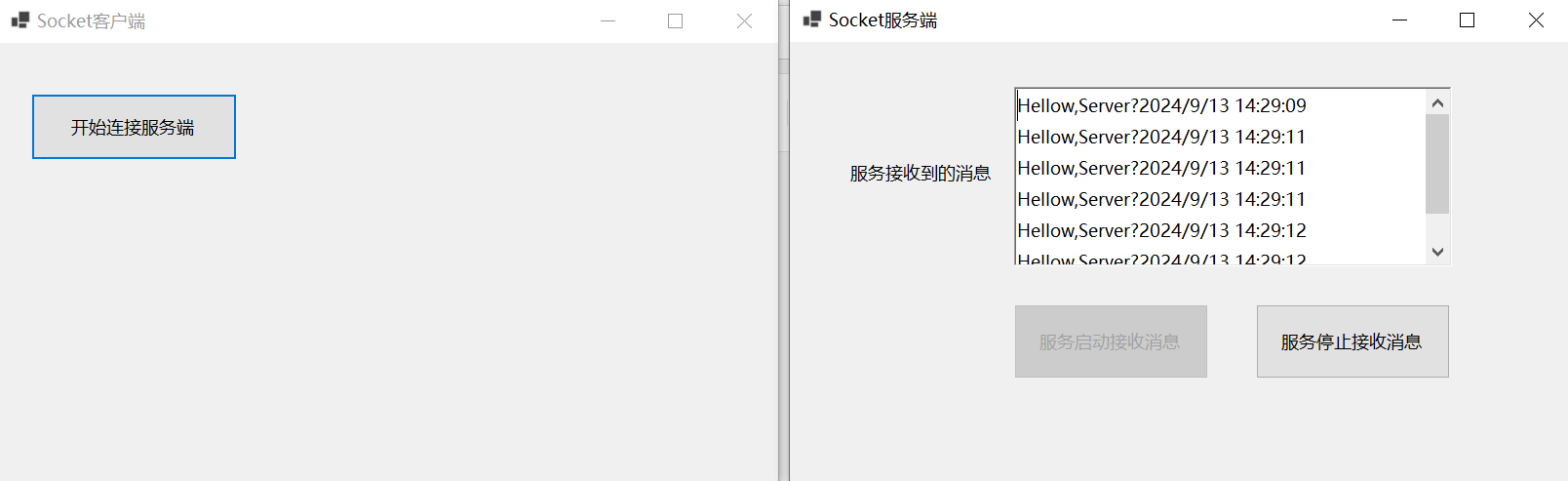
C# 使用Socket通信,新建WinForm服务端、客户端程序
一、新建WinForm Socket服务端程序 注:rtbReceviceMsg为RichTextBox控件 服务端程序、界面 服务端代码 public partial class Form1 : Form {public Form1(){InitializeComponent();}public virtual void TriggerOnUpdateUI(string message){if (this.InvokeRequir…...
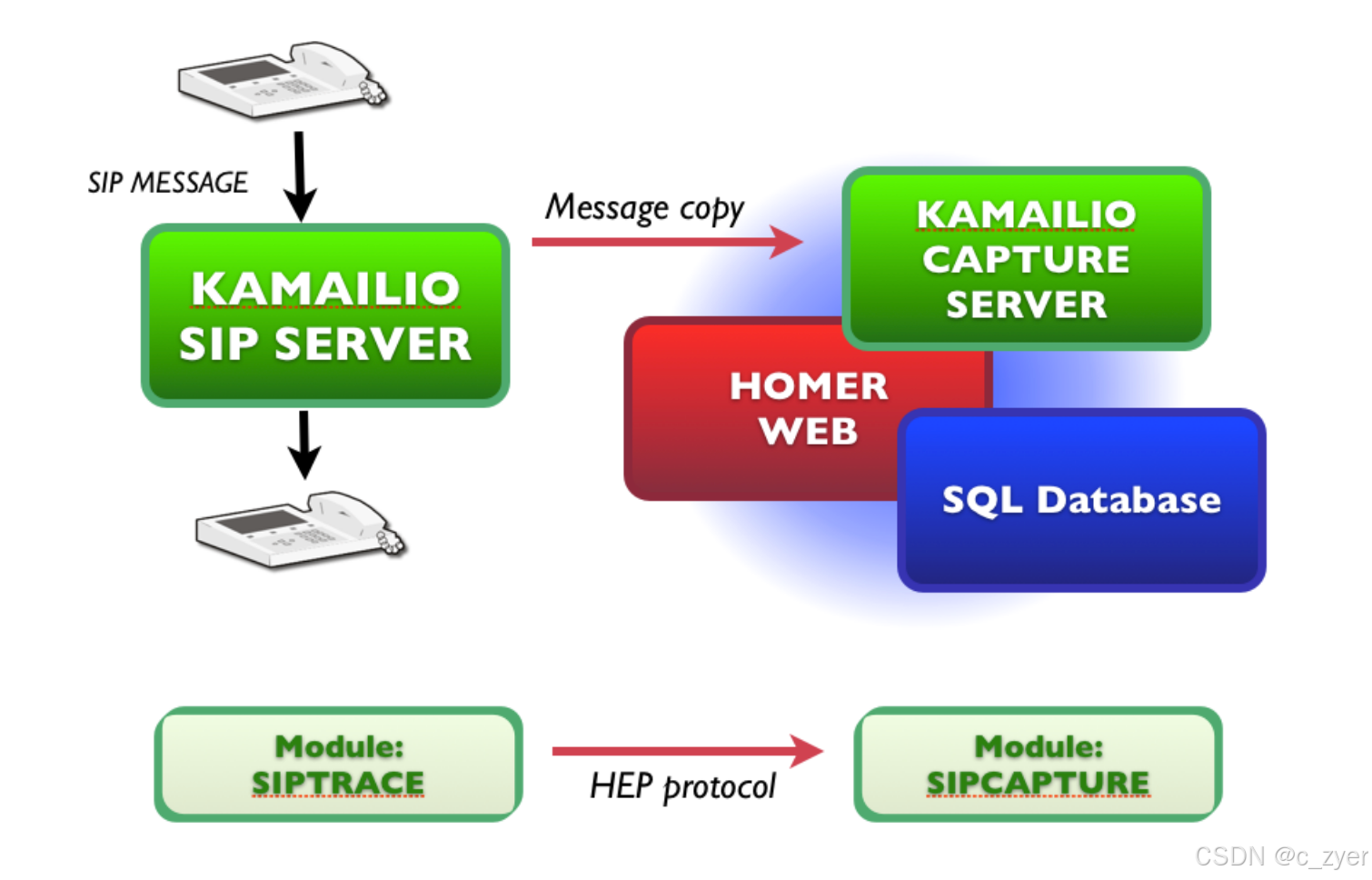
Kamailio-基于Homer与heplify的SIP信令监控-2
接上篇,我们已经顺利地完成了服务的安装,下面就来看看如何配置并启动。 跟着我,你将学会: 下载并安装 踩坑:按照官方步骤来,可是网络条件不允许 获取YUM源下载RPM包手动解压安装避坑 配置并启动…...
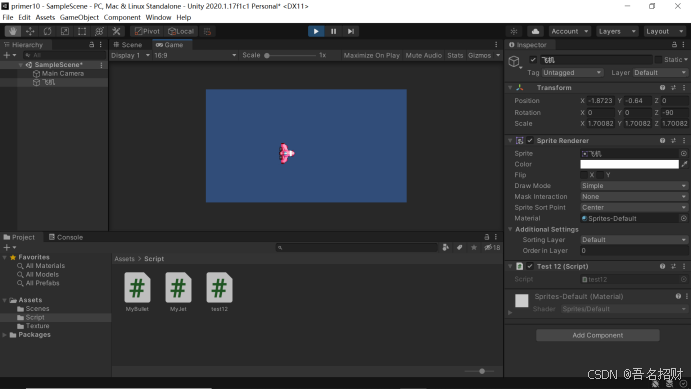
unity3d入门教程四
unity3d入门教程四 10.1坐标与旋转10.2物体的运动10.3(练习)掉头飞行11.1向量11.2向量间运算11.3向量夹角11.4物体的指向11.5(练习)飞向目标12.1屏幕坐标12.2屏幕的边界 10.1坐标与旋转 比如,节点的坐标用 Vector3 类型…...

无人机飞控的原理!!!
一、传感器系统 陀螺仪:用于检测无人机的角速度和角度,帮助确定无人机的姿态。 加速度计:用于检测无人机的加速度和倾斜角度,进一步辅助姿态判断。 磁力计(或罗盘):用于检测无人机的方向&…...
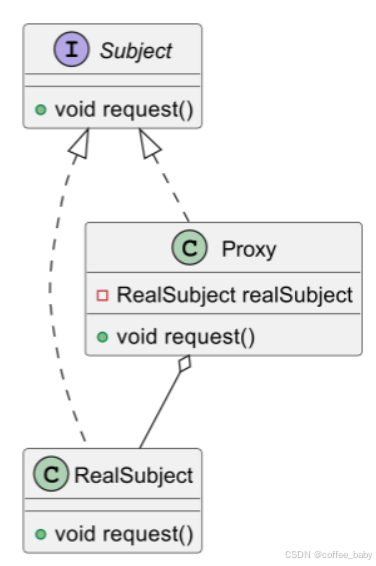
深入解析代理模式:静态代理、JDK 动态代理和 CGLIB 的全方位对比!
代理模式(Proxy Pattern)是一种结构型设计模式,它提供了对象的替身,即代理对象来控制对实际对象的访问。通过代理对象,可以在不修改目标对象的情况下,扩展或控制其功能。例如,代理模式可以用于延…...

51单片机快速入门之独立按键
51单片机快速入门之独立按键 这里我们需要用上一个仿真软件,只因不想硬件焊接:PROTEUS DESIGN SUITE PROTEUS DESIGN SUITE: PROTEUS DESIGN SUITE是一款由LabCenter Electronics开发的电子设计自动化(EDA)软件,广泛应用于电气工程和电子工…...

设计模式之工厂模式(通俗易懂--代码辅助理解【Java版】)
文章目录 设计模式概述1、工厂模式概述1)特点:2)主要角色:3)工作流程:4)优点5)缺点6)适用场景 2、简单工厂模式(静态工厂模式)1) 在简单工厂模式中,有三个主要…...

速盾:高防 cdn 分布式防御攻击?
在当今数字化时代,网络安全问题日益凸显,各种网络攻击手段层出不穷。为了保护企业和个人的网络资产安全,高防 CDN(Content Delivery Network,内容分发网络)成为了一种重要的防御手段。其中,分布…...
Unity3D类似于桌面精灵的功能实现
前言: 由于最近在做游戏魔改,很多功能在游戏里面没法实现(没错,说的就是排行榜),所以准备用Unity3D开发一个类似于桌面精灵的功能部件,实现效果如下: PS:有需要定制的老…...

Audio Over IP的PTP时钟初探
Audio Over IP的PTP时钟初探 这几天参加省局举办的技术能手比赛,第一次接触并了解AOIP(Audio Over IP)相关的理论和实践相关的知识。其中AoIP的时钟同步采用的是IEEE 1588 标准的PTP(Precision Time Protocol)基于网络…...
)
【加密社】深入理解TON智能合约 (FunC语法)
king: 摘要:在TON(TheOpenNetwork)区块链平台中,智能合约扮演着举足轻重的角色。本文将通过分析一段TON智能合约代码 带领读者学习dict(字典)和list(列表)在FunC语言中的用法&#x…...

笔试强训day11
游游的水果大礼包 #include <iostream> #define int long longusing namespace std; int n, m, a, b;signed main() {cin>>n>>m>>a>>b;int ret 0;for(int x 0; x < min(n / 2, m); x) // 枚举 1 号礼包的个数{int y min(n - x * 2, (m - …...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
