2024年华为9月4日秋招笔试真题题解
2024年华为0904秋招笔试真题
- 二叉树消消乐
- 好友推荐系统
- 维修工
- 力扣上类似的题--K站中转内最便宜的航班
二叉树消消乐
题目描述
给定原始二叉树和参照二叉树(输入的二叉树均为满二叉树,二叉树节点的值范围为[1,1000],二叉树的深度不超过1000),现对原始二叉树和参照二叉树中相同层级目值相同的节点进行消除、消除规则为原始叉树和参照二叉树中存在多个值相同的节点只能消除等数量的、消除后的节点变为无效节点,请按节点值出现频率从高到低输出消除后原始二叉树中有效节点的值(如果原始二叉树消除后没有有效节点返回0)。
输入描述
原始二叉树中的节点个数
原始二叉树
参照二叉树中的节点个数
参照二叉树
输出描述
原始二叉树中有效节点的值,按出现频率从高到低排序(相同频率的值按大小排序),相同频率的值按降序排列。
用例输入
7
1 3 3 3 4 5 6
3
2 3 4
用例输出
36541
样例1解释:
原始二叉树A消除参照二叉树B中的重复元素后,有效节点剩余2个3,1个6,1个5,1个4,1个1,3出现的频率2,6、5、4、1出现的频率为1,按值从大到小排序、所以排序结果为36541。
求解思路
注意审题,题目明确指出这是一个满二叉树,因此我们不需要真的去构建一个二叉树,只需要利用满二叉树的性质去进行模拟求解就行。
需要注意的是,华为的命题人在写题面时候不够严谨,题面说二叉树的深度不超过1000,这显然是不现实的,毕竟这是满二叉树,如果深度达到几十上百的话,二叉树的节点数直接2的几百次方,显然这么大的数据哪怕O(n)的时间复杂度也过不了。因此只需要按照节点数为1e5的规模来设计算法即可。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 100001;
int n, m;
int origin[maxn], refer[maxn];
vector<int>sum(maxn, 0);void dfs(int depth) {int start = pow(2, depth - 1), end = start + pow(2, depth - 1);if(start > n || start > m) return;map<int, int>mp1, mp2;for(int i = start; i < end; i++) {mp1[origin[i]]++;mp2[refer[i]]++;}for(auto i : mp1) {if(mp2[i.first] > i.second) sum[i.first] -= i.second;else sum[i.first] -= mp2[i.first];// cout << i.first << " " << sum[i.first] << endl;}dfs(depth + 1);
}bool cmp(pair<int, int>a, pair<int, int> b) {if(a.second != b.second) return a.second > b.second;return a.first > b.first;
}int main() {scanf("%d", &n);for(int i = 1; i <= n; i++) {scanf("%d", &origin[i]);sum[origin[i]]++;}scanf("%d", &m);for(int i = 1; i <= m; i++) scanf("%d", &refer[i]);dfs(1);// for(int i = 1; i <= n; i++) cout << sum[origin[i]] << " ";// cout << endl;vector<pair<int, int>>v;set<int>s;for(int i = 1; i <= n; i++) s.insert(origin[i]);for(auto i : s) v.push_back(make_pair(i, sum[i]));// for(auto i : s) cout << i << " " << sum[i] << " " << endl;sort(v.begin(), v.end(), cmp);bool flag = false;for(auto i : v) {if(i.second != 0) {flag = true;printf("%d", i.first);} else break;}if(!flag) printf("0");return 0;
}
/*
15
5 8 8 8 7 7 7 6 6 9 9 7 7 5 6
7
5 6 6 7 7 8 8
*/
好友推荐系统
题目描述
你正在为一个社交网络平台开发好友推荐功能。
平台上有N个用户(每个用户使用1到N的整数编号),同时系统中维护了用户之间的好友关系。
为了推荐新朋友,平台决定采用“共同好友数量"作为衡量两个用户之间相似度的标准。
系统根据输入用户编号K,输出与此用户K相似度最高的前L个用户ID来推荐给用户K。
相似度定义:两个用户非好友,两个用户的相似度为拥有的共同好友数(例如用户A和用户B,只有共同好友C和D,相似度=2)
输入描述
第一行包含四个整数 N,M 、K和L,分别表示用户的数量(N),好友记录条数(M)、查询的用户编号(K)和推荐的好友数量(L)。接下来 M 行,每行包含两个整数编号X和Y,表示编号为X和Y用户是好友。
-
输入格式都是标准的,无需考虑输出异常场景(不会包含用户和自己是好友的输入,例如11)
-
用户数不超过1024,用户编码最大1024
-
好友记录数不超过10240
输出描述
根据输入K和L,输出和用户K相似度最高的L个用户编码。
-
输出相似度最高的前L个用户编码,按照相似度从高到低排序
-
如果有相似度相同的可能好友,按照用户编号从小到大排序
-
如果推荐的好友个效不足L个,则推荐与用户K无无共同好友关系的用户(陌生人)作为可能好友,如果推荐仍不满足L个用户,剩余推荐用户编码使用0来占位
用例输入
6 7 3 2
1 2
1 3
2 3
3 4
3 5
4 5
5 6
用例输出
6 0
输入包含了6个用户,7条好友记录,给用户ID编号为3的用户推荐2个好友。
输出只有编号为6的用户可能是编号3用户的可能好友;
尝试推荐与编号3用户无共同好友的其他用户,由于除编号为6的用户之外,其他用户和编号3用户都是好友,所以找不到陌生人作为推荐的第二个用户;
推荐结果不足2个用户,所以推荐的第二个用户编码使用0来占位补足。
求解思路
我们首先可以利用哈希表构建用户之间的好友关系,方便在O(1)的时间复杂度内查找两个用户之间是否是好友关系
然后排序遍历就可以得到推荐列表了
#include<bits/stdc++.h>
using namespace std;
bool cmp(pair<int, int> a, pair<int, int> b) {if(a.second != b.second) return a.second > b.second;return a.first < b.first;
}
int main() {int N, M, K, L;scanf("%d %d %d %d", &N, &M, &K, &L);int x, y;int isf[1025][1025] = {0};for(int i = 0; i < M; i++) {scanf("%d%d", &x, &y);isf[x][y] = isf[y][x] = 1;}vector < pair<int, int> > sim;for(int i = 1; i <= N; i++) {if(i == K) continue;if(isf[K][i] != 1) {int cnt = 0;for(int j = 1; j <= N; j++) {if(i == j) continue;if(isf[K][j] == 1 && isf[i][j] == 1) cnt++;}sim.push_back(make_pair(i, cnt));}}sort(sim.begin(), sim.end(), cmp);int sum = 0;for(auto i : sim) {printf("%d ", i.first);sum++;}if(sum < L) {for(int i = sum; i < L; i++) printf("0 ");}return 0;
}
维修工
题目描述
维修工要给n个客户更换设备,为每个用户更换一个设备。维修工背包内最多装k个设备,如果背包里有设备可以直接前往下一个客户更换或回公司补充设备,没有则需要回公司取设备。这些客户有优先级,维修工需要按照优先级给客户更换设备,优先级level用数字表示,数字小的优先级高。维修工从公司出发,给n个客户更换设备,最后再返回公司。请计算维修工完成这项工作所需要经历的最短总距离是多少。维修工可以走斜线。
输入描述
第一行两个正整数 n,k(1≤k≤n≤2000),表示客户数和维修工背包容量。
第二行两个正整数 x,y ,用空格分隔(1 ≤ x , y ≤ 10^6),表示公司的坐标
接下来n行每行三个正整数 x i x_i xi, y i y_i yi, l e v e l i level_i leveli,用空格分隔(1≤ x i x_i xi, y i y_i yi≤10^6,1≤ l e v e l i level_i leveli<=n)。
( x i x_i xi, y i y_i yi)表示第i个客户的位置坐标, l e v e l i level_i leveli表示第 i i i个客户的优先级,保证所有客户优先级不同,客户和公司坐标不会重叠。
输出描述
输出最短总距离,结果四舍五入并保留一位小数,例如:9.0。
用例输入
3 2
1 1
3 1 1
1 2 2
3 2 3
用例输出
9.2
样例1解释:
从(1,1)->(3,1)->(1,1)->(1,2)->(3,2)->(1,1) = 2+2+1+2+√5 = 9.236
求解思路
题目的意思是维修工在维修完一家客户后,就会废掉背包内的一个设备(题面没讲清楚,一开始理解了好久背包内有设备为什么需要回公司取)。
因为本题规定了客户的优先级,因此我们首先将客户按照优先级进行排序。
接下来,我们可以按照记忆化搜索的方法,决定维修完当前客户后,到底回公司取设备再前往下一家客户还是直接去下一家客户维修。
我们采用memo数组记录每次的结果
memo[i + 1][k - 1] 表示回公司取完设备再前往下一家客户维修
memo[i + 1][j - 1] 表示背包内还有设备,直接前往下一家客户维修
#include<bits/stdc++.h>
using namespace std;double cal_dis(int x1, int y1, int x2, int y2) {return (double)sqrt(pow(x1 - x2, 2) + pow(y1 - y2, 2));
}const int maxn = 2001;
int n, k, cx, cy;struct customer
{int x, y, level;bool operator < (const customer& other) const { return level < other.level; }
}p[maxn];/*
记忆化搜索,假设memo[i][j]表示维修完第i个客户,并且背包中还剩下j个设备。
*/
vector <vector<double>> memo(maxn, vector<double>(maxn, 0)); double dfs(int i, int j) {if(memo[i][j] > 0) return memo[i][j];double dis = cal_dis(p[i].x, p[i].y, cx, cy);double ans = 99999999999.0;if(i < n - 1) {ans = min(ans, dfs(i + 1, k - 1) + dis + cal_dis(p[i + 1]. x, p[i + 1].y, cx, cy));// cout << dis + cal_dis(p[i + 1]. x, p[i + 1].y, cx, cy) << endl;if(j > 0) {ans = min(ans, dfs(i + 1, j - 1) + cal_dis(p[i + 1].x, p[i + 1].y, p[i].x, p[i].y));// cout << cal_dis(p[i + 1].x, p[i + 1].y, p[i].x, p[i].y) << endl;}} else { // 如果是最后一家,则修完直接回公司ans = dis;}return memo[i][j] = ans;
}int main() {scanf("%d%d", &n, &k);scanf("%d%d", &cx, &cy);for(int i = 0; i < n; i++) scanf("%d%d%d", &p[i].x, &p[i].y, &p[i].level);sort(p, p + n);dfs(0, k);double ans = dfs(0, k - 1) + cal_dis(p[0].x, p[0].y, cx, cy);printf("%.1f", ans);return 0;
}
维修工这个题是通过记忆化搜索求解最短路径的问题,想起之前在力扣上面刷到一个类似的题目,K站中转内最便宜的航班
题目链接
力扣上类似的题–K站中转内最便宜的航班
题目描述
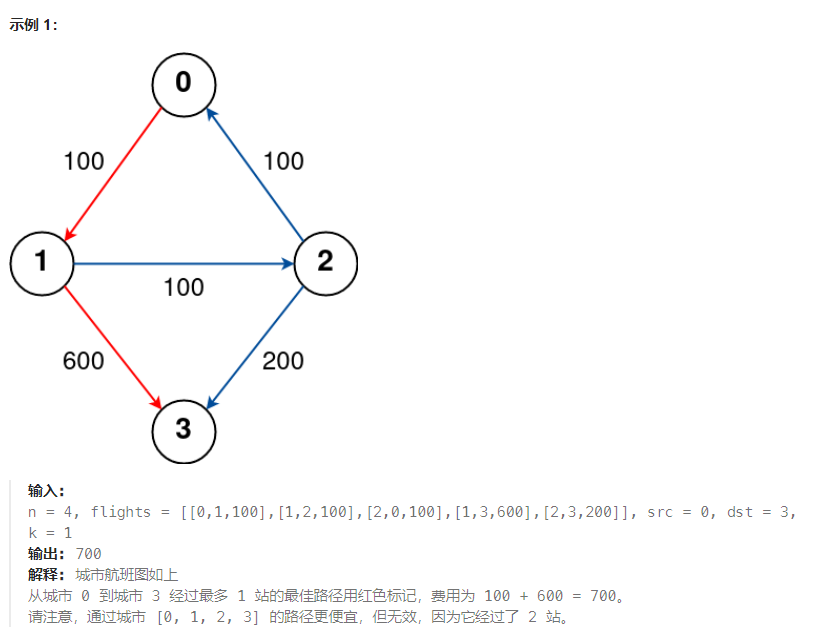
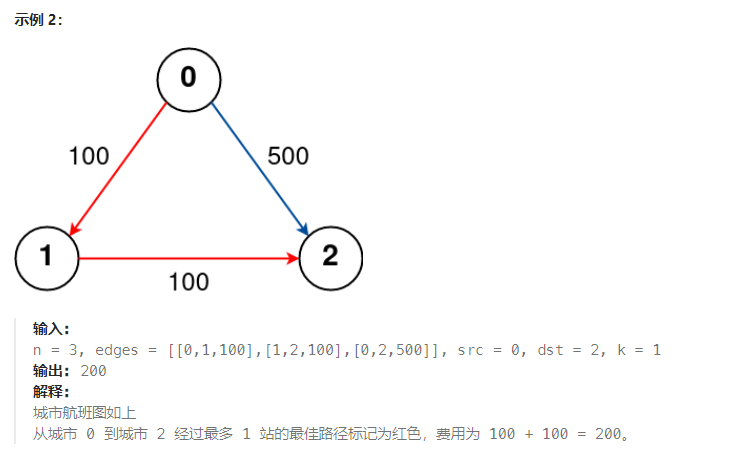
有 n 个城市通过一些航班连接。给你一个数组 flights ,其中 flights[i] = [fromi, toi, pricei] ,表示该航班都从城市 fromi 开始,以价格 pricei 抵达 toi。
现在给定所有的城市和航班,以及出发城市 src 和目的地 dst,你的任务是找到出一条最多经过 k 站中转的路线,使得从 src 到 dst 的 价格最便宜 ,并返回该价格。 如果不存在这样的路线,则输出 -1。
求解思路
和维修工一样,我们只需要利用记忆化搜索去寻找到第k个城市所需要的最少花费即可,注意k次中转的限制。
class Solution {
public:const int INF = 99999999;/*dp[i][j] 表示起点到城市i到达第j个城市的最少花费*/int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {vector <int> G[n]; // 构建邻接矩阵vector <vector<int>> price(n, vector<int>(n, INF));for(auto flight : flights) {G[flight[0]].push_back(flight[1]); price[flight[0]][flight[1]] = flight[2];}vector <vector<int>> dp(n, vector<int>(k + 2, 0));function<int(int, int)> dfs = [&](int i, int j) {if(dp[i][j] > 0) return dp[i][j];if(i == dst) {if(j <= k + 1) return dp[i][j];return INF;}int ans = INF;for(auto v : G[i]) {if(j < k + 1)ans = min(ans, dfs(v, j + 1) + price[i][v]);}return dp[i][j] = ans;};int ans = dfs(src, 0);return ans == INF ? -1 : ans;}
};
相关文章:

2024年华为9月4日秋招笔试真题题解
2024年华为0904秋招笔试真题 二叉树消消乐好友推荐系统维修工力扣上类似的题--K站中转内最便宜的航班 二叉树消消乐 题目描述 给定原始二叉树和参照二叉树(输入的二叉树均为满二叉树,二叉树节点的值范围为[1,1000],二叉树的深度不超过1000),…...

Next.js 14 App Router 预渲染 代码实践 静态页面渲染 SSG 服务端渲染代码 SSR
最近学习了Next.js 14框架,总结一下预渲染技术和具体代码用法,如果有理解不对的地方还请大佬指正。 注意以下内容只讨论App Router的新方案(getStaticProps已经弃用)。 1.简介 预渲染主要分为2种技术,静态页面渲染(…...

阿里云人工智能ACP错题整理.txt
1、TextRank是一种关键词抽取和文档摘要的排序算法,由谷歌的网页重要性排序算法PageRank算法改进而来,利用文本内部的词语间的语义便可以抽取关键词,它能够从一个给定的文本中抽取出该文本的关键词、关键词组,并使用抽取式的自动文…...

为 WebSocket 配置 Nginx 反向代理来支持 Uvicorn 的最佳实践
前景 要为WebSocket(以 ws:// 或 wss:// 协议)配置 Nginx 反向代理来代理 Uvicorn 服务器(或其他支持 WebSocket 的应用),需要确保 Nginx 和 Uvicorn 支持 WebSocket 连接,并做一些特定的配置。WebSocket 协议与 HTTP/HTTPS 不同,因此需要在 Nginx 中设置正确的代理头和…...

Centos7通过Docker安装openGauss5.0.2并配置用户供Navicat连接使用
下载镜像 [rootiZ2ze3qc9ouxm10ykn3cvdZ ~]# docker pull swr.cn-north-4.myhuaweicloud.com/ddn-k8s/docker.io/enmotech/opengauss:5.0.2 5.0.2: Pulling from ddn-k8s/docker.io/enmotech/opengauss 2ec76a50fe7c: Pull complete e48b50219b49: Pull complete 512e203af4…...

生成树详细配置(STP、RSTP、MSTP)
目录 一. 实验内容 STP配置实验 RSTP配置实验 MSTP配置实验 二. 1 ) STP配置实验 实验拓扑 编辑 实验配置 实验结果 2 ) RSTP配置实验 实验拓扑 实验配置 实验结果 3 ) MSTP配置实验 实验拓扑 实验配置 编辑 实验结果 三 实验总结 一. 实验内容 1) …...

服务器环境搭建-5 Nexus搭建与使用介绍
背景 本文介绍nexus的安装、配置和使用,之后通过案例的方式演示使用过程。 1.下载和安装 本文使用Nexus 3.x版本进行演示 下载地址:Download Nexus Repository OSS | Sonatype 国外网站下载速度较慢,也可以通过百度网盘下载(提取码:9999): …...
将 Parallels Desktop(PD虚拟机)安装在移动硬盘上,有影响吗?
当我们谈论在移动硬盘上安装 Parallels Desktop(简称PD虚拟机)及其对性能的影响时,特别是在运行如Unigraphics这样的资源密集型软件时,用户需要在便携性与性能之间找到最佳平衡。本文将深入探讨PD虚拟机装在移动硬盘有影响吗&…...

PHP智能化云端培训考试系统小程序源码
智能化云端培训考试系统:重塑学习评估的未来 🌟 引言:迈向智能教育的新时代 在这个日新月异的数字时代,教育也在经历着前所未有的变革。智能化云端培训考试系统的出现,正是这一变革的生动体现。它不仅打破了传统教育的…...

内幕!smardaten无代码平台全方位测评,这些细节你绝对想不到!
目录 一、引言二、测评要点2.1、前后端交互嵌套2.2、兼容性与可扩展性2.2.1、页面集成2.2.2、数据集成2.2.3、接口集成2.2.4、权限集成2.2.5、代码扩展支持 2.3、UI定制2.4、开发环境的隔离2.5、OEM定制2.6、多语言切换2.7、AI大模型能力 三、总结 一、引言 作为一枚IT从业者&…...

计算机专业的真正的就业情况
首先听到计算机行业,大多数人岗位已经饱和,前端已死,程序员35岁危机。但是事实上这些认知都是片面的,今天由我来为大家分析计算机行业的内幕。 疫情过后,过内各种行业都受到了冲击,你们敢说除了体制内的行业…...

Java对象列表属性映射工具类
背景 经常有这种情况,就是获取到一个对象列表之后,需要根据对象里某个字段的值去获取另一个字段的值。如下所示,有个Item对象列表,Item对象里有个id字段和Value字段,现需要根据id的值去查询value的值。 // 测试数据Li…...

.net core 通过Sqlsugar生成实体
通过替换字符串的方式生成代码,其他代码也可以通这种方式生成 直接上代码 设置模板 将这几个模板文件设置为:嵌入资源 模板内容: using SqlSugar;namespace {Namespace}.Domain.Admin.{ModelName}; /// <summary> /// {TableDisplay…...

ORCA-3D避障算法解析
二维ORCA原理参考: https://zhuanlan.zhihu.com/p/669426124 ORCA原理图解 1. 找到避障速度增量 u 碰撞处理分为三种情况: (1)没有发生碰撞,且相对速度落在小圆里 (2)没有发生碰撞࿰…...

CentOS 7停更官方yum源无法使用,更换阿里源
CentOS 7官方源已经停止维护,导致无法使用yum更新软件。通过尝试使用阿里云、清华大学等第三方源解决,现以阿里云第三方源进行配置: 1、备份原有的yum源配置文件 # cp -a /etc/yum.repos.d /etc/yum.repos.d.bak 2、删除原有的yum源配置文…...

Introduction结构
写好论文的**Introduction(引言)**部分是至关重要的,因为它为读者提供了背景信息,并引导他们进入论文的核心主题。一个优秀的引言应该具备以下几个关键要素: 1. 背景介绍 概述问题:首先,你需要…...

基于SpringBoot实现SpringMvc上传下载功能实现
SpringMvc上传下载功能实现 1.创建新的项目 1)项目信息填写 Spring Initializr (单击选中)Name(填写项目名字)Language(选择开发语言)Type(选择工具Maven)Group()JDK(jdk选择17 &…...

vue 控制组件是否显示
在Vue中,控制组件的显示通常使用v-if、v-else-if、v-else或v-show指令。 1.v-if:条件性地渲染元素,如果条件为假,元素甚至不会被渲染到DOM中。 <template><div><MyComponent v-if"showMyComponent" /&…...

生产部门不给力?精益化生产管理咨询公司为您出谋划策
问题背景 近年来,许多企业的生产部门面临着各种挑战和困难。生产效率低下、产品质量不稳定、生产成本过高等问题频频出现,给企业的发展带来了困扰。面对这一现状,许多企业开始寻求专业的管理咨询公司的帮助,以期能够通过精益生产…...

HTML+CSS - 网页布局之网格布局
1. dispaly设置 display是 CSS 中用于设置元素的显示方式的属性。它决定了元素如何被渲染到页面上。不同的display值会改变元素的显示行为,包括布局、排版以及对其他元素的影响。 其中网格容器是最常用的几种方式之一,在文档中创建类似于网格的效果&…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
