ORCA-3D避障算法解析

二维ORCA原理参考：
https://zhuanlan.zhihu.com/p/669426124

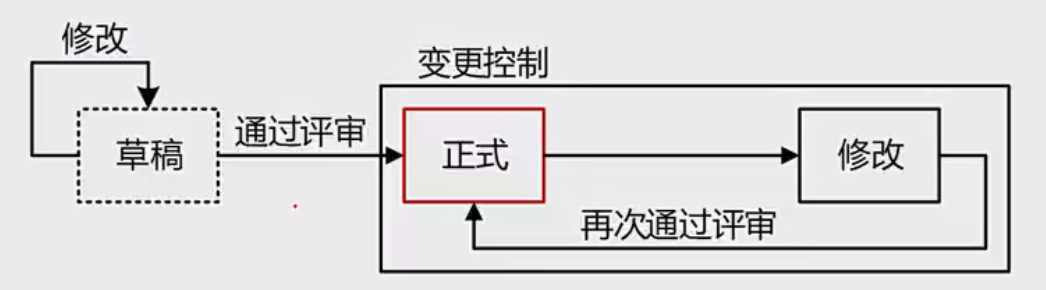
ORCA原理图解

1. 找到避障速度增量 u

碰撞处理分为三种情况：
（1）没有发生碰撞，且相对速度落在小圆里
（2）没有发生碰撞，且相对速度落在圆锥里
（3）发生碰撞，马上做出反应

timeStep 决定了仿真每一步的时间更新间隔，是系统的时间推进基础。较小的 timeStep 可以提高仿真的精度，但会增加计算量。

timeHorizon 决定了智能体在进行避障计算时预测的时间范围。较大的 timeHorizon 值使得智能体可以更早预测潜在碰撞，但会减少它的速度选择自由度。

timeStep 是碰撞时需要计算的调整u所需的时间
timeHorizon 是未发生碰撞时，需要计算的u所化的时间，他是一种提前预测

2. 添加速度障碍平面

表示一个平面需要法向量和平面上的点

1和2对应代码如下

	// 它使用ORCA（Optimal Reciprocal Collision Avoidance）方法来计算智能体之间的避碰行为void Agent::computeNewVelocity(){orcaPlanes_.clear();				  // 清空ORCA平面列表const float invTimeHorizon = 1.0f / timeHorizon_; // 计算时间视野的倒数/* 创建智能体的ORCA平面 */for (size_t i = 0; i < agentNeighbors_.size(); ++i){								       // 遍历每个邻居智能体const Agent *const other = agentNeighbors_[i].second;	       // 获取邻居智能体指针//这里的position_是在rvo->updateState添加的当前agent的位置// 改这块就好了===============================const Vector3 relativePosition = other->position_ - position_; // 计算相对位置const Vector3 relativeVelocity = velocity_ - other->velocity_; // 计算相对速度// const Vector3 relativePosition = relative_position_; // 计算相对位置// const Vector3 relativeVelocity = relative_velocity_; // 计算相对速度const float distSq = absSq(relativePosition);		       // 计算相对位置的平方距离const float combinedRadius = radius_ + other->radius_;	       // 计算合并半径const float combinedRadiusSq = sqr(combinedRadius);	       // 计算合并半径的平方Plane plane; // 定义一个平面对象Vector3 u;   // 定义速度调整向量if (distSq > combinedRadiusSq){										// 如果没有发生碰撞// w表示给定时间视野TimeHorizon内，两个智能题之间的相对速度偏移量const Vector3 w = relativeVelocity - invTimeHorizon * relativePosition; // 计算从截断中心到相对速度的向量const float wLengthSq = absSq(w);					// 计算w向量的平方长度const float dotProduct = w * relativePosition; // 计算w向量和相对位置的点积// 1. 如果投影在截断圆上// dotProduct表示相差的速度和相差的位置的点乘，要是点乘小于0，表示在靠近if (dotProduct < 0.0f && sqr(dotProduct) > combinedRadiusSq * wLengthSq){						    const float wLength = std::sqrt(wLengthSq); // 计算w向量的长度const Vector3 unitW = w / wLength;	    // 计算w向量的单位向量plane.normal = unitW;					 // 设置平面的法向量u = (combinedRadius * invTimeHorizon - wLength) * unitW; // 计算速度调整向量}// 2. 如果投影在圆锥上else{																  const float a = distSq;													  // 设置系数aconst float b = relativePosition * relativeVelocity;									  // 设置系数bconst float c = absSq(relativeVelocity) - absSq(cross(relativePosition, relativeVelocity)) / (distSq - combinedRadiusSq); // 设置系数c// t表示圆锥中心线到斜线的距离 对于 半径的倍数const float t = (b + std::sqrt(sqr(b) - a * c)) / a;									  // 计算t值const Vector3 w = relativeVelocity - t * relativePosition;								  // 计算w向量const float wLength = abs(w);												  // 计算w向量的长度const Vector3 unitW = w / wLength;											  // 计算w向量的单位向量plane.normal = unitW;			    // 设置平面的法向量u = (combinedRadius * t - wLength) * unitW; // 计算速度调整向量}}// 3. 如果发生碰撞else{									     const float invTimeStep = 1.0f / sim_->timeStep_;		     // 计算时间步长的倒数const Vector3 w = relativeVelocity - invTimeStep * relativePosition; // 计算w向量const float wLength = abs(w);					     // 计算w向量的长度const Vector3 unitW = w / wLength;				     // 计算w向量的单位向量plane.normal = unitW;				      // 设置平面的法向量u = (combinedRadius * invTimeStep - wLength) * unitW; // 计算速度调整向量}// 有多少个neighbor，就有多少个orca平面plane.point = velocity_ + 0.5f * u; // 计算平面上的点orcaPlanes_.push_back(plane);	    // 将平面添加到ORCA平面列表中}const size_t planeFail = linearProgram3(orcaPlanes_, maxSpeed_, prefVelocity_, false, newVelocity_); // 计算新的速度，如果失败返回失败的平面索引if (planeFail < orcaPlanes_.size()){									 // 如果存在失败的平面linearProgram4(orcaPlanes_, planeFail, maxSpeed_, newVelocity_); // 调用备用算法处理失败的平面}}

3. 线性规划求解出最优速度

linearProgram几个函数实现了一套线性规划（Linear Programming, LP）求解方法，目的是在有多个平面约束（即避障条件）的情况下找到最优的速度向量，以确保多个智能体不会发生碰撞。

linearProgram1()：寻找线与圆形区域的交点
linearProgram2()：解决单个平面约束的最优速度
linearProgram3()：求解所有平面的初步速度
linearProgram4()：处理多个平面之间的约束冲突