pointer-events
认识pointer-events属性
pointer-events是一个 CSS 属性,用于控制元素在鼠标事件中的表现。
一、可能的值
auto(默认值):
元素对鼠标事件的响应正常。鼠标可以与该元素进行交互,如点击、悬停等。none:
元素不对鼠标事件做出响应。鼠标事件会“穿透”该元素,好像该元素不存在一样。这对于在某些情况下需要让鼠标事件透过一个元素而作用于其后面的元素非常有用。
二、实际应用场景
- 禁用链接点击:
如果需要临时禁用一个链接,可以将其 pointer-events 设置为 none。这样,用户点击该链接时不会触发任何行为。
例如:
a.disabled-link { pointer-events: none; } - 覆盖鼠标事件:
当有多个元素重叠时,可以通过设置 pointer-events 来控制哪个元素响应鼠标事件。
比如,有一个半透明的覆盖层,希望用户在覆盖层显示时不能点击下面的元素,可以将覆盖层的 pointer-events 设置为 auto,下面元素的 pointer-events 设置为 none。 - 优化性能:
在某些情况下,将一些不相关的元素的 pointer-events 设置为 none 可以减少浏览器对鼠标事件的处理,从而提高性能。
相关文章:

pointer-events
认识pointer-events属性 pointer-events是一个 CSS 属性,用于控制元素在鼠标事件中的表现。 一、可能的值 auto(默认值): 元素对鼠标事件的响应正常。鼠标可以与该元素进行交互,如点击、悬停等。none: 元素…...

RAG 在企业应用中落地的难点与创新分享
在2024稀土开发者大会-AI Agent与应用创新分会上,我有幸分享了我们团队在企业应用中实施RAG(检索增强生成)的难点与创新。希望通过这篇文章,与大家探讨我们在实践中遇到的问题和解决方案,为从事相关工作的朋友提供一些…...

苹果CMS海洋CMS那个更容易被百度收录?苹果CMS站群
SEO优化和搜索引擎的友好性常常是网站管理员关注的重点。苹果CMS(maccmscn)和海洋CMS都是国内常见的CMS平台,但在搜索引擎优化(SEO)和百度收录方面,苹果CMS凭借其优秀的插件生态系统,特别是泛目…...

高教社杯数模竞赛特辑论文篇-2013年B题:碎纸复原模型与算法
目录 摘要 一、问题重述 二、问题分析 三、符号说明与模型假设 3.1 符号说明 3.2 模型假设 3.3 假设说明 四、模型的建立与求解 4.1 一维碎纸复原模型 4.1.1 图像的预处理 4.1.2 碎纸特征的提取 4.1.3 基于文字特征的识别序列 4.1.4 碎纸距离的定义 4.1.5 复原 TSP 问题 4.1.6 …...
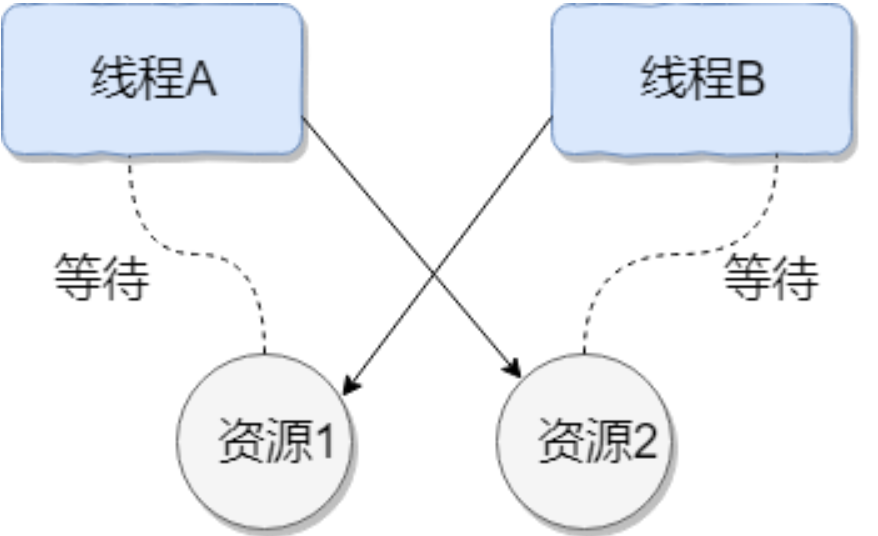
多线程面试题-28问
1、查询Java有哪些线程? public class MultiThread {public static void main(String[] args) {// 获取 Java 线程管理 MXBeanThreadMXBean threadMXBean ManagementFactory.getThreadMXBean();// 不需要获取同步的 monitor 和 synchronizer 信息,仅获…...

golang学习笔记16——golang部署与运维全攻略
推荐学习文档 golang应用级os框架,欢迎star基于golang开发的一款超有个性的旅游计划app经历golang实战大纲golang优秀开发常用开源库汇总golang学习笔记01——基本数据类型golang学习笔记02——gin框架及基本原理golang学习笔记03——gin框架的核心数据结构golang学…...

Unreal Fest 2024 虚幻引擎影视动画制作的普遍问题
———————————————————————————————————————— 本文为Unreal Fest Shanghai2024讲座内容笔记,非本人所著,原演讲人李文磊。 ————————————————————————————————————————…...

【机器学习-四-无监督学习unsupervise learning-聚类算法简介】
无监督学习unsupervise learning 聚类聚类的过程相似度度量方法聚类的方法划分式层次聚类基于密度的聚类 上一节讲的无监督学习,但是很多人可能会很疑惑,没有目标,那算法是怎么学会该怎样分类的呢?今天就简介一下其中的聚类算法。…...

IPv6路由基础
RIPng RIPng是一种较为简单的内部网关协议,是RIP在IPv6网络中的应用。RIPng主要用于规模较小的网络中,比如校园网以及结构较简单的地区性网络。由于RIPng的实现较为简单,在配置和维护管理方面也远比OSPFv3和IS-IS for IPv6容易,因…...

uniapp开发微信小程序 嵌套(uniapp开发/其他)H5,H5点击跳转微信小程序页面(通信
环境: uniapp开发微信小程序,嵌套webview,H5页面也是用的uniapp框架开发,H5页面点击商品后,需要跳转到微信小程序的详情页面 做法的原因 在微信小程序中使用web-view元素,如果要实现 H5到小程序的通信&am…...

VM虚拟机器配置网络DHCP服务
1、VM虚拟机器网络配置,centos 精简版没有配合网卡,如何配置网络 一、查看网卡信息 使用ip addr或ifconfig -a命令查看系统中现有的网卡设备名称,通常可能是eth0、ens33等类似的名称。 二、编辑网络配置文件 网络配置文件通常位于/etc/syscon…...

使用 jd.item_get API打造可读性商品介绍
在数字化时代,电子商务的蓬勃发展使得商品信息的获取变得至关重要。对于电商平台而言,如何准确、快速地获取商品信息,并以吸引人的方式呈现给消费者,成为提高销售额和用户体验的关键。本文将介绍如何利用 jd.item_get API 获取商品…...

java 通过文件下载地址读取文件内容
需求:读取文件内容,已知文件下载地址 需要引入pdfbox依赖 <dependency> <groupId>org.apache.pdfbox</groupId><artifactId>pdfbox</artifactId><version>2.0.27</version> </dependency>Override pub…...

打造古风炫酷个人网页:用HTML和CSS3传递笔墨韵味
需要用到的背景大家可以自己找喜欢的风格!!! 当然俺把俺用的背景放到文章最后了哦!!!!! 感谢关注和支持 长期更新哦~~~ 1. 简洁的页面布局:保持优雅和对称 在古风设计中,布局的对称性非常重要…...

vue 项目自适应 配置 px转rem 的插件postcss-pxtorem
1、安装 npm i postcss-plugin-px2rem --save -dev --force找到 postcss.config.cjs 没有的话就新建一个 module.exports {plugins: {// to edit target browsers: use "browserslist" field in package.jsonautoprefixer: {},"postcss-plugin-px2rem":…...

股票程序化交易是,第三方软件申请券商私有接口API的门槛
炒股自动化:申请官方API接口,散户也可以 python炒股自动化(0),申请券商API接口 python炒股自动化(1),量化交易接口区别 Python炒股自动化(2):获取…...

JDK8的一些主要的新特性
JDK8(Java Development Kit 8) 是一个重要的版本,带来了许多显著的特性和改进,极大地提升了 Java 语言的功能性和开发效率。以下是 JDK 8 的一些主要新特性: 一、Lambda 表达式 1.简化匿名内部类的写法,…...

40岁的java程序员,还有出路吗?
目录 前言一、现状与挑战二、出路与机遇三、案例分析与启示四、结语 前言 40岁Java程序员的出路:挑战与机遇并存 在科技日新月异的今天,IT行业始终保持着高速的发展态势,而Java作为其中的重要一员,其地位依然稳固且充满挑战。对…...

【服务器】shell脚本之Docker创建nginx
#!/bin/bash# 定义目标目录和配置文件路径 BASE_DIR"/opt/docker/nginx"ETC_DIR"$BASE_DIR/etc" ETC_CONF_DIR"$ETC_DIR/conf.d" SSL_DIR"$ETC_CONF_DIR/ssl" LOG_DIR"$BASE_DIR/log"HTML_DIR"$BASE_DIR/html"C…...

提取蛋白质复合体结构中组装体的变换矩阵
PDB文件中,组装体变换矩阵(assembly transformation matrices)用于描述多聚体结构中各个单体之间的相对位置和取向。从蛋白质复合体 PDB 数据中提取每个组装体(assembly)的变换矩阵,通常需要解析 PDB 文件中…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...
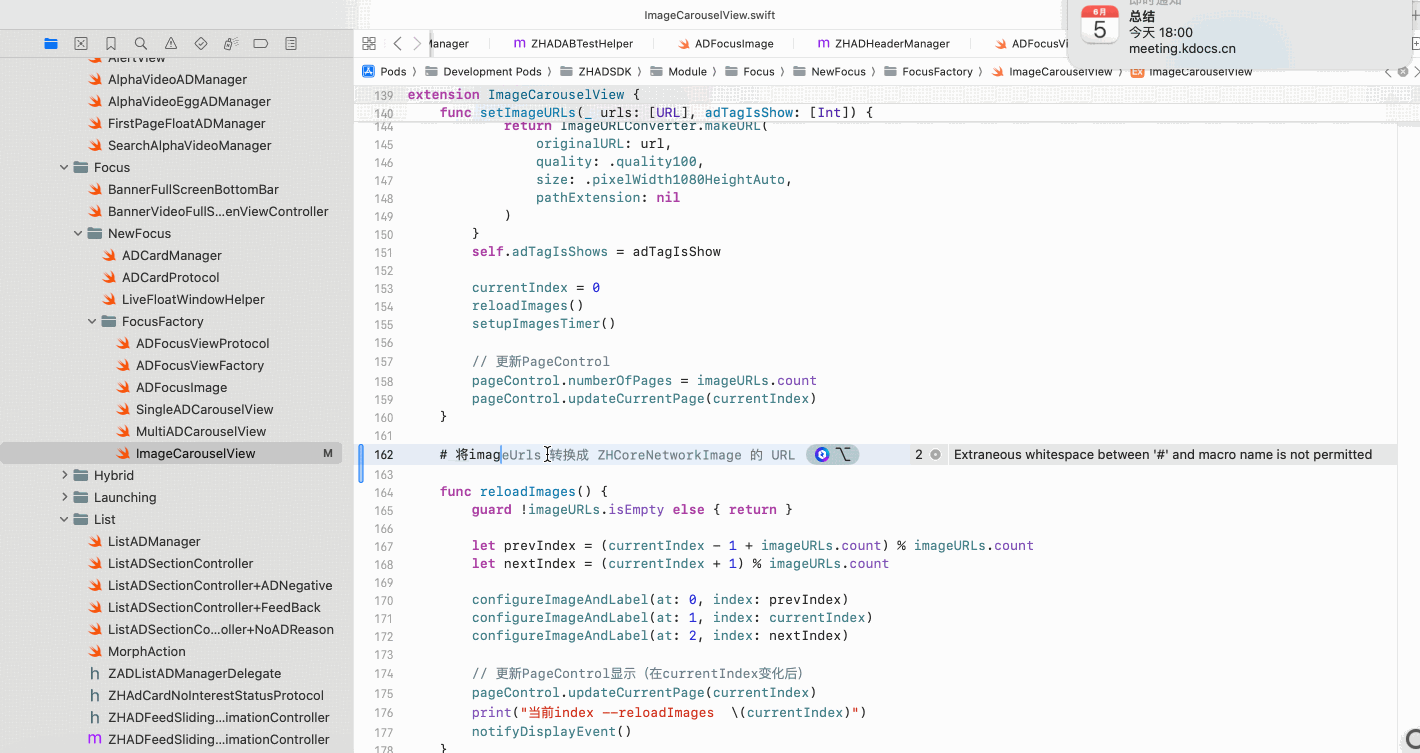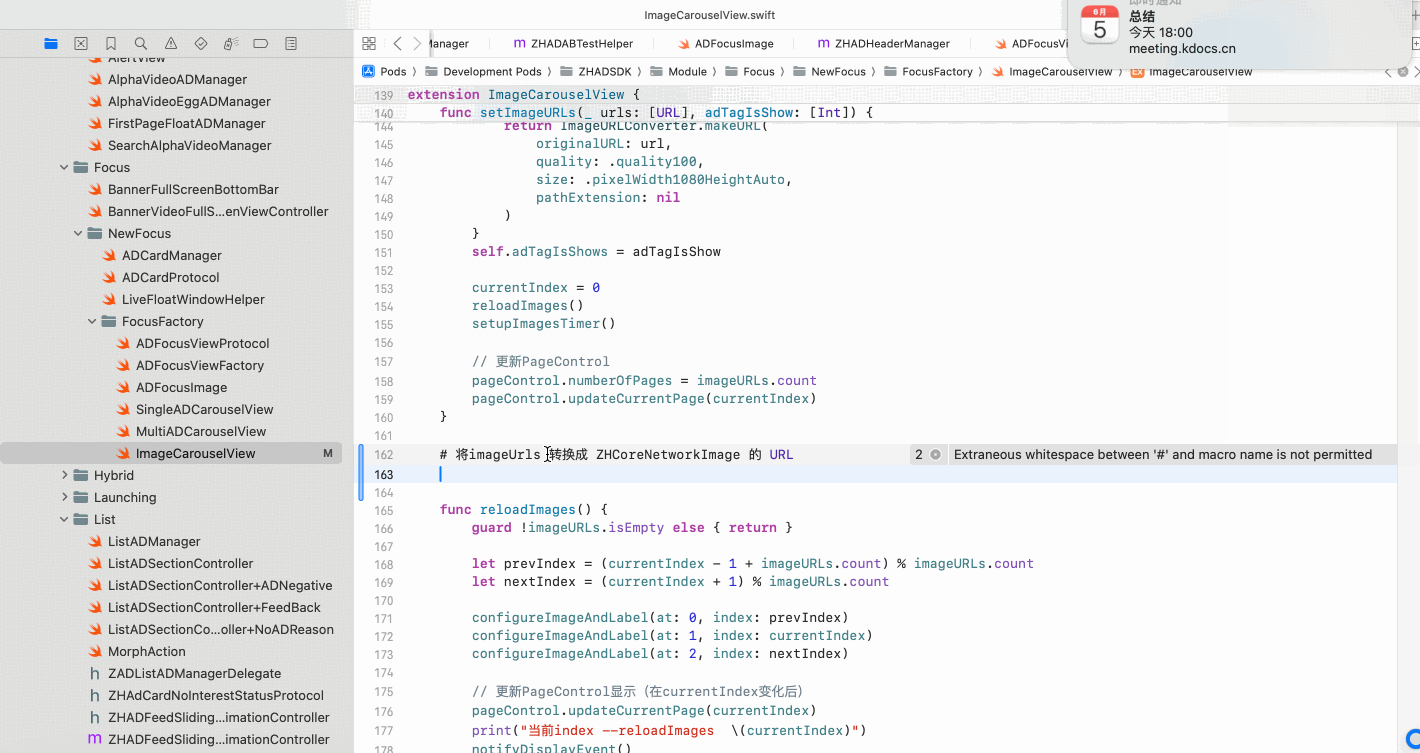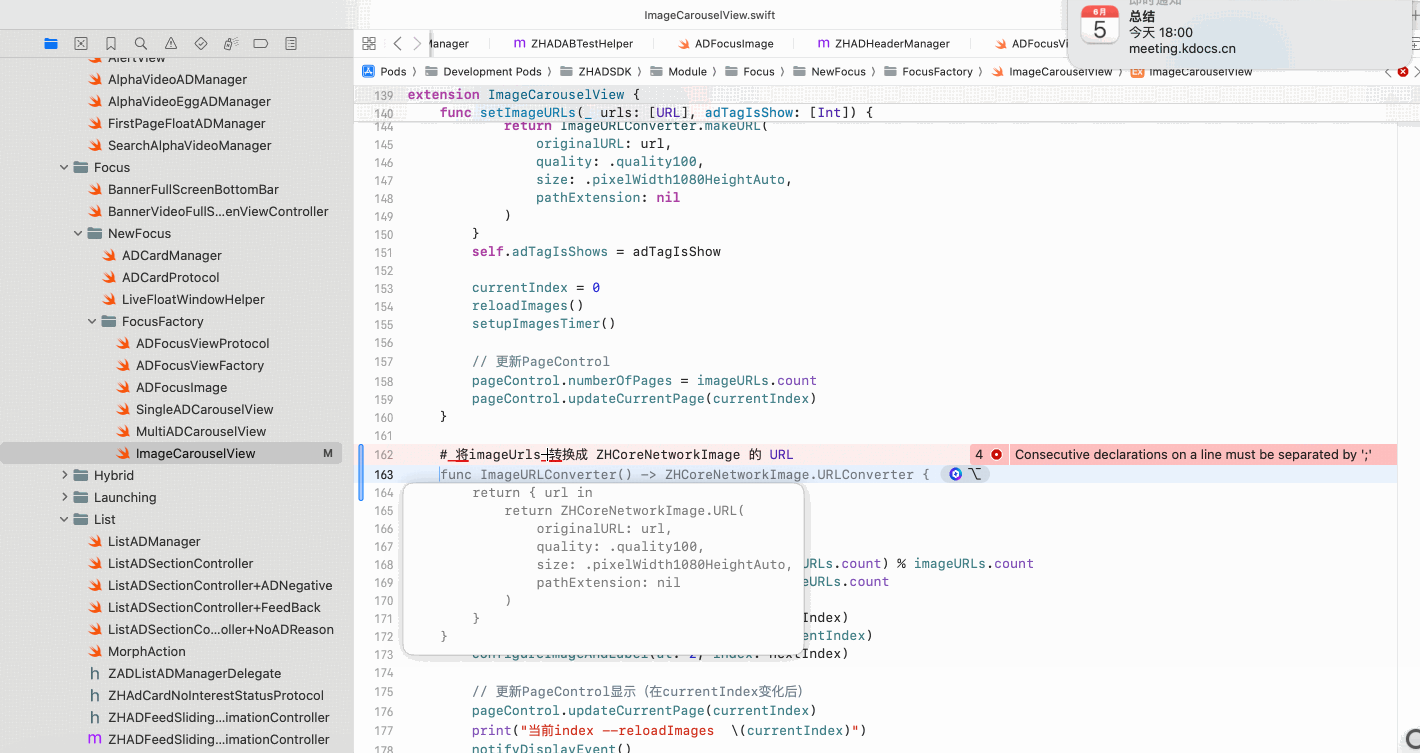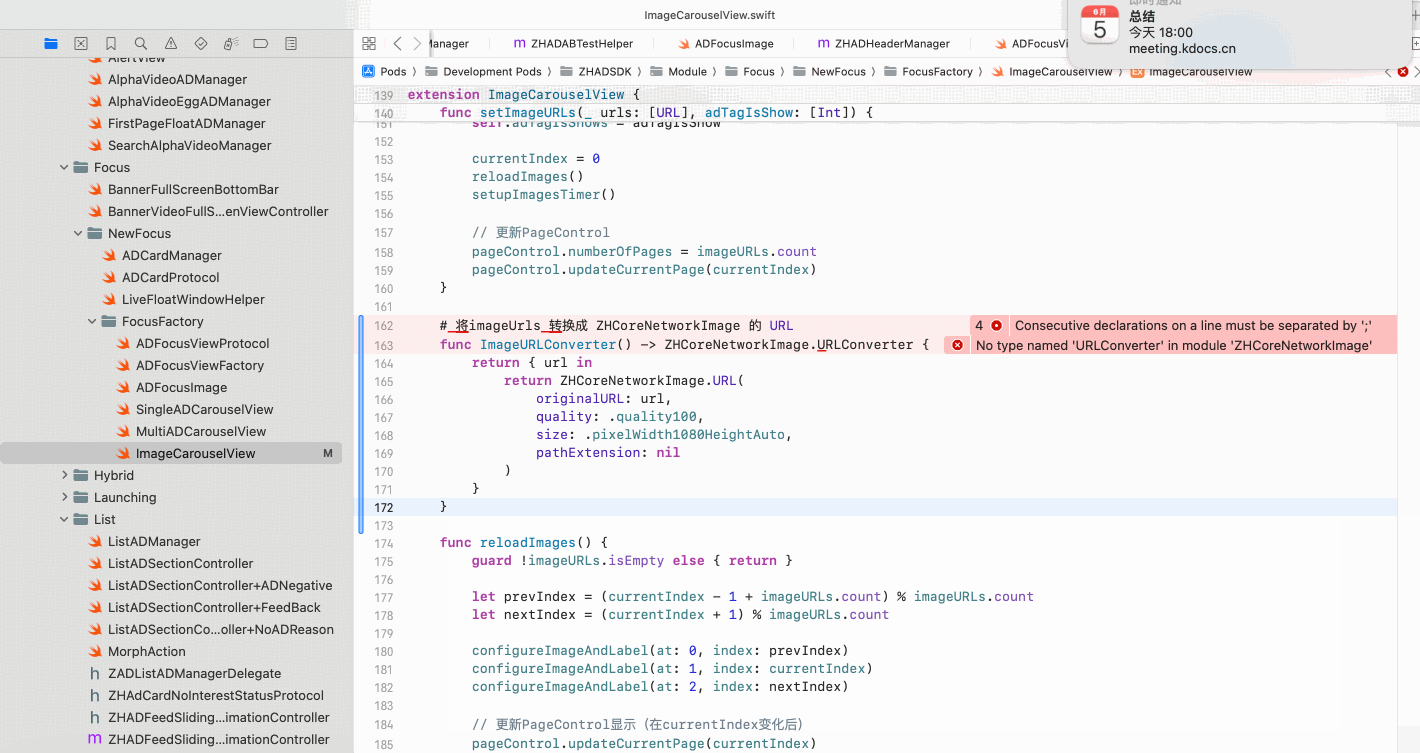
Copilot for Xcode (iOS的 AI辅助编程)
Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot,它能根据上下文补全代码,快速生成常用…...

npm安装electron下载太慢,导致报错
npm安装electron下载太慢,导致报错 背景 想学习electron框架做个桌面应用,卡在了安装依赖(无语了)。。。一开始以为node版本或者npm版本太低问题,调整版本后还是报错。偶尔执行install命令后,可以开始下载…...
