[实践应用] 深度学习之激活函数
文章总览:YuanDaiMa2048博客文章总览
深度学习之激活函数
- 激活函数
- 基本概念
- 分类
- 常见的激活函数
- 2. Tanh/双曲正切激活函数
- 3. ReLU激活函数
- 4. Softmax激活函数
- PyTorch中如何使用
- 1. 线性激活函数
- 2. 非线性激活函数
- Sigmoid
- Tanh
- ReLU
- Leaky ReLU
- Parametric ReLU (PReLU)
- 使用激活函数
激活函数
基本概念
激活函数(Activation Function)是一种添加到人工神经网络中的函数,旨在帮助网络学习数据中的复杂模式。在神经元中,输入的input经过一系列加权求和后作用于另一个函数,这个函数就是这里的激活函数。类似于人类大脑中基于神经元的模型,激活函数最终决定了是否传递信号以及要发射给下一个神经元的内容。
分类
激活函数可以分为线性激活函数(线性方程控制输入到输出的映射,如f(x)=x等)以及非线性激活函数(非线性方程控制输入到输出的映射,比如Sigmoid、Tanh、ReLU、LReLU、PReLU、Swish 等)
为什么要使用激活函数?
- 因为神经网络中每一层的输入输出都是一个线性求和的过程,下一层的输出只是承接了上一层输入函数的线性变换,所以如果没有激活函数,那么无论你构造的神经网络多么复杂,有多少层,最后的输出都是输入的线性组合,纯粹的线性组合并不能够解决更为复杂的问题。而引入激活函数之后,我们会发现常见的激活函数都是非线性的,因此也会给神经元引入非线性元素,使得神经网络可以逼近其他的任何非线性函数,这样可以使得神经网络应用到更多非线性模型中。

常见的激活函数
- Sigmoid函数
Sigmoid函数也被称为Logistic函数,通常用于神经网络的隐层神经元输出。其输出值的范围在 (0,1) 之间,因此可以将实数映射到 (0,1) 的区间,常用于二分类问题。在特征相差较复杂或差异不是特别大时,Sigmoid函数的效果较好。其数学表达式如下所示:
σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1 + e^{-x}} σ(x)=1+e−x1

应用场景
- 用于将预测概率作为输出的模型。由于概率的取值范围是 0 到 1,因此 Sigmoid 函数非常合适。
- 适用于二分类问题,输出范围为 (0,1),可用于输出概率。
- 适用于多层网络中的中间层的非线性转换。优点
- 输出范围在 (0,1) 内,适合作为概率输出。
- 函数是可微的,有助于梯度下降优化。
- 在输出接近 0 或 1 时,梯度较大,有助于参数更新。
缺点
- Sigmoid 函数存在梯度消失问题,导致深层网络训练困难。
- 在输出远离中心位置时,梯度接近于 0,容易导致梯度消失。
- Sigmoid 函数的计算相对复杂,会消耗更多的计算资源。
2. Tanh/双曲正切激活函数
Tanh函数,又称双曲正切激活函数(hyperbolic tangent activation function),与Sigmoid函数类似,但将其值范围压缩至 -1 到 1 的区间内。与Sigmoid函数不同的是,Tanh函数的输出以零为中心,因为其取值范围在 -1 到 1 之间。其数学表达式如下:
Tanh ( x ) = e x − e − x e x + e − x \text{Tanh}(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} Tanh(x)=ex+e−xex−e−x
Tanh函数和Sigmoid函数之间存在一种简单的关系,可以通过Sigmoid函数的输出来表示Tanh函数。给定Sigmoid函数的输出 σ ( x ) σ(x) σ(x),Tanh函数的输出可以表示为:
Tanh ( x ) = 2 σ ( 2 x ) − 1 \text{Tanh}(x) = 2σ(2x) - 1 Tanh(x)=2σ(2x)−1
这个关系式表示了Tanh函数如何由Sigmoid函数的输出得出。

应用场景
- 适用于隐藏层的激活函数,可以将输入值映射到 (-1,1) 区间内。
- 适用于需要零中心化的场景,相较于 Sigmoid 函数,Tanh 函数的输出以 0 为中心。
优点
- 输出值在 (-1,1) 内,相比于 Sigmoid 函数,Tanh 函数的输出以 0 为中心,有助于神经网络的训练。
- 函数的形状对称,能够保持输入的符号信息。
缺点
- 仍然存在梯度消失问题,特别是在靠近饱和区域时。
- 计算复杂度较高,相比于 Sigmoid 函数,计算量大一些。
3. ReLU激活函数
ReLU函数又称为修正线性单元(Rectified Linear Unit),是一种分段线性函数,其弥补了sigmoid函数以及tanh函数的梯度消失问题,在目前的深度神经网络中被广泛使用。ReLU函数本质上是一个斜坡(ramp)函数,其数学表达式如下:
- 这个函数的图像在 x > 0 x > 0 x>0 时是一条斜坡,斜率为1;在 x < 0 x < 0 x<0 时函数值为0。ReLU 函数可以表示为:
ReLU ( x ) = { 0 , if x ≤ 0 x , if x > 0 = max ( 0 , x ) \text{ReLU}(x) = \begin{cases} 0, & \text{if } x \leq 0 \\ x, & \text{if } x > 0 \end{cases} = \max(0, x) ReLU(x)={0,x,if x≤0if x>0=max(0,x)
ReLU函数作为神经元的激活函数,在接收来自上一层神经网络的输入向量 x \mathbf{x} x,进行线性变换 w T x + b \mathbf{w}^T\mathbf{x} + b wTx+b 之后,产生非线性输出结果。换言之,对于进入神经元的来自上一层神经网络的输入向量 x \mathbf{x} x,使用ReLU函数的神经元会输出:
ReLU ( w T x + b ) = max ( 0 , w T x + b ) \text{ReLU}(\mathbf{w}^T\mathbf{x} + b) = \max(0, \mathbf{w}^T\mathbf{x} + b) ReLU(wTx+b)=max(0,wTx+b)
这个输出值将被传递至下一层神经元,或作为整个神经网络的输出(取决于神经元在网络结构中的位置)。

应用场景
- 在深度神经网络中广泛应用,能够有效避免梯度消失问题,加速网络的收敛速度。
- 许多成功的深度学习模型使用 ReLU 作为激活函数,如 AlexNet、VGG 等。
优点
- 相比于 Sigmoid 和 Tanh 函数,ReLU 函数的计算速度更快,因为它是简单的线性函数。
- 解决了梯度消失问题,能够在训练深层神经网络时更快地收敛。
缺点
- Dead ReLU 问题:当输入为负时,ReLU 函数输出为 0,导致部分神经元失活,无法更新参数,影响模型性能。
- 对于负数部分,ReLU 函数的导数为 0,可能导致梯度消失问题。
- 不是零中心化,可能导致在训练过程中出现偏移。
Dead ReLU问题是指在训练神经网络时,ReLU激活函数所对应的神经元可能会因参数更新不当而“死亡”。具体来说,如果某个ReLU神经元在一次不恰当的参数更新后,对于所有的训练数据,其输出始终为负数,那么该神经元的参数梯度将永远为零,即无法被激活。这意味着,即使在后续的训练过程中,神经元接收到的输入值可能已经可以激活它,但由于参数梯度一直为零,该神经元也无法被激活。这种情况被称为“死亡ReLU问题”,可能出现在网络的任何隐藏层中。Dead ReLU问题可能会影响网络的性能和训练效果,因此在实践中需要采取措施来缓解这个问题,例如使用其他类型的激活函数或调整网络结构。
4. Softmax激活函数
Softmax函数是一种常用的激活函数,通常用于多分类问题中,将模型的原始输出转换为概率分布。Softmax函数接受一个包含任意实数的向量作为输入,并将每个元素的值转换为介于 0 和 1 之间的概率值,使得所有元素的概率之和等于 1。Softmax函数的数学表达式如下:
Softmax ( z ) i = e z i ∑ j = 1 N e z j \text{Softmax}(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{j=1}^{N} e^{z_j}} Softmax(z)i=∑j=1Nezjezi
其中, z \mathbf{z} z 是输入向量, N N N 是向量的维度, Softmax ( z ) i \text{Softmax}(\mathbf{z})_i Softmax(z)i 表示 Softmax 函数的输出向量中的第 i i i 个元素。
应用场景
- 用于多分类问题中,将模型的原始输出转换为类别概率分布。
- 在神经网络的输出层使用 Softmax 函数,可以得到每个类别的预测概率,然后根据概率进行分类决策。
优点
- 输出结果是一个概率分布,所有类别的概率之和为 1,便于理解和解释。
- Softmax 函数是可微的,有助于梯度下降优化。
- 在训练过程中,Softmax 函数的梯度可以直接用于更新参数。
缺点
- 对于输入较大或较小的情况,Softmax 函数的输出会非常接近于 0 或 1,可能导致梯度消失问题。
- Softmax 函数的计算量较大,因为要对所有元素进行指数运算和求和操作,特别是在处理大规模数据时,计算复杂度较高。
PyTorch中如何使用
在 PyTorch 中,可以使用 torch.nn 模块来定义各种激活函数。以下是几个经典激活函数的定义及其代码示例:
1. 线性激活函数
线性激活函数实际上是恒等函数,它可以通过直接返回输入实现:
import torch.nn as nnclass LinearActivation(nn.Module):def forward(self, x):return xlinear_activation = LinearActivation()
2. 非线性激活函数
Sigmoid
import torch.nn as nnsigmoid = nn.Sigmoid()
Tanh
import torch.nn as nntanh = nn.Tanh()
ReLU
import torch.nn as nnrelu = nn.ReLU()
Leaky ReLU
import torch.nn as nnleaky_relu = nn.LeakyReLU(negative_slope=0.01) # negative_slope 参数用于控制负半轴的斜率
Parametric ReLU (PReLU)
import torch.nn as nnprelu = nn.PReLU() # PReLU 的参数可以通过设置 init 参数进行初始化
使用激活函数
可以在构建模型时将这些激活函数作为层添加到网络中。例如:
import torch
import torch.nn as nnclass SimpleNet(nn.Module):def __init__(self):super(SimpleNet, self).__init__()self.fc1 = nn.Linear(10, 20)self.relu = nn.ReLU() # 可以换成其他激活函数,如 nn.Sigmoid()self.fc2 = nn.Linear(20, 1)def forward(self, x):x = self.fc1(x)x = self.relu(x)x = self.fc2(x)return x# 实例化模型
model = SimpleNet()
相关文章:

[实践应用] 深度学习之激活函数
文章总览:YuanDaiMa2048博客文章总览 深度学习之激活函数 激活函数基本概念分类常见的激活函数2. Tanh/双曲正切激活函数3. ReLU激活函数4. Softmax激活函数 PyTorch中如何使用1. 线性激活函数2. 非线性激活函数SigmoidTanhReLULeaky ReLUParametric ReLU (PReLU) 使…...

Java基础之数组
文章地址:Java基础之数组 码农爱刷题 为计算机编程爱好者和从业人士提供技术总结和分享 !为前行者蓄力,为后来者探路!...
基于SpringBoot+Vue的智慧自习室预约管理系统
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、SSM项目源码 系统展示 【2025最新】基于JavaSpringBootVueMySQL的…...

pptpd配置文件/etc/pptpd.conf详解
正文共:1111 字 2 图,预估阅读时间:1 分钟 如果要在Linux系统配置PPTP(Point-to-Point Tunneling Protocol,点到点隧道协议)VPN,一般是使用pptpd软件。pptpd命令通常从配置文件/etc/pptpd.conf中…...
springboot对数据库进行备份+对一个文件夹内的文件按时间排序,只保留最近的8个文件
首先,对数据库进行备份,用到的命令: mysqldump --opt -h 192.168.1.200 --userroot --passwordxxx --result-fileE://data//20240911141400.sql --default-character-setutf8 xxx(数据库名) 直接上代码 配置文件部分…...

【软考中级攻略站】-软件设计师(4)-计算机网络基础
计算机网络的分类 1. 局域网(Local Area Network, LAN) 局域网是指在一个较小的地理区域内连接的计算机网络,比如学校的机房、公司的办公室或者家里的Wi-Fi网络。在这个网络内的计算机可以直接相互通信,速度很快,延迟…...
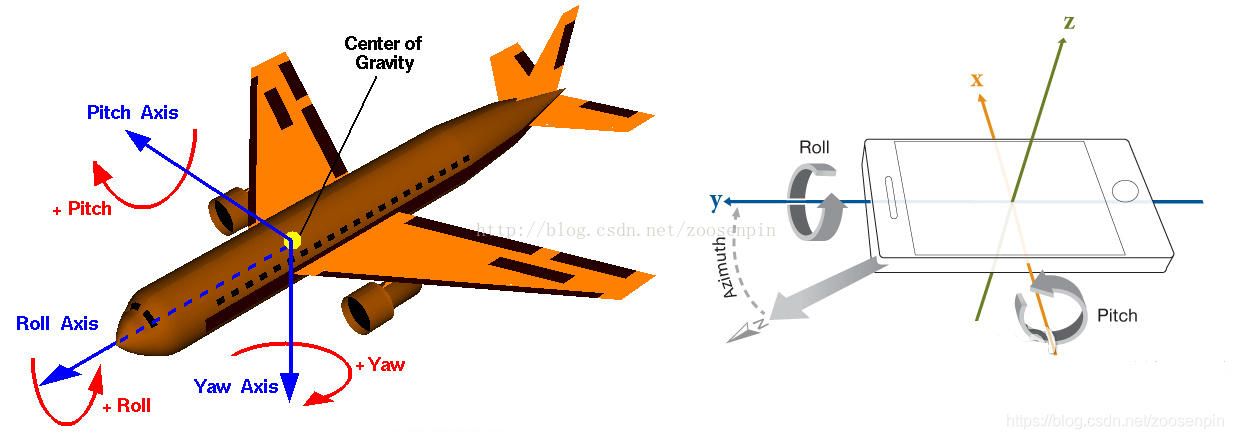
Android以及IoT设备传感器软件开发总结
1 传感器选型 1.1 传感器选型 6 axis:Bosch BMI160(比较差),InvenSense MPU6050(DMP),ST LSM6Dxx Acc: Freescale MMA7450L (MicroMachined Accelerometer/MC Multi-Axis, iMX31), Kionix KXSD9…...

Vue2/Vue3中编程式路由导航实践总结
【1】Vue2编程式路由导航 ① router.push 除了使用 <router-link> 创建 a 标签来定义导航链接,我们还可以借助 router 的实例方法,通过编写代码来实现。 router.push(location, onComplete?, onAbort?)注意:在 Vue 实例内部&#…...

【nginx】ngx_http_proxy_connect_module 正向代理
50.65无法访问 服务器, (403 错误) 50.196 可以访问服务器。 那么,配置65 通过196 访问。 需要一个nginx作为代理 【nginx】搭配okhttp 配置反向代理 发送原生的nginx是不支持okhttp的CONNECT请求的。 大神竟然给出了一个java工程 GINX编译ngx_http_proxy_connect_module及做…...

单考一个OCP认证?还是OCP和OCM认证都要考?
Oracle的OCP认证是数据库行业非常经典的一个认证,从事数据库行业的人都建考一个 Oracle OCP 认证。 OCP认证内容包括: OCA部分:数据库基础知识、SQL 语言使用、基本的数据库管理技能等,如数据库安装与配置、理解数据库架构、…...

在Spring官网查看Springboot与Java的版本对应关系
查看Spring Boot与Java的版本对应关系,可以按照以下步骤操作: 访问Spring官方网站,进入Spring Boot项目页面。可以通过点击菜单中的“Projects”,然后选择“Spring Boot”来访问。Spring | Home 在Spring Boot的LEARN页签中&…...
——数据管理(一)分布式数据)
HarmonyOS学习(十二)——数据管理(一)分布式数据
文章目录 1、分布式数据服务概述2、KV数据模型(键值对数据库)3、分布式数据服务的约束和限制4、接口说明5、分布式数据服务开发步骤5.1、导入模块5.2、构造分布式数据库管理类实例5.3、获取、创建分布式数据库5.4、订阅分布式数据库的数据变化5.5、插入数…...

3D GS 测试自己的数据
环境配置 win11 vs2019cuda11.8driver522.06python3.10pytorch 2.4.0colmap3.8(可选,用于将图像生成点云) 安装 1 minicodagit 略 2 vs2019 在装cuda前安装, 选择c桌面开发即可, 环境变量path中配置C:\Program…...

攻防世界 supersqli
supersqli 一般sql语句的题都是先判断,经过测试,是单引号注入 999 union select database(),2#可以发现很多关键字都被过滤了select,所以联合查询,报错注入,布尔和时间盲注都不能用了,可以想到堆叠注入。…...

OceanBase 运维管理工具 OCP 4.x 升级:聚焦高可用、易用性及可观测性
可视化的管控平台,对 OceanBase 这类的分布式数据库及大规模数据的运维管理来说,是提升运维效率与数据库管理水平的重要工具。OceanBase 运维管理工具 OCP 作为专为OceanBase数据库设计的企业级全生命周期管理平台,为用户提供了全面的数据库可…...

HarmonyOS应用开发( Beta5.0)HOS-用户认证服务:面部识别
介绍 User Authentication Kit(用户认证服务)提供了基于用户在设备本地注册的人脸和指纹来认证用户身份的能力。 用户向应用/系统服务请求访问某些个人数据或执行某些敏感操作时,应用/系统服务将调用系统用户身份认证控件对用户身份进行认证…...

解决Docker镜像不可下载
使用国内可信的镜像中心 可信国内镜像网址:https://hub.atomgit.com/ 点击镜像仓库 搜索想要的镜像 按如图所示,即可查看对应的版本 点击复制,即可下载使用 缺点: 可用的镜像相比于docker官方量少 并且,获取的镜像名字…...

考研报名确认上传身份证户口本学历证明照片如何压缩裁剪
随着考研季节的到来,数以万计的考生开始准备报名所需的各种材料。在这一过程中,证件照片的上传无疑是一个关键环节。正确的照片格式和尺寸不仅能确保报名流程的顺利进行,还能避免因材料不合格而造成的不必要麻烦。本文将详细介绍如何在考研报…...

DolphinScheduler应用实战笔记
DolphinScheduler应用实战笔记 一、前言二、DS执行SQL或存储过程二、DS调用DataX同步数据三、DS调用HTTP接口四、DS依赖(DEPENDENT)节点五、DS SPARK 节点六、DS Flink 节点七、DS Flink 节点八、DS SQL 节点九、DS Java程序十、DS Python节点 一、前言 DolphinScheduler&…...

IThenticate查重为何成为英语期刊论文投稿首选工具
发表一篇英语论文,我发现很多人在准备向期刊投稿之前,都会选择使用IThenticate查重系统对论文进行相似性检测。是什么魔力,让这个查重工具让投稿者如此偏爱使用它查重呢? 一、什么是IThenticate查重系统? 在了解它被…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里
写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...
