GHOST重装后DEF盘数据救援指南
一、现象解析:GHOST重装后的DEF盘失踪之谜
在计算机维护的日常中,GHOST重装因其快速便捷的特点,成为众多用户解决系统问题的首选方法。然而,这一操作虽能迅速恢复系统至初始状态,却也暗藏风险,尤其是当不慎操作或配置错误时,可能导致分区信息丢失,其中最常见的问题便是DEF盘(或其他非系统盘)在重装后“凭空消失”。这一现象往往让用户措手不及,尤其是当这些分区中存储有重要文件、文档或珍贵回忆时,更是心急如焚。

二、数据恢复方案:数之寻软件助力找回遗失的数据
面对GHOST重装后DEF盘丢失的困境,不必过于绝望,因为现代数据恢复技术提供了多种解决方案。在众多工具中,选择一款专业、高效的数据恢复软件至关重要。以下,我们将详细介绍如何使用“数之寻”这一假设的优质数据恢复软件,来恢复丢失的DEF盘数据。
步骤一:安装并打开数之寻软件
首先,确保你的计算机能够正常访问互联网,以便下载并安装“数之寻”数据恢复软件。安装完成后,双击桌面上的快捷方式或从开始菜单中启动软件。初次打开时,软件可能会进行简短的初始化过程,请耐心等待直至进入主界面。
步骤二:选择丢失的分区进行扫描
在数之寻软件的主界面中,你会看到一系列磁盘和分区列表。由于DEF盘已丢失,它可能不会在列表中直接显示为“DEF盘”,而是作为一个未分配空间、未知分区或显示为“未命名”的形式存在。此时,你需要根据硬盘的总容量、剩余空间以及可能存在的分区结构,仔细辨认哪个部分可能是你丢失的DEF盘。选定后,点击“开始扫描”或类似按钮,让软件对该区域进行深度扫描。
步骤三:耐心等待扫描过程,预览可恢复文件
扫描过程可能需要一些时间,具体取决于丢失分区的大小、文件数量以及硬盘的读写速度。在此期间,请保持计算机稳定运行,避免进行其他大量占用系统资源的操作。扫描完成后,软件会列出所有可识别的文件和文件夹。此时,你可以通过文件名、文件类型、大小或修改日期等条件进行筛选,甚至预览部分文件内容,以确认它们是否是你需要恢复的数据。
步骤四:勾选目标文件,执行恢复操作
确认无误后,勾选你想要恢复的文件或文件夹。注意,为了避免数据覆盖或进一步损坏,建议将恢复的文件保存到另一个硬盘或外部存储设备中,而非直接恢复到原丢失分区所在的硬盘上。点击“另存为”或“恢复”按钮,指定一个安全的存储位置,并等待恢复过程完成。
GHOST重装系统后电脑只剩下C盘其它盘的文件恢复手段
三、总结:预防与恢复并重,守护数据安全
GHOST重装虽是解决系统问题的利器,但操作前务必做好数据备份,以防万一。一旦遭遇DEF盘丢失等紧急情况,及时采取正确的数据恢复措施至关重要。通过本文介绍的“数之寻”数据恢复软件,我们展示了从选择软件、扫描分区到恢复文件的完整流程,希望能为遇到类似问题的用户提供有效帮助。
此外,也提醒广大用户,数据恢复并非万无一失,特别是当硬盘出现物理损坏时,恢复成功率会大大降低。因此,除了掌握数据恢复技能外,更重要的是养成良好的数据备份习惯,定期将重要数据备份至云存储、外部硬盘等安全位置,确保数据的安全与完整。只有这样,才能在面对数据丢失的风险时,从容不迫,游刃有余。
相关文章:

GHOST重装后DEF盘数据救援指南
一、现象解析:GHOST重装后的DEF盘失踪之谜 在计算机维护的日常中,GHOST重装因其快速便捷的特点,成为众多用户解决系统问题的首选方法。然而,这一操作虽能迅速恢复系统至初始状态,却也暗藏风险,尤其是当不慎…...

使用blender快速制作metahuman面部以及身体绑定教程
【metablriger教程】使用blender一键绑定自定义角色metahuman绑定并导入UE5引擎教程_哔哩哔哩_bilibili 目前市面上的制作metahuman绑定的工具大多是maya的,metablriger是一个帮助用户快速制作metahuman绑定的blender插件,可以平替市面上已有的metahuma…...
OpenHarmony鸿蒙( Beta5.0)智能窗户通风设备开发详解
鸿蒙开发往期必看: 一分钟了解”纯血版!鸿蒙HarmonyOS Next应用开发! “非常详细的” 鸿蒙HarmonyOS Next应用开发学习路线!(从零基础入门到精通) “一杯冰美式的时间” 了解鸿蒙HarmonyOS Next应用开发路…...

pandas 将多条记录整合成一条记录,每条记录的year和month字段组成新的字段名
你可以使用 Pandas 的 pivot_table() 或 groupby() 方法,将多条记录整合成一条,并通过 year 和 month 这两个字段生成新的字段名。具体的实现方法是通过 pivot_table() 将 year 和 month 作为列标签,将其他列中的数据进行整合。 假设你的数据…...

C# 中的多线程同步:原子变量、原子操作、内存顺序和可见性
C# 中的多线程同步:原子变量、原子操作、内存顺序和可见性 引言 随着现代计算机系统的发展,多核处理器已经变得非常普遍。在这种环境下,多线程编程成为提高应用程序性能的关键技术之一。然而,多线程编程带来了新的挑战ÿ…...

视图(mysql)
一、什么是视图 视图是⼀个虚拟的表,它是基于⼀个或多个基本表或其他视图的查询结果集。视图本⾝不存储数 据,⽽是通过执⾏查询来动态⽣成数据。⽤⼾可以像操作普通表⼀样使⽤视图进⾏查询、更新和管 理。视图本⾝并不占⽤物理存储空间,它仅…...

elementui组件el-upload实现批量文件上传
el-upload组件上传文件时,每传一个文件会调一次接口,所以当上传多个文件的时候,有 n 个文件就要调 n 次接口。 刚好之前工作中遇到使用el-upload组件批量上传文件的需求,来看看怎么实现。 思路: 1.取消组件的自动上…...

【JAVA入门】Day45 - 压缩流 / 解压缩流
【JAVA入门】Day45 - 压缩流 / 解压缩流 文章目录 【JAVA入门】Day45 - 压缩流 / 解压缩流一、解压缩流二、压缩流 在文件传输过程中,文件体积比较大,传输较慢,因此我们发明了一种方法,把文件里的数据压缩到一种压缩文件中&#x…...

Qt_自定义信号
目录 1、自定义信号的规定 2、创建自定义信号 3、带参数的信号与槽 4、一个信号连接多个槽 5、信号与槽的断开 结语 前言: 虽然Qt已经内置了大量的信号,并且这些信号能够满足大部分的开发场景,但是Qt仍然允许开发者自定义信号&#…...
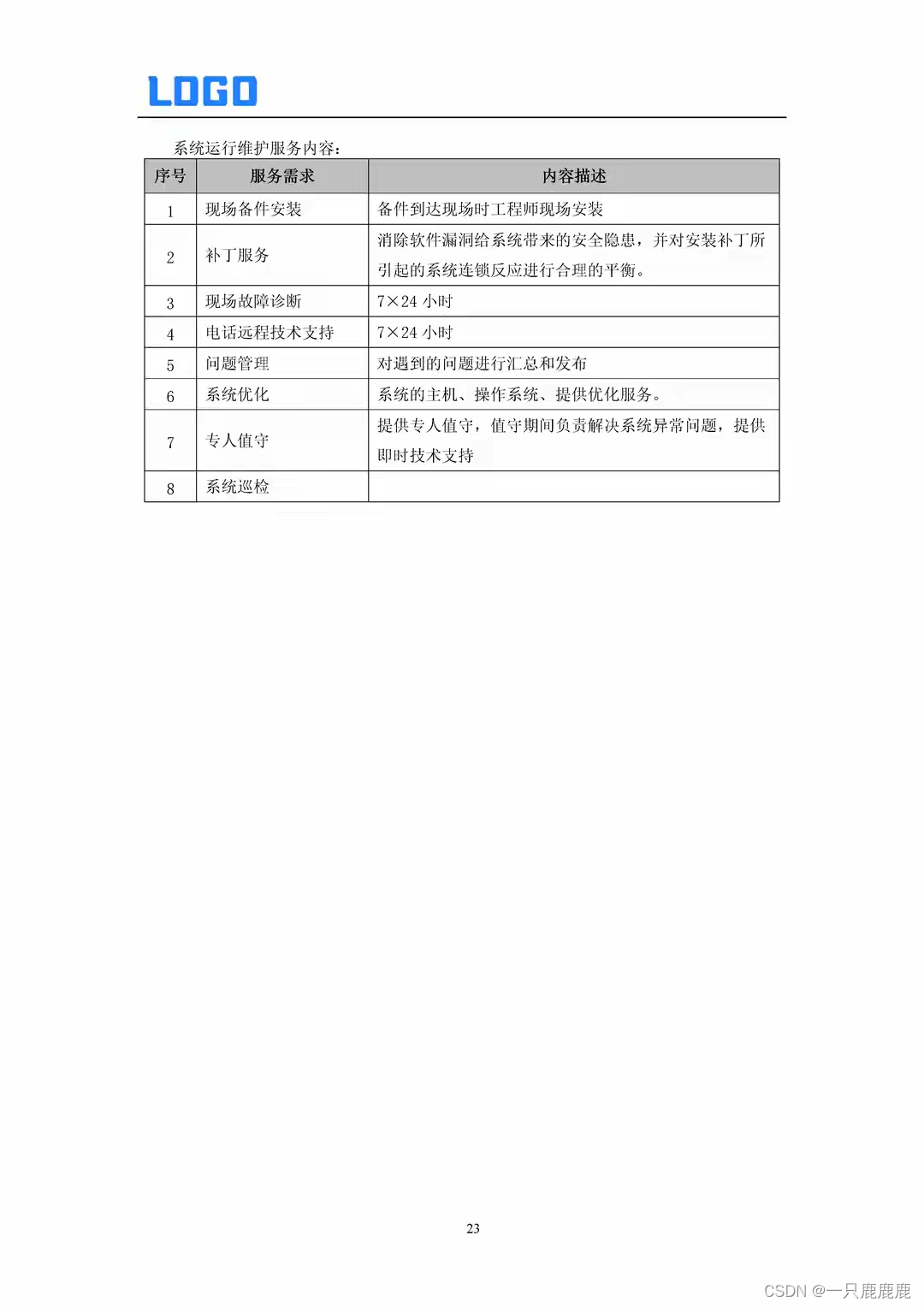
【运维方案】某系统运维需求方案参考(doc全原件2024)
系统运维需求方案 1服务目标 2服务人力需求、服务资源需求 3信息资产统计服务需求 4业务应用软件服务需求 5网络、安全系统运维服务需求 6主机、存储系统运维服务需求 7数据库系统运维服务需求 8终端运维服务需求 9综合布线系统服务需求 10大屏幕显示系统的维护需求 11视频会议…...

Linux环境使用Git同步教程
📖 前言:由于CentOS 7已于2024年06月30日停止维护,为了避免操作系统停止维护带来的影响,我们将把系统更换为Ubuntu并迁移数据,在此之前简要的学习Git的上传下载操作。 目录 🕒 1. 连接🕘 1.1 配…...

c++临时对象导致的生命周期问题
对象的生命周期是c中非常重要的概念,它直接决定了你的程序是否正确以及是否存在安全问题。 今天要说的临时变量导致的生命周期问题是非常常见的,很多时候没有一定经验甚至没法识别出来。光是我自己写、review、回答别人的问题就犯了或者看到了许许多多这…...

CSP-J 算法基础 深度优先搜索
文章目录 前言深度优先搜索通俗解释例子深度优先搜索的步骤DFS 的特点生活中的类比 为什么递归问题会变成深度优先搜索?递归与深度优先搜索的关系:递归与系统栈递归调用的过程:栈的作用: 递归与系统栈的简单示例递归实现 DFS 的简…...

LeetCode题练习与总结:基本计算器 Ⅱ--227
一、题目描述 给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。 整数除法仅保留整数部分。 你可以假设给定的表达式总是有效的。所有中间结果将在 [-2^31, 2^31 - 1] 的范围内。 注意:不允许使用任何将字符串作为数学表达式计算…...

Elasticsearch基础(七):Logstash如何开启死信队列
文章目录 Logstash如何开启死信队列 一、确保 Elasticsearch 输出插件启用 DLQ 支持 二、配置 Logstash DLQ 设置 三、查看死信队列 四、排查 CSV 到 Elasticsearch 数据量不一致的问题 Logstash如何开启死信队列 在 Logstash 中,死信队列(Dead Le…...
讲解)
c语言--力扣简单题目(链表的中间节点)讲解
题目如下: 给你单链表的头结点 head ,请你找出并返回链表的中间结点。 如果有两个中间结点,则返回第二个中间结点。 示例 1: 输入:head [1,2,3,4,5] 输出:[3,4,5] 解释:链表只有一个中间结点…...

【STM32 Blue Pill编程】-定时器计数模式
定时器计数模式 文章目录 定时器计数模式1、定时器计数模式介绍2、硬件准备及接线3、模块配置3.1 定时器计数模式配置3.2 定时器中断配置3.3 串口配置4、代码实现在本文中,我们将讨论如何在计数器模式下配置 STM32 Blue Pill 定时器模块。 要将定时器用作计数器,我们将其配置…...

【例题】lanqiao1331 二进制中 1 的个数
二进制中 1 的个数 题目描述 给定一个整数 x,输出该数二进制表示中 1 的个数。 例:9 的二进制表示为 1001,有 2 位是 1 ,所以函数返回 2。 输入描述 输入 x (内存空间为 32 位的整数)。 输出描述 第一…...

【论文解读】图像序列识别:CRNN技术在场景文本识别中的应用与突破(附论文地址)
论文地址:https://arxiv.org/pdf/1507.05717 这篇文章的标题是《An End-to-End Trainable Neural Network for Image-based Sequence Recognition and Its Application to Scene Text Recognition》,作者是Baoguang Shi, Xiang Bai和Cong Yao,…...

Vue3+CesiumJS相机定位camera
new Cesium.Camera (scene) 摄像机由位置,方向和视锥台定义。 方向与视图形成正交基准,上和右视图x上单位矢量。 视锥由6个平面定义。每个平面都由 Cartesian4 对象表示,其中x,y和z分量定义垂直于平面的单位矢量,w分量…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...
