数据结构——二叉搜索树
一、二叉搜索树概念
二叉搜索树又叫二叉排序树,它或是空树,或是具有以下性质的二叉树:
(1)若它的左子树不为空,则左子树上的所有节点的值都小于根节点的值;
(2)若它的右子树不为空,则右子树上的所有节点的值都大于根节点的值;
(3)它的左右子树也分别为二叉搜索树。
二、二叉搜索树操作
1.二叉搜索树的查找
(1)若根节点为空,则直接返回false,否则进行后续操作;
(2)如果根节点key==查找key,返回ture,否则进行后续操作;
(3)若根节点key>查找key,则在其左子树内进行查找,否则在其右子树内进行查找;
(4)递归上述过程。
2.二叉搜索树的插入
(1)若树为空,则直接插入;
(2)若树不为空,则按二叉搜索树性质查找插入位置,然后插入。
3.二叉搜索树的删除
首先查找待删除元素是否在二叉搜索树中,没有则直接返回,否则要删除的节点可分为以下四种情况:
(1)待删除节点无孩子节点;
(2)待删除节点只有左孩子;
(3)待删除节点只有右孩子;
(4)待删除节点左右孩子都有。
删除方法:
情况(1):删除方法与情况(2)和(3)相同;
情况(2):删除该节点,并使被删除节点的双亲节点指向被删除节点的左孩子节点;
情况(3):删除该节点,并使被删除节点的双亲节点指向被删除节点的右孩子;
情况(4):在它的右子树中寻找中序下的第一个节点(值最小的节点),用它的值覆盖掉被删除节点,在处理该节点的删除问题。或找它左子树中最大的节点。
三、二叉搜索的实现
1.代码实现
template<class T>
struct BSTNode {BSTNode(const T& value = T()): _left(nullptr), _right(nullptr), _value(value){}BSTNode<T>* _left;BSTNode<T>* _right;T _value;
};//约定value唯一
template<class T>
class BinarySearchTree {typedef BSTNode<T> Node;
public:BinarySearchTree(): _root(nullptr){}~BinarySearchTree() {Destroy(_root);}//插入bool Insert(const T& value) {//空树if (_root == nullptr) {_root = new Node(value);return true;}//非空Node* cur = _root;Node* parent = nullptr;//保存cur双亲节点//查找插入位置while (cur) {parent = cur;if (value < cur->_value) {cur = cur->_left;}else if (value > cur->_value) {cur = cur->_right;}else {//待插入节点已存在return false;}}//插入新节点cur = new Node(value);if (value > parent->_value) {parent->_right = cur;}else {parent->_left = cur;}return true;}//查找Node* Find(const T& value) {Node* cur = _root;while (cur) {if (value == cur->_value) {return cur;}else if (value < cur->_value) {cur = cur->_left;}else {cur = cur->_right;}}return cur;}//删除bool Erase(const T& value) {if (_root == nullptr) return false;Node* cur = _root;Node* parent = nullptr;//查找待删除节点while (cur) {//parent = cur;不能在这里记录双亲节点,因为有可能cur已经是待删除节点,会直接breakif (value == cur->_value) {break;}else if (value < cur->_value) {parent = cur;cur = cur->_left;}else {parent = cur;cur = cur->_right;}}if (cur == nullptr) return false;//没有待删除节点//删除节点if (cur->_left == nullptr) {//情况1和2if (parent == nullptr) {//是根节点且左孩子为空_root = cur->_right;}else {//不是根节点if (cur == parent->_left) parent->_left = cur->_right;else parent->_right = cur->_right;}delete cur;}else if (cur->_right == nullptr) {//情况1和3if (parent == nullptr) {//是根节点且右孩子为空_root = cur->_left;}else {//不是根节点if (cur == parent->_left) parent->_left = cur->_left;else parent->_right = cur->_left;}delete cur;}else {//情况4//查找该节点右子树最小值(或左子树的最大值)Node* prev = cur;Node* node = cur->_right;while (node->_left) {prev = node;node = node->_left;}//覆盖节点值cur->_value = node->_value;//删除节点,该节点的左孩子肯定为空if (node == prev->_left) prev->_left = node->_right;else prev->_right = node->_right;delete node;}return true;}//中序遍历void InOrder() {_InOrder(_root);std::cout << std::endl;}private://中序遍历void _InOrder(Node* root) {if (root == nullptr) return;_InOrder(root->_left);std::cout << root->_value << " ";_InOrder(root->_right);}//销毁void Destroy(Node*& root) {//利用后续遍历销毁if (root == nullptr) return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}private:Node* _root;
};2.性能分析
二叉搜索树的插入、删除操作都必须先进行查找,查找效率代表了二叉搜索树的各个操作的性能。而二叉树的结构,取决于给定的序列:
(1)最优情况下:二叉搜索树为完全二叉树,其平均比较次数为;
(2)最坏情况下:二叉搜索树退化为单支树,其平均比较次数为N/2;
所以二叉搜索树的查找、插入、删除时间复杂度都是O(N)。
相关文章:
数据结构——二叉搜索树
一、二叉搜索树概念 二叉搜索树又叫二叉排序树,它或是空树,或是具有以下性质的二叉树: (1)若它的左子树不为空,则左子树上的所有节点的值都小于根节点的值; (2)若它的…...

23年5月高项学习笔记3---项目管理概述
项目是创造独特的产品、服务或成果而进行的临时性的工作 独特:每个项目都不一样 可交付成果:某一过程,阶段或项目完成时形成的独特的并且可验证的产品、服务或成果。 临时的:明确的起点和终点、 -------- 项目集: 相…...

【组织架构】中国铁路成都局集团有限公司
0 参考 中国铁路成都局集团有限公司 1 公司介绍 中国铁路成都局集团有限公司,是中国国家铁路集团有限公司管理的18个铁路局集团有限公司之一,简称“成局”,地处中国西南,管辖范围辐射四川、贵州、重庆地区。管内地形复杂&#x…...

剧前爆米花--爪哇岛寻宝】java多线程案例——单例模式、阻塞队列及生产者消费者模型、定时器、线程池
作者:困了电视剧 专栏:《JavaEE初阶》 文章分布:这是关于java多线程案例的文章,进行了对单例模式、阻塞队列及生产者消费者模型、定时器和线程池的讲解,希望对你有所帮助! 目录 单例模式 懒汉模式实现 饿…...

Guitar Pro8中文版更新说明及系统要求介绍
Guitar Pro吉他软件是初学作曲,特别是同时又初学吉他的朋友们的良师益友,是一款极佳的初级软件,是非实时作曲软件之中的一件佳作。Guitar Pro在吉他和弦、把位的显示、推算、查询、调用等方面,也异常方便、简洁、直观和浩瀚&#…...

【id:19】【20分】A. 三数论大小(引用)
题目描述 输入三个整数,然后按照从大到小的顺序输出数值。 要求:定义一个函数,无返回值,函数参数是三个整数参数的引用,例如int &a, int &b, int &c。在函数内对三个参数进行排序。主函数调用这个函数进行…...
)
To_Heart—总结——FWT(快速沃尔什变换)
目录闲话拿来求什么或与异或闲话 这个比FFT简单了很多呢,,大概是我可以学懂的水平! 好像是叫 快速沃尔什变换 ? 拿来求什么 以 FFT 来类比。我们 FFT 可以在 O(nlogn)\mathrm{O(nlogn)}O(nlogn) 的复杂度下实现求解࿱…...

Google巨大漏洞让Win10、11翻车,小姐姐马赛克白打了
早年间电脑截图这项技能未被大多数人掌握时,许多人应该都使用过手机拍屏幕这个原始的方式。 但由于较低的画面质量极其影响其他用户的观感,常常受到大家的调侃。 但到了 Win10、11 ,预装的截图工具让门槛大幅降低。 WinShiftS 就能快速打开…...
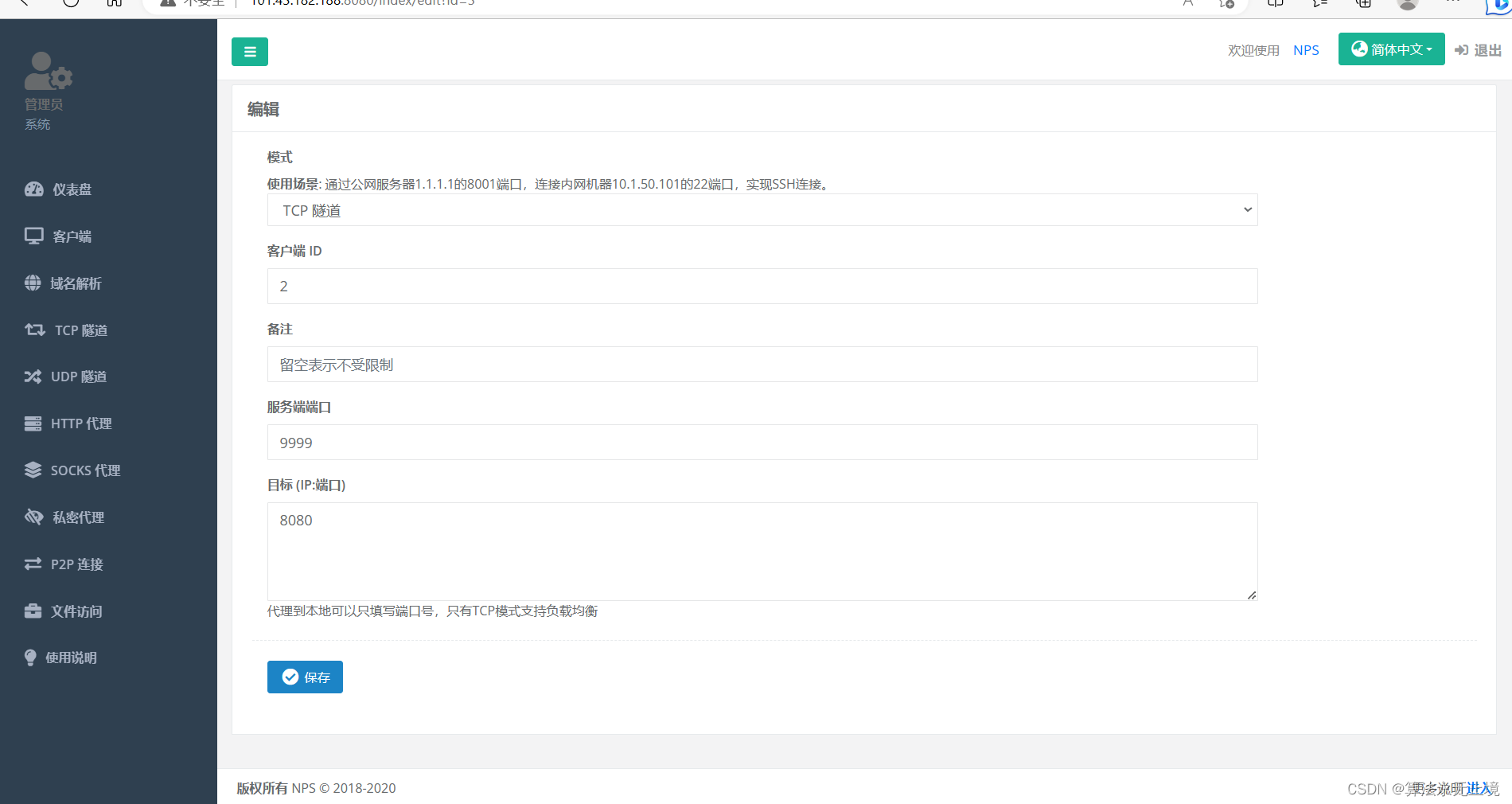
腾讯云服务器部署内网穿透(让其他人在不同ip可以访问我们localhost端口的主机项目)(nps开源项目)
首先打开shell连接我们的云服务器 然后我们再opt目录下面创建一个文件夹用来存放我们的压缩包和文件 mkdir /opt/nps 这个是它官方的安装图解.所以我们按照这个docker安装过程来: 然后我们用docker安装镜像.这样的话比较简单一点 docker pull ffdfgdfg/nps 然后我们查看docker…...

IDS、恶意软件、免杀技术、反病毒技术、APT、对称加密、非对称加密以及SSL的工作过程的技术介绍
IDS的简单介绍IDS是:入侵检测系统(intrusion detection system,简称“IDS”)是一种对网络传输进行即时监视,在发现可疑传输时发出警报或者采取主动反应措施的网络安全设备。它与其他网络安全设备的不同之处便在于&…...
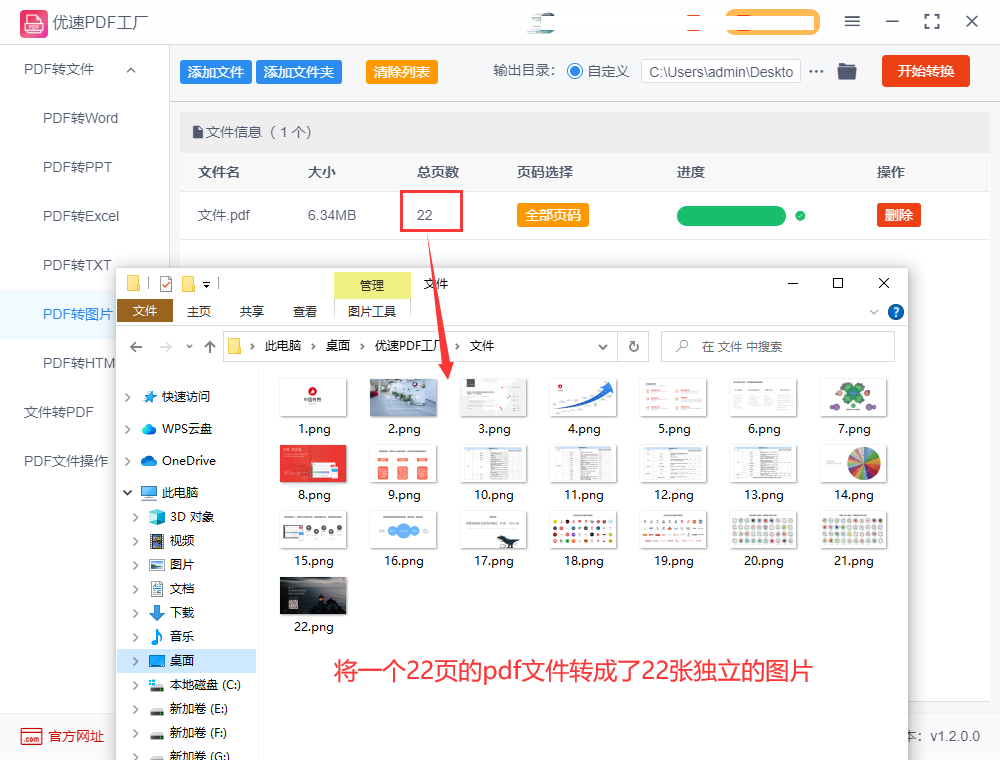
怎么把pdf转换成高清图片
怎么把pdf转换成高清图片?可以使用以下两种方法: 方法一:使用Adobe Acrobat Pro DC 1、打开需要转换的PDF文件,点击“文件”菜单中的“导出为”,在弹出的菜单中选择“图像”,然后选择“JPEG”。 2、在“…...
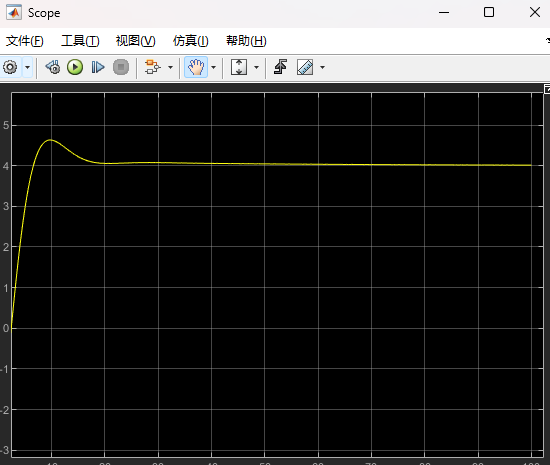
MATLAB 系统辨识 + PID 自动调参
系统辨识 PID 自动调参 文章目录系统辨识 PID 自动调参1. 导入数据1.1 从 Excel 中导入数据2. 系统辨识3. PID 自动调参1. 导入数据 1.1 从 Excel 中导入数据 如果不是从Excel中导入可以跳过该步骤 导入函数: [num,txt,raw]xlsread(xxx\xxx.xlsx);num返回的是…...

【vue3】组合式API之setup()介绍与reactive()函数的使用·上
>😉博主:初映CY的前说(前端领域) ,📒本文核心:setup()概念、 reactive()的使用 【前言】vue3作为vue2的升级版,有着很多的新特性,其中就包括了组合式API,也就是是 Composition API。学习组合…...

爬虫Day3 csv和bs4
爬虫Day3 csv和bs4 一、CSV的读和写 1. 什么是csv文件 csv文件叫做:逗号分隔值文件,像Excel文件一样以行列的形式保存数据,保存数据的时候同一行的多列数据用逗号隔开。 2. csv文件的读写操作 1) csv文件读操作 from csv import reader…...
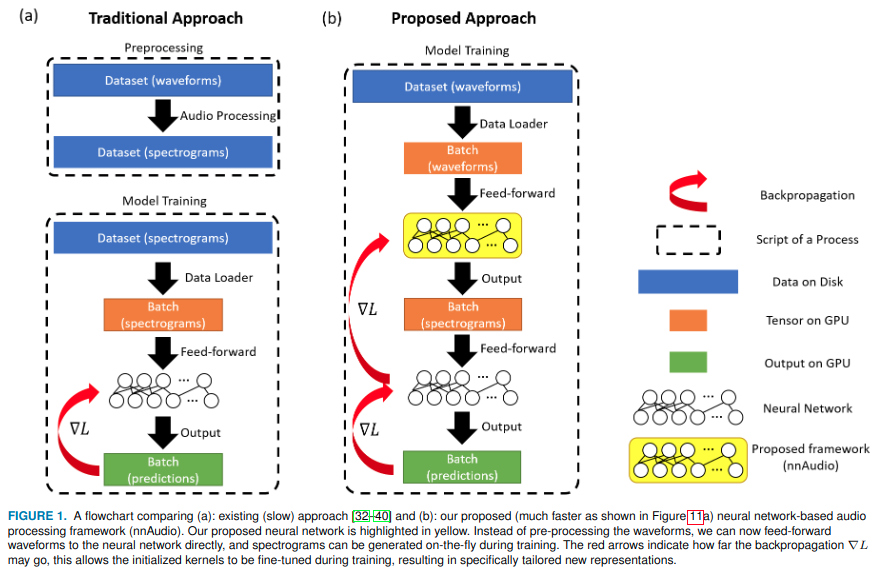
nnAudio的简单介绍
官方实现 https://github.com/KinWaiCheuk/nnAudio; 论文实现: nnAudio: An on-the-Fly GPU Audio to Spectrogram Conversion Toolbox Using 1D Convolutional Neural Networks; 以下先对文章解读: abstract 在本文中&#x…...
)
【id:134】【20分】B. 求最大值最小值(引用)
题目描述 编写函数void find(int *num,int n,int &minIndex,int &maxIndex),求数组num(元素为num[0],num[1],...,num[n-1])中取最小值、最大值的元素下标minIndex,maxIndex(若有相同最值࿰…...

Java 面向对象
一、Java 8 增强的包装类 Java是面向对象的编程语言,但它也包含了8种基本数据类型,这8种基本数据类型不支持面向对象的编程机制,基本数据类型的数据也不具备对象的特性。(没有成员变量、方法可以被调用)。Java之所以提…...
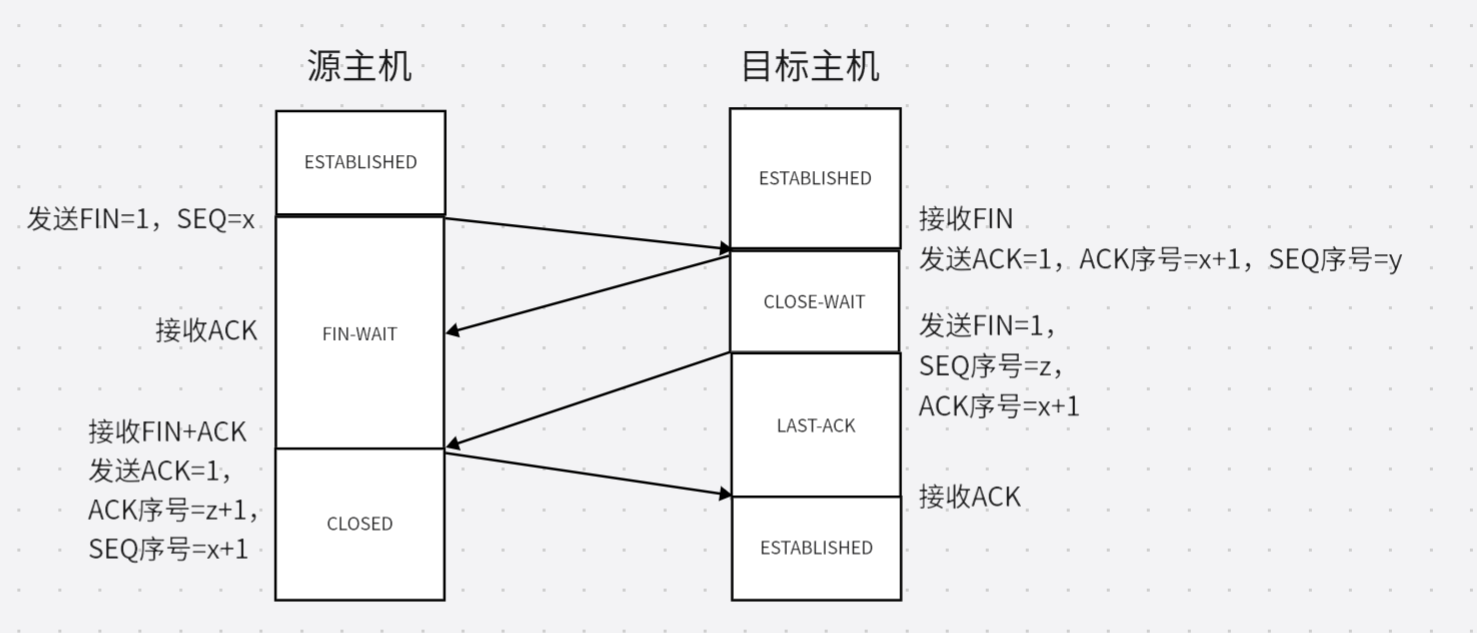
五、传输层
(一)TCP传输控制协议 可靠的、面向连接的字节流服务,全双工,有端口寻址功能 1、TCP的三种机制 1.使用序号对分段的数据进行标记,便于调整数据包 2.TCP使用确认、校验和和定时器系统提供可靠性 3.TCP使用可变大小的…...

Thinkphp 6.0一对一关联查询
本节课我们来了解关联模型中,一对一关联查询的使用方法。 一.hasOne 模式 1. hasOne 模式,适合主表关联附表,具体设置方式如下: hasOne(关联模型,[外键,主键]); return $this->hasOne(Profile::class,user_id, id); 关联模型&…...
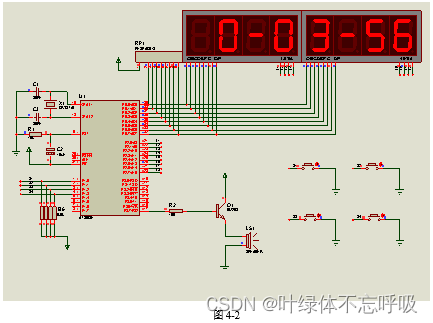
基于51单片机的自动打铃打鸣作息报时系统AT89C51数码管三极管时钟电路
wx供重浩:创享日记 对话框发送:单片机打铃 获取完整无水印论文报告说明(含源码程序、电路原理图和仿真图) 本次设计中的LED数码管电子时钟电路采用24小时制记时方式,本次设计采用AT89C51单片机的扩展芯片和6个PNP三极管做驱动&…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...
