OpenCV结构分析与形状描述符(17)判断轮廓是否为凸多边形的函数isContourConvex()的使用
- 操作系统:ubuntu22.04
- OpenCV版本:OpenCV4.9
- IDE:Visual Studio Code
- 编程语言:C++11
算法描述
测试轮廓的凸性。
该函数测试输入的轮廓是否为凸的。轮廓必须是简单的,即没有自相交。否则,函数的输出是不确定的。
cv::isContourConvex 函数是 OpenCV 提供的一个用于判断轮廓是否为凸多边形的函数。这个函数可以用来验证一个给定的轮廓是否是凸的,这对于后续处理(如使用 intersectConvexConvex 来寻找两个凸多边形的交集)是非常有用的。
函数原型
bool cv::isContourConvex
(InputArray contour
)
参数
- 参数contour 输入的二维点向量,存储在 std::vector<> 或 Mat 中
代码示例
#include <iostream>
#include <opencv2/opencv.hpp>int main()
{// 定义两个矩形的顶点cv::Mat p1 = ( cv::Mat_< float >( 4, 2 ) << 0, 0, // 左上角2, 0, // 右上角2, 2, // 右下角0, 2 ); // 左下角cv::Mat p2 = ( cv::Mat_< float >( 4, 2 ) << 1, 1, // 左上角3, 1, // 右上角3, 3, // 右下角1, 3 ); // 左下角// 验证轮廓是否为凸多边形bool isP1Convex = cv::isContourConvex( p1 );bool isP2Convex = cv::isContourConvex( p2 );std::cout << "Polygon p1 is convex: " << std::boolalpha << isP1Convex << std::endl;std::cout << "Polygon p2 is convex: " << std::boolalpha << isP2Convex << std::endl;// 如果两个多边形都是凸的,才继续进行交集计算if ( isP1Convex && isP2Convex ){cv::Mat p12;bool intersect = cv::intersectConvexConvex( p1, p2, p12, true );if ( intersect ){std::cout << "Polygons intersect." << std::endl;std::cout << "Intersection vertices:" << std::endl;for ( int i = 0; i < p12.rows; ++i ){cv::Point2f pt = p12.at< cv::Point2f >( i );std::cout << "Vertex " << i << ": (" << pt.x << ", " << pt.y << ")" << std::endl;}}else{std::cout << "Polygons do not intersect." << std::endl;}}else{std::cout << "One or both polygons are not convex." << std::endl;}return 0;
}
运行结果
Polygon p1 is convex: true
Polygon p2 is convex: true
Polygons intersect.
Intersection vertices:
Vertex 0: (2, 1)
Vertex 1: (2, 2)
Vertex 2: (1, 2)
Vertex 3: (1, 1)相关文章:
判断轮廓是否为凸多边形的函数isContourConvex()的使用)
OpenCV结构分析与形状描述符(17)判断轮廓是否为凸多边形的函数isContourConvex()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 测试轮廓的凸性。 该函数测试输入的轮廓是否为凸的。轮廓必须是简单的,即没有自相交。否则,函数的输出是不确定的。 cv:…...
P5425 [USACO19OPEN] I Would Walk 500 Miles G
*原题链接* 很离谱的题。首先可以想到暴力连边,整个图为一个完全图,将所有的边选出来,然后从小到大一条条加入,当剩下集合数量 <K 的时候就结束。答案为加入的最后一条边的大小。如果用prim算法的话时间复杂度为。足以通过此题…...

Java高级Day41-反射入门
115.反射 反射机制 1.根据配置文件re.properties指定信息,创建Cat对象并调用hi方法 SuppressWarnings({"all"}) public class ReflectionQuestion {public static void main(String[] args) throws IOException {//根据配置文件 re.properties 指定信息…...

在Linux系统上使用Docker部署java项目
一.使用Docker部署的好处: 在Linux系统上使用Docker部署项目通常会大大简化部署流程,因为Docker可以将应用程序及其依赖打包到一个独立的容器中。 Docker打包应用程序时会将其与所有依赖项(操作系统、库等)一起打包。这样&#…...

【C++】标准库IO查漏补缺
【C】标准库 IO 查漏补缺 文章目录 系统I/O1. 概述2. cout 与 cerr3. cerr 和 clog4. 缓冲区5. 与 printf 的比较 系统I/O 1. 概述 标准库提供的 IO 接口,包含在 iostream 文件中 输入流: cin输出流:cout / cerr / clog。 输入流只有一个 cin&#x…...

python简单易懂的lxml读取HTML节点及常用操作方法
python简单易懂的lxml读取HTML节点及常用操作方法 1. 初始化和基本概念 lxml 是一个强大的pyth库,用于处理XML和HTML文档。它提供了类似BeautifulSoup的功能,但性能更高。在使用lxml时,通常会先解析HTML或XML文档,得到一个Eleme…...

Java | Leetcode Java题解之第406题根据身高重建队列
题目: 题解: class Solution {public int[][] reconstructQueue(int[][] people) {Arrays.sort(people, new Comparator<int[]>() {public int compare(int[] person1, int[] person2) {if (person1[0] ! person2[0]) {return person2[0] - perso…...

安卓获取apk的公钥,用于申请app备案等
要申请app的icp备案等场景,需要app的 证书MD5指纹和公钥,示例如下: 步骤1:使用keytool从APK中提取证书 1. 打开命令行,cd 到你的apk目录,如:app/release 2. 解压APK文件: unzip yo…...
【leetcode_python】杨辉三角
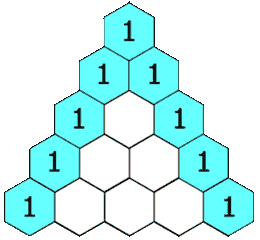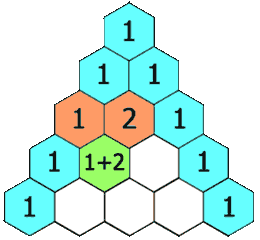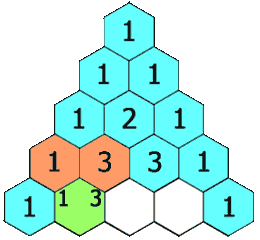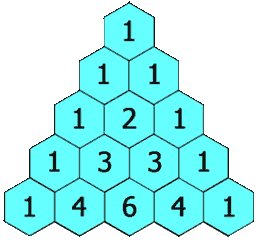
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。 在「杨辉三角」中,每个数是它左上方和右上方的数的和。 示例 1: 输入: numRows 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]示例 2: 输入: numRows 1 输出: [[1]] 方案&#…...

Parallels Desktop 20 for Mac中文版发布了?会哪些新功能
Parallels Desktop 20 for Mac 正式发布,完全支持 macOS Sequoia 和 Windows 11 24H2,并且在企业版中引入了全新的管理门户。 据介绍,新版本针对 Windows、macOS 和 Linux 虚拟机进行了大量更新,最大的亮点是全新推出的 Parallels…...

SpringBoot整合SSE-灵活管控连接
SpringBoot整合SSE(管控连接) 1、sse单向通信整成逻辑双向通信。 2、轻量级实现端对端信息互通。 3、避免繁琐配置学习。 核心点通过记录连接码和心跳检测实现伪双向通道,避免无效连接占用过多内存。 服务器推送(Server Push)技术允许网站和应用在有新内容可用时主动向用户…...

挖矿木马-Linux
目录 介绍步骤 介绍 1、挖矿木马靶机中切换至root用户执行/root目录下的start.sh和attack.sh 2、题目服务器中包含两个应用场景,redis服务和hpMyAdmin服务,黑客分别通过两场景进行入侵,入侵与后续利用线路路如下: redis服务&…...

【leetcode——415场周赛】——python前两题
3289. 数字小镇中的捣蛋鬼 数字小镇 Digitville 中,存在一个数字列表 nums,其中包含从 0 到 n - 1 的整数。每个数字本应 只出现一次,然而,有 两个 顽皮的数字额外多出现了一次,使得列表变得比正常情况下更长。 为了…...

【CSS in Depth 2 精译_029】5.2 Grid 网格布局中的网格结构剖析(上)
当前内容所在位置(可进入专栏查看其他译好的章节内容) 第一章 层叠、优先级与继承(已完结) 1.1 层叠1.2 继承1.3 特殊值1.4 简写属性1.5 CSS 渐进式增强技术1.6 本章小结 第二章 相对单位(已完结) 2.1 相对…...
 TCP函数学习)
ZYNQ LWIP(RAW API) TCP函数学习
1 LWIP TCP函数学习 tcp_new()–新建控制块 这个函数用于分配一个TCP控制块,它通过tcp_alloc()函数分配一个TCP控制块结构来存储TCP控制块的数据信息, 如果没有足够的内容分配空间,那么tcp_alloc()函数就会尝试释放一些不太重要的TCP控制块, 比如就会释放处于TIME_WAIT、C…...

Spring Boot,在应用程序启动后执行某些 SQL 语句
在 Spring Boot 中,如果你想在应用程序启动后执行某些 SQL 语句,可以利用 spring.sql.init 属性来配置初始化脚本。这通常用于在应用启动时创建数据库表、索引、视图等,或者填充默认数据。data-locations 和 schema-locations 指定了 SQL 脚本…...

【SQL】百题计划:SQL最基本的判断和查询。
[SQL]百题计划 Select product_id from Products where low_fats "Y" and recyclable "Y";...

04_Python数据类型_列表
Python的基础数据类型 数值类型:整数、浮点数、复数、布尔字符串容器类型:列表、元祖、字典、集合 列表 列表(List)是一种非常灵活的数据类型,它可以用来存储一系列的元素。容器类型,能够存储多个元素的…...

F5设备绑定EIP
公网IP 公网IP(Public IP Address)是指可以直接在互联网上访问的IP地址,用于标识网络上的设备或主机。它允许外部网络访问您的云服务器,如提供远程登录服务、访问Web服务器等。然而,这并不意味着公网IP不需要路由。 …...

使用 PyCharm 新建 Python 项目详解
使用 PyCharm 新建 Python 项目详解 文章目录 使用 PyCharm 新建 Python 项目详解一 新建 Python 项目二 配置环境1 项目存放目录2 Python Interpreter 选择3 创建隔离环境4 选择你的 Python 版本5 选择 Conda executable 三 New Window 打开项目四 目录结构五 程序编写运行六 …...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
