树数据结构
什么是树数据结构?
树数据结构是一种层次结构,用于以易于导航和搜索的方式表示和组织数据。它是由边连接的节点集合,节点之间具有层次关系。树的最顶端的节点称为根,它下面的节点称为子节点。每个节点可以有多个子节点,这些子节点也可以有自己的子节点,形成递归结构。
这种数据结构是在计算机中组织和存储数据以便更有效地使用的专门方法。它由中心节点、结构节点和子节点组成,它们通过边连接。我们也可以说树数据结构具有相互连接的根、枝和叶。

树入门——数据结构与算法教程
递归定义:
一棵树由一个根和零个或多个子树 T 1 , T 2 , … , T k组成,这样从树的根到每个子树的根都有一条边。

为什么 Tree 被认为是非线性数据结构?
树中的数据不是按顺序存储的,即它们不是线性存储的。相反,它们被安排在多个层次上,或者我们可以说它是一个层次结构。因此,树被认为是一种非线性数据结构。
树数据结构中的基本术语:
- 父节点:节点的前身节点称为该节点的父节点。{B}是{D, E}的父节点。
- 子节点:节点的直接后继节点称为该节点的子节点。例子:{D, E}是{B}的子节点。
- 根节点:树的最顶端节点或没有任何父节点的节点称为根节点。{A }是树的根节点。一棵非空树必须恰好包含一个根节点和从根到树的所有其他节点的恰好一条路径。
- 叶节点或外部节点:没有任何子节点的节点称为叶节点。{K, L, M, N, O, P}是树的叶节点。
- 节点的祖先:根节点到该节点的路径上的任何前任节点称为该节点的祖先。{A,B}是节点{E}的祖先节点
- 后代:从叶节点到该节点的路径上的任何后继节点。{E,I}是节点 {B} 的后代。
- 兄弟节点:同一个父节点的子节点称为兄弟节点。{D,E}称为兄弟姐妹。
- 节点级别:从根节点到该节点的路径上的边数。根节点的级别为0。
- 内部节点:至少有一个子节点的节点称为内部节点。
- 节点的邻居:该节点的父节点或子节点称为该节点的邻居。
- 子树:树的任何节点及其后代。
树的属性:
- 边数:边可以定义为两个节点之间的连接。如果一棵树有 N 个节点,那么它将有 (N-1) 条边。从每个节点到树的任何其他节点只有一条路径。
- 节点深度:节点深度定义为从根节点到该节点的路径长度。每条边为路径增加 1 个长度单位。因此,它也可以定义为从树的根到节点的路径中的边数。
- 节点的高度:节点的高度可以定义为从该节点到树的叶节点的最长路径的长度。
- 树的高度:树的高度是从树的根到树的叶节点的最长路径的长度。
- 节点的度:连接到该节点的子树的总数称为该节点的度。叶节点的度数必须为0。树的度是树中所有节点中节点的最大度。
还有一些属性是:
- 在树中遍历是通过深度优先搜索和广度优先搜索算法完成的。
- 它没有回路也没有电路
- 它没有自循环
- 它的层次模型。
句法:
struct Node
{
int data;
struct Node *left_child;
struct Node *right_child;
};
树的基本操作:
创建——在数据结构中创建一棵树。
Insert - 在树中插入数据。
Search - 在树中搜索特定数据以检查它是否存在。
Preorder Traversal – 在数据结构中以预序方式执行树的遍历。
In order Traversal——按顺序遍历树。
后序遍历——以后序方式执行树的遍历。
树数据结构示例

这里,
节点1是根节点
1 是 2 和 3 的父级
2和3是兄弟姐妹
4、5、6、7为叶节点
1和2是5的祖先
// C++ program to demonstrate some of the above
// terminologies
#include <bits/stdc++.h>
using namespace std;
// Function to add an edge between vertices x and y
void addEdge(int x, int y, vector<vector<int> >& adj)
{adj[x].push_back(y);adj[y].push_back(x);
}
// Function to print the parent of each node
void printParents(int node, vector<vector<int> >& adj,int parent)
{// current node is Root, thus, has no parentif (parent == 0)cout << node << "->Root" << endl;elsecout << node << "->" << parent << endl;// Using DFSfor (auto cur : adj[node])if (cur != parent)printParents(cur, adj, node);
}
// Function to print the children of each node
void printChildren(int Root, vector<vector<int> >& adj)
{// Queue for the BFSqueue<int> q;// pushing the rootq.push(Root);// visit array to keep track of nodes that have been// visitedint vis[adj.size()] = { 0 };// BFSwhile (!q.empty()) {int node = q.front();q.pop();vis[node] = 1;cout << node << "-> ";for (auto cur : adj[node])if (vis[cur] == 0) {cout << cur << " ";q.push(cur);}cout << endl;}
}
// Function to print the leaf nodes
void printLeafNodes(int Root, vector<vector<int> >& adj)
{// Leaf nodes have only one edge and are not the rootfor (int i = 1; i < adj.size(); i++)if (adj[i].size() == 1 && i != Root)cout << i << " ";cout << endl;
}
// Function to print the degrees of each node
void printDegrees(int Root, vector<vector<int> >& adj)
{for (int i = 1; i < adj.size(); i++) {cout << i << ": ";// Root has no parent, thus, its degree is equal to// the edges it is connected toif (i == Root)cout << adj[i].size() << endl;elsecout << adj[i].size() - 1 << endl;}
}
// Driver code
int main()
{// Number of nodesint N = 7, Root = 1;// Adjacency list to store the treevector<vector<int> > adj(N + 1, vector<int>());// Creating the treeaddEdge(1, 2, adj);addEdge(1, 3, adj);addEdge(1, 4, adj);addEdge(2, 5, adj);addEdge(2, 6, adj);addEdge(4, 7, adj);// Printing the parents of each nodecout << "The parents of each node are:" << endl;printParents(Root, adj, 0);// Printing the children of each nodecout << "The children of each node are:" << endl;printChildren(Root, adj);// Printing the leaf nodes in the treecout << "The leaf nodes of the tree are:" << endl;printLeafNodes(Root, adj);// Printing the degrees of each nodecout << "The degrees of each node are:" << endl;printDegrees(Root, adj);return 0;
}
The parents of each node are: 1->Root 2->1 5->2 6->2 3->1 4->1 7->4 The children of each node are: 1-> 2 3 4 2-> 5 6 3-> 4-> 7 5-> 6-> 7-> The leaf nodes of the tree are: 3 5 6 7 The degrees of each node are: 1: 3 2: 2 3: 0 4: 1 5: 0 6: 0 7: 0
树数据结构的类型
不同类型的树数据结构如下:
1.一般树
一般的树数据结构对节点数没有限制。这意味着父节点可以有任意数量的子节点。
2.二叉树
二叉树的一个节点最多可以有两个子节点。在给定的树图中,节点 B、D 和 F 是左孩子,而 E、C 和 G 是右孩子。
3.平衡树
如果左子树和右子树的高度相等或最多相差1,则该树称为平衡树。

4.二叉搜索树
顾名思义,二叉搜索树用于各种搜索和排序算法。示例包括 AVL 树和红黑树。它是一种非线性数据结构。它表明左节点的值小于其父节点,而右节点的值大于其父节点。
树数据结构的应用:
树型数据结构的应用如下:
1. 生成树:它是路由器中用于将数据包定向到目的地的最短路径树。
2. 二叉搜索树:它是一种树状数据结构,有助于维护已排序的数据流。
- 满二叉树
- 完全二叉树
- 偏二叉树
- 严格二叉树
- 扩展二叉树
3.分层存储数据:树型数据结构用于存储分层数据,即数据以顺序的形式排列。
4. 语法树:语法树表示程序源代码的结构,在编译器中使用。
5. Trie:它是一种快速有效的动态拼写检查方法。它还用于从集合中定位特定键。
6、堆:也是一种树型数据结构,可以用数组的形式来表示。它用于实现优先级队列。
7. 人工智能:决策树和其他基于树的模型常用于机器学习和人工智能中,以进行预测和数据分类。
8. 数据库:一些数据库使用树来组织数据以进行高效的搜索和排序。
9. 网络:网络的路由算法,例如 Internet 协议 (IP) 路由,使用树来找到数据从一个网络传输到另一个网络的最佳路径。
树数据结构的优点
- 高效的插入、删除和搜索操作。
- 树在可以存储的数据类型方面具有灵活性。
- 它用于表示层次关系。
- 它具有表示递归结构的能力。
- 用于各种算法和数据结构,如霍夫曼编码和决策树。
- 与其他数据结构(如列表和链表)相比,树使用的空间更少。
- 树木本质上是动态的。
- 树数据结构可以在添加或删除新数据时自动自组织,这可以提高性能并降低复杂性。
相关文章:

树数据结构
什么是树数据结构? 树数据结构是一种层次结构,用于以易于导航和搜索的方式表示和组织数据。它是由边连接的节点集合,节点之间具有层次关系。树的最顶端的节点称为根,它下面的节点称为子节点。每个节点可以有多个子节点,…...

Spring Boot整合Redis并提供多种实际场景的应用
Spring Boot整合Redis并提供多种实际场景的应用1. 整合Redis2. 场景应用2.1 缓存2.2 分布式锁2.3 计数器2.4 发布/订阅3. 总结Spring Boot是一个快速构建基于Spring框架的应用程序的工具,它提供了大量的自动化配置选项,可以轻松地集成各种不同的技术。Re…...
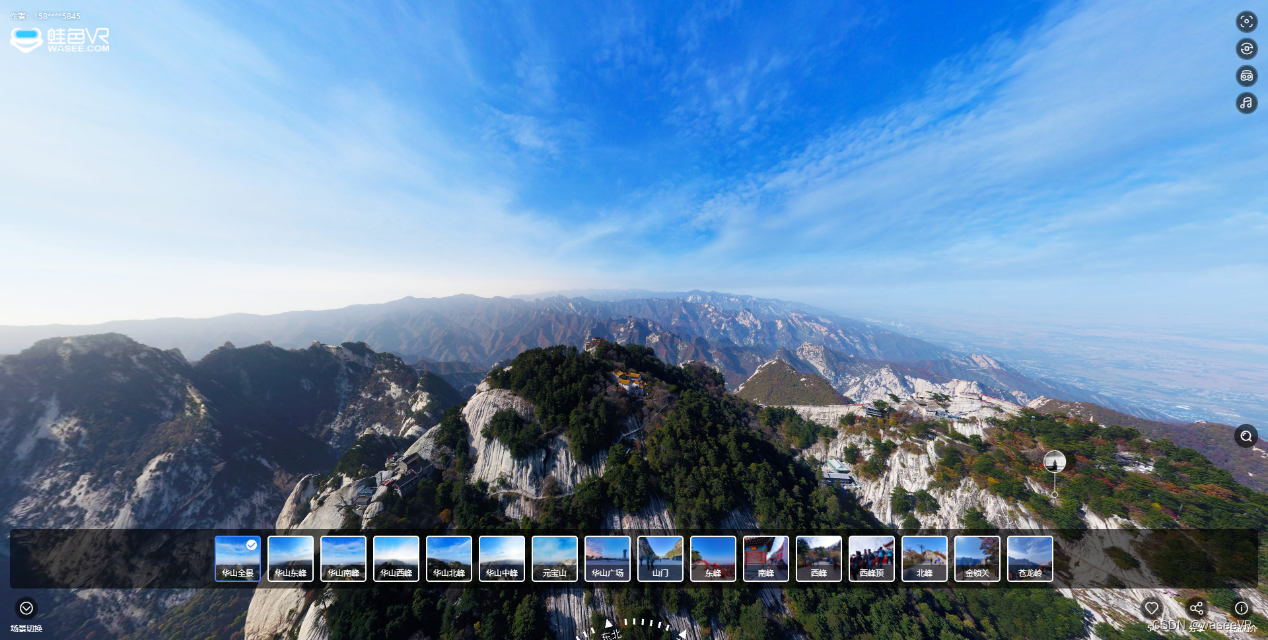
VR全景图片,助力VR全景制作,720全景效果图
VR全景图片是指通过全景相机或多相机组合拍摄全景画面,并进行拼接处理生成全景图像的过程。VR全景图片的应用范围广泛,包括旅游和景区、房地产、汽车、艺术和文化、电影和娱乐等领域。本文将详细介绍VR全景图片的类型、应用场景、市场前景和发展趋势。 一…...

Kali Linux20款重要软件
Kali Linux 是一个流行的网络安全测试平台,它包含了大量的工具和应用程序,以下是其中20款最常用的软件和工具: Metasploit:Metasploit 是一个广泛使用的漏洞评估工具,可以帮助安全专业人员测试系统中的漏洞。Aircrack…...

C语言测试五
windows是什么类型的系统(实时还是分时)?有什么区别? 分时操作系统。如果在单核的情况下,分时操作系统多个进程共用一个单核,该单核会将其执行时间分成相应的时间片,每个进程占用一定的时间片&a…...
【微服务~原始真解】Spring Cloud —— 访问数据库整合Druid数据源
🔎这里是【秒懂云原生】,关注我学习云原生不迷路 👍如果对你有帮助,给博主一个免费的点赞以示鼓励 欢迎各位🔎点赞👍评论收藏⭐️ 👀专栏介绍 【秒懂云原生】 目前主要更新微服务,…...

前端入门必刷题,经典算法—两数之和
优美的前⾔ 年轻的码农哟~ 你是不是⼀直在思考⾃我提升的问题~ 思来想去,决定从算法抓起(单押)~ 拿起⼜放下,经历过多少次放弃(单押 ✖ 2)~ 决定了!这次让我来帮你梳理(单押 ✖ 3&a…...

‘海外/国外‘地区微博签到shu据(正题在第二部分)
最近失眠,研究了项关于weibo爬虫的新功能,种种原因,大家可跳过第一部分的引用直接看第二部分。 内容来源:健康中国、生命时报、央视等 失眠标准一:3个“30分钟” ● 入睡困难,从躺下想睡到睡着间隔…...

Springboot——SB整合Mybatis的CURD(基于注解进行开发)
此处是根据需求实现基本操作 上面这里涉及到了条件分页查询,还有增加和批量删除员工信息,右边编辑就是先查询后更新操作,叫做查询回显,然后在原有基础上进行更新 环境准备 在下面的入门案例的整体环境下把数据库表换成empSpring…...

现在大专生转IT可行吗?
当然可行的。 大专也是人,为什么不可以选择喜欢的专业学习,现在大学生遍地都是,学历已经不是限制你发展的因素了。有的人就是不擅长理论学习,更喜欢技术。IT也只是一个普普通通的技术行业,跟其他技术行业一样…...

XC7A50T-1CSG324I、XC7A50T-2CSG324I Artix-7 FPGA可编程门阵列
Artix-7 FPGA能够在多个方面实现更高的性价比,这些方面包括逻辑、信号处理、嵌入式内存、LVDS I/O、内存接口,以及收发器。MicroBlaze CPU针对Xilinx FPGA进行了优化,是一种可高度配置的32位RISC处理器,可为微控制器、实时处理器和…...

linux安装图片处理软件ImageMagick
下载地址: wget https://download.imagemagick.org/archive/ImageMagick-7.1.1-4.tar.gz 或者 wget --no-check-certificate https://download.imagemagick.org/archive/ImageMagick-7.1.1-4.tar.gz 安装命令: tar -zxvf ImageMagick-7.1.1-4.tar.…...

【Java基础】JavaCore核心-反射技术
文章目录1.什么是反射技术2.反射-获取类对象方式3.反射-获取声明构造器4.反射-对象创建实战5.反射-方法和属性实战6.反射-属性值操作实战7.反射-invoke运行类方法1.什么是反射技术 Java的反射(reflection)机制是指在程序的运行状态中 可以构造任意一个类…...
)
AWGN后验估计下的均值与协方差关系(向量和标量形式)
文章目录AWGN信道向量模型后验均值与协方差的关系从实数域拓展到复数域小结AWGN信道向量模型 考虑一个随机向量x∼pX(x)\boldsymbol x \sim p_{\boldsymbol X}(\boldsymbol x)x∼pX(x),信道模型为 qxv,v∼N(0,Σ)\boldsymbol q \boldsymbol x \boldsymbol v, \…...

Linux常用命令之文件搜索命令
1、常用搜索-find 命令find英文原意find所在路径/bin/find执行权限所有用户功能描述文件搜索语法find [搜索范围] [搜索条件] (默认准确搜索)范例find /etc -name init?? 常用的搜索条件的选项包括: -name:按照文件名进行匹配查找,例&…...

ChatGPT给软件测试行业带来的可能
软件测试在软件开发过程中扮演着至关重要的角色,因为它可以确保软件的质量和可靠性。而随着人工智能技术的不断发展,ChatGPT作为一个强大的自然语言处理工具,可以在软件测试中发挥出许多重要的作用。本文将介绍ChatGPT在软件测试应用中带来的…...

Cadence Allegro 导出Properties on Nets Report报告详解
⏪《上一篇》 🏡《上级目录》 ⏩《下一篇》 目录 1,概述2,Properties on Nets Report作用3,Properties on Nets Report示例4,Properties on Nets Report导出方法4.1,方法14.2,方法2B站关注“硬小二”浏览更多演示视频...
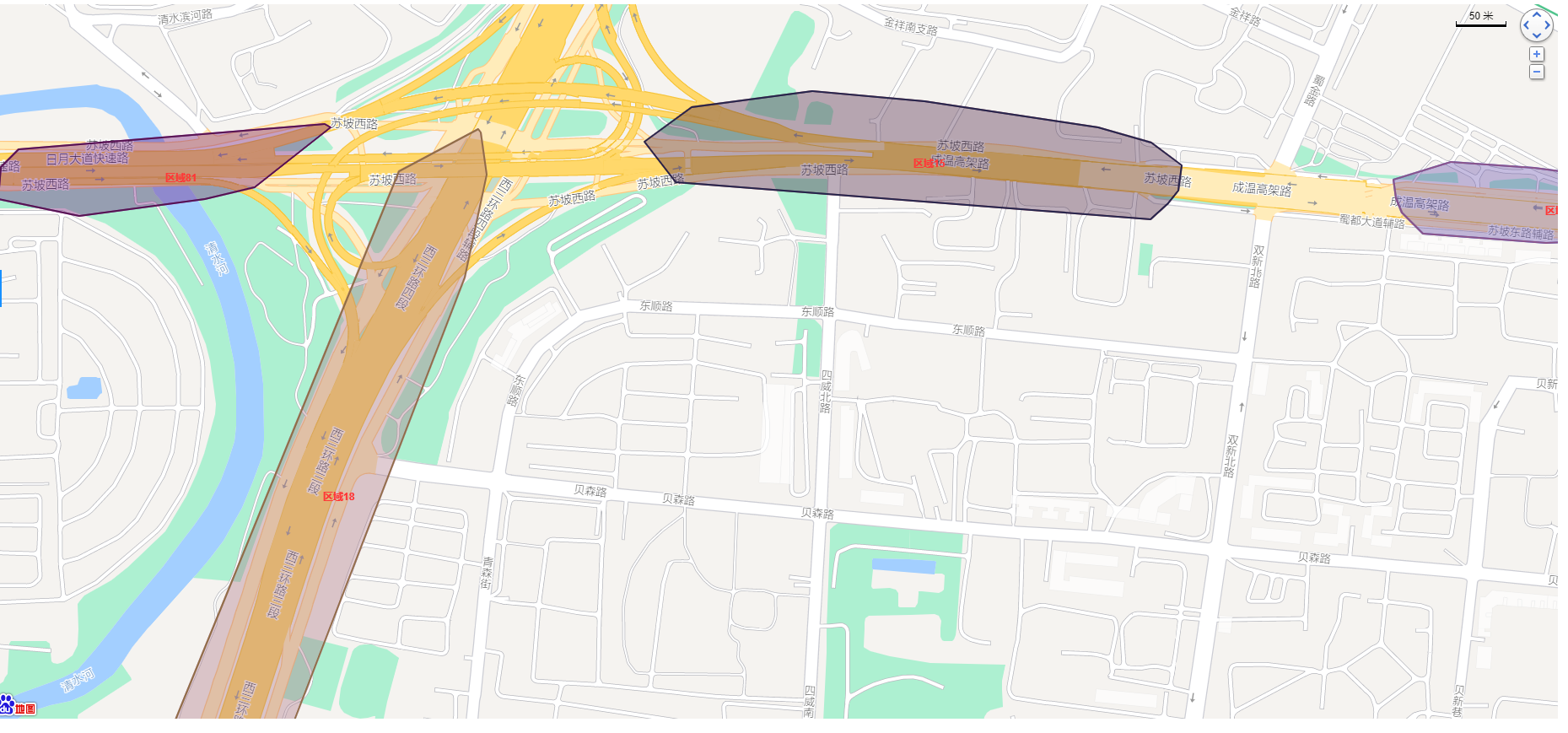
JAVA代码 实现定位数据动态聚集并绘制多边形区域
文章目录思路1、限制聚合距离2、绘制多边形区域3、多边形区域之间合并4、多边形定边点4、逻辑流程一些性能上的优化1、多边形设置圆心2、采用分支合并思路3、清理聚集较分散区域合理性处理1、解决多边形内凹角问题2、解决定边点插入位置问题3、多边形区域扩展成果展示最近有根据…...

基于储能进行调峰和频率调节研究【超线性增益的联合优化】(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

体验 Linux 的几个监控命令(htop、nmon、netdata)
体验 Linux 的几个监控命令htopnmonnetdatahtop 安装, sudo dnf install -y htop使用, htopnmon 安装, sudo dnf install -y nmon使用, nmon输入c, 输入C, 输入m, 输入n, 输入…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...
