理解对数——金融问题中的自然对数(以e为底的对数)
第3章 金融问题(Financial Matters)
——金融问题中的自然对数
If thou lend moneyto any ofMy people. ...
thou shalt not beto him as a creditor;
neither shall yelay upon him interest.
(如果你借钱给我的任何人。 ……你不应该是他的债权人;也不可向他加息。)
——EXODUS 22:24
自古以来(From timeimmemorial),金钱问题一直是人类关注的中心。生活的其他方面没有比获得财富和实现财务安全的冲动更平凡的了(mundane)。因此,在 17 世纪早期,一位匿名数学家——或者可能是商人或放债人——注意到货币增长的方式与某个数学表达式在无穷大时的行为之间存在一种奇怪的联系,这一定是令人惊讶的。
对金钱的任何考虑的概念的核心是利息(interest),或贷款支付的额外的钱。借钱收费的做法可以追溯到有文字记载的历史之初。 事实上,我们所知的许多最早的数学文献都涉及与利率相关的问题。例如,一块来自美索不达米亚(Mesopotamia)(古希腊对两河流域称谓)的黏土板(clay tablet),可追溯到公元前1700 年左右,现在存放在卢浮宫(Muséedu Louvre,法国博物馆),这块泥板提出了以下问题:如果以 20%的年复合利率投资,一笔钱需要多长时间才能翻倍?[1] 为了用代数语言来确切表达或公式化(formulate)这个问题,我们注意到每年年底总和增长 20%,即增长到原来的1.2倍;因此在x 年后总和将增长到 倍。因为问题是多久时间才能翻倍,即这等于原始总和的两倍,所以我们有
倍。因为问题是多久时间才能翻倍,即这等于原始总和的两倍,所以我们有  (注意原始总和不进入等式)。
(注意原始总和不进入等式)。
现在,我们来解这个方程,即,我们必须求得这个未知的指数——我们必须使用对数,这是巴比伦人(Babylonians)所没有的方法。无论如何,他们通过观察(译注:通过直接自乘法可得),可以求得这个指数的近似解;他们观察到, ,而
,而  ; 因此,x 一定是一个位于区间 3 到 4 之间的数(译注:小数)。为了缩窄这个待求值的所在区间,他们使用了一个称为线性插值(interpolation)的过程。求得一个将区间 3 到 4 划分开的数,使其划分比率与2 划分区间 1.728 到2.0736 相同。这就导致产生了一个以 x 为未知量的(一阶)线性方程,这个方程可以很容易地使用初等代数知识求解。但是,巴比伦人还没有我们现代的代数技巧,对于他们来说,要求得满足要求的值并不是一项简单的任务。然而,他们给出的值x = 3.7870,非常接近正确解3.8018(即,大约 3 年零 9 个月18 天)。我们应当指出,巴比伦人不使用十进制记数系统,十进制系统仅始于中古时代早期;他们采用的是60 进制(sexagesimal)记数系统,这是一种基于数60 的进制系统,满60 进位。按照60 进制的记法,卢浮宫粘土板给出的答案是3;47,13,20 ,其中,六十进制记数系统指的是 (
; 因此,x 一定是一个位于区间 3 到 4 之间的数(译注:小数)。为了缩窄这个待求值的所在区间,他们使用了一个称为线性插值(interpolation)的过程。求得一个将区间 3 到 4 划分开的数,使其划分比率与2 划分区间 1.728 到2.0736 相同。这就导致产生了一个以 x 为未知量的(一阶)线性方程,这个方程可以很容易地使用初等代数知识求解。但是,巴比伦人还没有我们现代的代数技巧,对于他们来说,要求得满足要求的值并不是一项简单的任务。然而,他们给出的值x = 3.7870,非常接近正确解3.8018(即,大约 3 年零 9 个月18 天)。我们应当指出,巴比伦人不使用十进制记数系统,十进制系统仅始于中古时代早期;他们采用的是60 进制(sexagesimal)记数系统,这是一种基于数60 的进制系统,满60 进位。按照60 进制的记法,卢浮宫粘土板给出的答案是3;47,13,20 ,其中,六十进制记数系统指的是 (  ),或者是一个非常接近3.7870 的数。[2]
),或者是一个非常接近3.7870 的数。[2]
在某种程度上,巴马伦人确实使用了某种对数表。在现存的粘土板中,某些板列出了数 1/36,1/16,9,和 16 (前两个以六十进制系统表示为 0; 1,40 和 0;3,4)的前十个幂——所有都是完全平方。由于这样的表列出了一个数的幂而不是指数,所以除了巴比伦人没有使用单一的标准底数来表示他们的幂之外,它实际上是一张反对数表。这些表似乎是为了处理涉及复利的特定问题而不是为了一般用途而编制的。[3]
我们简单考察一下这个复利是如何执行的。假设我们在支付 5% 年利息的账户中投资 100 美元(“本金(principal)”),每年复利。一年结束时,我们的余额将为100 x 1.05 = 105美元。然后,银行会将这笔新金额视为恰好以相同利率进行再投资的新本金。因此,在第二年末,余额将为 105 x 1.05 = 110.25 美元,在第三年末余额为 110.25x 1.05=115.76 美元,依此类推。(因此,不仅本金享有年息,前面本金之上的利息也享有利息——因此称为“复利”。) 我们看到我们的余额以等比级数(geometric progression)增长,通比(或称公比)(commonratio)为 1.05。 相比之下,在支付单利(simpleinterest)的账户中,年利率仅适用于原始本金(originalprincipal),因此每年产生的利息都相同。如果我们以 5% 的单利投资 100 美元,我们的余额每年会增加 5 美元,这时,我们的本息呈现为等差级数(arithmeticprogression) 100,105,110,115,依此类推。显然,无论利率如何,以复利投资的资金最终将比以单利投资增长得更快。
从这个例子中很容易看出一般情况下会发生什么。假设我们将 P 美元的本金投资于一个支付 r % 年复利利率的账户(在计算中我们总是将 r 表示为小数,例如,表示为0.05 而不是5% )。这意味着在第一年末我们的余额将为P (1 + r),第二年末我们的余额将为  ,依此类推,则t 年后余额将变成
,依此类推,则t 年后余额将变成  。用S 表示这个余额,我们得出公式
。用S 表示这个余额,我们得出公式
 ---------------------------------------------------(1)
---------------------------------------------------(1)
这个公式几乎是所有财务计算的基础,无论它们适用于银行账户、贷款、抵押贷款(mortgages)还是年金(annuities)。有些银行计算应计利息不是一次,而是一年计算数次。例如,如果 5% 的年利率每半年复利一次,则银行将使用年利率的二分之一作为每期利率。 因此,在一年内,100 美元的本金将复利两次,每次的利率为 2.5% ;这将达到  或 105.0625 美元,如果年复合利率为 5%,则比相同本金的收益率高出约 6 美分。
或 105.0625 美元,如果年复合利率为 5%,则比相同本金的收益率高出约 6 美分。
在银行业,人们会发现各种各样的复利计划——每年、每半年、每季度、每周甚至每天。假设复利每年进行 n 次。对于每个“转换期(conversionperiod)”,银行使用年利率除以 n,即  。 由于在 t 年内有 (nt ) 个转换期,本金 P 将在 t 年后产生金额
。 由于在 t 年内有 (nt ) 个转换期,本金 P 将在 t 年后产生金额
 ---------------------------------------------------(2)
---------------------------------------------------(2)
显然,方程(1)仅仅是方程(2)的一个特例——当 n = 1 时的情况。
假设年利率相同,比较给定本金在不同转换期一年后将产生的金额将很有趣。让我们以 P = 100 美元 和 r = 5% = 0.05为例加以说明。在这里,会用到手持计算器。如果计算器有求幂键(通常用符号  表示),我们可以直接用它来讲算期望的值;此外,我们必须重复乘以因式(1 + 0.05/ n)。结果如表 3.1 所示,非常令人惊讶。 正如我们所见,100 美元的本金每日复利收益率仅比年复利高13美分,比月复利或周复利高约1美分!我们把钱投资在哪个账户上几乎没有什么区别。[4]
表示),我们可以直接用它来讲算期望的值;此外,我们必须重复乘以因式(1 + 0.05/ n)。结果如表 3.1 所示,非常令人惊讶。 正如我们所见,100 美元的本金每日复利收益率仅比年复利高13美分,比月复利或周复利高约1美分!我们把钱投资在哪个账户上几乎没有什么区别。[4]
------------表3.1 100 美元在不同转换期以5%的年利率投资一年的余额--------------

(译注:Semiannually-按半年期,quarterly-按季度)
为了进一步探讨这个问题,让我们考虑方程(2)的一个特例,即 r = 1 的情况。这意味着年利率为 100% ,而且肯定没有哪家银行提供过如此慷慨的报价。然而,我们想到的不是实际情况,而是一个具有深远数学结果的假设案例。为了简化我们的讨论,让我们假设P = 1 美元和 t = 1 年(译注:在这个表达式中,P 取多少并不影响表达式的性质,因此,为方便记,取P = 1;同时,t 的取值也不影响表达式的性质,为方便记,取 t = 1;而对于 r 的取值情况,对于某个常数来讲,当 n 趋于无穷大时, 与
与  呈现出来性质是一样的,因此只需分析 r = 1这种情况即可)。 方程(2)则变为
呈现出来性质是一样的,因此只需分析 r = 1这种情况即可)。 方程(2)则变为
 ---------------------------------------------------(3)
---------------------------------------------------(3)
我们的目标是研究这个公式在增加 n 值时的行为。结果在表 3.2 中给出。
--------------------表3.2  随n 变化的取值-------------------
随n 变化的取值-------------------

看起来 n 的任何进一步增加都几乎不会影响结果——变化将发生在越来越不重要的数字上。
但是,这种模式会一直随着n 的增大而保持不变吗?是否有可能无论n 有多大, 的值都将稳定在 2.71828 附近?详细的数学分析确实证实了这种有趣的可能性(见附录2)。我们不知道是谁最先注意到表达式
的值都将稳定在 2.71828 附近?详细的数学分析确实证实了这种有趣的可能性(见附录2)。我们不知道是谁最先注意到表达式  随着 n 趋于无穷大时的特殊行为,因此后来采用e 表示这个奇特数的确切日期仍不确定。然而,它的起源似乎可以追溯到17 世纪初,大约在 Napier 发明对数的同一时期。(正如我们所见,Edward Wright对 Napier的 “对数说明书(Descriptio)”[1618] 的译本第二版间接引用了e。) 这一时期的标志是国际贸易的巨大增长,各种金融交易激增;结果,人们对复利法则给予了极大的关注,并且数e 可能在这种情况下得到了第一个认可。然而,我们很快就会看到,与复利无关的问题也几乎在同一时间导出了这个相同的数。但在我们转向研究这些问题之前,我们最好仔细看看 e 的根(root)的数学过程:极限过程。
随着 n 趋于无穷大时的特殊行为,因此后来采用e 表示这个奇特数的确切日期仍不确定。然而,它的起源似乎可以追溯到17 世纪初,大约在 Napier 发明对数的同一时期。(正如我们所见,Edward Wright对 Napier的 “对数说明书(Descriptio)”[1618] 的译本第二版间接引用了e。) 这一时期的标志是国际贸易的巨大增长,各种金融交易激增;结果,人们对复利法则给予了极大的关注,并且数e 可能在这种情况下得到了第一个认可。然而,我们很快就会看到,与复利无关的问题也几乎在同一时间导出了这个相同的数。但在我们转向研究这些问题之前,我们最好仔细看看 e 的根(root)的数学过程:极限过程。
说明与资料来源:
1. 参见 HowardEves 所著<< AnIntroduction to the History of Mathematics>>(数学简史)(1964年初版; Philadelphia: SaundersCollege Publishing, 1983重印)第36页。
2. 参见 CarlB. Boyer 所著<<A History of Mathematics>>(数学史,修订版)( NewYork: John Wiley,1989出版)第36页。
3. 同2.,第35页。
4. 当然,差额还是和本金成正比的。如果我们投资1,000,000 美元而不是100 美元,那么如果按年复利计算,我们在第一年末的余额将为1,050,000 美元,而如果按日复利计算则为1,051,267.50 美元——相差1267.50 美元。你总是有钱更好!
内容来源:
<<e:The story of a number>> (数e的故事) 作者:Eli Maor
相关文章:

理解对数——金融问题中的自然对数(以e为底的对数)
第3章 金融问题(Financial Matters)——金融问题中的自然对数If thou lend moneyto any ofMy people. ...thou shalt not beto him as a creditor;neither shall yelay upon him interest.(如果你借钱给我的任何人。 ……你不应该是他的债权人;也不可向他加息。)——…...

vue2进阶学习之路
HTML、CSS和JavaScript基础 在学习Vue2之前,需要掌握HTML、CSS和JavaScript的基础知识。包括HTML的标签、CSS的布局和样式、JavaScript的变量类型、条件语句、循环语句等。 Vue2的基础知识 掌握Vue2的基本概念和语法,包括Vue2实例、数据绑定、指令、组件…...

决策树ID3算法
1. 决策树ID3算法的信息论基础 机器学习算法其实很古老,作为一个码农经常会不停的敲if, else if, else,其实就已经在用到决策树的思想了。只是你有没有想过,有这么多条件,用哪个条件特征先做if,哪个条件特征后做if比较优呢&#…...

C++模板基础(一)
函数模板(一) ● 使用 template 关键字引入模板: template void fun(T) {…} – 函数模板的声明与定义 – typename 关键字可以替换为 class ,含义相同 – 函数模板中包含了两对参数:函数形参 / 实参;模板形…...
)
生产者消费者模型线程池(纯代码)
目录 生产者消费者模型 条件变量&&互斥锁(阻塞队列) makefile Task.hpp BlockQueue.hpp BlockQueueTest.cc 信号量&&互斥锁(环形队列) makefile RingQueue.hpp RingQueueTest.cc 线程池(封…...

K8s 应用的网络可观测性: Cilium VS DeepFlow
随着分布式服务架构的流行,特别是微服务等设计理念在现代应用普及开来,应用中的服务变得越来越分散,因此服务之间的通信变得越来越依赖网络,很有必要来谈谈实现微服务可观测性中越来越重要的一环——云原生网络的可观测。K8s 是微服务设计理念能落地的最重要的承载体,本文…...
3.29面试题
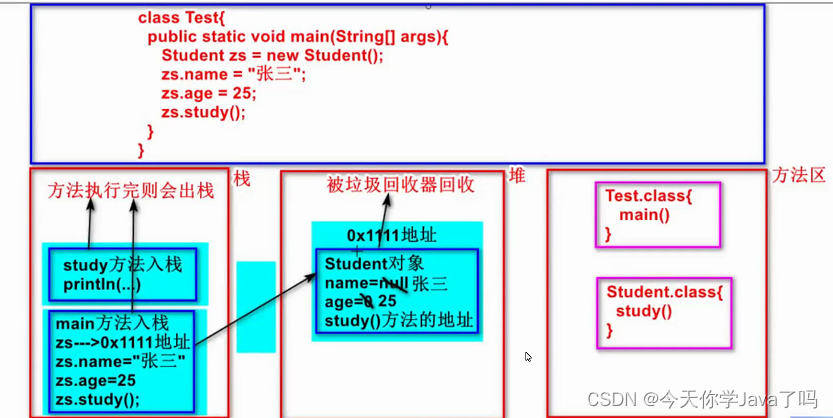
文章目录内存内存管理执行过程要点面试题内存 内存管理 由JVM管理 堆:new出来的对象(包括成员变量、数组元素、方法的地址)栈:局部变量(包括方法的参数)方法区:.class字节码文件(…...
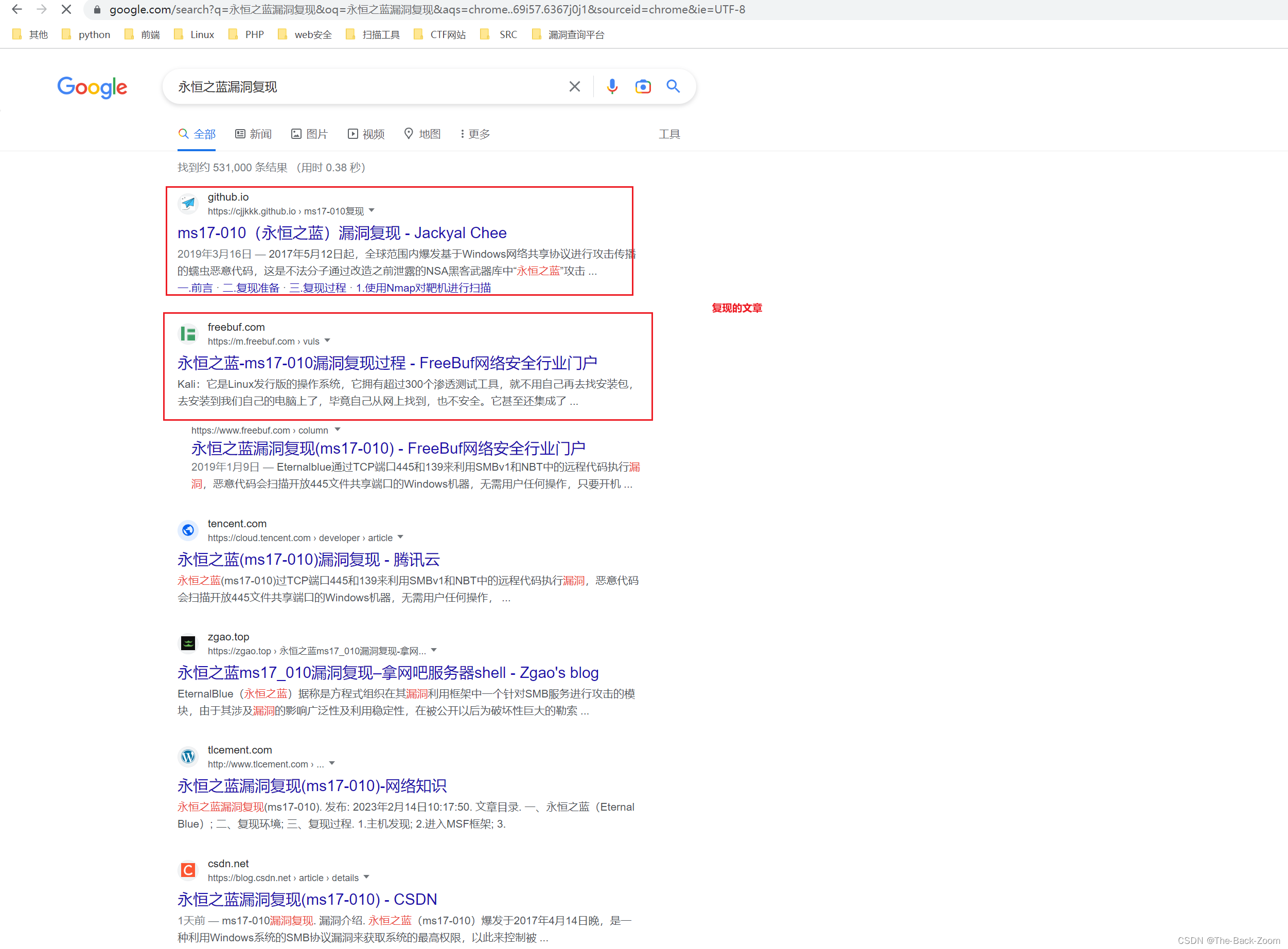
操作系统漏洞发现
操作系统漏洞发现前言一、操作系统漏洞发现1.1 namp2. Goby3. Nessus二,进行渗透测试2.1 使用工具进行渗透1. metasploit2.2 EXP2.3 复现文章三,操作系统漏洞修复前言 不管是对于App来说,还是web站点来说,操作系统是必须的&#x…...
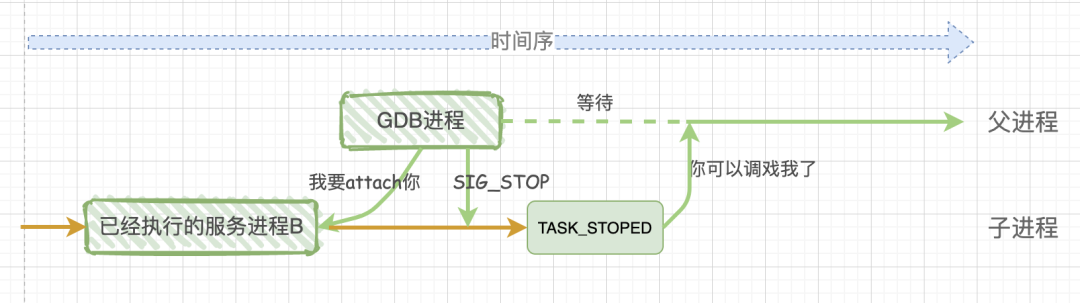
Linux gdb调试底层原理
TOC 前言 linux下gdb调试程序操作过程参考本人文章:gdb调试操作; 这里不再叙述; 本文主要内容是介绍GDB本地调试的底层调试原理,我们来看一下GDB是通过什么机制来控制被调试程序的执行顺序; 总结部分是断点调试的底层原理,可以直接跳转过去先看看大概…...
)
LC-1647. 字符频次唯一的最小删除次数(哈希+计数)
1647. 字符频次唯一的最小删除次数 难度中等56 如果字符串 s 中 不存在 两个不同字符 频次 相同的情况,就称 s 是 优质字符串 。 给你一个字符串 s,返回使 s 成为 优质字符串 需要删除的 最小 字符数。 字符串中字符的 频次 是该字符在字符串中的出现…...

HTTP状态码
100: 接受,正在继续处理 200: 请求成功,并返回数据 201: 请求已创建 202: 请求已接受 203: 请求成为,但未授权 204: 请求成功,没有内容 205: 请求成功,重置内容 206: 请求成功,返回部分内容 301: 永久性重定…...

【Linux】初见“which命令”,“find命令”以及linux执行命令优先级
文章目录1.which命令1.1 whereis命令1.2 locate命令1.3 搜索文件命令总结2.find命令2.1 find之exec用法2.2 管道符之xargs用法3 Linux常用命令4.命令执行优先级1.which命令 查找命令文件存放目录 搜索范围由环境变量PATH决定(echo $PATH) which命令格式࿱…...

update case when 多字段,多条件, mysql中case when用法
文章目录 前言 sql示例 普通写法: update case when写法 update case when 多字段写法 case when语法 case when 的坑 1、不符合case when条件但是字段被更新为null了 解决方法一:添加where条件 解决方法二:添加else 原样输出 2、同一条数据符…...
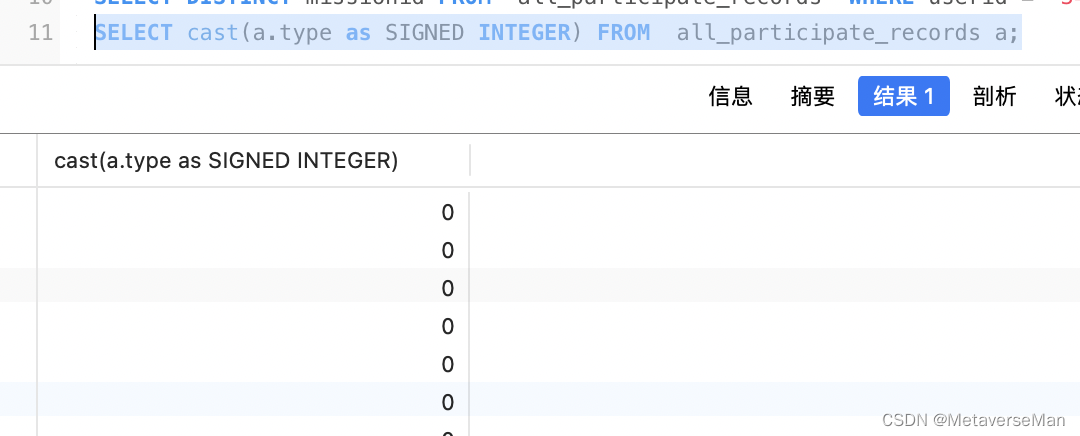
mysql隐式转换 “undefined“字符串匹配到mysql int类型0值字段
描述:mysql 用字符串搜索 能搜到int类型查询结果 mysql int类型条件用字符串查询 table: CREATE TABLE all_participate_records (id bigint unsigned NOT NULL AUTO_INCREMENT,created_at datetime(3) DEFAULT NULL,updated_at datetime(3) DEFAULT NULL,deleted…...

Redis八股文
1.Redis是什么? Redis 是一个基于 C 语言开发的开源数据库(BSD 许可),与传统数据库不同的是 Redis 的数据是存在内存中的(内存数据库),读写速度非常快,被广泛应用于缓存方向。并且,…...

InnoDB——详细解释锁的应用,一致性读,自增长与外键
一致性非锁定读 一致性的非锁定读(consistent nonlocking read)是指InnoDB存储引擎通过行多版本控制的方式读取当前执行时数据库中行的数据。 如果读取的行正在执行 行Delete或Update操作,这时读取操作不会因此去等待行上锁的释放。相反&…...

C++模板基础(四)
函数模板(四) ● 函数模板的实例化控制 – 显式实例化定义: template void fun(int) / template void fun(int) //header.h template<typename T> void fun(T x) {std::cout << x << std::endl; }//main.cpp #include&quo…...

pycharm使用记录
文章目录下载安装后续其他设置编辑器设置关于debug下载安装 直接去pycharm官网下载社区版,这个版本本来就是免费的,而且功能其实已经够了 后续其他设置 首先,第一次启动时,记得在preference->interpreter中设置python环境&a…...

Linux命令·kill·killall
Linux中的kill命令用来终止指定的进程(terminate a process)的运行,是Linux下进程管理的常用命令。通常,终止一个前台进程可以使用CtrlC键,但是,对于一个后台进程就须用kill命令来终止,我们就需…...

Linux /proc/version 文件解析
/proc/version文件里面的内容: Linux version 4.14.180-perf (oe-user@oe-host) (clang version 10.0.5 for Android NDK, GNU ld (GNU Binutils) 2.29.1.20180115) #1 SMP PREEMPT Wed Mar 29 18:55:02 CST 2023 /proc/version文件里面记录了如下内容: 1、Linux kernel的…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
