优化理论及应用精解【9】
文章目录
- 二次型函数
- 二次型函数详细解释
- 一、定义
- 二、性质
- 三、应用
- 四、示例
- 五、图表辅助说明(由于文本限制,无法直接提供图表)
- “西尔维斯特准则”
- 一、定义
- 二、来源
- 三、应用场景
- 参考文献
二次型函数
二次型函数详细解释
一、定义
二次型函数,也称为二次形式或二次型,是数学中一个重要的概念,特别是在线性代数和二次规划等领域。在实数域上,一个二次型可以表示为一个二次齐次多项式,即所有项的次数都是2,并且每一项的系数都是实数。在更一般的情况下,二次型是一个在向量空间上的函数,其输出是一个标量,并且满足特定的性质(如齐次性和对称性)。
具体来说,对于一个n维向量 x = ( x 1 , x 2 , . . . , x n ) T x = (x_1, x_2, ..., x_n)^T x=(x1,x2,...,xn)T,一个二次型可以表示为:
f ( x ) = ∑ i = 1 n ∑ j = 1 n a i j x i x j f(x) = \sum_{i=1}^{n} \sum_{j=1}^{n} a_{ij} x_i x_j f(x)=i=1∑nj=1∑naijxixj
其中, a i j a_{ij} aij是实数系数,并且通常假设矩阵 A = ( a i j ) A = (a_{ij}) A=(aij)是对称的(即 a i j = a j i a_{ij} = a_{ji} aij=aji)。
二、性质
- 齐次性:二次型函数是齐次的,意味着对于任何实数k和向量x,都有 f ( k x ) = k 2 f ( x ) f(kx) = k^2f(x) f(kx)=k2f(x)。
- 对称性:如果二次型的系数矩阵A是对称的,那么二次型本身也是对称的。这意味着对于任何两个向量x和y,都有 f ( x + y ) + f ( x − y ) = 2 [ f ( x ) + f ( y ) ] f(x+y) + f(x-y) = 2[f(x) + f(y)] f(x+y)+f(x−y)=2[f(x)+f(y)]。
- 正定性:一个二次型可以是正定的、负定的、半正定的、半负定的或不定的。这取决于其系数矩阵A的特征值。例如,如果A的所有特征值都是正的,那么二次型是正定的。
- 矩阵表示:二次型可以用矩阵形式简洁地表示。如果A是系数矩阵,x是向量,那么二次型可以写为 f ( x ) = x T A x f(x) = x^T A x f(x)=xTAx。
三、应用
- 最优化:在二次规划中,目标函数通常是一个二次型,约束条件是线性的。这类问题在经济学、工程学、物理学等领域有广泛应用。
- 线性代数:二次型在特征值问题、矩阵对角化等方面有重要作用。例如,通过求解二次型的特征值,可以了解矩阵的性质,如是否可逆、是否有重根等。
- 几何学:在几何学中,二次型可以用来描述二次曲面(如椭圆、双曲线、抛物面等)的方程。
四、示例
考虑一个二维向量 x = ( x 1 , x 2 ) T x = (x_1, x_2)^T x=(x1,x2)T,和一个二次型函数:
f ( x ) = 2 x 1 2 + 3 x 2 2 + 4 x 1 x 2 f(x) = 2x_1^2 + 3x_2^2 + 4x_1x_2 f(x)=2x12+3x22+4x1x2
这可以写成矩阵形式:
f ( x ) = x T A x f(x) = x^T A x f(x)=xTAx
其中,
A = ( 2 2 2 3 ) A = \begin{pmatrix} 2 & 2 \\ 2 & 3 \end{pmatrix} A=(2223)
为了更直观地理解这个二次型,我们可以考虑其图形表示。由于这是一个二维二次型,其图形是一个二次曲线(可能是椭圆、双曲线的一支或抛物线,具体取决于矩阵A的性质)。在这个例子中,由于矩阵A的所有特征值都是正的(可以通过计算验证),所以这是一个正定二次型,其图形是一个椭圆。
五、图表辅助说明(由于文本限制,无法直接提供图表)
- 二次曲线图形:可以绘制出二次型 f ( x ) = 2 x 1 2 + 3 x 2 2 + 4 x 1 x 2 f(x) = 2x_1^2 + 3x_2^2 + 4x_1x_2 f(x)=2x12+3x22+4x1x2的图形,显示为一个椭圆。这可以通过在平面上取一系列点 ( x 1 , x 2 ) (x_1, x_2) (x1,x2),计算每个点的函数值 f ( x ) f(x) f(x),并将这些点连接起来来实现。
- 系数矩阵特征值:可以计算出矩阵A的特征值,并说明这些特征值如何决定二次型的性质(如正定性)。
综上所述,二次型函数是一个在数学和实际应用中都非常重要的概念。通过理解其定义、性质和应用,我们可以更好地解决与之相关的问题,并在各个领域中发挥其作用。
“西尔维斯特准则”
是一个在数学领域中,特别是在线性代数部分,经常被提及的重要概念。下面将对其定义、来源、应用场景进行详细解释和说明。
一、定义
西尔维斯特准则(Sylvester’s Criterion),也被称为西尔维斯特定理的一个应用方面,是判断一个实对称矩阵是否为正定矩阵的一个有效方法。正定矩阵是一类特殊的矩阵,其所有特征值都是正数,且对于任意非零向量x,都有 x T A x > 0 x^TAx > 0 xTAx>0(其中A为正定矩阵)。西尔维斯特准则指出,一个实对称矩阵A为正定矩阵的充分必要条件是A的所有顺序主子式都是正数。顺序主子式是指矩阵A的前k行和前k列(k从1到n)所构成的k阶子矩阵的行列式。
二、来源
西尔维斯特准则是由英国数学家詹姆斯·约瑟夫·西尔维斯特(James Joseph Sylvester)提出并证明的。西尔维斯特是19世纪著名的数学家,他在代数、数论、矩阵论等多个领域都有杰出贡献。西尔维斯特准则作为矩阵论中的一个重要定理,被广泛应用于线性代数及相关领域的研究中。
三、应用场景
西尔维斯特准则在实际应用中有非常广泛的作用,特别是在需要判断矩阵正定性的场景中。以下是一些具体的应用场景:
-
优化问题:在求解二次规划、线性规划等优化问题时,目标函数或约束条件往往可以表示为二次型的形式。此时,如果目标函数的二次项系数矩阵是正定的,那么该问题就是一个凸优化问题,具有全局最优解。利用西尔维斯特准则可以快速判断矩阵的正定性,从而确定问题的凸性。
-
控制系统稳定性分析:在控制理论中,系统的稳定性分析是一个核心问题。对于线性时不变系统,其稳定性可以通过判断系统矩阵的特征值来实现。而系统矩阵的正定性或负定性,往往与系统的稳定性有密切关系。西尔维斯特准则可以用于判断系统矩阵的正定性或负定性,从而为系统的稳定性分析提供有力工具。
-
统计学和概率论:在统计学和概率论中,协方差矩阵是一个重要的概念。协方差矩阵的正定性是保证数据具有某些良好性质(如非奇异性、可逆性等)的关键。利用西尔维斯特准则可以方便地判断协方差矩阵的正定性,从而对数据的质量进行评估和预处理。
-
数值分析:在数值分析领域,特别是在求解大型稀疏矩阵的特征值问题时,矩阵的正定性是一个重要的考量因素。西尔维斯特准则可以用于判断矩阵的正定性,从而指导算法的设计和实现。
总之,西尔维斯特准则作为判断实对称矩阵正定性的一个重要工具,在数学、物理学、工程学、经济学等多个领域都有广泛的应用。掌握西尔维斯特准则不仅有助于深入理解线性代数的基本原理和方法论思想;还有助于解决实际问题中的许多复杂难题。
参考文献
- 文心一言
相关文章:

优化理论及应用精解【9】
文章目录 二次型函数二次型函数详细解释一、定义二、性质三、应用四、示例五、图表辅助说明(由于文本限制,无法直接提供图表) “西尔维斯特准则”一、定义二、来源三、应用场景 参考文献 二次型函数 二次型函数详细解释 一、定义 二次型函…...

nginx实现https安全访问的详细配置过程
文章目录 前言什么是 HTTP?什么是 HTTPS?HTTP 和 HTTPS 的区别为什么 HTTPS 被称为安全的?配置过程配置自签名证书 前言 首先我们来简单了解一下什么是http和https以及他们的区别所在. 什么是 HTTP? HTTP,全称为“超…...

1. TypeScript基本语法
TypeScript 学习总结 TypeScript 是一种 JavaScript 的超集,增加了静态类型检查和编译时错误检测,从而提高了代码的可维护性和可靠性。以下是 TypeScript 的基础知识总结,包括语法、运算符、数据类型、变量声明和作用域。 ## 基本语法TypeS…...

C# UDP与TCP点发【速发速断】模式
1、UDP 客户端 //由于收发都在本机,所以只用一个IP地址 IPAddress addr IPAddress.Parse("127.0.0.1"); var ptLocal new IPEndPoint(addr,9001);//本机节点,用于发送var ptDst new IPEndPoint(addr,9002);//目标节点…...

pikachu下
CSRF(跨站请求伪造) CSRF(get) url变成了这样了,我们就可以新开个页面直接拿url去修改密码 http://pikachu-master/vul/csrf/csrfget/csrf_get_login.php?username1&password2&submitLogin CSRF(post) 这里只是请求的方式不同,…...

Go语言开发im-websocket服务和vue3+ts开发类似微信pc即时通讯
前言 IM即时通讯聊天, 为软件开发者打造,不依赖第三方sdk,完全用Go语言开发即时通讯服务,支持H5、Electron、Wails 、Uniapp和各种小程序的IM即时通讯, 快速实现私聊、群聊、在线客服!让你快速搭建一个微信聊天系统,打…...

Redis如何实现分布式锁
目录 获取锁: 释放锁: Lua脚本: Redisson 分布式锁是,满足分布式系统或集群模式下多进程可见并且互斥的锁,因为我们熟知的java中的锁只是在单体架构下单个jvm中才会生效,如果部署了多个jvm则会导致新的…...

面向对象程序设计之继承(C++)
1.继承的定义 1.1继承的概念 继承(inheritance)机制是⾯向对象程序设计使代码可以复⽤的最重要的⼿段,它允许我们在保持原有类特性的基础上进⾏扩展,增加⽅法(成员函数)和属性(成员变量),这样产⽣新的类,称派⽣类。继承 呈现了⾯向…...

IAPP发布《2024年人工智能治理实践报告》
文章目录 前言一、黑箱问题►透明度、可理解性与可解释性二、法律和政策中的注意事项►欧盟的《通用数据保护条例》►欧盟的AI法案►NIST的AI风险管理框架►美国的第14110号行政命令►《生成式人工智能服务管理暂行办法》►新加坡的AI验证三、实施人工智能治理►模型卡与系统卡…...

了解MySQL 高可用架构:主从备份
为了防止数据库的突然挂机,我们需要对数据库进行高可用架构。主从备份是常见的场景,通常情况下都是“一主一从/(多从)”。正常情况下,都是主机进行工作,从机进行备份主机数据,如果主机某天突然意外宕机,从机…...

[OpenCV] 数字图像处理 C++ 学习——15像素重映射(cv::remap) 附完整代码
文章目录 前言1.像素重映射理论基础2.代码实现(1) remap()细节(2)水平翻转(2)垂直翻转(3)旋转 180 度(4)径向扭曲 3.完整代码 前言 像素重映射将图像中的每个像素映射到新位置,实现图像的扭曲、校正等操作。在 OpenCV 中,cv::remap() 函数就是用于实现这…...

Oreace每日运维操作
一.Oreace每日运维操作 目录 一.Oreace每日运维操作 1.1、确认所有的INSTANCE状态正常 1.2、检查文件系统的使用(剩余空间) 1.3 lwh暗码,,、检查日志文件和trace文件记录 1.4 lwh、检查数据库当日备份…...

【XR】AR HUD
1. AR HUD(head up display)原理 目标: 产业链上的各大Tier1及PGU企业都在积极开发这一技术,许多厂家已推出LCOS样机,比如说水晶光电、华阳集团、瀚思通、疆程已在北京车展或去年的上海车展上展出了LCOS方案的AR-HUD样…...

C/C++内存管理——内存泄漏/内存碎片
一、什么是内存泄漏 内存泄漏指的是在程序运行过程中,已经分配给程序使用的内存没有得到及时和正确的释放,导致这部分内存无法被程序再次使用或者被操作系统回收。内存泄漏通常发生在动态分配的内存上,如果这部分内存没有被正确释放,随着时间的推移,越来越多的内存将被占…...

使用 GaLore 预训练LLaMA-7B
项目代码: https://github.com/jiaweizzhao/galorehttps://github.com/jiaweizzhao/galore 参考博客: https://zhuanlan.zhihu.com/p/686686751 创建环境 基础环境配置如下: 操作系统: CentOS 7CPUs: 单个节点具有 1TB 内存的 Intel CP…...
)
gitlab无法push(pre-receive hook declined)
如果是个人的项目,托管在官网,可以参考这位大佬的, GitLab新建项目后push reject提交失败的解决办法_push rejected-CSDN博客 如果是公司的项目,去项目成员里看自己的身份,如果只是developer,是无法push到…...
物品识别——基于python语言
目录 1.物品识别 2.模型介绍 3.文件框架 4.代码示例 4.1 camera.py 4.2 interaction.py 4.3 object_detection.py 4.4 main.py 4.5 运行结果 5.总结 1.物品识别 该项目使用Python,OpenCV进行图像捕捉,进行物品识别。我们将使用YOLO(…...

【PostgreSQL】安装及使用(Navicat/Arcgis),连接(C#)
简介 PostgreSQL 是一个功能强大的开源对象关系数据库系统 下载地址 PostgreSQL: Downloads 由于我电脑上安装的是arcgispro3.1所以需要下载对应的postgresql版本 PostgreSQL 12 对应的 PostGIS 版本主要是 3.5.0 或更高版本。 安装 一般设置为postgresql 安装扩展插件 此…...
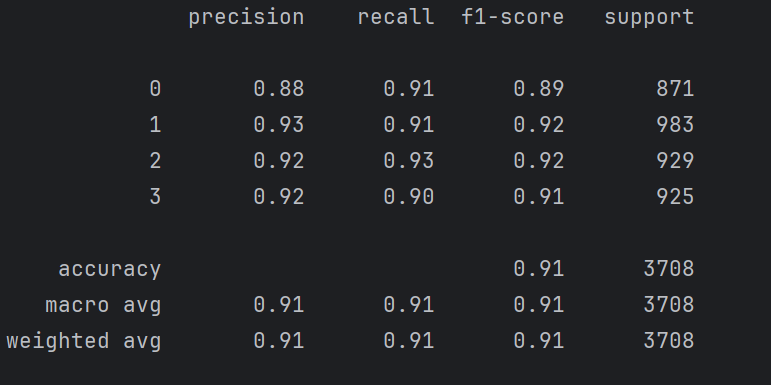
第L6周:机器学习-随机森林(RF)
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 目标: 1.什么是随机森林(RF) 随机森林(Random Forest, RF)是一种由 决策树 构成的 集成算法 &#…...

【电路笔记】-差分运算放大器
差分运算放大器 文章目录 差分运算放大器1、概述2、差分运算放大器表示2.1 差分模式2.2 减法器模式3、差分放大器示例3.1 相关电阻3.2 惠斯通桥3.3 光/温度检测4、仪表放大器5、总结1、概述 在之前的文章中,我们讨论了反相运算放大器和同相运算放大器,我们考虑了在运算放大器…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...
