双三次插值及MATLAB实现
一、双三次插值的概念
双三次插值(Bicubic interpolation),又叫双立方插值。在数值分析这个数学分支中,双三次插值是二维空间中最常用的插值方法。在这种方法中,函数f在点 (x0 ,y0) 的值不仅考虑其直接邻接点对其的影响,该方法通过矩形网格中最近的十六个采样点的加权平均得到,在这里需要使用两个多项式插值三次函数,每个方向使用一个。双三次插值是一种更加复杂的插值方式,它能创造出比双线性插值更平滑的图像边缘。双三次插值方法通常运用在一部分图像处理软件、打印机驱动程序和数码相机中,对原图像或原图像的某些区域进行放大。
补充知识:最邻近插值算法的目标像素值由源图上单个像素决定,双线性插值算法由源像素某点周围4个像素点按一定权重获得,而双立方插值算法更进一步参考了源像素某点周围4*4个像素来获得。
二、公式
双三次插值通过下式进行计算:
![]()
![]()
上式可简写为:

由上可知,对数字图像而言双三次插值算法是基于该像素最近4×4 邻域中的像素的加权平均值。
三、双三次插值的MATLAB实现
I = imread('ngc6543a.jpg');
imshow(I);
J = imresize(I,2,'bicubic');%使用双三次插值将图像放大到原始大小的 2倍。图像差值运算复杂,但图像质量好。
figure,imshow(J);
如果觉得本文对你和他人学习有所帮助,请关注、转发和点赞。谢谢大家!
相关文章:

双三次插值及MATLAB实现
一、双三次插值的概念 双三次插值(Bicubic interpolation),又叫双立方插值。在数值分析这个数学分支中,双三次插值是二维空间中最常用的插值方法。在这种方法中,函数f在点 (x0 ,y0) 的值不仅考虑其直接邻接点对其的影响…...
)
Kubernetes 持续集成与交付(CI/CD)
Kubernetes 持续集成与交付(CI/CD)详解 Kubernetes 是目前主流的容器编排平台,而在 DevOps 的实践中,持续集成与持续交付(CI/CD)是自动化软件开发与运维的核心环节。Kubernetes 与 CI/CD 的结合࿰…...

【Rust练习】14.流程控制
练习题来自:https://practice-zh.course.rs/flow-control.html 1 // 填空 fn main() {let n 5;if n < 0 {println!("{} is negative", n);} __ n > 0 {println!("{} is positive", n);} __ {println!("{} is zero", n);} } …...

React-Hooks-Form 集成 Zod 校验库
React-Hooks-Form 集成 Zod 校验库 首先需要安装 react hooks form 官方提交的解析器 npm install hookform/resolvers再安装校验库 npm install zod它不仅支持 Zod 校验库同时还支持目前各种主流的校验库比如:Yup、Zod、Joi、Ajv、Vest、Custom 具体查看官方文…...

kettle从入门到精通 第八十五课 ETL之kettle kettle中javascript步骤调用外部javascript/js文件
场景:交流学习群里面有小伙伴咨询kettle中的javascript代码步骤如何调用外部js文件中的函数,觉得有点意思的,于是就抽时间整理了一下。 1、外部js文件为test.js,代码如下: function test(param){return "接收到了…...
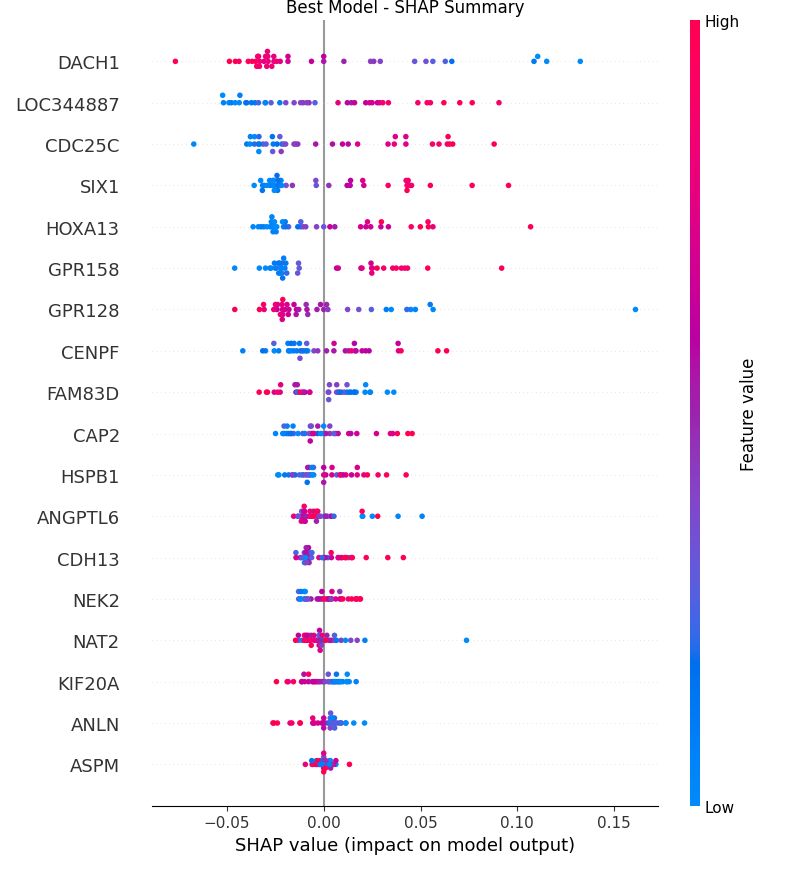
比传统机器学习更先进的深度学习神经网络的二分类建模全流程教程
比传统机器学习更先进的深度学习神经网络的二分类建模全流程分析教程 深度学习介绍和与传统机器学习的区别 深度学习(Deep Learning)是一种机器学习的分支,基于多层神经网络模型,能够自动从大量数据中学习特征并进行预测。深度学…...

TeamTalk梳理概括
文章目录 即时通讯重点概括展开聊聊单聊消息流转流程展开聊聊群聊消息流转流程群成员管理数据库MySQL连接池设计redis连接池设计文件传输原理实时性并发能力 db_proxy_server reactor响应处理流程单聊消息消息如何封装?如何保证对端完整解析一帧消息?协议…...

构建“零工市场小程序”,服务灵活就业“大民生”
如今,灵活就业已成为现代劳动力市场的重要组成部分。然而,这一就业形态也面临着信息不对称、匹配效率低下等一系列挑战。为有效解决这些问题,构建一个高效、便捷的“零工市场小程序”显得尤为重要。 二、零工市场现状与挑战 市场规模与增长趋…...

【组件】前端js HEIC/HEIF 转换为JPEG、PNG或GIF格式 苹果格式
【组件】前端js HEIC/HEIF 转换为JPEG、PNG或GIF格式 Heic2any: Client-side conversion of HEIC/HEIF image files to JPEG,PNG, or GIF in the browser.https://alexcorvi.github.io/heic2any/#demo GitHub - alexcorvi/heic2any: Converting HEIF/HEIF image formats to PN…...

Vue3中slot插槽的几种使用实践
【1】默认插槽 父组件 <Category title"今日美食城市"><img :src"imgUrl" alt""> </Category>子组件 <div class"category"><h2>{{title}}</h2><slot>默认内容</slot> </div&g…...

SSH工具 MobaXterm的使用与快捷配置
软件下载/安装与链接服务器/本地虚拟机 文章目录 软件下载/安装与链接服务器/本地虚拟机软件下载软件安装使用软件链接非本地机器并设置用户密码我不想有确定密码的弹窗 其余便捷配置配置右键粘贴SSH链接设置 软件下载 如果你访问不了这个网址,可以评论区找博主或者…...

git 远程分支同步本地落后的有冲突的分支
如果你的本地分支已经修改了很多代码,但同时也已经落后于远程分支。这个时候你需要在主分支上拉最新的代码,然后切换到你的分支。 如主分支是 main ,从分支是xing。 首先切换到子分支 $ git checkout xing 然后请求merge主分支main的代码 …...

如何基于Java解析国密数字证书
一、说明 随着信息安全的重要性日益凸显,数字证书在各种安全通信场景中扮演着至关重要的角色。国密算法,作为我国自主研发的加密算法标准,其应用也愈发广泛。然而,在Java环境中解析使用国密算法的数字证书时,我们可能…...

java实现系统文件管理
java实现系统文件管理 环境:jdk17springbootVueElementUI 背景:公司所做的项目需要别的系统向我们服务器上传文件,当我们需要查看这些文件什么时候上传的、文件数据是怎样的,只能去机房,排查问题效率较低,…...
pytorch快速入门(一)—— 基本工具及平台介绍
前言 该pytorch学习笔记应该配合b站小土堆的《pytorch深度学习快速入门教程》使用 环境配置:Anaconda Python编译器:pycharm、jupyter 两大法宝函数 dir():知道包中有什么东西(函数 / 属性..…...
『功能项目』怪物的有限状态机【42】
本章项目成果展示 我们打开上一篇41项目优化 - 框架加载资源的项目, 本章要做的事情是按照框架的思想构建项目并完成怪物的自动巡逻状态,当主角靠近怪物时,怪物会朝向主角释放技能 首先新建脚本:BossCtrl.cs (通常把xxxCtrl.cs脚…...

【C++】模板进阶:深入解析模板特化
C语法相关知识点可以通过点击以下链接进行学习一起加油!命名空间缺省参数与函数重载C相关特性类和对象-上篇类和对象-中篇类和对象-下篇日期类C/C内存管理模板初阶String使用String模拟实现Vector使用及其模拟实现List使用及其模拟实现容器适配器Stack与Queue 本章将…...

Python数据分析-世界上最富有的1000人
一、研究背景 随着全球化的加速发展和技术的进步,财富分配问题日益成为全球关注的焦点。财富的不平等现象日益明显,少数极富有的个人掌握了全球大部分的财富资源。了解全球最富有个人的财富分布及其背后的行业和国家因素,对于分析全球经济趋…...

CSS中隐藏滚动条的同时保留滚动功能
在CSS中,我们可以通过一些技巧来隐藏滚动条,同时保留滚动功能。以下是几种常用的方法和具体的实现步骤。 1. 使用 overflow 和 ::-webkit-scrollbar 这种方法适用于大多数现代浏览器。通过设置 overflow 属性启用滚动,同时利用 ::-webkit-s…...

我的标志:奇特的头像
<!DOCTYPE html> <html lang="zh-CN"> <head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=1.0"><title>与妖为邻</title><style>figu…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...
