牛客周赛 Round 60(A,B,C,D,E,F)
比赛链接
官方题解
这场基本都是数学题,官方题解讲的还不错,F能听懂的话其实不难。E是一个球盒模型的组合问题,F是化简递推式,成环时的解决方法很不错。
A 困难数学题
思路:
一个数异或两次结果为 0 0 0,异或四次结果也是 0 0 0
code:
#include <iostream>
#include <cstdio>
using namespace std;int main(){cout<<0<<endl;return 0;
}
B 构造序列
思路:
如果正负数个数差不多,正常排就可以。
但是如果有一种数数量很多,比如正数很多,我们只能正负相间来排,不过我们可以让首尾为正数,这样用到的正数就会尽可能多,假设一共有 2 n + 1 2n+1 2n+1 个数,那么正数就会用到 n + 1 n+1 n+1 个。
所以看一下多的那种数是否超过 少的数+1 个,多出来的部分就用不到了。
code:
pypy3 的代码,不过应该挺好理解的
x,y = [int(i) for i in input().split()]if x > y:t = xx = yy = tif y > x+1:print(2*x+1)
else:print(x+y)
C 连点成线
思路:
其实可以发现问题可以转化成对每一行找两头的点算距离,以及对每一列找两头的点算距离,因为中间的点一定不可能是最长的,所以不用看。而且对于列的计算,我们可以将行列坐标翻转,然后按行来做。
那么我们现在只需要对每一行找两头的点算距离,之后翻转行列坐标再算一次即可。这一步做法很多,先排序,可以枚举行坐标然后双指针找两端的点,也可以按横坐标升序来枚举点的横坐标,二分来找两端的纵坐标。
code:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define pii pair<int,int>
const int maxn=1e5+5;int n,m;
pii a[maxn];int calc(){//x相同 y的最大差值 sort(a+1,a+m+1);int ans=0;for(int l=1,r;l<=m;l=r+1){r=upper_bound(a+1,a+m+1,pii(a[l].first,n))-a-1;ans=max(ans,a[r].second-a[l].second);}return ans;
}int main(){cin>>n>>m;for(int i=1;i<=m;i++){auto &[x,y]=a[i];cin>>x>>y;}int ans=calc();for(int i=1;i<=m;i++){auto &[x,y]=a[i];swap(x,y);}ans=max(ans,calc());cout<<ans<<endl;return 0;
}
D 我们N个真是太厉害了
思路:
说白了就是给你 n n n 个数,问你用这些数无法表示的最小的数是多少。
我们可以对 n n n 个数排个序,假设用前 i − 1 i-1 i−1 个数最大可以表示到 m x mx mx(也就是说前 i − 1 i-1 i−1 个数可以表示 0 ∼ m x 0\sim mx 0∼mx 任何一个数),如果 a i ≤ m x + 1 a_i\le mx+1 ai≤mx+1,那么低于 m x mx mx 的数可以用前 i − 1 i-1 i−1 个数来凑,而高于 m x mx mx 的数可以通过使用 a i a_i ai 来凑,最多可以凑到 a i + m x a_i+mx ai+mx。
否则如果 a i > m x + 1 a_i> mx+1 ai>mx+1,那么就会出现至少 m x + 1 mx+1 mx+1 无法被表示的情况,因为我们已经排好序了,后续的 a j a_j aj 肯定都 > m x + 1 >mx+1 >mx+1,所以最小的无法表示的数就是 m x + 1 mx+1 mx+1。
我们维护 m x mx mx,如果能继续往下凑就加入 m x mx mx,否则我们就找到了第一个无法表示的数,也就是答案。
code:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn=1e5+5;int T,n;
int a[maxn];int calc(){int mx=0;for(int i=1;i<=n;i++){if(a[i]>mx+1)return mx+1;else {mx+=a[i];if(mx>=n)return -1;}}return -1;
}int main(){cin>>T;while(T--){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];sort(a+1,a+n+1);int ans=calc();if(~ans)cout<<ans<<endl;else cout<<"Cool!"<<endl;}return 0;
}
E 折返跑
思路:
因为两边的杆子要占两个格子,所以实际上能移动的距离是 n − 2 n-2 n−2。因为跑 m m m 趟,第一趟和最后一趟不移动杆子,所以实际上就只移动了 m − 1 m-1 m−1 次杆子。
我们每次至少移动一格杆子,不能把杆子移动的总长度超过两个杆子的总距离。而且我们还能把移动左右两边的杆子都看作是移动一根杆子,因为不管移动哪个杆子,两个杆子的相对距离变化是一样的。
这就有点像球盒模型了。我们把一格看成一个小球,把每一趟移动杆子的距离看成盒子,把球放入盒子看成让这一趟移动杆子的距离增加一格。那么这就是一个将 n − 2 n-2 n−2 个相同的小球放入 m − 1 m-1 m−1 个不同盒子,不能空盒,可以剩球的球盒模型。
球盒模型不可以剩球,但是我们可以多加入一个新的盒子,将 n − 2 n-2 n−2 个相同的小球放入 m m m 个不同盒子,放入新盒的球看作剩下的球就行了(也就是垃圾桶)。这样的话就转化成了经典的球盒模型,使用隔板法来做。
将 n − 2 n-2 n−2 个相同的小球放入 m m m 个不同盒子,不能空盒。既然不能空盒,就向每个盒子里预先加入一个小球, m − 1 m-1 m−1 个不能空盒的盒子各放入一个,球剩下 n − m − 1 n-m-1 n−m−1 个,这样就转化成了 将 n − m − 1 n-m-1 n−m−1 个相同的小球放入 m m m 个不同盒子,可以空盒 的问题了,向 n − m − 1 + ( m − 1 ) = n − 2 n-m-1+(m-1)=n-2 n−m−1+(m−1)=n−2 个位置上放入 m − 1 m-1 m−1 个隔板,其余位置放小球,这样分割出来的 m m m 个区间看作放入盒子的方法,方案数就是 C n − 2 m − 1 C_{n-2}^{m-1} Cn−2m−1 了。
code:
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=1e6+5;
const int N=1e6;
typedef long long ll;
const ll mod=1e9+7;ll qpow(ll a,ll b){ll base=a%mod,ans=1;b%=mod;while(b){if(b&1)ans=ans*base%mod;base=base*base%mod;b>>=1;}return ans;
}
ll inv(ll x){return qpow(x,mod-2);}int T,n,m;
ll fac[maxn],ifac[maxn];ll C(ll x,ll y){//C_x^yreturn fac[x]*ifac[y]%mod*ifac[x-y]%mod;
}int main(){cin>>T;fac[0]=1;for(int i=1;i<=N;i++)fac[i]=fac[i-1]*i%mod;ifac[N]=inv(fac[N]);for(int i=N;i>=1;i--)ifac[i-1]=ifac[i]*i%mod;while(T--){cin>>n>>m;cout<<C(n-2,m-1)<<endl;}return 0;
}
F 口吃
思路:
这个题在官方题解里讲的其实挺好的。
假设 f i f_i fi 表示讲第 i i i 个字的期望讲字的个数,根据题意可知 f n = 1 f_n=1 fn=1。根据题意不难列出: f 1 = 1 + a 1 a 1 + b 1 f 2 + b 1 a 1 + b 1 f 1 f_1=1+\dfrac{a_1}{a_1+b_1}f_2+\dfrac{b_1}{a_1+b_1}f_1 f1=1+a1+b1a1f2+a1+b1b1f1 f i = 1 + a i 2 ( a i + b i ) 2 f i + 1 + 2 a i b i ( a i + b i ) 2 f i + b i 2 ( a i + b i ) 2 f i − 1 f_i=1+\dfrac{a_i^2}{(a_i+b_i)^2}f_{i+1}+\dfrac{2a_ib_i}{(a_i+b_i)^2}f_{i}+\dfrac{b_i^2}{(a_i+b_i)^2}f_{i-1} fi=1+(ai+bi)2ai2fi+1+(ai+bi)22aibifi+(ai+bi)2bi2fi−1
整理可得: f 1 = f 2 + a 1 + b 1 a 1 f_1=f_2+\dfrac{a_1+b_1}{a_1} f1=f2+a1a1+b1 ( a i 2 + b i 2 ) f i = a i 2 f i + 1 + b i 2 f i − 1 + ( a i + b i ) 2 (a_i^2+b_i^2)f_i=a_i^2f_{i+1}+b_i^2f_{i-1}+(a_i+b_i)^2 (ai2+bi2)fi=ai2fi+1+bi2fi−1+(ai+bi)2
发现问题比较麻烦,因为这个递推式没法递推,如果我们从小到大递推的话,我们算 f i f_i fi 需要预先知道 f i + 1 f_{i+1} fi+1 的值,但是我们又没算出来,而算 f i + 1 f_{i+1} fi+1 的值又需要知道 f i f_i fi 的值,这时候就成环了(或者叫死锁)。
如果我们能把 f i + 1 f_{i+1} fi+1 或 f i − 1 f_{i-1} fi−1 的其中一个转化为 f i f_i fi,就可以打破这个死锁局面了。发现第一个 f 1 = f 2 + a 1 + b 1 a 1 f_1=f_2+\dfrac{a_1+b_1}{a_1} f1=f2+a1a1+b1 的式子可以带入到当 i = 2 i=2 i=2 时的 ( a 2 2 + b 2 2 ) f 2 = a 2 2 f 3 + b 2 2 f 1 + ( a 2 + b 2 ) 2 (a_2^2+b_2^2)f_2=a_2^2f_{3}+b_2^2f_{1}+(a_2+b_2)^2 (a22+b22)f2=a22f3+b22f1+(a2+b2)2 中,这样可以把 f 1 f_1 f1 转化为 f 2 f_2 f2,这时整个式子就变为了 f 2 f_2 f2 与 f 3 f_3 f3 的关系式,化简后会得到一个形为 f 2 = P ∗ f 3 + Q f_2=P*f_3+Q f2=P∗f3+Q 的形式。
而这个 f 2 f_2 f2 与 f 3 f_3 f3 的关系式可以类似地再次带入到 i = 3 i=3 i=3 时的式子 2 2 2 里,同理可以得到 f 3 f_3 f3 与 f 4 f_4 f4 的关系式,是一个形如 f 3 = P ∗ f 4 + Q f_3=P*f_4+Q f3=P∗f4+Q 的关系式,同理继续带入。
发现我们可以去递推算每一对 P , Q P,Q P,Q,然后从 n n n 往 1 1 1 递推 f 1 f_1 f1 即可。
假设 f i − 1 = P i − 1 ∗ f i + Q i − 1 f_{i-1}=P_{i-1}*f_{i}+Q_{i-1} fi−1=Pi−1∗fi+Qi−1,带入式子 2 2 2 得: ( a i 2 + b i 2 ) f i = a i 2 f i + 1 + b i 2 f i − 1 + ( a i + b i ) 2 (a_i^2+b_i^2)f_i=a_i^2f_{i+1}+b_i^2f_{i-1}+(a_i+b_i)^2 (ai2+bi2)fi=ai2fi+1+bi2fi−1+(ai+bi)2 ( a i 2 + b i 2 ) f i = a i 2 f i + 1 + b i 2 ( P i − 1 ∗ f i + Q i − 1 ) + ( a i + b i ) 2 (a_i^2+b_i^2)f_i=a_i^2f_{i+1}+b_i^2(P_{i-1}*f_{i}+Q_{i-1})+(a_i+b_i)^2 (ai2+bi2)fi=ai2fi+1+bi2(Pi−1∗fi+Qi−1)+(ai+bi)2 ( a i 2 + b i 2 ) f i = a i 2 f i + 1 + b i 2 P i − 1 ∗ f i + b i 2 Q i − 1 + ( a i + b i ) 2 (a_i^2+b_i^2)f_i=a_i^2f_{i+1}+b_i^2P_{i-1}*f_{i}+b_i^2Q_{i-1}+(a_i+b_i)^2 (ai2+bi2)fi=ai2fi+1+bi2Pi−1∗fi+bi2Qi−1+(ai+bi)2 ( a i 2 + b i 2 − b i 2 P i − 1 ) f i = a i 2 f i + 1 + b i 2 Q i − 1 + ( a i + b i ) 2 (a_i^2+b_i^2-b_i^2P_{i-1})f_i=a_i^2f_{i+1}+b_i^2Q_{i-1}+(a_i+b_i)^2 (ai2+bi2−bi2Pi−1)fi=ai2fi+1+bi2Qi−1+(ai+bi)2 f i = a i 2 a i 2 + b i 2 − b i 2 P i − 1 f i + 1 + b i 2 Q i − 1 + ( a i + b i ) 2 a i 2 + b i 2 − b i 2 P i − 1 f_i=\dfrac{a_i^2}{a_i^2+b_i^2-b_i^2P_{i-1}}f_{i+1}+\dfrac{b_i^2Q_{i-1}+(a_i+b_i)^2}{a_i^2+b_i^2-b_i^2P_{i-1}} fi=ai2+bi2−bi2Pi−1ai2fi+1+ai2+bi2−bi2Pi−1bi2Qi−1+(ai+bi)2因此: P i = a i 2 a i 2 + b i 2 − b i 2 P i − 1 , Q i = b i 2 Q i − 1 + ( a i + b i ) 2 a i 2 + b i 2 − b i 2 P i − 1 P_i=\dfrac{a_i^2}{a_i^2+b_i^2-b_i^2P_{i-1}},Q_i=\dfrac{b_i^2Q_{i-1}+(a_i+b_i)^2}{a_i^2+b_i^2-b_i^2P_{i-1}} Pi=ai2+bi2−bi2Pi−1ai2,Qi=ai2+bi2−bi2Pi−1bi2Qi−1+(ai+bi)2
code:
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
const ll mod=1e9+7;ll qpow(ll a,ll b){ll base=(a%mod+mod)%mod,ans=1;b%=mod;while(b){if(b&1)ans=ans*base%mod;base=base*base%mod;b>>=1;}return ans;
}
ll inv(ll x){return qpow(x,mod-2);}int n;
ll a[maxn],b[maxn];
ll p[maxn],q[maxn];
ll f[maxn];int main(){cin>>n;for(int i=1;i<n;i++)cin>>a[i];for(int i=1;i<n;i++)cin>>b[i];p[1]=1;q[1]=(a[1]+b[1])%mod*inv(a[1])%mod;for(int i=2;i<n;i++){ll A=a[i]*a[i]%mod,B=b[i]*b[i]%mod,C=(a[i]+b[i])*(a[i]+b[i])%mod;ll t=inv(((A+B-B*p[i-1])%mod+mod)%mod);p[i]=A*t%mod;q[i]=(B*q[i-1]+C)%mod*t%mod;}f[n]=1;for(int i=n-1;i>=1;i--){f[i]=p[i]*f[i+1]+q[i];f[i]%=mod;}cout<<f[1];return 0;
}
相关文章:
)
牛客周赛 Round 60(A,B,C,D,E,F)
比赛链接 官方题解 这场基本都是数学题,官方题解讲的还不错,F能听懂的话其实不难。E是一个球盒模型的组合问题,F是化简递推式,成环时的解决方法很不错。 A 困难数学题 思路: 一个数异或两次结果为 0 0 0ÿ…...
以及记录使用方法)
vueCropper裁剪图片(不模糊)以及记录使用方法
需求:上传限定比例的图片。前端框架是vue3 element plus。 问题:使用vueCropper后比例固定。但是上传后的图片很模糊 vueCropper官网 解决办法 vueCropper中有一个full和high两个参数,记得开启 const options: any reactive({img: , // 原…...
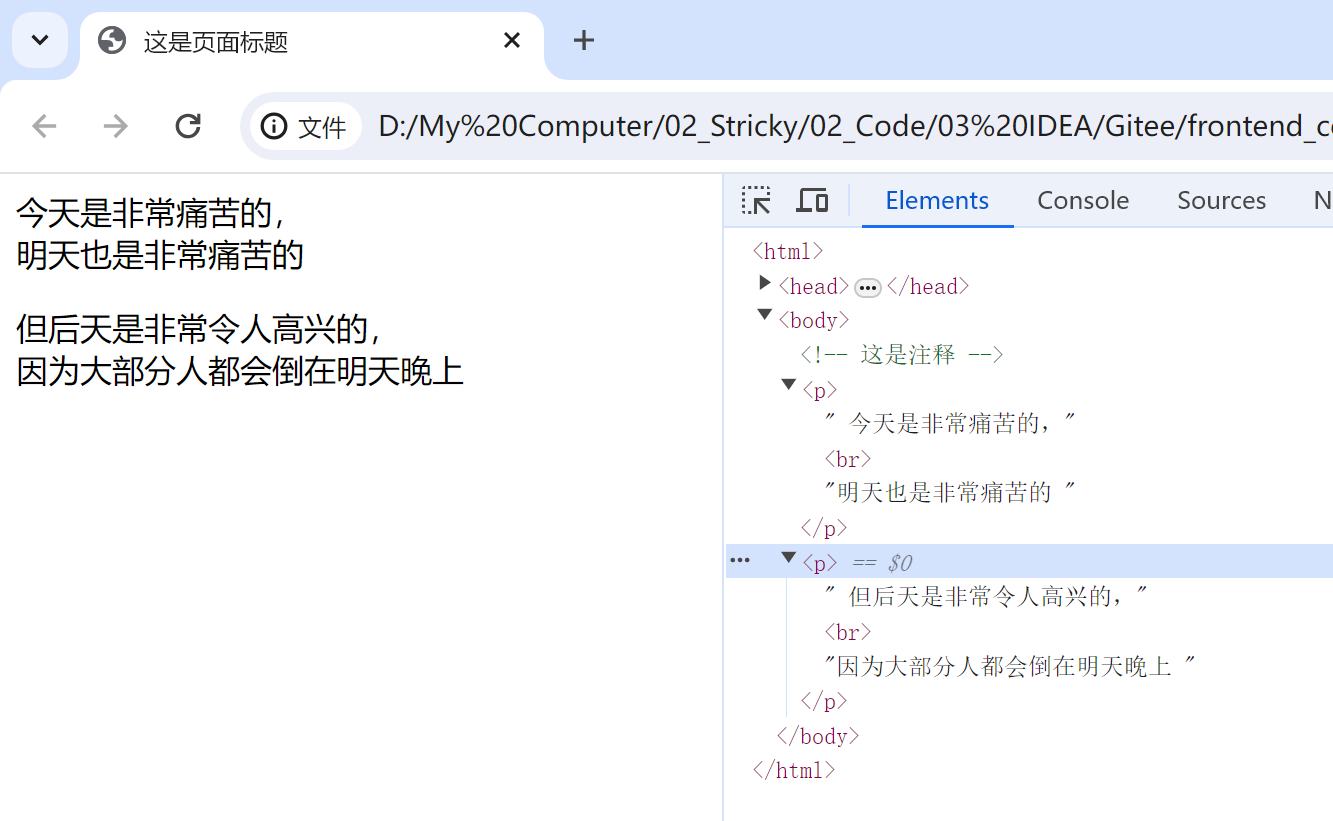
【HTML】HTML页面和常见标签
文章目录 什么是前端HTML 页面编写如何快速生成代码框架常见标签注释标签标题标签段落标签换行标签格式化标签 什么是前端 Web 前端,用来直接给以用户呈现的一个一个的网页。一个软件通常是由 后端前端 完成的 后端:通过 Java/C等语言,完成相…...

鸿蒙 ArkUI组件二
ArkUI组件(续) 文本组件 在HarmonyOS中,Text/Span组件是文本控件中的一个关键部分。Text控件可以用来显示文本内容,而Span只能作为Text组件的子组件显示文本内容。 Text/Span组件的用法非常简单和直观。我们可以通过Text组件来显…...

PHP 实现 redis 分布式锁
分布式锁 如果是强一致性保证,在获取锁或者失败后引入数据库存储扫表、mq 等方式进行补偿 如果可以容忍少量异常就不需要考虑了 像这里的代码,没吃建立一个链接铺货,性能损耗时间延迟也是很大的,也可在一块代码中进行服务&…...

vue3 自定义el-tree树形结构样式
这里样式设置主要用到了 windcss 实现效果 模拟数据 这里也可以用模拟的数据,下面用的是后端请求的真实数据 [{"id": 5,"rule_id": 0,"status": 1,"create_time": "2019-08-11 13:36:09","update_time": "…...
【网络安全】分享4个高危业务逻辑漏洞
未经许可,不得转载。 文章目录 正文逻辑漏洞1逻辑漏洞2逻辑漏洞3逻辑漏洞4其它正文 该目标程序是一家提供浏览器服务的公司,其核心功能是网页抓取和多账户登录操作,类似于浏览器中的隐身模式,但更加强大和高效。通过该平台,用户可以轻松管理并同时运行数百个隐身浏览器实…...

【装机教程】Visual Studio Community 2019离线安装
Visual Studio 2019离线安装 由于现在 官网只支持在线安装最新版的Visual Studio 2022,因此 Visual Studio Community 2019需要离线安装。 下载离线安装镜像,并解压。点击vs_setup.exe运行。 选择安装位置,四处位置需要确定。 选择语言包&…...

NumPy 线性代数
NumPy 线性代数 NumPy 是 Python 中用于科学计算的核心库之一,它提供了一个强大的数学函数库,特别是在处理大型多维数组和矩阵时表现出色。线性代数是 NumPy 的一个重要组成部分,它包含了大量的函数和运算符,用于执行矩阵和向量的…...

家装材料之水泥,最容易被忽视的基础材料!
由于水泥在装修中扮演辅料的角色,很多业主往往会忽视它们的质量。事实上,装修无小事,不能抱有抓大放小的态度。 更何况水泥是装修工程的基础材料,在家居装修中,地面、墙面的找平以及瓷砖、大理石的铺贴&#…...

openstack之keystone介绍
功能 keystone在OpenStack中负责: 管理:用户、租户和权限; 认证:组件相互访问的身份认证; 鉴权:提供 RBAC(Role Based Access Control) 权限体系; 服务注册与发现&#…...

【图像拼接】基于SIFT/SURF特征算法的图像拼接,matlab实现
博主简介:matlab图像代码项目合作(扣扣:3249726188) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 本次案例是基于SIFT/SURF特征算法的图像拼接,用matlab实现。 一、案例背景和算法介…...
《微信小程序实战(2) · 组件封装》
📢 大家好,我是 【战神刘玉栋】,有10多年的研发经验,致力于前后端技术栈的知识沉淀和传播。 💗 🌻 CSDN入驻不久,希望大家多多支持,后续会继续提升文章质量,绝不滥竽充数…...

LaTex2024 下载安装运行HelloWorld—全流程笔记
LaTex安装教程🚀 这是读博之后写的第一篇文章,来到新课题组之后,新课题组主要是用Latex,在之前的课题组,还是比较常用world,所以就研究了一下Latex的下载和安装,虽然网上已经有了不少教程&#…...

Golang | Leetcode Golang题解之第404题左叶子之和
题目: 题解: func isLeafNode(node *TreeNode) bool {return node.Left nil && node.Right nil }func sumOfLeftLeaves(root *TreeNode) (ans int) {if root nil {return}q : []*TreeNode{root}for len(q) > 0 {node : q[0]q q[1:]if no…...
基于yolov8+lprnet的中文车牌识别系统python源码+pytorch模型+精美GUI界面
【算法介绍】 基于YOLOv8和LPRNet的中文车牌识别系统是一种高效且准确的解决方案,结合了目标检测与字符识别的先进技术。YOLOv8作为最新的实时目标检测算法,以其高速度和精确度著称,能够迅速在图像或视频中定位车牌位置。LPRNet则是一种专为…...

电信创维光猫DT741超级密码
正常的D740系是创维系列光猫如:SK-D740 之类的超密获取办法-光猫/adsl/cable无线一体机-恩山无线论坛 但是我这个固件是DT741v1.0 我只能说很S -B,这个版本如果是1.02那就可以很轻松的去用通用办法解决,但是呢!还有办法就是用最传…...

PostgreSQL的流复制断点续传
PostgreSQL的流复制断点续传 PostgreSQL的流复制(Streaming Replication)具有断点续传的能力,这意味着当主节点和备用节点之间的连接由于网络故障等原因中断后,备用节点会自动从中断点继续接收WAL(Write-Ahead Loggin…...

【bug】通过lora方式微调sdxl inpainting踩坑
报错内容 ValueError: Attempting to unscale FP16 gradients. 报错位置 if accelerator.sync_gradients:params_to_clip (itertools.chain(unet_lora_parameters, text_lora_parameters_one, text_lora_parameters_two)if args.train_text_encoderelse unet_lora_parameters…...

[Python可视化]数据可视化在医疗领域应用:提高诊断准确性和治疗效果
随着医疗数据的增长,如何从庞大的数据集中快速提取出有用的信息,成为了医疗研究和实践中的一大挑战。数据可视化在这一过程中扮演了至关重要的角色,它能够通过图形的方式直观展现复杂的数据关系,从而帮助医生和研究人员做出更好的…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
