GAMES101（10~11节，几何）

Geometry

implicit隐式几何表示：

函数f(x,y,z)：

根据函数fn描述几何，遍历所有空间内 的点，如果带入xyz到函数f(x,y,z)结果=0那就绘制这个点

如果xyz求值结果>0表示在几何外，=0在表面,<0在几何内

构造几何csg( constructive solid geometry)：

建立bool运算（这被应用到建模软件中）

并集交集 \ 差集：通过建立基本几何形体，利用bool创建复杂几何

距离函数：

距离函数：任何点到几何表面的最近距离，

如果点在外面，函数结果为正，如果在内部，距离为负

比如当两个球逐渐靠近，会发生融合，这是对距离函数sdf做混合，用于渲染平滑的几何形状

比如：水滴融合

explicit显示几何表示：

直接表示（不会改变）：

point clouds点云：

几何由密集的点表示

Polygon / triangle meshes

由多边形网格表示：obj文件存储所有顶点数据的信息，和索引顺序

参数表示（输入参数，得到转换后的结果）：

参数映射方式：

遍历所有的UV坐标通过映射函数f(u,v) ，投影到空间中的某一点

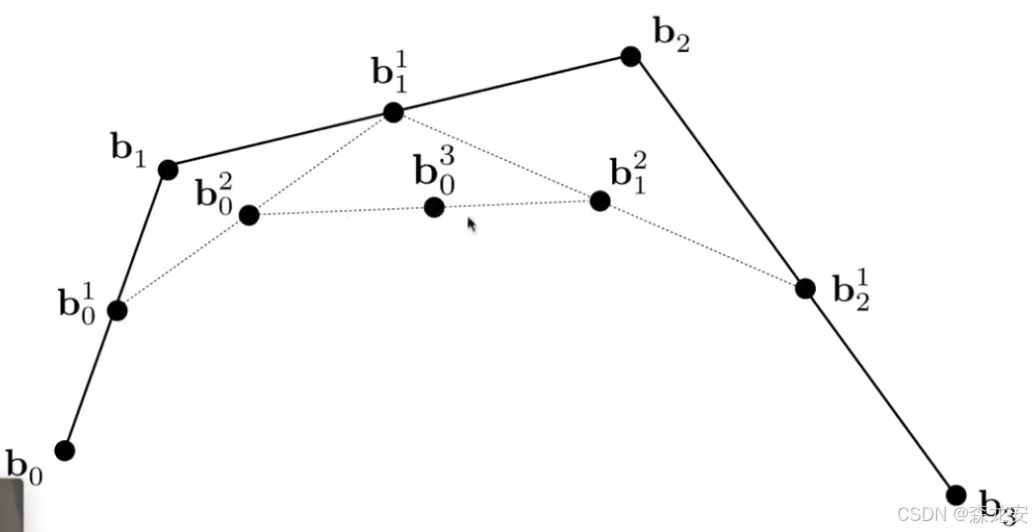
bezier surfaces贝塞尔曲线

用一系列控制点定义曲线，每个点相连形成连线

从所有连线取相同时间t（参数），再次相连，直到仅剩一个点为止，这个点作为曲线上的某一个点

重复上述，直到从每个线段取完所有可能t

标题

数学表达式：

bn(t)为贝塞尔曲线，j为控制点，时间t范围0--1，n是控制点总数

B(t)伯恩斯坦多项式

(n  i​) 是二项式系数，也称为组合数，表示从 n 个不同元素中取出 i 个元素的组合方式的数目

细分曲面

NURBS样条曲线

作业四

题目：

绘制Bézier 曲线，其中bezier函数负责绘制 Bézier 曲线，提供控制点序列，每次使t增加微小值，并调用recursive_bezier函数，负责返回 Bézier 曲线上对应点的坐标