MATLAB 在数学建模中的深入应用:从基础到高级实践
目录
前言
一、MATLAB基础知识
1.1 MATLAB工作环境简介
1.1.1 命令窗口(Command Window)
1.1.2 工作区(Workspace)
1.1.3 命令历史(Command History)
1.1.4 编辑器(Editor)
1.1.5 当前文件夹(Current Folder)
1.2 数据类型和基本操作
1.2.1 常用数据类型
1.2.2 矩阵和数组操作
创建矩阵和数组
基本矩阵运算
示例:矩阵运算
索引与切片
使用内置函数生成特殊矩阵
1.3 函数的定义与使用
1.3.1 定义函数
1.3.2 示例:计算两个数的最大公约数
1.4 常用内置函数
1.4.1 数学函数
1.4.2 统计函数
1.4.3 线性代数函数
二、数学建模的方法论
2.1 问题描述与分析
2.2 建立模型假设
2.3 建立数学模型
2.4 模型求解与验证
2.5 模型分析与改进
三、MATLAB在数学建模中的应用实例
3.1 实例一:人口增长模型
3.1.1 问题描述
3.1.2 建立模型
3.1.3 MATLAB求解
3.1.4 结果分析
3.2 实例二:SIR传染病模型
3.2.1 问题描述
3.2.2 建立模型
3.2.3 MATLAB求解
3.2.4 结果分析
3.3 实例三:谐振子运动模拟
3.3.1 问题描述
3.3.2 建立模型
3.3.3 MATLAB求解
3.3.4 结果分析
结论
参考文献与学习资源
前言
在科技迅猛发展的时代,数学建模已成为理解和解决复杂现实问题的关键工具。MATLAB作为一款功能强大的科学计算软件,凭借其高效的数值计算能力、丰富的函数库和直观的可视化功能,广泛应用于数学建模领域。本文将从以下三个部分深入探讨MATLAB在数学建模中的应用:
- MATLAB基础知识
- 数学建模的方法论
- MATLAB在数学建模中的应用实例
一、MATLAB基础知识
1.1 MATLAB工作环境简介
熟悉MATLAB的工作环境是高效进行数学建模的第一步。MATLAB的界面主要由以下部分组成:
1.1.1 命令窗口(Command Window)
- 功能:用于直接输入和执行命令,与MATLAB进行交互。
- 特点:即时反馈,适合测试简单的代码段。
1.1.2 工作区(Workspace)
- 功能:显示当前定义的变量及其数值,方便查看和管理数据。
- 特点:可直观地观察变量的变化。
1.1.3 命令历史(Command History)
- 功能:记录用户输入的所有命令,便于回溯和重复执行。
- 特点:支持命令搜索和再次执行。
1.1.4 编辑器(Editor)
- 功能:用于编写、编辑和调试脚本文件(.m文件)和函数文件。
- 特点:支持语法高亮、自动缩进和调试工具。
1.1.5 当前文件夹(Current Folder)
- 功能:显示当前工作目录下的文件和文件夹,便于管理项目文件。
- 特点:支持文件的创建、删除和重命名。
1.2 数据类型和基本操作
1.2.1 常用数据类型
| 数据类型 | 描述 | 示例 |
|---|---|---|
| 数值类型 | 整数、浮点数、复数 | a = 5; b = 3.14; |
| 字符类型 | 单个字符或字符数组 | c = 'hello'; |
| 字符串 | 字符串数组(从R2016b开始支持) | str = "world"; |
| 逻辑类型 | 真或假,true或false | flag = true; |
| 结构体 | 包含不同类型数据的集合 | s.name = 'John'; |
| 元胞数组 | 存储不同类型或大小的数据 | C = {1, 'text', [1,2]}; |
1.2.2 矩阵和数组操作
创建矩阵和数组
% 创建2x3矩阵
A = [1, 2, 3; 4, 5, 6];% 创建行向量
rowVec = [1, 2, 3, 4, 5];% 创建列向量
colVec = [1; 2; 3; 4; 5];
基本矩阵运算
| 运算符 | 描述 | 示例 |
|---|---|---|
+ | 矩阵加法 | C = A + B; |
- | 矩阵减法 | C = A - B; |
* | 矩阵乘法 | C = A * B; |
.* | 数组元素乘法 | C = A .* B; |
/ | 矩阵右除 | C = A / B; |
.\ | 数组元素右除 | C = A ./ B; |
^ | 矩阵乘方 | C = A ^ 2; |
.^ | 数组元素乘方 | C = A .^ 2; |
' | 矩阵转置 | A_T = A'; |
示例:矩阵运算
% 矩阵乘法(需满足矩阵乘法的维度要求)
A = [1, 2; 3, 4];
B = [5; 6];
C = A * B; % 结果为 [17; 39]% 数组元素乘法
D = A .* A; % 结果为 [1, 4; 9, 16]
索引与切片
% 访问矩阵元素
element = A(2, 1); % 结果为3% 提取矩阵的第一列
firstCol = A(:, 1); % 结果为 [1; 3]% 提取矩阵的子矩阵
subMatrix = A(1:2, 1:2); % 结果为 A 本身
使用内置函数生成特殊矩阵
| 函数 | 描述 | 示例 |
|---|---|---|
zeros(n,m) | 创建全零矩阵 | Z = zeros(2,3); |
ones(n,m) | 创建全一矩阵 | O = ones(3); |
eye(n) | 创建单位矩阵 | I = eye(4); |
rand(n,m) | 创建随机矩阵(均匀分布) | R = rand(2,2); |
randn(n,m) | 创建随机矩阵(正态分布) | N = randn(3,3); |
1.3 函数的定义与使用
1.3.1 定义函数
- 函数文件必须与函数名同名,扩展名为
.m。 - 函数的基本结构:
function [output1, output2, ...] = functionName(input1, input2, ...)% 函数说明% 输入参数:% input1 - 描述% input2 - 描述% 输出参数:% output1 - 描述% output2 - 描述% 函数体...
end
1.3.2 示例:计算两个数的最大公约数
function gcdValue = computeGCD(a, b)% 计算两个整数的最大公约数while b ~= 0temp = b;b = mod(a, b);a = temp;endgcdValue = a;
end
调用函数:
result = computeGCD(48, 18); % 结果为6
1.4 常用内置函数
1.4.1 数学函数
| 函数 | 描述 | 示例 |
|---|---|---|
abs(x) | 绝对值 | y = abs(-5); |
sqrt(x) | 平方根 | y = sqrt(16); |
exp(x) | 指数函数 | y = exp(1); |
log(x) | 自然对数 | y = log(2.71828); |
log10(x) | 常用对数 | y = log10(100); |
sin(x) | 正弦函数(弧度) | y = sin(pi/2); |
cos(x) | 余弦函数(弧度) | y = cos(0); |
tan(x) | 正切函数(弧度) | y = tan(pi/4); |
1.4.2 统计函数
| 函数 | 描述 | 示例 |
|---|---|---|
mean(x) | 平均值 | avg = mean([1, 2, 3, 4]); |
median(x) | 中位数 | med = median([1, 2, 3, 4]); |
mode(x) | 众数 | m = mode([1, 2, 2, 3, 4]); |
std(x) | 标准差 | s = std([1, 2, 3, 4]); |
var(x) | 方差 | v = var([1, 2, 3, 4]); |
sum(x) | 求和 | total = sum([1, 2, 3, 4]); |
prod(x) | 连乘积 | p = prod([1, 2, 3, 4]); |
max(x) | 最大值 | maxVal = max([1, 2, 3, 4]); |
min(x) | 最小值 | minVal = min([1, 2, 3, 4]); |
1.4.3 线性代数函数
| 函数 | 描述 | 示例 |
|---|---|---|
det(A) | 计算矩阵的行列式 | d = det([1, 2; 3, 4]); |
inv(A) | 计算矩阵的逆 | A_inv = inv([1, 2; 3, 4]); |
rank(A) | 矩阵的秩 | r = rank([1, 2; 3, 4]); |
eig(A) | 矩阵的特征值和特征向量 | [V, D] = eig([1, 2; 3, 4]); |
svd(A) | 奇异值分解 | [U, S, V] = svd(A); |
二、数学建模的方法论
2.1 问题描述与分析
- 明确问题:清晰地定义需要解决的实际问题。
- 背景调研:收集相关的背景信息和数据,理解问题的本质。
- 确定目标:设定模型需要达到的目标和要求。
2.2 建立模型假设
- 简化复杂性:对实际问题进行合理的简化,忽略次要因素。
- 设定条件:明确模型适用的范围、边界条件和初始条件。
- 变量选取:确定模型中的关键变量和参数。
2.3 建立数学模型
- 选择数学工具:根据问题性质,选择合适的数学方法(如微分方程、代数方程、统计模型等)。
- 建立关系式:根据物理定律、经验公式或统计关系,建立变量之间的数学关系。
- 模型表达:将问题形式化,得到可计算的数学模型。
2.4 模型求解与验证
- 求解模型:使用解析方法或数值方法求解模型。
- 算法选择:选择合适的算法和计算工具,确保计算的准确性和效率。
- 结果验证:将模型结果与实际数据或已知结果进行比较,验证模型的合理性。
2.5 模型分析与改进
- 结果分析:解释模型结果的物理意义或现实意义。
- 敏感性分析:研究模型对参数变化的敏感程度,识别关键参数。
- 模型改进:根据分析结果,调整模型结构或参数,提高模型的准确性和适用性。
三、MATLAB在数学建模中的应用实例
3.1 实例一:人口增长模型
3.1.1 问题描述
预测一个地区的人口增长情况,考虑出生率、死亡率和环境承载力等因素。
3.1.2 建立模型
采用Logistic增长模型,其微分方程为:
- P(t):人口数量
- r:固有增长率
- K:环境承载力
3.1.3 MATLAB求解
代码示例:
% 参数定义
r = 0.02; % 固有增长率
K = 1e7; % 环境承载力
P0 = 1e6; % 初始人口
tspan = [0, 100];% 时间范围(年)% 定义微分方程
dPdt = @(t, P) r * P * (1 - P / K);% 使用ode45求解
[t, P] = ode45(dPdt, tspan, P0);% 绘制结果
figure;
plot(t, P, 'LineWidth', 2);
xlabel('时间(年)');
ylabel('人口数量');
title('人口增长的Logistic模型');
grid on;
知识点讲解:
- Logistic模型:描述了有限资源条件下的人口增长,体现了人口数量的自我限制作用。
- ode45函数:MATLAB中用于求解常微分方程的数值方法,基于Runge-Kutta算法,适用于非刚性问题。
- 匿名函数:使用
@(t, P)定义微分方程,方便传递给ode45求解器。
3.1.4 结果分析
从图形上可以看到,人口增长在初期呈指数增长,当接近环境承载力时,增长速度减缓,最终趋于稳定。
3.2 实例二:SIR传染病模型
3.2.1 问题描述
模拟传染病在群体中的传播过程,分析易感者、感染者和康复者的人数变化。
3.2.2 建立模型
SIR模型的微分方程为:
- S(t):易感者人数
- I(t):感染者人数
- R(t):康复者人数
- N=S+I+RN :总人口
- β:传染率
- γ:康复率
3.2.3 MATLAB求解
代码示例:
% 参数定义
N = 1e5; % 总人口
beta = 0.3; % 传染率
gamma = 0.1; % 康复率
I0 = 1; % 初始感染者
S0 = N - I0; % 初始易感者
R0 = 0; % 初始康复者
tspan = [0, 160]; % 时间范围(天)% 微分方程定义
function dYdt = sirModel(t, Y)S = Y(1);I = Y(2);R = Y(3);dSdt = -beta * S * I / N;dIdt = beta * S * I / N - gamma * I;dRdt = gamma * I;dYdt = [dSdt; dIdt; dRdt];
end% 初始条件
Y0 = [S0; I0; R0];% 求解微分方程
[t, Y] = ode45(@sirModel, tspan, Y0);% 绘制结果
figure;
plot(t, Y(:,1), 'b', t, Y(:,2), 'r', t, Y(:,3), 'g', 'LineWidth', 2);
xlabel('时间(天)');
ylabel('人数');
legend('易感者', '感染者', '康复者');
title('SIR传染病模型模拟');
grid on;
知识点讲解:
- SIR模型:经典的传染病模型,反映了群体中个体在不同状态之间的转移。
- 函数句柄:
@sirModel表示将函数sirModel的句柄传递给ode45。 - 向量化:微分方程的状态变量以向量形式表示,便于处理多变量系统。
3.2.4 结果分析
- 感染者人数:先上升后下降,形成峰值。
- 易感者人数:持续下降。
- 康复者人数:持续上升,最终趋于稳定。
3.3 实例三:谐振子运动模拟
3.3.1 问题描述
模拟受迫阻尼谐振子的运动,分析其在外力作用下的动态行为。
3.3.2 建立模型
运动方程:
- m:质量
- c:阻尼系数
- k:弹性系数
- F(t):外力(如正弦驱动力)
将二阶微分方程转化为一阶微分方程组:
令 ,则:
3.3.3 MATLAB求解
代码示例:
% 参数定义
m = 1; % 质量,kg
c = 0.5; % 阻尼系数,N·s/m
k = 20; % 弹性系数,N/m
F0 = 5; % 驱动力幅值,N
omega = 2; % 驱动力角频率,rad/s
tspan = [0, 20]; % 时间范围,s
initialConditions = [0; 0]; % 初始位移和速度% 运动方程定义
function dxdt = oscillator(t, x)F = F0 * sin(omega * t);dxdt = [x(2); (F - c * x(2) - k * x(1)) / m];
end% 求解微分方程
[t, X] = ode45(@oscillator, tspan, initialConditions);% 绘制位移-时间曲线
figure;
plot(t, X(:,1), 'LineWidth', 2);
xlabel('时间(s)');
ylabel('位移(m)');
title('受迫阻尼谐振子运动模拟');
grid on;% 绘制相位图(位移-速度)
figure;
plot(X(:,1), X(:,2), 'LineWidth', 2);
xlabel('位移(m)');
ylabel('速度(m/s)');
title('相位图');
grid on;
知识点讲解:
- 二阶微分方程降阶:将高阶微分方程转换为一阶微分方程组,便于数值求解。
- 外力的表示:在模型中加入时间依赖的外力,模拟实际驱动力的作用。
- 相位图:通过绘制位移和速度的关系,分析系统的动力学特性。
3.3.4 结果分析
- 稳态振动:经过初始的过渡过程,系统进入稳态振动。
- 阻尼效应:阻尼使得振幅逐渐稳定,不会无限增大。
- 共振现象:若驱动力频率接近系统的固有频率,振幅会显著增加(可通过调整参数观察)。
结论
本文从MATLAB基础知识入手,详细介绍了数学建模的方法论,并通过三个具体的实例展示了MATLAB在数学建模中的强大功能。通过这些实例,读者可以了解如何使用MATLAB构建、求解和分析数学模型。掌握这些技巧,不仅有助于解决实际问题,还能提升对复杂系统的理解和分析能力。
参考文献与学习资源
-
MATLAB官方文档:提供详尽的函数说明和示例。
https://www.mathworks.com/help/matlab/ -
《MATLAB数学建模方法与实践》,李明著,清华大学出版社。
-
《数学建模算法与应用》,谢金星等著,高等教育出版社。
-
在线课程:Coursera、edX等平台提供的MATLAB和数学建模课程。
-
MathWorks官方示例:涵盖各领域的MATLAB应用示例。
https://www.mathworks.com/examples/

相关文章:

MATLAB 在数学建模中的深入应用:从基础到高级实践
目录 前言 一、MATLAB基础知识 1.1 MATLAB工作环境简介 1.1.1 命令窗口(Command Window) 1.1.2 工作区(Workspace) 1.1.3 命令历史(Command History) 1.1.4 编辑器(Editor) 1…...

Unity 设计模式 之 【什么是设计模式】/ 【为什么要使用设计模式】/ 【架构和设计模式的区别】
Unity 设计模式 之 【什么是设计模式】/ 【为什么要使用设计模式】/ 【架构和设计模式的区别】 目录 Unity 设计模式 之 【什么是设计模式】/ 【为什么要使用设计模式】/ 【架构和设计模式的区别】 一、简单介绍 二、 Unity 设计模式 1、Unity 开发中使用设计模式的特点 2…...

[数据集][目标检测]智慧交通铁路异物入侵检测数据集VOC+YOLO格式802张7类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):802 标注数量(xml文件个数):802 标注数量(txt文件个数):802 标注类别…...

飞驰云联FTP替代方案:安全高效文件传输的新选择
FTP协议广泛应用各行业的文件传输场景中,由于FTP应用获取门槛低、使用普遍,因此大部分企业都习惯使用FTP进行文件传输。然而面临激增的数据量和网络安全威胁的不断演变,FTP在传输安全性与传输性能上有所欠缺,无法满足企业现在的高…...

Hive内置集合函数-size,map_keys,map_values,sort_array,array_contains
1. Hive内置Collection Functions 以下函数为Hive是提供的内置集合函数: 返回类型函数(签名)函数说明intsize(Map<K.V>)Returns the number of elements in the map type.intsize(Array)Returns the number of elements in the array type.arraymap_keys(Map<K.V>…...

Exchange Online 计划 2 部署方案
目录 前言 一、前期准备 1. 了解 Exchange Online 计划 2 的功能 2. 系统要求 3. 网络要求 4. 账户和许可 二、安装和配置 Exchange Online 计划 2 1. 注册 Microsoft 365 订阅 2. 验证域 3. 用户和许可证分配 4. 迁移现有邮箱 迁移步骤 三、配置 Exchange Online …...
图数据库的力量:深入理解与应用 Neo4j
图数据库的力量:深入理解与应用 Neo4j 文章目录 图数据库的力量:深入理解与应用 Neo4j1、什么是 Neo4j?版本说明 2、Neo4j 的部署和安装Neo4j Web 工具介绍 3、体验 Neo4j加载数据查询数据数据结构 4、Cypher 入门创建数据查询数据关系深度查…...

Deutsch intensiv C1 Schreiben
Deutsch intensiv C1 Schreiben Part A1, Kasten Part A 1, Kasten (1)zeigt (A) (2)gibt Auskunft ber (A)/darber (3)liefert Daten/Informationen ber(A)/darber (4)stellt(A) dar...

大数据新视界 --大数据大厂之DevOps与大数据:加速数据驱动的业务发展
💖💖💖亲爱的朋友们,热烈欢迎你们来到 青云交的博客!能与你们在此邂逅,我满心欢喜,深感无比荣幸。在这个瞬息万变的时代,我们每个人都在苦苦追寻一处能让心灵安然栖息的港湾。而 我的…...

实战OpenCV之图像阈值处理
基础入门 图像阈值处理是一种二值化技术,它基于预设的阈值,可以将图像中的像素分为两大类:一大类是背景,另一大类是前景或目标对象。这个过程涉及将图像中的每个像素值与阈值进行比较,并根据比较结果决定保留原始值还是…...

登录后继续执行方法
场景 点击按钮,检测到未登录,直接跳转到登录页,登录成功后,返回页面继续执行刚才的点击事件 思路 在跳转时用一个队列存储该事件,登录成功后执行队列里的事件 队列 class Queue {constructor() {this.task []}cl…...

JVM-类加载器的双亲委派模型详解
JVM中存在三个默认的类加载器: BootstrapClassLoaderExtClassLoaderAppClassLoader AppClassLoader的父加载器是ExtClassLoader,ExtClassLoader的父加载器是 BootstrapClassLoader。 它们之间的关系是:AppClassLoader->ExtClassLoader-&…...

【计算机基础题目】Linux系统中文件权限 字母权限和数字权限的相互转换
创作日志: 很久之前对这个略有了解,但是现在完全忘记了,看到这类题目一脸懵逼,现在系统复习下。 1、权限的数字表示(3位) 在Linux系统中,文件权限由一个三位的八进制数表示,每一位代…...

VRRP协议原理
目录 VRRP概述 VRRP产生背景 VRRP介绍 VRRP相关概念 VRRP报文 VRRP的三种状态 VRRP工作原理 优先级和抢占 VRRP接口跟踪 VRRP概述 VRRP产生背景 通常同一网段内的所有主机都会配置相同的网关,以访问外部网络 当唯一的网关设备发生故障时,所有主…...

Dockerfile自定义制作镜像,其中10个指令的作用分析
docker容器中 做镜像是重要的技能。 docker commit只能制作比较简单的镜像, 要制作比较完善的镜像, 自定义程度比较高的, 就需要用到dockerfile dockerfile可以回溯历史 动态生成镜像。 FROM是基础镜像 CMD是在容器创建的时候默认的启动命令 …...

Linux6-vi/vim
1.vi与vim vi是Linux操作系统下的标准编辑器,类似Windows下的记事本 vim是vi的升级版,包括vi的所有功能,而且支持shell 2.vi/vim下的三种模式 vi/vim有三种模式:命令模式,插入模式和底行模式 命令模式:…...

2012年408考研真题-数据结构
8.【2012统考真题】求整数n(n≥0)的阶乘的算法如下,其时间复杂度是()。 int fact(int n){ if(n<1) return 1; return n*fact (n-1); } A. O(log2n) B. O(n) C. O(nlog2n) D. O(n^2) 解析: 观察代码,我们不…...

【北京迅为】《STM32MP157开发板使用手册》- 第四十章 二值信号量实验
iTOP-STM32MP157开发板采用ST推出的双核cortex-A7单核cortex-M4异构处理器,既可用Linux、又可以用于STM32单片机开发。开发板采用核心板底板结构,主频650M、1G内存、8G存储,核心板采用工业级板对板连接器,高可靠,牢固耐…...

Docker UI强大之处?
DockerUI是一款由国内开发者打造的优秀Docker可视化管理工具。它拥有简洁直观的用户界面,使得Docker主机管理、集群管理和任务编排变得轻松简单。DockerUI不仅能展示资源利用率、系统信息和更新日志,还提供了镜像管理功能,帮助用户高效清理中…...

前端面试题——token安全问题处理与大数据列表展示
1.长时间保存token问题 长时间保存Token涉及多个方面的问题,包括安全性、性能、以及Token的管理策略等。以下是对长时间保存Token问题的详细分析: 一、安全性问题 Token泄露风险: Token是用户身份验证的凭证,如果长时间保存且未…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
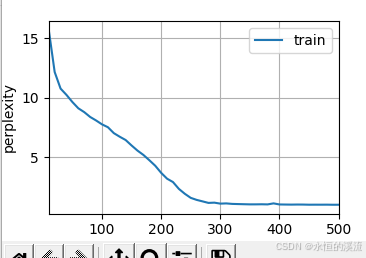
李沐--动手学深度学习--GRU
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...
