SS-MUSIC
SS-MUSIC
- 相干信号源带来的缺秩问题
- 什么是中心对称阵列
- 什么是前后向平均技术
- 什么是 SS-MUSIC 算法
- SS-MUSIC 能解相干的原因
- SS-MUSIC 改进算法
- 总结
- 参考文献
本文讨论针对一维均匀线阵(ULA,Uniform Linear Array)的空间平滑 MUSIC(SS-MUSIC,Spatial Smoothing MUSIC)算法12,同时为了方便公式推导,后续的模型建立在无噪环境下。
相干信号源带来的缺秩问题
假设 K > 1 K>1 K>1 个信号源为同一组完全相干的信号源,即 s k ( t ) = c k s 1 ( t ) s_k(t) = c_ks_1(t) sk(t)=cks1(t),其中 k = 2 , ⋯ , K k = 2,\cdots,K k=2,⋯,K 以及 t = 1 , ⋯ , T t = 1,\cdots,T t=1,⋯,T。令 c = [ 1 , c 2 , ⋯ , c K ] T ∈ C K × 1 \mathbf{c} = [1,c_2,\cdots,c_K]^T\in\mathbb{C}^{K\times 1} c=[1,c2,⋯,cK]T∈CK×1 可得到:
R s = 1 T S S H = 1 T c s 1 s 1 H c H = σ 1 2 c c H \begin{aligned} \mathbf{R}_{\mathrm{s}}&=\frac{1}{T}\mathbf{S}\mathbf{S}^H\\ &=\frac{1}{T}\mathbf{c}\mathbf{s}_1\mathbf{s}_1^H\mathbf{c}^H\\ &=\sigma_1^2\mathbf{c}\mathbf{c}^H \end{aligned} Rs=T1SSH=T1cs1s1HcH=σ12ccH
其中 s 1 ∈ C 1 × T \mathbf{s}_1\in\mathbb{C}^{1\times T} s1∈C1×T 代表第一个阵元的采样序列。为了简化后续推导,我们令 σ 1 2 = 1 \sigma_1^2=1 σ12=1 即可得到 R s = c c H ∈ C K × K \mathbf{R}_{\mathrm{s}} = \mathbf{c}\mathbf{c}^H\in\mathbb{C}^{K\times K} Rs=ccH∈CK×K,因此 r a n k ( R s ) = 1 < K \mathrm{rank}(\mathbf{R}_{\mathrm{s}}) = 1 < K rank(Rs)=1<K,即 R s \mathbf{R}_{\mathrm{s}} Rs 不满秩,此时直接对 R = A R s A H \mathbf{R} = \mathbf{A}\mathbf{R}_{\mathrm{s}}\mathbf{A}^H R=ARsAH 进行 MUSIC 估计会失效。
什么是中心对称阵列
中心对称阵列(Centro-Symmetric Array)是指空间中存在一个参考点,使得每个阵元在关于该参考点的对称位置上,都有另一个相对应的阵元。ULA 就是最经典的一维中心对称阵列,对于 ULA 而言,该参考点就是阵列的中心点。假设空间中存在一组由 M M M 个阵元组成的 ULA,其坐标索引为 { 0 , 1 , ⋯ , M − 1 } \{0,1,\cdots,M-1\} {0,1,⋯,M−1},此时方向矢量 a ( φ ) ∈ C M × 1 \mathbf{a}(\varphi)\in\mathbb{C}^{M\times 1} a(φ)∈CM×1 可表示如下:
a ( φ ) = [ 1 e − j φ ⋮ e − j ( M − 1 ) φ ] \mathbf{a}(\varphi) = \begin{bmatrix} 1 \\ e^{-\mathrm{j}\varphi}\\ \vdots \\ e^{-\mathrm{j}(M-1)\varphi} \end{bmatrix} a(φ)= 1e−jφ⋮e−j(M−1)φ
其中 φ = 2 π d sin ( θ ) / λ \varphi = 2\pi d \sin(\theta)/\lambda φ=2πdsin(θ)/λ, d d d 为相邻阵元的间距,以及 λ \lambda λ 为信号波长。方向矢量矩阵 A ∈ C M × K \mathbf{A}\in\mathbb{C}^{M\times K} A∈CM×K 可表示如下:
A = [ a ( φ 1 ) , a ( φ 2 ) , ⋯ , a ( φ K ) ] \mathbf{A} = [\mathbf{a}(\varphi_1),\mathbf{a}(\varphi_2),\cdots,\mathbf{a}(\varphi_K)] A=[a(φ1),a(φ2),⋯,a(φK)]
ULA 的方向矢量 a ( φ ) \mathbf{a}(\varphi) a(φ) 满足下式:
J a ( φ ) = e − j ( M − 1 ) φ a ∗ ( φ ) \mathbf{J}\mathbf{a}(\varphi) = e^{-\mathrm{j}(M-1)\varphi}\mathbf{a}^*(\varphi) Ja(φ)=e−j(M−1)φa∗(φ)
其中 J ∈ R M × M \mathbf{J}\in\mathbb{R}^{M\times M} J∈RM×M 代表反对角矩阵。不难得出 A \mathbf{A} A 满足下式:
J A = A ∗ Φ M − 1 \mathbf{J}\mathbf{A} = \mathbf{A}^*\Phi^{M-1} JA=A∗ΦM−1
其中 Φ ∈ C K × K \Phi\in\mathbb{C}^{K\times K} Φ∈CK×K 为对角矩阵:
Φ = [ e − j φ 1 ⋱ e − j φ K ] \Phi = \begin{bmatrix} e^{-\mathrm{j}\varphi_1} && \\ &\ddots&\\ &&e^{-\mathrm{j}\varphi_K} \end{bmatrix} Φ= e−jφ1⋱e−jφK
什么是前后向平均技术
前后向平均(Forward Backward Averaging)技术针对中心对称阵列,前后向协方差矩阵 R f b \mathbf{R}_{\mathrm{fb}} Rfb 表示如下:
R f b = 1 2 ( R f + R b ) = 1 2 ( R + J R ∗ J ) \mathbf{R}_{\mathrm{fb}} = \frac{1}{2}(\mathbf{R}_{\mathrm{f}}+\mathbf{R}_{\mathrm{b}})=\frac{1}{2}(\mathbf{R}+\mathbf{J}\mathbf{R}^{*}\mathbf{J}) Rfb=21(Rf+Rb)=21(R+JR∗J)
其中 R f = R \mathbf{R}_{\mathrm{f}}=\mathbf{R} Rf=R 和 R b = J R ∗ J \mathbf{R}_{\mathrm{b}} = \mathbf{J}\mathbf{R}^{*}\mathbf{J} Rb=JR∗J 分别表示为前向协方差矩阵和后向协方差矩阵。代入 R = A R s A H \mathbf{R} = \mathbf{A}\mathbf{R}_{\mathrm{s}}\mathbf{A}^{H} R=ARsAH 可得到:
R f b = 1 2 ( A R s A H + J A ∗ R s ∗ A T J ) = 1 2 ( A R s A H + A Φ M − 1 R s ∗ Φ 1 − M A H ) = 1 2 A ( R s + Φ M − 1 R s ∗ Φ 1 − M ) A H = 1 2 A R f b s A H \begin{aligned} \mathbf{R}_{\mathrm{fb}} &= \frac{1}{2}(\mathbf{A}\mathbf{R}_{\mathrm{s}}\mathbf{A}^{H}+\mathbf{J}\mathbf{A}^{*}\mathbf{R}_{\mathrm{s}}^{*}\mathbf{A}^{T}\mathbf{J})\\ &=\frac{1}{2}(\mathbf{A}\mathbf{R}_{\mathrm{s}}\mathbf{A}^{H}+\mathbf{A}\Phi^{M-1}\mathbf{R}_{\mathrm{s}}^{*}\Phi^{1-M}\mathbf{A}^H)\\ &=\frac{1}{2}\mathbf{A}(\mathbf{R}_{\mathrm{s}}+\Phi^{M-1}\mathbf{R}_{\mathrm{s}}^{*}\Phi^{1-M})\mathbf{A}^H\\ &=\frac{1}{2}\mathbf{A}\mathbf{R}_{\mathrm{fbs}}\mathbf{A}^H \end{aligned} Rfb=21(ARsAH+JA∗Rs∗ATJ)=21(ARsAH+AΦM−1Rs∗Φ1−MAH)=21A(Rs+ΦM−1Rs∗Φ1−M)AH=21ARfbsAH
其中 R f b s = R s + Φ M − 1 R s ∗ Φ 1 − M \mathbf{R}_{\mathrm{fbs}}=\mathbf{R}_{\mathrm{s}}+\Phi^{M-1}\mathbf{R}_{\mathrm{s}}^{*}\Phi^{1-M} Rfbs=Rs+ΦM−1Rs∗Φ1−M。同理可得到:
R f s = R s R b s = Φ M − 1 R s ∗ Φ 1 − M \begin{aligned} \mathbf{R}_{\mathrm{fs}}&=\mathbf{R}_{\mathrm{s}} \\ \mathbf{R}_{\mathrm{bs}}&=\Phi^{M-1}\mathbf{R}_{\mathrm{s}}^{*}\Phi^{1-M} \end{aligned} RfsRbs=Rs=ΦM−1Rs∗Φ1−M
从前面相干信号的讨论中,已知 r a n k ( R s ) = 1 \mathrm{rank}(\mathbf{R}_{\mathrm{s}}) = 1 rank(Rs)=1,即 r a n k ( R f s ) = r a n k ( R b s ) = 1 \mathrm{rank}(\mathbf{R}_{\mathrm{fs}}) = \mathrm{rank}(\mathbf{R}_{\mathrm{bs}}) = 1 rank(Rfs)=rank(Rbs)=1,然而 R f b s \mathbf{R}_{\mathrm{fbs}} Rfbs 的秩并不为 1 1 1,具体推导如下:
R f b s = R s + Φ M − 1 R s ∗ Φ 1 − M = I c c H I + Φ M − 1 c c H Φ 1 − M = C 1 1 T C H + C Φ M − 1 Φ M − 1 H C H = C [ 1 Φ M − 1 ] [ 1 T Φ M − 1 H ] C H \begin{aligned} \mathbf{R}_{\mathrm{fbs}}&=\mathbf{R}_{\mathrm{s}}+\Phi^{M-1}\mathbf{R}_{\mathrm{s}}^{*}\Phi^{1-M}\\ &= \mathbf{I}\mathbf{c}\mathbf{c}^H\mathbf{I} + \Phi^{M-1}\mathbf{c}\mathbf{c}^H \Phi^{1-M} \\ &= \mathbf{C} \mathbf{1} \mathbf{1}^T\mathbf{C}^H + \mathbf{C} \varPhi_{M-1} \varPhi_{M-1}^H\mathbf{C}^H \\ &= \mathbf{C} \begin{bmatrix} \mathbf{1} & \varPhi_{M-1} \end{bmatrix} \begin{bmatrix} \mathbf{1}^T \\ \varPhi_{M-1}^H \end{bmatrix} \mathbf{C}^H \end{aligned} Rfbs=Rs+ΦM−1Rs∗Φ1−M=IccHI+ΦM−1ccHΦ1−M=C11TCH+CΦM−1ΦM−1HCH=C[1ΦM−1][1TΦM−1H]CH
其中 C ∈ C K × K \mathbf{C}\in\mathbb{C}^{K\times K} C∈CK×K 代表 c ∈ C K × 1 \mathbf{c}\in\mathbb{C}^{K\times 1} c∈CK×1 的对角形式, Φ M − 1 ∈ C K × 1 \varPhi_{M-1}\in\mathbb{C}^{K\times 1} ΦM−1∈CK×1 代表 Φ M − 1 ∈ C K × K \Phi^{M-1}\in\mathbb{C}^{K\times K} ΦM−1∈CK×K 对角元素的向量形式, I \mathbf{I} I 代表单位矩阵,以及 1 \mathbf{1} 1 代表全 1 1 1 向量。显然 [ 1 Φ M − 1 ] ∈ C K × 2 [\mathbf{1}\,\,\,\,\varPhi_{M-1}]\in\mathbb{C}^{K\times 2} [1ΦM−1]∈CK×2 的列线性无关,因此 r a n k ( R f b s ) = 2 \mathrm{rank}(\mathbf{R}_{\mathrm{fbs}}) = 2 rank(Rfbs)=2。
什么是 SS-MUSIC 算法
SS-MUSIC 算法提出切分子阵列的方式来解相干,首先将原阵列视为阵元数为 M M M 的单个连续阵列,则 SS-MUSIC 将原阵列切分为 N N N 个连续子阵列,其中每个子阵列有 P P P 个阵元。第一个子阵列包括原阵列中前 1 ∼ P 1\sim P 1∼P 个阵元,第二个子阵列包括原阵列中前 2 ∼ P + 1 2\sim P+1 2∼P+1 个阵元。不难看出 M = N + P − 1 M = N+P-1 M=N+P−1。切分阵列后,再通过子阵列的互相关矩阵来进行累加,即可得到空间平滑结果。
SS-MUSIC 又可以细分为 FSS-MUSIC、BSS-MUSIC 和 FBSS-MUSIC,它们分别针对 R f \mathbf{R}_{\mathrm{f}} Rf、 R b \mathbf{R}_{\mathrm{b}} Rb 和 R f b \mathbf{R}_{\mathrm{fb}} Rfb 进行子阵列切分操作,通常情况下 FBSS-MUSIC 是最优选择。FSS-MUSIC、BSS-MUSIC 和 FBSS-MUSIC 的空间平滑结果如下:
R f s s = 1 N ∑ i = 1 N [ R f ] i i R b s s = 1 N ∑ i = 1 N [ R b ] i i R f b s s = 1 N ∑ i = 1 N [ R f b ] i i \begin{aligned} \mathbf{R}_{\mathrm{fss}} &= \frac{1}{N}\sum_{i=1}^{N} [\mathbf{R}_{\mathrm{f}}]_{ii} \\ \mathbf{R}_{\mathrm{bss}} &= \frac{1}{N}\sum_{i=1}^{N} [\mathbf{R}_{\mathrm{b}}]_{ii} \\ \mathbf{R}_{\mathrm{fbss}} &= \frac{1}{N}\sum_{i=1}^{N} [\mathbf{R}_{\mathrm{fb}}]_{ii} \end{aligned} RfssRbssRfbss=N1i=1∑N[Rf]ii=N1i=1∑N[Rb]ii=N1i=1∑N[Rfb]ii
其中 [ R ] i j ∈ C P × P [\mathbf{R}]_{ij}\in\mathbb{C}^{P\times P} [R]ij∈CP×P 表示第 i i i 个子阵列和第 j j j 个子阵列的相关矩阵:
[ R ] i j = A P Φ i − 1 R Φ 1 − j A P H [\mathbf{R}]_{ij} = \mathbf{A}_{\mathrm{P}}\Phi^{i-1}\mathbf{R}\Phi^{1-j}\mathbf{A}_{\mathrm{P}}^H [R]ij=APΦi−1RΦ1−jAPH
其中 i = 1 , ⋯ , N i=1,\cdots,N i=1,⋯,N, j = 1 , ⋯ , N j=1,\cdots,N j=1,⋯,N 且 A P \mathbf{A}_{\mathrm{P}} AP 表示 A \mathbf{A} A 的前 P P P 行。如此得到的 R f s s \mathbf{R}_{\mathrm{fss}} Rfss、 R b s s \mathbf{R}_{\mathrm{bss}} Rbss 和 R f b s s \mathbf{R}_{\mathrm{fbss}} Rfbss 可直接用于 MUSIC 估计。
SS-MUSIC 能解相干的原因
相干信号源带来的问题是信号协方差矩阵 R s \mathbf{R}_{\mathrm{s}} Rs 的秩降低了,因此 SS-MUSIC 的工作便是将 R s \mathbf{R}_{\mathrm{s}} Rs 的秩恢复为 K K K,以 R f s s \mathbf{R}_{\mathrm{fss}} Rfss 为例:
R f s s = 1 N ∑ i = 1 N [ R f ] i i = 1 N ( A P R f s A P H + ⋯ + A P Φ N − 1 R f s Φ 1 − N A P H ) = 1 N A P ( ∑ i = 1 N Φ i − 1 R f s Φ 1 − i ) A P H \begin{aligned} \mathbf{R}_{\mathrm{fss}} &= \frac{1}{N}\sum_{i=1}^{N} [\mathbf{R}_{\mathrm{f}}]_{ii} \\ &=\frac{1}{N} \left(\mathbf{A}_{\mathrm{P}}\mathbf{R}_{\mathrm{fs}}\mathbf{A}_{\mathrm{P}}^H+\cdots+\mathbf{A}_{\mathrm{P}}\Phi^{N-1}\mathbf{R}_{\mathrm{fs}}\Phi^{1-N}\mathbf{A}_{\mathrm{P}}^H\right) \\ &= \frac{1}{N} \mathbf{A}_{\mathrm{P}} \left( \sum_{i=1}^N \Phi^{i-1}\mathbf{R}_{\mathrm{fs}}\Phi^{1-i}\right)\mathbf{A}_{\mathrm{P}}^H \end{aligned} Rfss=N1i=1∑N[Rf]ii=N1(APRfsAPH+⋯+APΦN−1RfsΦ1−NAPH)=N1AP(i=1∑NΦi−1RfsΦ1−i)APH
由于 R f s = c c H \mathbf{R}_{\mathbf{fs}} = \mathbf{c}\mathbf{c}^H Rfs=ccH,我们得到:
Φ i − 1 R f s Φ 1 − i = C Φ i − 1 Φ i − 1 H C H \Phi^{i-1}\mathbf{R}_{\mathrm{fs}}\Phi^{1-i} = \mathbf{C}\varPhi_{i-1}\varPhi_{i-1}^H \mathbf{C}^H Φi−1RfsΦ1−i=CΦi−1Φi−1HCH
其中 C ∈ C K × K \mathbf{C}\in\mathbb{C}^{K\times K} C∈CK×K 代表 c ∈ C K × 1 \mathbf{c}\in\mathbb{C}^{K\times 1} c∈CK×1 的对角形式, Φ i − 1 ∈ C K × 1 \varPhi_{i-1}\in\mathbb{C}^{K\times 1} Φi−1∈CK×1 代表 Φ i − 1 ∈ C K × K \Phi^{i-1}\in\mathbb{C}^{K\times K} Φi−1∈CK×K 对角元素的向量形式。
进一步化简:
R f s s = 1 N A P ( ∑ i = 1 N Φ i − 1 R f s Φ 1 − i ) A P H = 1 N A P C ( ∑ i = 1 N Φ i − 1 Φ i − 1 H ) C H A P H = 1 N A P C A N H A N C H A P H \begin{aligned} \mathbf{R}_{\mathrm{fss}} &=\frac{1}{N} \mathbf{A}_{\mathrm{P}} \left( \sum_{i=1}^N \Phi^{i-1}\mathbf{R}_{\mathrm{fs}}\Phi^{1-i}\right)\mathbf{A}_{\mathrm{P}}^H \\ &= \frac{1}{N} \mathbf{A}_{\mathrm{P}} \mathbf{C}\left( \sum_{i=1}^N \varPhi_{i-1}\varPhi_{i-1}^H\right) \mathbf{C}^H\mathbf{A}_{\mathrm{P}}^H\\ &=\frac{1}{N} \mathbf{A}_{\mathrm{P}} \mathbf{C} \mathbf{A}_{\mathrm{N}}^H\mathbf{A}_{\mathrm{N}} \mathbf{C}^H\mathbf{A}_{\mathrm{P}}^H \end{aligned} Rfss=N1AP(i=1∑NΦi−1RfsΦ1−i)APH=N1APC(i=1∑NΦi−1Φi−1H)CHAPH=N1APCANHANCHAPH
其中 A N ∈ C N × K \mathbf{A}_{\mathrm{N}}\in\mathbb{C}^{N\times K} AN∈CN×K 代表 A \mathbf{A} A 的前 N N N 行。通过对 R f s s \mathbf{R}_{\mathrm{fss}} Rfss 的推导,我们不难得出结论:每一次的累加,均使得 R f s s \mathbf{R}_{\mathrm{fss}} Rfss 的秩恢复 r a n k ( R f s ) = 1 \mathrm{rank}(\mathbf{R}_{\mathrm{fs}}) = 1 rank(Rfs)=1 个,故而最后 r a n k ( R f s s ) = min ( P − 1 , N , K ) \mathrm{rank}(\mathbf{R}_{\mathrm{fss}}) = \min(P-1,N,K) rank(Rfss)=min(P−1,N,K)。因此为了让 R f s s \mathbf{R}_{\mathrm{fss}} Rfss 的秩恢复为 K K K,需要保证 N ≥ K N\geq K N≥K 和 P > K P>K P>K 成立。结合 M = N + P − 1 M = N+P-1 M=N+P−1 我们将得到:
K ≤ 1 2 M K\leq\frac{1}{2}M K≤21M
即 FSS-MUSIC 至多能估计 1 2 M \frac{1}{2}M 21M 个同组的相干信号源。同理 BSS-MUSIC 也一样。
相比于 FSS-MUSIC 和 BSS-MUSIC,FBSS-MUSIC 有更高的自由度。每一次的累加,均使得 R f b s s \mathbf{R}_{\mathrm{fbss}} Rfbss 的秩恢复 r a n k ( R f b s ) = 2 \mathrm{rank}(\mathbf{R}_{\mathrm{fbs}}) = 2 rank(Rfbs)=2 个,故而最后 r a n k ( R f b s s ) = min ( P − 1 , 2 N , K ) \mathrm{rank}(\mathbf{R}_{\mathrm{fbss}}) = \min(P-1,2N,K) rank(Rfbss)=min(P−1,2N,K)。因此为了让 R f b s s \mathbf{R}_{\mathrm{fbss}} Rfbss 的秩恢复为 K K K,需要保证 2 N ≥ K 2N\geq K 2N≥K 和 P > K P>K P>K 成立。结合 M = N + P − 1 M = N+P-1 M=N+P−1 我们将得到:
K ≤ 2 3 M K\leq\frac{2}{3}M K≤32M
即 FBSS-MUSIC 至多能估计 2 3 M \frac{2}{3}M 32M 个同组的相干信号源。
SS-MUSIC 改进算法
实质上,SS-MUSIC 将协方差矩阵 R \mathbf{R} R 进行分块,并取属于对角位置的子矩阵进行累加,只要累加的次数足够,即可将内部信号协方差的秩恢复为 K K K。IFBSS-MUSIC3(Improved FBSS-MUSIC)利用非对角位置的子矩阵进行计算:
R i f b s s = 1 N 2 ∑ i = 1 N ∑ j = 1 N [ R f b ] i j [ R f b ] j i \mathbf{R}_{\mathrm{ifbss}} = \frac{1}{N^2}\sum_{i=1}^{N}\sum_{j=1}^{N} [\mathbf{R}_{\mathrm{fb}}]_{ij}[\mathbf{R}_{\mathrm{fb}}]_{ji} Rifbss=N21i=1∑Nj=1∑N[Rfb]ij[Rfb]ji
进一步可得到:
R i f b s s = 1 N 2 A P [ ∑ i = 1 N Φ i − 1 R f b s ( ∑ j = 1 N Φ 1 − j A P H A P Φ j − 1 ) R f b s Φ 1 − i ] A P H \begin{aligned} \mathbf{R}_{\mathrm{ifbss}} = \frac{1}{N^2}\mathbf{A}_{\mathrm{P}}\left[\sum_{i=1}^{N} \Phi^{i-1} \mathbf{R}_{\mathrm{fbs}}\left( \sum_{j=1}^{N} \Phi^{1-j}\mathbf{A}_{\mathrm{P}}^H\mathbf{A}_{\mathrm{P}}\Phi^{j-1}\right)\mathbf{R}_{\mathrm{fbs}}\Phi^{1-i}\right]\mathbf{A}_{\mathrm{P}}^H \end{aligned} Rifbss=N21AP[i=1∑NΦi−1Rfbs(j=1∑NΦ1−jAPHAPΦj−1)RfbsΦ1−i]APH
总结
总的来说,SS-MUSIC 针对于 ULA 实现,而 ULA 属于中心对称阵列,因此结合前后向平均技术可以进一步提升自由度。从上面的讨论可得知,当 K > 1 K>1 K>1 个信号源同属一组相干源,即原协方差矩阵秩为 1 1 1,前后向平均技术可以实现一定的解相干,即将协方差矩阵的秩恢复为 2 2 2,但解相干能力有限。SS-MUSIC 牺牲了阵列孔径,但能实现完全解相干。
参考文献
Shan T J, Wax M, Kailath T. On spatial smoothing for direction-of-arrival estimation of coherent signals[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1985, 33(4): 806-811. ↩︎
Pillai S U, Kwon B H. Forward/backward spatial smoothing techniques for coherent signal identification[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(1): 8-15. ↩︎
Du W, Kirlin R L. Improved spatial smoothing techniques for DOA estimation of coherent signals[J]. IEEE Transactions on signal processing, 1991, 39(5): 1208-1210. ↩︎
相关文章:

SS-MUSIC
SS-MUSIC 相干信号源带来的缺秩问题什么是中心对称阵列什么是前后向平均技术什么是 SS-MUSIC 算法SS-MUSIC 能解相干的原因SS-MUSIC 改进算法总结参考文献 本文讨论针对一维均匀线阵(ULA,Uniform Linear Array)的空间平滑 MUSIC(S…...

Spring Cloud Gateway组件
Spring Cloud Gateway是Spring Cloud生态系统中的一个关键组件,它基于Spring Framework 5、Spring Boot 2和Project Reactor等技 术构建,为微服务架构提供了强大且灵活的网关服务。以下是对Spring Cloud Gateway的详细介绍:一、概述 Spring …...

激发AI创造力:掌握Prompt提示词的高效提问方法
AI内容创作的核心:提示词Prompt 在AI内容创作中,提示词(Prompt)是关键因素,能有效引导AI生成高质量、符合预期的内容。通过合理组织提示词,创作者可以大幅提升AI输出的准确性和专业度。掌握提示词的编写技…...

江科大笔记—STM32课程简介
课程简介...
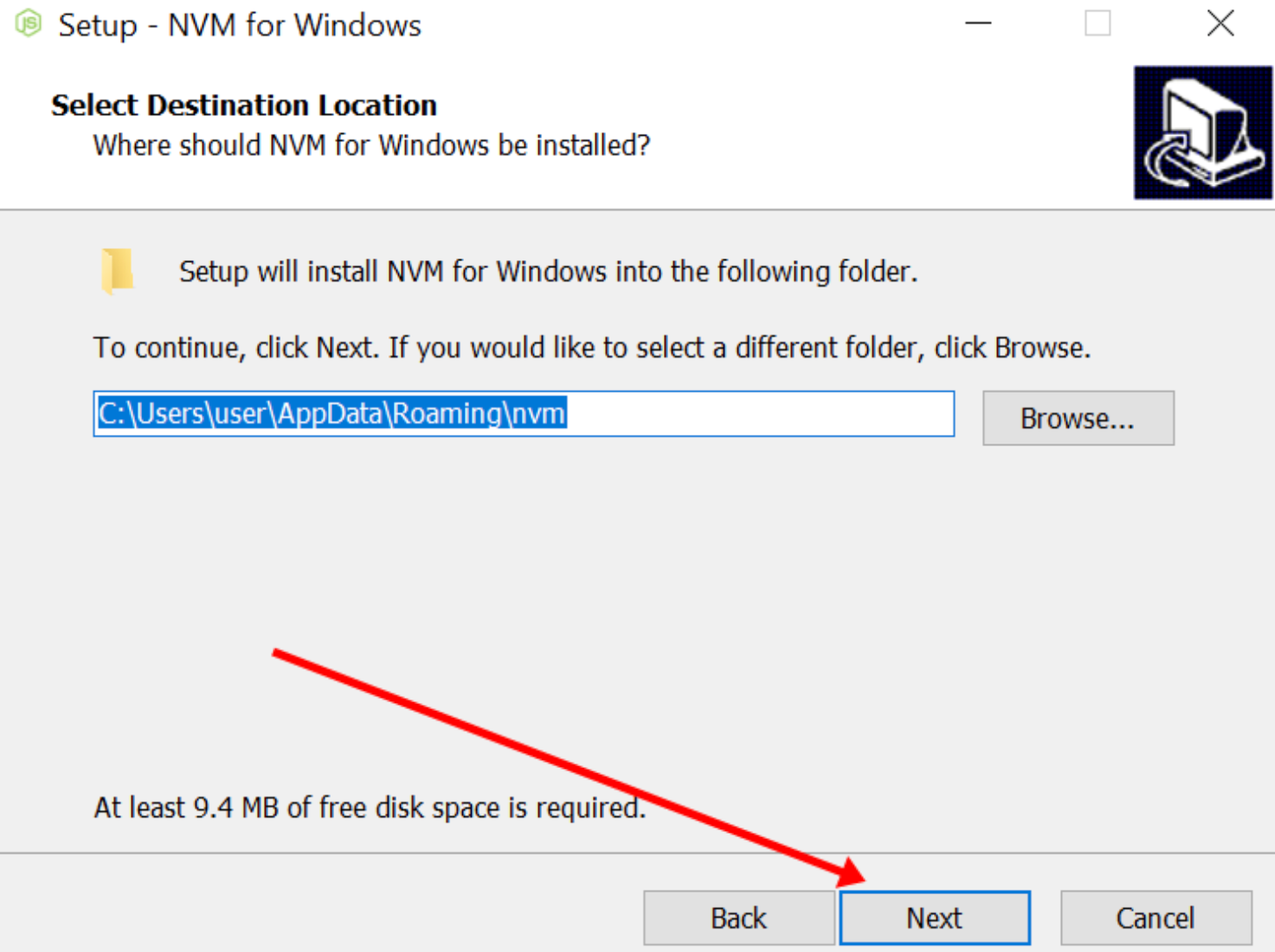
使用 nvm 管理 node 版本:如何在 macOS 和 Windows 上安装使用nvm
🔥 个人主页:空白诗 文章目录 一、引言二、nvm的安装与基本使用2.1 macOS安装nvm2.1.1 使用 curl 安装2.1.2 使用 Homebrew 安装 2.2 Windows安装nvm2.2.1 下载 nvm-windows2.2.2 安装 nvm-windows 2.3 安装node2.4 切换node版本 三、常见问题及解决方案…...

【项目开发 | Python】基于“羊了个羊“风格的消除类小游戏
原创文章,不得转载。 目标:使用 Python 开发"羊了个羊"风格的消除类小游戏,合理运用 AIGC 工具提高开发效率;使用文生图工具实现图片设计等工作。 文章目录 项目背景项目介绍+项目展示游戏逻辑概述主界面游戏界面获胜界面失败界面附加功能项目细节项目测试测试样…...

云服务器使用
最近搭建一个内网穿透工具,推荐一个云服务器: 三丰台:https://www.sanfengyun.com/ 作为学生党这个服务器是免费的可以体验使用!可以使用免费虚拟主机和云服务器,写一个申请的基本步骤方便大家构建 申请步骤&#x…...

sqli-lab靶场学习(四)——Less11-14(post方法)
前言 第1-10关都是get方法,本关开始进入post方法。其实post也好get也好,本质都差不多,使用的技巧也基本相同。 Less11 第11关打开是一个输入用户名密码的界面 显然登陆对话框会使用post方式提交,这里我们尝试在Username一栏通过…...

GBDT算法原理及其公式推导过程
GBDT(Gradient Boosting Decision Tree,梯度提升决策树)是一种集成学习方法,主要用于回归和分类任务。它的基本思想是通过迭代地构建一系列弱学习器(通常是决策树),并将这些弱学习器组合成一个强…...

网络:UDP协议
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》《Linux》 文章目录 前言UDP协议报头和有效载荷分离的问题有效载荷向上交付的问题,也就是交给哪个进程?怎么确定把报文收全了?UDP报头是如何封装的呢&…...

linux与unix
不同点 1开源性 linux是开源的,unix是闭源的 2跨平台性 linux具有很好的跨平台性,可以运行在多种硬件平台 unix大多需要与指定硬件配套使用 3相关操作 linux既可以进行命令行操作,也可以进行图形化的操作 unix只是命令行下的操作 4对…...

计算机网络29——Linux基本命令vim,gcc编译命令
1、创建新用户 2、给用户设置密码 3、切换到新用户 切换到root用户 4、删除用户 5、查看ip 6、ping 查看物理上两台主机是否联通 7、netstatus 8、nslookup 查看网址的地址 9、负载均衡与容灾备份 负载均衡:指将负载(工作任务)进行平衡、分…...

uniapp离线(本地)打包
安卓离线打包 注意:jdk建议选择1.8 下载Android Studio配置gradle仓库地址 第一步:先下载对应的版本,进行压缩包解压 第二步:在电脑磁盘(D盘),创建文件夹存放压缩包并进行解压,并创…...

如何编写一个爬虫以实时获取某平台商品价格
编写一个爬虫来实时获取某个平台的商品价格是一项实用的任务,可以帮助用户了解市场动态或监控价格变化。以下是一个简单的爬虫示例,使用 Python 的 requests 和 BeautifulSoup 库来抓取商品价格。为了演示,我将以一个假设的电商网站为例&…...

声网SDK脚本运行错误
文章目录 运行步骤无法运行.bat电脑出现警告--更改执行策略若无出现-更新power shell搜索最新版本的 PowerShell安装新版本 仍无法解决-手动下载第三方库 2024-9-9运行步骤 无法运行.bat 电脑出现警告–更改执行策略 若无出现-更新power shell 搜索最新版本的 PowerShell 在…...

Docker + Win 10 学习记录
下载Docker Release notes | Docker Docs 推荐使用4.33版本,最新的Docker版本在win10 22H2无法安装。需要升级到win11. 查看Win10版本是否与最新版的Docker兼容 运行 win R, 然后输入winver 如果你的Docker版本无法在当前的win10安装,请更…...

GlusterFS分布式存储
目录 一、GlusterFS分布式存储概述 1、GFS概念 2、GFS特点 3、GFS术语 4、GFS架构 5、GFS工作流程 6、GlusterFs的卷类型 6.1、 分布式卷(Distributed Volume) 6.2、条带卷(Striped Volume) 6.3、复制卷(Rep…...
:绿盟科技)
ARM/Linux嵌入式面经(三八):绿盟科技
文章目录 @[toc]堆和栈是怎么实现的?基本概念实现方式栈的实现堆的实现面试官的追问堆和栈的运用是怎样运用的、怎样存储的?回答栈(Stack)堆(Heap)深度对比面试官可能的追问Linux系统中进程与进程之间的通信方式有哪些?1. 管道(Pipe)2. 共享内存(Shared Memory)3. 消…...

C#的数据类型转换
目录 C#的数据类型转换 1.隐式转换 2.显式转换 3.Convert类 4.字符串解析 本篇文章来分享一下C#的数据类型转换,主要包括四种方法:隐式转换、显式转换、Convert类、字符串解析。 C#的数据类型转换 1.隐式转换 隐式转换是在不丢失数据的情况下由编译…...

Oracle重做日志文件的添加及删除
在Oracle数据库中,添加和删除日志组文件是数据库维护中的常见操作,它们对于数据库的恢复能力和性能都有重要影响。以下是关于如何在Oracle中添加和删除日志组文件的详细步骤: 一、添加日志组文件 添加日志组文件是为了增加数据库的冗余度和…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
