数据结构与算法——Java实现 6.递归
要学会试着安静下来
—— 24.9.17
一、递归的定义
计算机科学中,递归是一种解决计算问题的方法,其中解决方案取决于同一类问题的更小子集
说明:
① 自己调用自己,如果说每个函数对应着一种解决方案,自己调用自己意味着解决方案是一样的(有规律的)
② 每次调用,函数处理的数据会较上次缩减(子集),而且最后会缩减至无需继续递归
③ 内层函数调用(子集处理)完成,外层函数才能算调用完成(内层完成,外层才能完成——先处理子问题)
二、递归的解题思路
1.确定能否使用递归求解
2.推导出递推关系,即父问题与子问题的关系,以及递归的结束条件
① 深入到最里层叫递
② 从最里层出来叫归
③ 在递的过程中,外层函数内的局部变量(以及方法参数)并未消失,归的时候还可以用到
④ 大问题慢慢递到小问题,再从小问题计算结果归回大问题
⑤ 递的时候是顺序的,归的时候是逆序的
三、递归——习题
1.阶乘
用递归的方法求阶乘
阶乘的定义:n! = 1*2*.3*(n-2)*(n-1)*n,其中n为自然数,当然0! = 1
递推关系:f(n) = 1,n = 1;f(n) = n * f(n-1), n > 1
public class demo1Factorial {// 递归函数public static int factorial(int n) {if (n == 1){return 1;}return n * factorial(n-1);}public static void main(String[] args) {demo1Factorial demo1Factorial = new demo1Factorial();System.out.println(demo1Factorial.factorial(5));System.out.println(factorial(6));System.out.println(factorial(7));System.out.println(factorial(8));}
}

2.反向打印字符串
用递归反向打印字符串,n为字符在整个字符串 str 中的索引位置。
递:n从0开始,每次n+1,一直递到n == str.length()-1。
归:从n==str.length()开始归,从归打印,自然是逆序的
递推关系:f(m)=1rn1)osns.h()-1n=str.length()
注:因为是先递再归,所以反向打印字符串输出语句的位置应该放在调用递归函数之后
public class demo2ReversePrintStr {// 静态方法反向打印字符串public static void reversePrintStr(String str,int n) {if (n == str.length()){return;}// System.out.print(str.charAt(n)+" ");reversePrintStr(str,n+1);System.out.print(str.charAt(n)+" ");}public static void main(String[] args) {reversePrintStr("YYSHlcl",0);}
}
3.二分查找
输入元素,返回元素在有序数组中的位置
前提:待查找数组是有序数组
public class demo3BinarySearch {public static int binarySearch(int[] arr, int key) {int target = Finding(arr,key,0,arr.length-1);return target;}private static int Finding(int[] arr, int key,int i,int j) {if (i > j){return -1;}int m = (i + j) >>> 1;if (key == arr[m]) {return m;}else if (key < arr[m]) {j = m-1;return Finding(arr,key,i,j);}else {i = m+1;return Finding(arr,key,i,j);}}public static void main(String[] args) {int[] arr = {7,9,11,12,24,34,65,81,98};int res = binarySearch(arr, 81);System.out.println("结果为:"+res);System.out.println(binarySearch(arr, 7));System.out.println(binarySearch(arr, 9));System.out.println(binarySearch(arr, 81));}
}

4.递归冒泡排序
将数组划分成两部分 [0…j][j+1…a.length-1]
左边 [0…j] 是未排序部分
右边 [j+1…a.length-1]是已排序部分
未排序区间内,相邻的两个元素比较,如果前一个大于后一个,则交换位置
package Day7Recursion;import java.util.Arrays;public class demo4BubbleSort {public static void sort(int[] arr) {bubble(arr,arr.length-1);}// j代表未排序区域的右边界private static void bubble(int[] arr, int j) {if (j == 0){return;}for (int i = 0; i < j; i++) {if (arr[i] > arr[i + 1]) {int temp = arr[i];arr[i] = arr[i + 1];arr[i + 1] = temp;}}bubble(arr, j - 1);}public static void main(String[] args) {int[] arr = { 5, 4, 3, 2, 1 };System.out.println(Arrays.toString(arr));bubble(arr,arr.length-1);System.out.println(Arrays.toString(arr));sort(arr);System.out.println(Arrays.toString(arr));}
}

将已排序的部分省略,提高效率
private static void adbubble(int[] arr, int j) {if (j == 0){return;}int x = 0;for (int i = 0; i < j; i++) {if (arr[i] > arr[i + 1]) {int temp = arr[i];arr[i] = arr[i + 1];arr[i + 1] = temp;x = i;}}adbubble(arr,x);}
5.插入排序
插入排序(Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,找到排序位置后,需要将已排序元素逐步向后挪位,为最新元素提供插入空间。
插入排序:将元素放在一个已排序的元素队列中,使其仍然有序,类比于扑克牌,将插入位置找到后,插入元素
import java.util.Arrays;public class demo5InsertSort {public static void sort(int[] arr) {insertSort(arr,1);}// low代表未排序区域的下边界private static void insertSort(int[] arr,int low) {// 代表所有元素都已经被排序if (low == arr.length) {return;}int t = arr[low];int i = low - 1; // 已排序区域指针while (i >= 0 && arr[i] > t){ // 循环找到插入位置arr[i+1] = arr[i];i--;}// 找到插入位置arr[i+1] = t;insertSort(arr,low+1);}public static void main(String[] args) {int[] arr = {111,27,36,45,51,63,7,81,9};sort(arr);System.out.println(Arrays.toString(arr));}
}

四、多路递归
上面写到的递归都是只调用了一次递归函数,我们也称之为单路递归
如果每个递归函数包含多个自身的调用,我们称之为多路递归
1.斐波那契数列
思路:多路进行递归,将问题转化为子问题,逐步小化问题

public class demo1MoreFib {public static int fib(int n) {if (n==0){return 0;}if (n==1){return 1;}int x = fib(n-1);int y = fib(n-2);return x + y;}public static void main(String[] args) {int fib = fib(9);System.out.println("第九项斐波那契数列返回结果为:"+fib);}
}

斐波那契数列的时间复杂度推导:

2.兔子问题
第一个月,有一对未成熟的兔子
第二个月,它们成熟
第三个月,它们能产下一对新的小兔子
所有兔子遵循相同规律,求第n 个月的兔子数
注意:注意停止迭代条件与开始数列条件,与斐波那契数列的变化
import java.util.Scanner;public class demo2FibRabbit {public static int fib(int n) {if (n==1||n==2){return 1;}return fib(n-1)+fib(n-2);}public static void main(String[] args) {System.out.println("请您输入你想要得知的月份:");Scanner sc = new Scanner(System.in);int month = sc.nextInt();int rab = fib(month);System.out.println("第"+month+"月的小兔子有"+rab+"只");}
}

3.青蛙爬楼梯
楼梯有 n. 阶
青蛙要爬到楼顶,可以一次跳一阶,也可以一次跳两阶
只能向上跳,问有多少种跳法
import java.util.Scanner;public class demo3frag {public static int fibFrag(int n) {if (n == 1){return 1;}if (n == 2){return 2;}return fibFrag(n-1) + fibFrag(n-2);}public static void main(String[] args) {Scanner sc = new Scanner(System.in);System.out.println("请输入您想要让青蛙上几楼");int n = sc.nextInt();int method = fibFrag(n);System.out.println("共用"+method+"种跳法");}
}

4.汉诺塔问题
Tower of Hanoi,是一个源于印度古老传说:大梵天创建世界时做了三根金刚石柱,在一根柱子从下往上按大小顺序摞着 64 片黄金圆盘,大梵天命令婆罗门把圆盘重新摆放在另一根柱子上,并且规定:
① 一次只能移动一个圆盘
② 小圆盘上不能放大圆盘
思路
① 一个圆盘:圆盘1:a——>c
② 两个圆盘:圆盘1:a——>b、圆盘2:a——>c、圆盘1:b——>c
③ 三个圆盘:圆盘12:a——>b、圆盘3:a——>c、圆盘12:b——>c
④ 四个圆盘:圆盘123:a——>b、圆盘4:a——>c、圆盘123:b——>c
时间复杂度计算:T(n) = 2T(n-1) + c,T(1) = c
T(n) = c(2^n-1)
import java.util.LinkedList;public class demo4HanoiTower {// 三个LinkedList集合代表三根柱子static LinkedList<Integer> a = new LinkedList<>();static LinkedList<Integer> b = new LinkedList<>();static LinkedList<Integer> c = new LinkedList<>();// 类似于添加元素放到柱子上// 初始化柱子static void init(int n){for (int i = n; i >= 1 ; i--) {a.addLast(i);}}// 设计递归函数 n:圆盘个数 a:原始柱子 b:借用柱子 c:目标柱子static void move(int n,LinkedList<Integer> a,LinkedList<Integer> b,LinkedList<Integer> c){if (n==0){return;}// 将n-1个盘子由a借助c移动到b上move(n - 1, a, c, b);c.addLast(a.removeLast()); // 中间步骤Print();// 将n-1个盘子由b借用a移动到c上move(n - 1, b, a, c);}public static void Print(){System.out.println("————————————————————————");System.out.println(a);System.out.println(b);System.out.println(c);}public static void main(String[] args) {init(3);Print();move(3,a,b,c);}// 时间复杂度计算:T(n) = 2T(n-1) + c,T(1) = c// T(n) = c(2^n-1)
}

5.杨辉三角
分析
行i,列j,那么[i][j]的取值应该为[ i-1 ][ j-1 ] + [ i-1 ][ j ]
当 j = 0 或 i = j 时,[ i ][ j ]的取值为-1
public class demo5YangHui {public static int element(int i,int j){if (j == 0||j == i){return 1;}return element(i - 1,j - 1)+element(i - 1,j);}// 打印空格private static void printSpace(int n,int i){int num = (n - 1 - i) * 2;for (int j = 0; j < num; j++) {System.out.print(" ");}}public static void Print(int n){for (int i = 0; i < n; i++) {printSpace(n,i);for (int j = 0; j <= i; j++) {System.out.printf("%-4d",element(i,j));}System.out.println();}}public static void main(String[] args) {Print(9);}}

6.杨辉三角——改进版1
用一个二维数组接收上次遍历的杨辉三角的数值,然后根据上一行的数据进行相加
用二维数组的空间复杂度换取递归的时间复杂度
public class demo6YangHuiEx1 {// 记忆法利用二维数组进行缓存,优化public static int element(int[][] triangle,int i,int j){if (triangle[i][j] > 0){return triangle[i][j];}if (j == 0 || i == j){triangle[i][j] = 1;return 1;}triangle[i][j] = element( triangle,i - 1,j - 1) + element(triangle,i - 1, j);return triangle[i][j];}// 打印空格 空格与高度和行号有关private static void printSpace(int n,int i){int num = (n - 1 - i) * 2;for (int j = 0; j < num; j++) {System.out.print(" ");}}public static void Print(int n){int[][] triangle = new int[n][];for (int i = 0; i < n; i++) {triangle[i] = new int[i+1];// 空格与高度和行号有关printSpace(n,i);for (int j = 0; j <= i; j++) {// 格式化输出 宽度为4 从左对齐System.out.printf("%-4d",element(triangle,i,j));}System.out.println();}}public static void main(String[] args) {Print(5);}
}

7.杨辉三角——改进版2
利用一维数组记忆存储,用少量的空间复杂度换取递归的时间复杂度
这种算法也称为动态规划算法
public class demo7YangHuiEx2 {// 记忆法利用一维数组进行缓存,优化// 打印空格 空格与高度和行号有关private static void printSpace(int n,int i){int num = (n - 1 - i) * 2;for (int j = 0; j < num; j++) {System.out.print(" ");}}private static void createRow(int[] row,int i){if (i == 0){row[0] = 1;return;}for (int j = i; j > 0 ; j--) {row[j] = row[j]+row[j-1];}}public static void Print(int n){int[] row = new int[n];for (int i = 0; i < n; i++) {createRow(row, i);printSpace(n,i);for (int j = 0; j <= i; j++) {// 格式化输出 宽度为4 从左对齐System.out.printf("%-4d",row[j]);}System.out.println();}}public static void main(String[] args) {Print(7);}
}

递归避免爆栈问题 —— 用循环代替递归
- 循环的空间复杂度通常较低,主要取决于循环体内声明的局部变量和使用的数据结构。
- 递归的空间复杂度较高,主要由递归调用的最大深度和每次递归所需的辅助空间决定。在设计和分析递归算法时,需要特别注意空间复杂度的控制,以避免栈溢出等问题。
五、递归时间复杂度的计算
其中,
① T(n)是问题的运行时间,n是数据规模
② a是子问题个数
③ T(n/b)是子问题运行时间,每个子问题被拆成原问题数据规模的n/b
④ f(n)是除递归外执行的计算
令x = logba,即 x = log子问题缩小倍数 子问题个数
则

1.公式求解
例一

例二

例三

例四

例五

二分查找递归
private static int Finding(int[] arr, int key,int i,int j) {if (i > j){return -1;}int m = (i + j) >>> 1;if (key == arr[m]) {return m;}else if (key < arr[m]) {j = m-1;return Finding(arr,key,i,j);}else {i = m+1;return Finding(arr,key,i,j);}}子问题个数:a = 1
子问题数据规模缩小倍数:b = 2
除递归外执行的计算是常数级 c = 0
T(n) = T(n/2) + n^b
此时 x = c = 0,时间复杂度是T(n^0*logn) = T(logn)
归并排序
// 归并排序private void split(int arr[],int i,int j,int arr2[]) {if(j-i <= 1){return;}int m = (i+j)/2;// 递归split(arr,i,m,arr2);split(arr,m,j,arr2);// 合并merge(arr,i,m,j,arr2);}子问题个数 a = 2
子问题数据规模缩小倍数 b = 2
除递归外,主要时间花在合并上,它可以用f(n) = n表示
T(n) = 2T(n/2) + n
此时 x = c = 1,时间复杂度是Θ(nlogn)
快速排序递归
// 快速排序递归private static void algorithm quicksort(int[] arr,int low,int high){if (low >= high || low < 0 || high >= arr.length){return;}// 分区int p = partition(arr,low,high);// 递归quicksort(arr,low,p-1);quicksort(arr,p+1,high);}子问题个数a = 2
子问题数据规模缩小倍数
如果分区分的好,b = 2
如果分区没分好,例如分区1的数据是0,分区2的数据是n-1除递归外,主要时间花在分区上,它可以用f(n) = n表示
情况1
分区分的好 T(n)=2T(n/2)+n
· 此时x=c=1,时间复杂度Θ(nlogn)
情况2分区没分好 T(n)=T(n-1)+T(1)+n
不成比例,此时不能用主定理求解
2.展开求解
递归式不能用公式求解,每次递归时间复杂度不同,所以将式子展开,求出每次递归的时间复杂度,进行累计求出最后的时间复杂度
例一 递归求和

例二 递归冒泡排序

例三 递归快排

相关文章:

数据结构与算法——Java实现 6.递归
要学会试着安静下来 —— 24.9.17 一、递归的定义 计算机科学中,递归是一种解决计算问题的方法,其中解决方案取决于同一类问题的更小子集 说明: ① 自己调用自己,如果说每个函数对应着一种解决方案,自己调用自己意味着解决方案是…...

.Net Core 生成管理员权限的应用程序
创建一个ASP.NET Core Web API项目 给解决方案设置一个名称 选择一个目标框架,这里选择的是 .NET 8.0框架 在Porperties文件夹中添加一个app.manifest文件 设置app.manifest文件属性,生成操作设置为嵌入的资源 双击解决方案名称,编辑WebAppli…...

DAY15:链表实现学生信息管理系统
要求功能: 创建学生信息表 头插法输入学生信息 尾插法输入学生信息输出任意位置范围内的学生信息 头删法删除学生信息尾删法删除学生信息按位置添加学生信息按位置删除学生信息 按位置修改学生信息按位置查找学生信息释放空间 今天有点累,懒得写注释了&a…...

JAVA语法基础 day05-面向对象
一、面向对象基本概念 /* 面向对象编程的步骤: 1.先设计对象的模板,也就是一个类class 生成一个新类的语句是:public class 类名,就跟python中class 类名一样 2.通过new关键字生成具体的对象,每new一次代表创建了的一个新的对象*…...

关于RabbitMQ重复消费的解决方案
一、产生原因 RabbitMQ在多种情况下可能会出现消息的重复消费。这些情况主要包括以下几个方面: 1. 网络问题 网络波动或中断:在消息处理过程中,由于网络波动或中断,消费者向RabbitMQ返回的确认消息(ack)…...

【SSM-Day2】第一个SpringBoot项目
运行本篇中的代码:idea专业版或者idea社区版本(2021.1~2022.1.4)->这个版本主要是匹配插件spring boot Helper的免费版(衰) 【SSM-Day2】第一个SpringBoot项目 框架->Spring家族框架快速上手Spring BootSpring Boot的作用通过idea创建S…...

【PyTorch】张量操作与线性回归
张量的操作 Tensor Operation 拼接与切分 1.1 torch.cat() torch.cat(tensors, dim0, outNone)功能:将张量按维度dim进行拼接 tensors:张量序列dim:要拼接的维度 1.2 torch.stacok() torch.stack(tensors, dim0, outNone)功能…...
情感类智能体——你的微信女神
智能体名称:你的微信女神 链接:文心智能体平台AgentBuilder | 想象即现实 (baidu.com)https://agents.baidu.com/agent/preview/RulbsUjIGj4wsinydlBH7AR3NQKFungt 简介 “你的微信女神”是一个直率的智能体,她用犀利而真实的言辞帮助用户…...

基于SpringBoot+Vue+MySQL的养老院管理系统
系统展示 管理员界面 家属界面 系统背景 随着全球人口老龄化的加速,养老院管理面临着前所未有的挑战。传统管理方式存在信息不透明、效率低下、资源分配不均等问题,难以满足日益增长的养老服务需求。因此,开发一套智能化、高效的养老院管理系…...

大数据Flink(一百二十二):阿里云Flink MySQL连接器介绍
文章目录 阿里云Flink MySQL连接器介绍 一、特色功能 二、语法结构 三、WITH参数 阿里云Flink MySQL连接器介绍 阿里云提供了MySQL连接器,其作为源表时,扮演的就是flink cdc的角色。 一、特色功能 MySQ…...

FutureTask源码分析
Thread类的run方法返回值类型是void,因此我们无法直接通过Thread类获取线程执行结果。如果要获取线程执行结果就需要使用FutureTask。用法如下: class CallableImpl implements Callable{Overridepublic Object call() throws Exception {//do somethin…...

Highcharts甘特图基本用法(highcharts-gantt.js)
参考官方文档: https://www.highcharts.com/docs/gantt/getting-started-gantt https://www.highcharts.com/demo/gantt/project-management https://www.hcharts.cn/demo/gantt 链接在下面按需引入 https://code.highcharts.com/gantt/highcharts-gantt.js htt…...

【Linux庖丁解牛】—Linux基本指令(上)!
🌈个人主页:秋风起,再归来~🔥系列专栏: Linux庖丁解牛 🔖克心守己,律己则安 目录 1、 pwd命令 2、ls 指令 3、cd 指令 4、Linux下的根目录 5、touch指令 6、 stat指令 7、mkdi…...
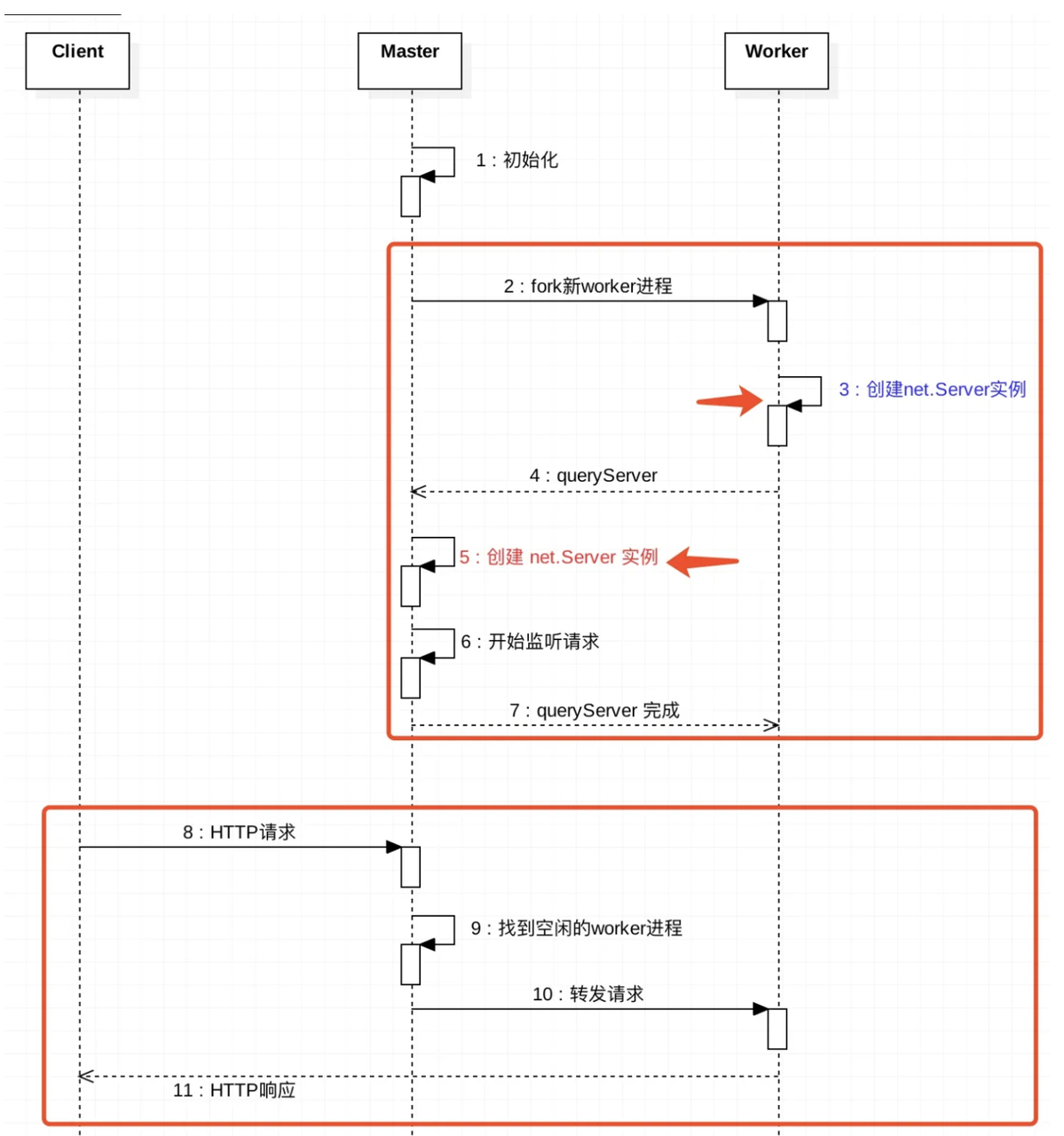
node.js 中的进程和线程工作原理
本文所有的代码均基于 node.js 14 LTS 版本分析 概念 进程是对正在运行中的程序的一个抽象,是系统进行资源分配和调度的基本单位,操作系统的其他所有内容都是围绕着进程展开的 线程是操作系统能够进行运算调度的最小单位,其是进程中的一个执…...

Qt/C++ TCP调试助手V1.1 新增图像传输与接收功能(附发布版下载链接)
发布版本链接 通过百度网盘分享的文件:TCP调试助手V1.zip(含客户端与服务器) 链接:https://pan.baidu.com/s/14LTRPChPhYdwp_s6KeyBiA?pwdcedu 提取码:cedu 基于Qt/C实现了一款功能丰富的TCP服务器与客户端调试助手…...

DNS解析流程
DNS解析流程: 浏览器DNS缓存: 当我们在浏览器中访问某个域名时,浏览器首先会检查自己内部的DNS缓存,看是否有该域名的对应IP地址。如果有,直接使用缓存中的IP地址,跳过后续步骤。 本地系统DNS缓存…...

[PTA]7-1 藏头诗
[PTA]7-1 藏头诗 本题要求编写一个解密藏头诗的程序。 注:在 2022 年 7 月 14 日 16 点 50 分以后,该题数据修改为 UTF-8 编码。 输入格式: 输入为一首中文藏头诗,一共四句,每句一行。注意:一个汉字占三…...

每日OJ题_牛客_WY22 Fibonacci数列(斐波那契)
目录 牛客_WY22 Fibonacci数列(斐波那契) 解析代码 牛客_WY22 Fibonacci数列(斐波那契) Fibonacci数列_牛客题霸_牛客网 解析代码 求斐波那契数列的过程中,判断⼀下:何时 n 会在两个 fib 数之间。 #in…...

SQL 查询语句汇总
在软件开发和数据分析中,SQL(结构化查询语言)是与数据库交互的重要工具。为了更好地理解 SQL 查询语句的使用,本文将设计一个简单的数据库,包括几张表,并通过这些表展示各种 SQL 查询的应用。 一、背景信息…...

封装一个语言识别文字的方法
语音识别 需求: 参考官方文档,整合语音识别apicallback 的写法改为 Promise 的版本 在startRecord中: 参考文档实例化-开启转换将录制的内容传递给录音识别回调函数中的 Log,改为 Logger 在closeRecord: 结束识别…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...
