LeetCode_单周赛_332
6354. 找出数组的串联值
题意
将数组首尾元素接在一起,就是串联值。
串联之后删除,如果只剩下一个元素,加上这个元素即可
双指针,从首和尾向中间移动即可
code
**注意:**用 long
没看题目用了 int wa了一发
class Solution {public long findTheArrayConcVal(int[] nums) {int n = nums.length;int l = 0, r = n - 1;long ans = 0;while (l < r) {String s = "";s += nums[l++];s += nums[r--];ans += Integer.parseInt(s);}if (l == r) ans += nums[l];return ans;}
}
6355. 统计公平数对的数目
题意
给定 lower 和 upper 找到 数组中 两个不同的数字,如果满足 lower <= nums[i] + nums[j] <= upper 就是一组公平数对。
求公平数对的个数
我们枚举每个 nums[i] 将 lower <= nums[i] + nums[j] <= upper 变形为:lower - nums[i] <= nums[j] <= upper - nums[i]
所以我们二分找到 第一个大于 upper - nums[i] 的位置,和 第一个 大于等于 lower- nums[i] 的位置前者减去后者即可得到差。
对应的 c++中的函数就是 uppper_bound 和 lower_bound,Java中么有这俩函数,我们自己写一个
并且,我们求的是数对,有重复的,为防止重复,我们只搜索下标为 i 的数的 左边的数,也避免了 i 被统计进去的情况
code
class Solution {public long countFairPairs(int[] nums, int lower, int upper) {long ans = 0;int n = nums.length;Arrays.sort(nums);// lower <= nums[i] + nums[j] <= upper// 枚举 nums[i] 找 j// lower - nums[i] <= nums[j] <= upper - nums[i]for (int i = 0; i < n; i++) { int a = i, b = i;// upper_boundint l = 0, r = i - 1;while (l < r) {int mid = l + r >> 1;if (nums[mid] > upper - nums[i]) r = mid;else l = mid + 1;}if (nums[l] > upper - nums[i]) a = l;// a = l;// if (nums[a] <= upper - nums[i]) a = i;// lower_boundl = 0; r = i - 1;while (l < r) {int mid = l + r >> 1;if (nums[mid] >= lower - nums[i]) r = mid;else l = mid + 1;}if (nums[l] >= lower - nums[i]) b = l;// b = l;// if (nums[b] < lower - nums[i]) b = i;ans += a - b;}return ans;}}
6356. 子字符串异或查询
题意
要满足 val ^ firsti == secondi 等号两边同时 ^ first 得到 val = first ^ second
所以我们只要找 queries数组中的 first 和 second 异或值时候存在于 s 中
因为 异或并不会增加二进制位数,0 <= firsti, secondi <= 109,小于 2^30 - 1,最多就 31 位,所以枚举的时候只需要枚举字符串的连续 30 个即可
s 是 1e4 时间复杂度最多就 1e4 * 30 = 3e5 足够的
后面枚举queries是 1e5
时间复杂度 = 4e5
用 map 预处理,存储 s 的二进制子串出现过的 十进制数字,以及对应的 边界 ,要求存储长度最小的子串
code
class Solution {public int[][] substringXorQueries(String s, int[][] queries) {HashMap<Integer, int[]> mp = new HashMap<>();int n = s.length();char[] c = s.toCharArray();for (int i = 0; i < n; i++) {int x = 0;for (int j = i; j < i + 30 && j < n; j++) { // 计算子串x = (x << 1) | (c[j] - '0');if (!mp.containsKey(x) || (j - i < mp.get(x)[1] - mp.get(x)[0])) {mp.put(x, new int[]{i, j});}}}ArrayList<int[]> a = new ArrayList<>();for (var pr : queries) {int t = pr[0] ^ pr[1];if (mp.getOrDefault(t, null) != null)a.add(new int[]{mp.get(t)[0], mp.get(t)[1]});else a.add(new int[]{-1, -1});}int len = a.size();int[][] ans = new int[len][2];for (int i = 0; i < len; i++) {ans[i] = a.get(i);}return ans;}}
相关文章:

LeetCode_单周赛_332
6354. 找出数组的串联值 题意 将数组首尾元素接在一起,就是串联值。 串联之后删除,如果只剩下一个元素,加上这个元素即可 双指针,从首和尾向中间移动即可 code **注意:**用 long 没看题目用了 int wa了一发 clas…...
[LeetCode周赛复盘] 第 332 场周赛20230212
[LeetCode周赛复盘] 第 332 场周赛20230212 一、本周周赛总结二、 [Easy] 6354. 找出数组的串联值1. 题目描述2. 思路分析3. 代码实现三、[Medium] 6355. 统计公平数对的数目1. 题目描述2. 思路分析3. 代码实现四、[Medium] 6356. 子字符串异或查询1. 题目描述2. 思路分析3. 代…...

C++轻量级RPC库RpcCore
C轻量级的RPC库,可用于任何项目中,甚至单片机。 方便平台直接相互进行功能调用。 基于asio的实现 asio_net 也可用在esp32适用于ESP32/ESP8266的实现 esp_rpc 目前也有一些轻量的库,参考了protobuf(或者依赖它)&…...

Mysql的视图
视图的特点: 1.视图可以看做一个虚拟的表,本身是不存储数据的。 视图的本质可以看作是存储起来的select语句 2.视图中涉及到的表都统称为基表 3.针对视图多DML操作,会影响到对应基表中的数据。反之亦然 4.视图本身的删除,不会…...

2/12考试总结
时间安排 8:30–8:50 读题,T1 不知道是个啥,T2是个dp ,T3可能也是 dp 之类的。 8:50–9:30 T1,读了好几遍才理解了题意,对于部分分有爆搜。考虑正解,想到预处理后O(1) 查询,问题是如何由已知的信息得到所有…...
第三章虚拟机的克隆,快照,迁移删除
1.虚拟机的克隆 如果你已经安装了一台linux操作系统,你还想再更多的,没有必要再重新安装,你只需要克 隆就可以,看演示。 方式1,直接拷贝一份安装好的虚拟机文件,再用虚拟机打开这个文件方式2,使用vmware的…...
| 真题含思路)
华为OD机试 - 任务总执行时长(Python)| 真题含思路
任务总执行时长 题目 任务编排服务负责对任务进行组合调度。 参与编排的任务又两种类型, 其中一种执行时长为taskA, 另一种执行时长为taskB。 任务一旦开始执行不能被打断,且任务可连续执行。 服务每次可以编排 num 个任务。 请编写一个方法,生成每次编排后的任务所有可…...
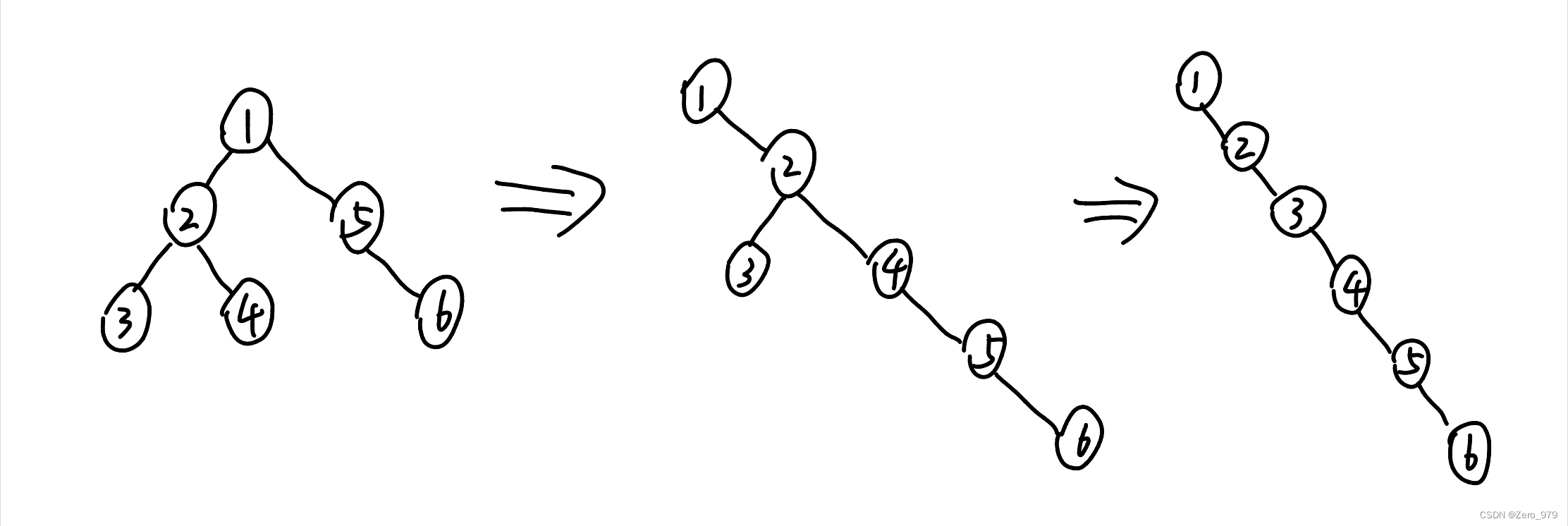
LeetCode 热题 C++ 114. 二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表: 展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。展开后的单链表应该与二叉树 先序遍历 顺序相同。 示例 1…...

Spring的事务控制-基于AOP的声明式事务控制
Spring的事务控制-基于AOP的声明式事务控制 Spring事务编程概述 事务是开发中必不可少的东西,使用JDBC开发时,我们使用connection对事务进行控制,使用MyBatis时,我们使用SqlSession对事务进行控制,缺点就是ÿ…...
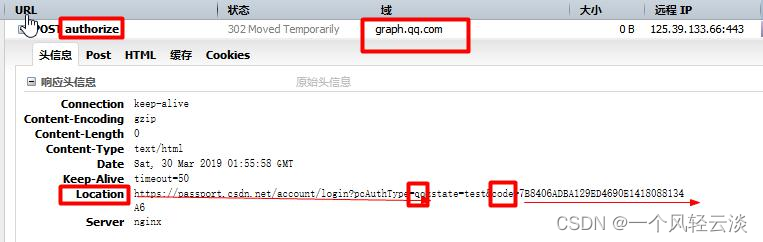
SSO(单点登陆)
Single Sign On 一处登陆、处处可用 0、前置概念: 1)、单点登录业务介绍 早期单一服务器,用户认证。 缺点:单点性能压力,无法扩展 分布式, SSO(single sign on)模式 解决 : 用户身份信息独…...
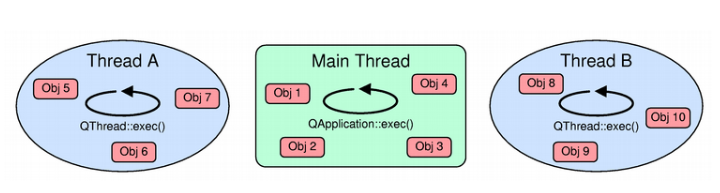
线程和QObjects
QObject的可重入性: QThread继承了QObject,它发出信号以指示线程开始或完成执行,并提供一些插槽。 QObjects可以在多个线程中使用发出调用其他线程中槽的信号,并将事件发布到在其他线程中“活动”的对象。这是可能的࿰…...

最新中文版FL Studio21水果软件下载安装图文教程
FL Studio是目前流行广泛使用人数最多音乐编曲制作软件,这款软件相信广大网友并不陌生,今天带来的是FL中文版本,所有的功能都能在线编辑,用户直接就能操作,同时因为是21水果是最新版,所以增加了新的功能&am…...

pandas数据分析35——多个数据框实现笛卡尔积
什么是笛卡尔积。就是遍历所有组合的可能性。 比如第一个盒子有[1,2,3]三个号码球,第二个盒子有[4,5]两个号码球。那么从每个盒子里面分别拿一个球共有3*2两种可能性,其集合就是{[1,4],[2,4],[3,4],[1,5],[2,5],[3,5]},这个就是笛卡尔积。 三个盒子也是…...

【C语言学习笔记】:数组倒序排列,数组倒置
数组倒置就是将数组元素中的数据倒过来! 举个例子,比如下面程序: #include <stdio.h>int main(void) { int a[5] {1, 2, 3, 4, 5}; int b[5]; //用来存放倒置后的数据 int i, j; for (i0, j4; i<5, j>0; i, --j)…...
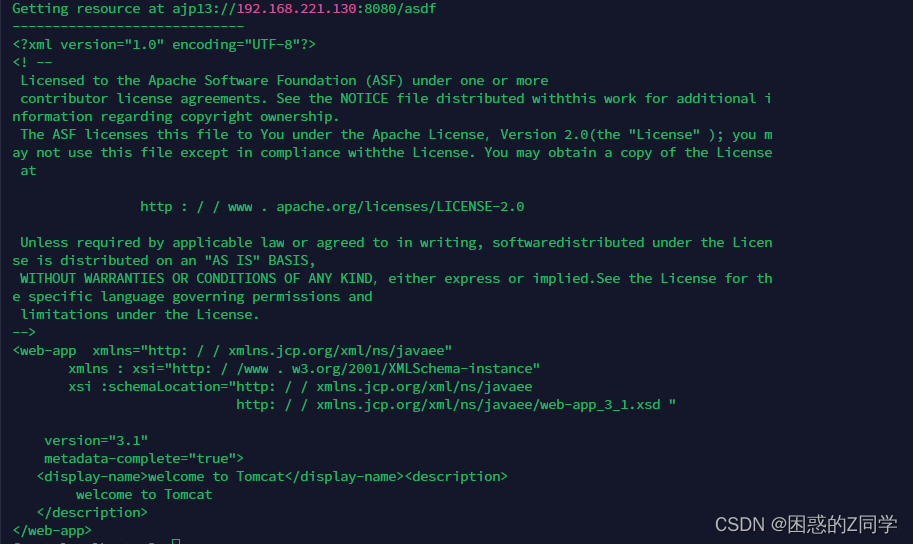
sni+tomcat漏洞复现
sni SNI产生背景 SSL以及TLS(SSL的升级版)为客户端与服务器端进行安全连接提供了条件。但是,由于当时技术限制,SSL初期的设计顺应经典的公钥基础设施 PKI(Public Key Infrastructure)设计,PKI 认为一个服务器只为一个…...
Linux ALSA 之十:ALSA ASOC Machine Driver
ALSA ASOC Machine Driver一、Machine 简介二、ASoC Machine Driver2.1 Machine Driver 的 Platform Driver & Platform Device 驱动模型2.2 在 Probe() 中注册声卡三、snd_soc_register_card 函数3.1 bind DAIs3.2 New a sound card3.3 Create card new widgets3.4 Probe …...

Spring 面试题(一):Spring 如何处理全局异常?
❤️ 博客首页:水滴技术 🚀 支持水滴:点赞👍 收藏⭐ 留言💬 🌸 订阅专栏:Spring 教程:从入门到精通 文章目录1、如何处理全局异常2、代码示例2.1、定义统一的“响应结果对象”2.2、…...
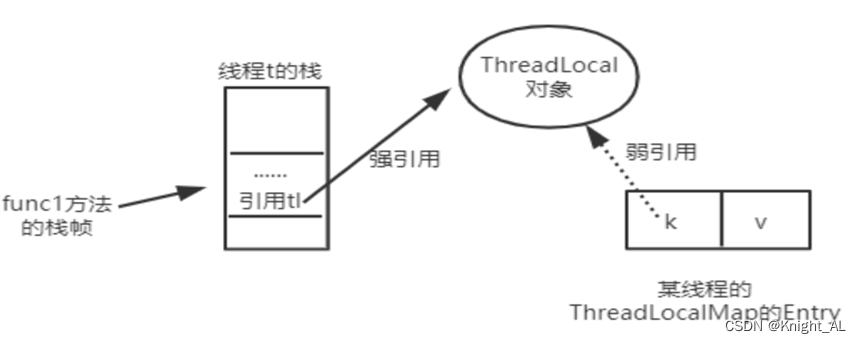
Threadlocal为何引发内存泄漏问题
首先我们要先了解什么是泄漏问题和什么是内存溢出 内存泄漏表示程序员申请了内存,但是该内存一直无法被释放 内存溢出表示申请内存不足,就会报错 为何引发内存泄漏问题 因为每个线程都有自己独立的ThreadLocalMap对象,key为ThreadLocal&…...

如何写好 Python 的 Lambda 函数?
当你需要完成一件小工作时,在本地环境中使用这个函数,可以让工作如此得心应手,它就是 Lambda 函数。 Lambda 函数是 Python 中的匿名函数。有些人将它们简称为lambdas,它们的语法如下: lambda arguments: expression…...

大数据技术架构(组件)32——Spark:Spark SQL--Execute Engine
2.2、Spark SQL2.2.1、Execute EngineSparkSql的整体提交执行流程和Hive的执行流程基本上一致。站在通用的角度,对于SparkSql来说,从Sql到Spark的RDD执行需要经历两个大的阶段:逻辑计划和物理计划逻辑计划层面会把用户提交的sql转换成树型结构…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
