从0开始学python -69
Python math 模块
Python math 模块提供了许多对浮点数的数学运算函数。
math 模块下的函数,返回值均为浮点数,除非另有明确说明。
如果你需要计算复数,请使用 cmath 模块中的同名函数。
要使用 math 函数必须先导入:
import math
查看 math 模块中的内容:
import mathdir(math)['__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atan2', 'atanh', 'ceil', 'comb', 'copysign', 'cos', 'cosh', 'degrees', 'dist', 'e', 'erf', 'erfc', 'exp', 'expm1', 'fabs', 'factorial', 'floor', 'fmod', 'frexp', 'fsum', 'gamma', 'gcd', 'hypot', 'inf', 'isclose', 'isfinite', 'isinf', 'isnan', 'isqrt', 'lcm', 'ldexp', 'lgamma', 'log', 'log10', 'log1p', 'log2', 'modf', 'nan', 'nextafter', 'perm', 'pi', 'pow', 'prod', 'radians', 'remainder', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'tau', 'trunc', 'ulp']
math 模块常量
| 常量 | 描述 |
|---|---|
| math.e | 返回欧拉数 (2.7182…) |
| math.inf | 返回正无穷大浮点数 |
| math.nan | 返回一个浮点值 NaN (not a number) |
| math.pi | π 一般指圆周率。 圆周率 PI (3.1415…) |
| math.tau | 数学常数 τ = 6.283185…,精确到可用精度。Tau 是一个圆周常数,等于 2π,圆的周长与半径之比。 |
math 模块方法
| 方法 | 描述 |
|---|---|
| math.acos(x) | 返回 x 的反余弦,结果范围在 0 到 pi 之间。 |
| math.acosh(x) | 返回 x 的反双曲余弦值。 |
| math.asin(x) | 返回 x 的反正弦值,结果范围在 -pi/2 到 pi/2 之间。 |
| math.asinh(x) | 返回 x 的反双曲正弦值。 |
| math.atan(x) | 返回 x 的反正切值,结果范围在 -pi/2 到 pi/2 之间。 |
| math.atan2(y, x) | 返回给定的 X 及 Y 坐标值的反正切值,结果是在 -pi 和 pi 之间。 |
| math.atanh(x) | 返回 x 的反双曲正切值。 |
| math.ceil(x) | 将 x 向上舍入到最接近的整数 |
| math.comb(n, k) | 返回不重复且无顺序地从 n 项中选择 k 项的方式总数。 |
| math.copysign(x, y) | 返回一个基于 x 的绝对值和 y 的符号的浮点数。 |
| math.cos() | 返回 x 弧度的余弦值。 |
| math.cosh(x) | 返回 x 的双曲余弦值。 |
| math.degrees(x) | 将角度 x 从弧度转换为度数。 |
| math.dist(p, q) | 返回 p 与 q 两点之间的欧几里得距离,以一个坐标序列(或可迭代对象)的形式给出。 两个点必须具有相同的维度。 |
| math.erf(x) | 返回一个数的误差函数 |
| math.erfc(x) | 返回 x 处的互补误差函数 |
| math.exp(x) | 返回 e 的 x 次幂,E x , 其中 e = 2.718281… 是自然对数的基数。 |
| math.expm1() | 返回 Ex - 1, e 的 x 次幂,E x ,其中 e = 2.718281… 是自然对数的基数。这通常比 math.e ** x 或 pow(math.e, x) 更精确。 |
| math.fabs(x) | 返回 x 的绝对值。 |
| math.factorial(x) | 返回 x 的阶乘。 如果 x 不是整数或为负数时则将引发 ValueError。 |
| math.floor() | 将数字向下舍入到最接近的整数 |
| math.fmod(x, y) | 返回 x/y 的余数 |
| math.frexp(x) | 以 (m, e) 对的形式返回 x 的尾数和指数。 m 是一个浮点数, e 是一个整数,正好是 x == m * 2**e 。 如果 x 为零,则返回 (0.0, 0) ,否则返回 0.5 <= abs(m) < 1 。 |
| math.fsum(iterable) | 返回可迭代对象 (元组, 数组, 列表, 等)中的元素总和,是浮点值。 |
| math.gamma(x) | 返回 x 处的伽马函数值。 |
| math.gcd() | 返回给定的整数参数的最大公约数。 |
| math.hypot() | 返回欧几里得范数,sqrt(sum(x**2 for x in coordinates))。 这是从原点到坐标给定点的向量长度。 |
| math.isclose(a,b) | 检查两个值是否彼此接近,若 a 和 b 的值比较接近则返回 True,否则返回 False。。 |
| math.isfinite(x) | 判断 x 是否有限,如果 x 既不是无穷大也不是 NaN,则返回 True ,否则返回 False 。 |
| math.isinf(x) | 判断 x 是否是无穷大,如果 x 是正或负无穷大,则返回 True ,否则返回 False 。 |
| math.isnan() | 判断数字是否为 NaN,如果 x 是 NaN(不是数字),则返回 True ,否则返回 False 。 |
| math.isqrt() | 将平方根数向下舍入到最接近的整数 |
| math.ldexp(x, i) | 返回 x * (2**i) 。 这基本上是函数 math.frexp() 的反函数。 |
| math.lgamma() | 返回伽玛函数在 x 绝对值的自然对数。 |
| math.log(x[, base]) | 使用一个参数,返回 x 的自然对数(底为 e )。 |
| math.log10(x) | 返回 x 底为 10 的对数。 |
| math.log1p(x) | 返回 1+x 的自然对数(以 e 为底)。 |
| math.log2(x) | 返回 x 以 2 为底的对数 |
| math.perm(n, k=None) | 返回不重复且有顺序地从 n 项中选择 k 项的方式总数。 |
| math.pow(x, y) | 将返回 x 的 y 次幂。 |
| math.prod(iterable) | 计算可迭代对象中所有元素的积。 |
| math.radians(x) | 将角度 x 从度数转换为弧度。 |
| math.remainder(x, y) | 返回 IEEE 754 风格的 x 除于 y 的余数。 |
| math.sin(x) | 返回 x 弧度的正弦值。 |
| math.sinh(x) | 返回 x 的双曲正弦值。 |
| math.sqrt(x) | 返回 x 的平方根。 |
| math.tan(x) | 返回 x 弧度的正切值。 |
| math.tanh(x) | 返回 x 的双曲正切值。 |
| math.trunc(x) | 返回 x 截断整数的部分,即返回整数部分,删除小数部分 |
相关文章:

从0开始学python -69
Python math 模块 Python math 模块提供了许多对浮点数的数学运算函数。 math 模块下的函数,返回值均为浮点数,除非另有明确说明。 如果你需要计算复数,请使用 cmath 模块中的同名函数。 要使用 math 函数必须先导入: import…...

HashMap中HashCode的实现原理
代码 static final int hash(Object key) {int h;return (key null) ? 0 : (h key.hashCode()) ^ (h >>> 16);}1. h >>> 16 是什么,有什么用? h是hashcode。h >>> 16是用来取出h的高16,(>>>是无符号右移) 如下展…...
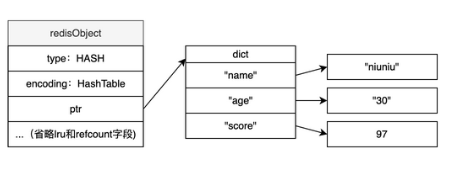
Redis —Set、ZSet介绍和应用场景
Set 概念 Redis的set是一个不重复、无序并唯一的键值集合。(方便管理无序集合)它支持交集、并集、差集等等 set和list区别 List 可以存储重复元素,Set 只能存储非重复元素;List 是按照元素的先后顺序存储元素的,而…...

【产品人卫朋】内容运营:文章点击量少的可怜,该怎么做?
今天来谈谈内容运营这个话题。 随着自媒体进入视播时代,也就是短视频的时代。 无论你打开任何一个短视频应用,每一个主题下面都会有成千上万个视频。 最为致命的是,大家停留的时间也越来越短了。 如果你不能在2秒的时间内吸引眼球,…...

【K8S系列】深入解析无状态服务
目录 序言 1. 无服务介绍 1.1 优点 1.2 使用场景 1.3 资源类型 1.4 总结 2 使用介绍 2.1 Deployment 使用场景: 2.2 ReplicaSet 使用场景 2.3 pod Pod 资源定义示例 2.4 service 创建一个Deployment: 创建一个Service: 总结…...

Node基础--命令窗口
1.Windows命令行窗口(叫做:小黑屏、cmd窗口、终端、shell) (1).如何打开命令行窗口 开始菜单 -- 运行 --- cmd --- enter win R -- cmd --- enter (2).cmd窗口常用指令 dir 列出当前目录下的所有文件 cd 目录名 进入到指定的目录 md 目录名 …...

一些有趣的项目
一个支持交互的展示卷积过程的可视化工具 https://github.com/pwwang/cnn-convoluter 一款简单易用基于 Python scikit 的推荐系统https://github.com/NicolasHug/Surprise 一个封装了 7 种启发式算法的 Python 代码库。分别是:差分进化算法、遗传算法、粒子群算法…...

教你精通JavaSE语法之第六章、数组的使用
一、数组的定义与使用 😁1.1数组的概念📌数组:可以看成是相同类型元素的一个集合。在内存中是一段连续的空间,可以同来存储同种数据类型的多个值。但是数组容器在存储数据的时候,需要结合隐式转换考虑。比如࿱…...
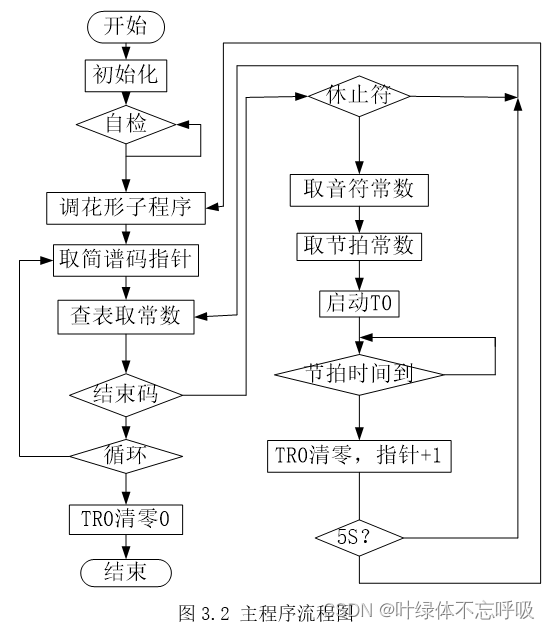
基于51单片机AT89C51的小型音乐喷泉控制系统设计
wx供重浩:创享日记 对话框发送:单片机小喷泉 获取完整无水印论文报告(内含电路原理图和程序) 根据目前音乐喷泉的发展现状,介绍了一个以AT89C51单片机为核心的小型音乐喷泉控制系统。给出了一个简洁的单片机控制电路&a…...
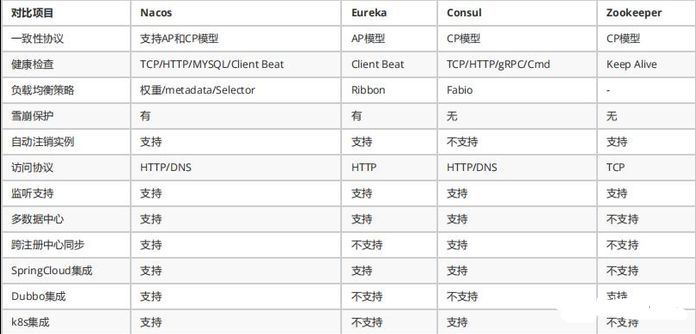
【Nacos】Nacos原理详解(注册中心,配置中心)
文章目录一、背景二、CAP理论三、什么是NacosNacos 服务注册需要具备的能力:Nacos的实现原理:四、Nacos原理Nacos 服务注册与订阅的完整流程服务领域模型五、注册中心原理六、配置中心原理七、Nacos 的关键特性包括:八、 面试分析一、背景 服务注册中心…...

蓝桥杯刷题冲刺 | 倒计时11天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.质因子2.蓝桥王国1.质因子 题目 链接: 1545. 质因子 - AcWing题库 给定一个整数 N…...

【新】(2023Q2模拟题JAVA)华为OD机试 - 时间格式化
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:时间格式化 题目 运维工程师…...
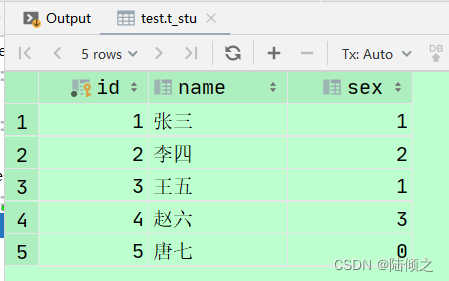
MySQL函数
函数 MySQL函数与其存储过程类似,是一系列完成某种功能的SQL语句。函数一旦定义后,与过程一样是存储在MySQL的服务器上。调用函数就是一次性执行这些语句。所以函数可以降低语句重复。 MySQL本身提供了内置函数,这些函数的存在给我们日常的开…...

【Linux系统】开发工具(下) {调试器gdb,自动化构建工具make/Makefile,多文件编译,代码管理平台git}
【Linux系统】开发工具(上) {软件包管理器yum,更新yum源,文本编辑器vim,vim的三种基本模式,vim指令集,代码编译器gcc/g} 四、Linux调试器:gdb 4.1 debug模式 程序的编译模式有两种,debug模式和…...

线性代数——行列式
文章目录版权声明排列行列式行列式的由来行列式的概念行列式的性质重要公式克拉默法则补充知识版权声明 本文大部分内容皆来自李永乐老师考研教材和视频课。 排列 由1,2,…,n1,2,\ldots,n1,2,…,n组成的有序数组称为一个nnn阶排列,通常使用j1j2…jnj_1j_2\ldots …...

Spring注解-Spring-boot-SpingAOP
Spring各个模块 Test 对应spring-test.jar. Spring提供的测试工具, 可以整合JUnit测试, 简化测试环节. Core Container Spring的核心组件, 包含了Spring框架最基本的支撑. Beans, 对应spring-beans.jar. Spring进行对象管理时依赖的jar包. Core, 对应spring-core.jar,…...

使用Shell传参解决DataPhin中PySpark不支持中文的问题
使用Shell传参解决DataPhin中PySpark不支持中文的问题 背景 笔者开发PySpark任务时【别问为神马不用Java和Scala打Jar包的方式,PySpark不需要打包所以开发效率极高,早点搞完早点下班】,遇到一个令所有SQL Boy都很头疼的问题,那就…...
【CDH】cloudera manger 如何开启Debug 日志调试模式
前言 在安装 Cloudera Manger 时,遇到报错,需要开启Debug 日志级别来排查下问题原因。这里记录下 CM 如何开启 Debug 级别。 方法一:为整个服务启动DEBUG 如果 CM 无法启动,则可以为整个服务器启用 DEBUG 或 TRACE。 警告&…...

SQL Server 用户授权与回收
创建xxbbbb账号,账号可以在Company_report20221019.dbo.qfacccmprf表中进行select、 insert,update,delete --创建登录账号 create login xxbbbb with password12345#---创建用户 use Company_report20221019 create user xxbbbb for login xxbbbb---将qfacccmprf表…...

电脑出现乱码的原因以及解决方法
在日常使用电脑的过程中,经常会遇到电脑出现乱码,那么为什么会出现乱码呢?出现乱码又该怎么解决呢?下面我们一起来了解一下。 出现乱码的原因 系统乱码:主要是Windows中显示乱码,比如菜单、桌面、启动界面…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
