BFS 解决多源最短路问题
文章目录
- 多源BFS
- 542. 01 矩阵
- 题目解析
- 算法原理
- 代码实现
- 1020. 飞地的数量
- 题目解析
- 算法原理
- 1765. 地图中的最高点
- 题目解析
- 算法原理
- 代码实现
- 1162. 地图分析
- 题目解析
- 算法原理
- 代码实现
多源BFS
单源最短路: 一个起点、一个终点
多源最短路: 可以多个起点,一个终点
多源BFS: 用BFS解决边权为1的多源最短路(😂)
BFS 解决边权为1的最短路问题
如何解决:
- 解法一:暴力枚举,把多源最短路转换成若干个单源最短路(大概率超时)
- 解法二:把所有源点当成一个“超级源点”,问题就变成了单一的单源最短路问题
想办法将若干个起点,当作一个起点
为什么正确? 如图:
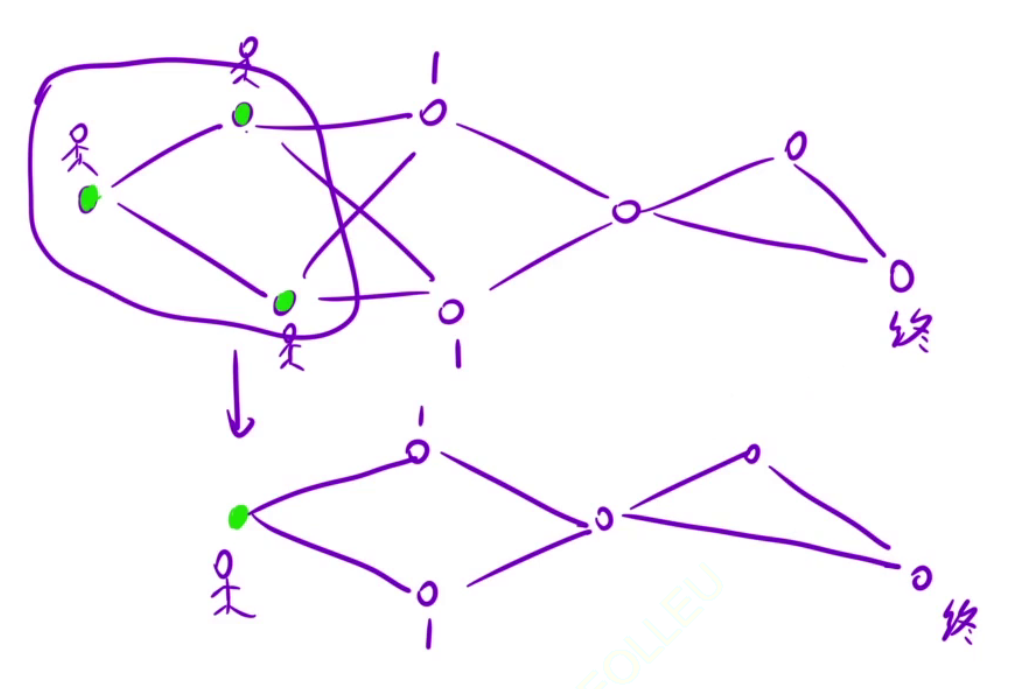
如何代码实现:
- 所有起点加入到队列当中
- 一层一层向外扩展
542. 01 矩阵
题目链接:542. 01 矩阵
题目解析
给我们一个矩阵,矩阵由0和1组成
要我们返回的也是一个矩阵,里面放的是每个位置里0最近的距离
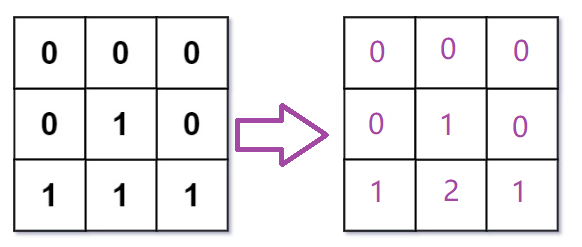
算法原理
- 把所有的0当成起点,1当成终点
- 将所有
0位置加入队列 - 一层一层向外扩展
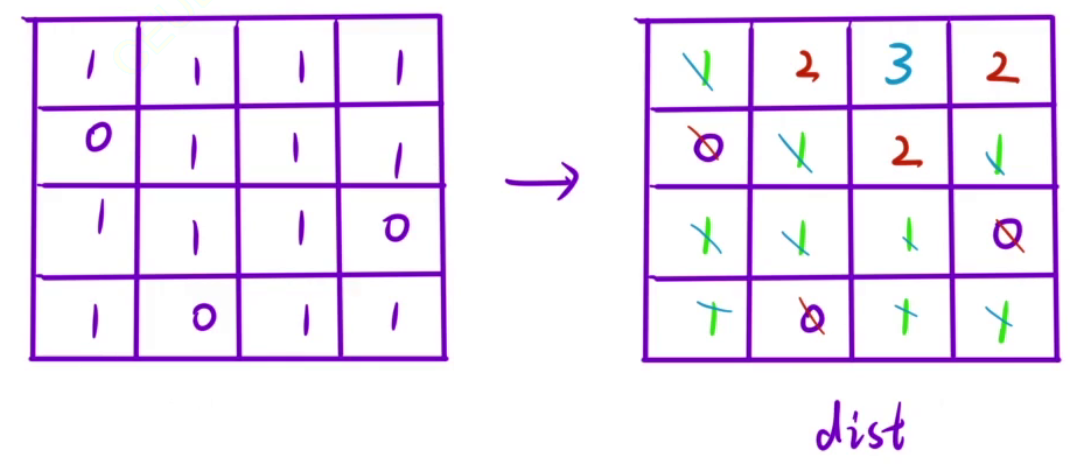
代码实现
class Solution {
public:int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};vector<vector<int>> updateMatrix(vector<vector<int>>& mat){int m = mat.size();int n = mat[0].size();vector<vector<int>> dist(m, vector<int>(n, -1));queue<pair<int, int>> q;for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){if(mat[i][j] == 0){q.push({i, j});dist[i][j] = 0;}}}while(q.size()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; k++){int x = dx[k] + a;int y = dy[k] + b;if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1){dist[x][y] = dist[a][b] + 1;q.push({x, y});}}}return dist;}
};
1020. 飞地的数量
题目链接:1020. 飞地的数量
题目解析
给我们一个矩阵,由0和1组成,1表示陆地,0表示海洋
要我们求出,无法“上岸”数量
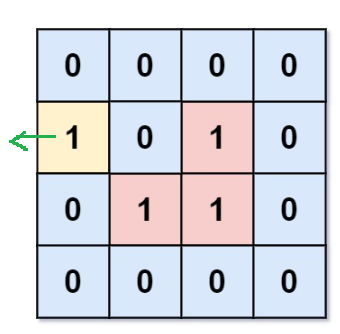
算法原理
正难则反:
直接看四个边界,是否有“陆地”
如果有,直接往里面搜索,看有多少连在一起的
class Solution {
public:int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int numEnclaves(vector<vector<int>>& grid){int m = grid.size();int n = grid[0].size();vector<vector<bool>> vis(m, vector<bool>(n));queue<pair<int, int>> q;//四周 1 加入队列for(int j = 0; j < n; j++){if(grid[0][j] == 1) {q.push({0, j});vis[0][j] = true;}if(grid[m-1][j] == 1){q.push({m-1, j});vis[m-1][j] = true;} }for(int i = 0; i < m; i++){if(grid[i][0] == 1){q.push({i, 0});vis[i][0] = true;}if(grid[i][n - 1] == 1){q.push({i, n-1});vis[i][n-1] = true;}}//多源bfswhile(q.size()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; k++){int x = dx[k] + a;int y = dy[k] + b;if(x >= 0 && y >= 0 && x < m && y < n && grid[x][y] == 1 && !vis[x][y]){vis[x][y] = true;q.push({x, y});}}}int ret = 0;for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){if(grid[i][j] == 1 && !vis[i][j]) ret++;}}return ret;}
};
1765. 地图中的最高点
题目链接:1765. 地图中的最高点
题目解析
给我们一个矩阵,由陆地和水域组成
isWater[i][j] == 0为陆地isWater[i][j] == 1为水域
规则如下:
- 格子高度非负
- 格子为水域,高度为0
- 相邻格子,高度差不大于1
最终要得出,怎么排列,能得到让最高的高度最大。
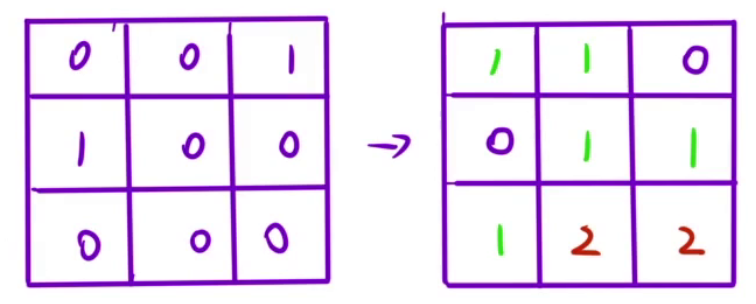
算法原理
- 这里最先排列的肯定是水域,如果是水域,设置为
0,即先遍历矩阵,将水域格子加入队列 - 然后一层一层向外扩展
代码实现
class Solution {
public:int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};vector<vector<int>> highestPeak(vector<vector<int>>& isWater){int m = isWater.size();int n = isWater[0].size();vector<vector<int>> dist(m,vector<int>(n, -1));queue<pair<int, int>> q;for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){if(isWater[i][j] == 1){dist[i][j] = 0;q.push({i, j});}}}while(q.size()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; k++){int x = dx[k] + a;int y = dy[k] + b;if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1){dist[x][y] = dist[a][b] + 1;q.push({x, y});}}}return dist;}
};
1162. 地图分析
题目链接:1162. 地图分析
题目解析
给我一个矩阵,0和1组成
0表示海洋1表示陆地
要我们找出海洋离陆地的最大距离(曼哈顿距离, a+b)
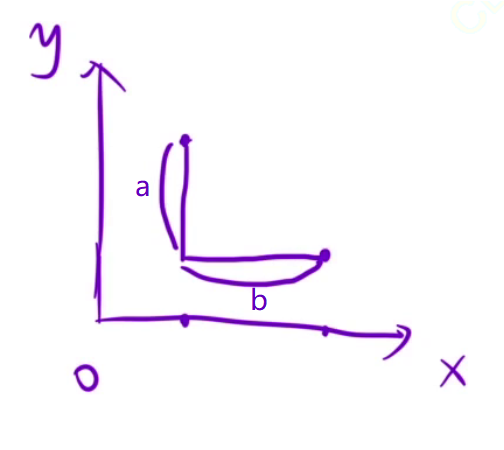
算法原理
反过来,陆地到海洋的距离,一层一层往外扩
- 陆地加入队列,此时距离为1
- 往外扩展
代码实现
class Solution {
public:int dx[4] = {0, 0, -1, 1};int dy[4] = {1, -1, 0 ,0};int maxDistance(vector<vector<int>>& grid){int m = grid.size();int n = grid[0].size();vector<vector<int>> dist(m, vector<int>(n, -1));queue<pair<int, int>> q;for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){if(grid[i][j] == 1){dist[i][j] = 0;q.push({i, j});}}}int ret = -1;while(q.size()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; k++){int x = dx[k] + a;int y = dy[k] + b;if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1){dist[x][y] = dist[a][b] + 1;q.push({x, y});ret = dist[x][y];}} }return ret;}
};
相关文章:

BFS 解决多源最短路问题
文章目录 多源BFS542. 01 矩阵题目解析算法原理代码实现 1020. 飞地的数量题目解析算法原理 1765. 地图中的最高点题目解析算法原理代码实现 1162. 地图分析题目解析算法原理代码实现 多源BFS 单源最短路: 一个起点、一个终点 多源最短路: 可以多个起点…...

论文笔记:交替单模态适应的多模态表征学习
整理了CVPR2024 Multimodal Representation Learning by Alternating Unimodal Adaptation)论文的阅读笔记 背景MLA框架实验Q1 与之前的方法相比,MLA能否克服模态懒惰并提高多模态学习性能?Q2 MLA在面临模式缺失的挑战时表现如何?Q3 所有模块是否可以有…...

鸿蒙OS 线程间通信
鸿蒙OS 线程间通信概述 在开发过程中,开发者经常需要在当前线程中处理下载任务等较为耗时的操作,但是又不希望当前的线程受到阻塞。此时,就可以使用 EventHandler 机制。EventHandler 是 HarmonyOS 用于处理线程间通信的一种机制,…...

执行 npm报错 Cannot find module ‘../lib/cli.js‘
报错 /usr/local/node/node-v18.20.4-linux-x64/bin/npm node:internal/modules/cjs/loader:1143 throw err; ^ Error: Cannot find module ../lib/cli.js Require stack: - /usr/local/node/node-v18.20.4-linux-x64/bin/npm at Module._resolveFilename (node:inter…...

基于SpringBoot+Vue+MySQL的国产动漫网站
系统展示 用户前台界面 管理员后台界面 系统背景 随着国内动漫产业的蓬勃发展和互联网技术的快速进步,动漫爱好者们对高质量、个性化的国产动漫内容需求日益增长。然而,市场上现有的动漫平台大多以国外动漫为主,对国产动漫的推广和展示存在不…...

AUTOSAR汽车电子嵌入式编程精讲300篇-基于CAN总线的气动控制
目录 前言 知识储备 什么是气动控制: 气动控制基础知识 一、气动元件 二、气路设计 三、气动控制系统 气动控制系统构成图 气动控制系统基本组成功能图 几种常见的气动执行元件实物图 常用气动压力控制阀实物图 常用气动流动控制阀实物图 电磁控制换向发实物图 部…...

Ubuntu 20.04 内核升级后网络丢失问题的解决过程
在 Ubuntu 系统中,内核升级是一个常见的操作,旨在提升系统性能、安全性和兼容性。然而,有时这一操作可能会带来一些意外的副作用,比如导致网络功能的丧失。 本人本来是想更新 Nvidia 显卡的驱动,使用 ubuntu-drivers …...

论文解读《LaMP: When Large Language Models Meet Personalization》
引言:因为导师喊我围绕 “大语言模型的个性化、风格化生成” 展开研究,所以我就找相关论文,最后通过 ACL 官网找到这篇,感觉还不错,就开始解读吧! “说是解读,其实大部分都是翻译哈哈哈&#x…...
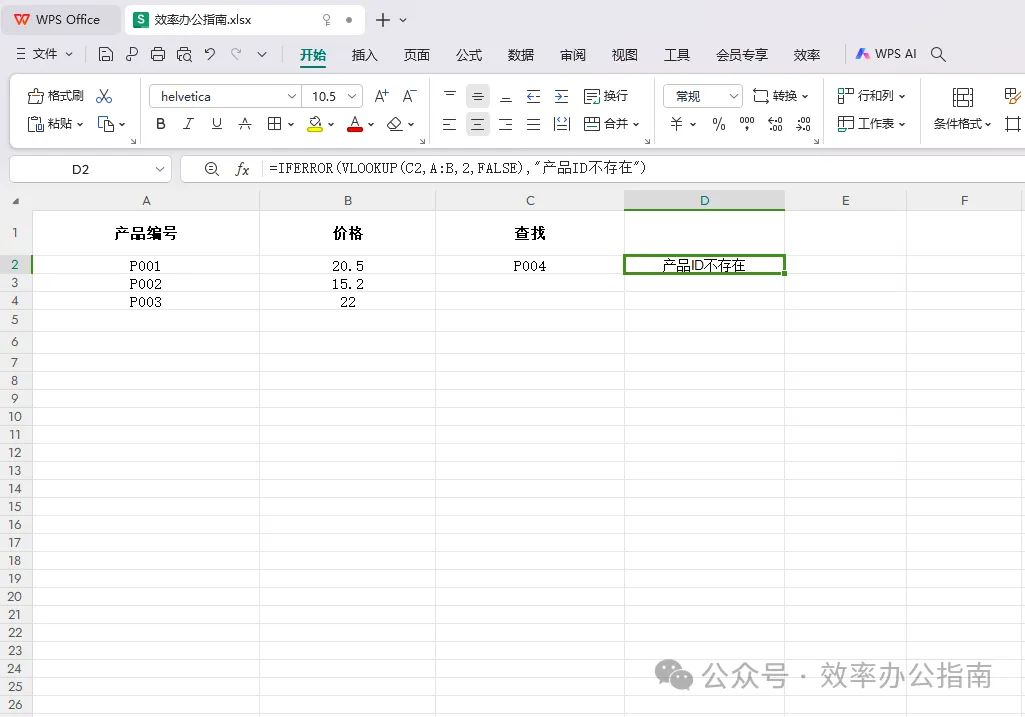
Excel VLOOKUP函数怎么用?vlookup函数的使用方法及案例
大家好,这里是效率办公指南! 🔎 在Excel的世界里,VLOOKUP函数无疑是查询和数据分析中的明星。无论是从庞大的数据表中提取特定信息,还是进行数据的快速匹配,VLOOKUP都能大显身手。今天,我们将深…...

专为汽车功能应用打造的 MLX90376GGO、MLX90377GGO、MLX90377GDC-ADB-280 Triaxis®磁位置传感器 IC
一、MLX90376 Triaxis堆叠式高性能位置传感器芯片(模拟/PWM/SENT/SPC) MLX90376GGO-ABA-600 MLX90376GGO-ABA-630 MLX90376GGO-ABA-680 MLX90376是一款磁性绝对位置传感器芯片,适用于要求具备抗杂散磁场干扰性能的360旋转汽车应用。它提供…...

34.贪心算法1
0.贪心算法 1.柠檬水找零(easy) . - 力扣(LeetCode) 题目解析 算法原理 代码 class Solution {public boolean lemonadeChange(int[] bills) {int five 0, ten 0;for (int x : bills) {if (x 5) // 5 元:直接收下…...

DataX实战:从MongoDB到MySQL的数据迁移--修改源码并测试打包
在现代数据驱动的业务环境中,数据迁移和集成是常见的需求。DataX,作为阿里云开源的数据集成工具,提供了强大的数据同步能力,支持多种数据源和目标端。本文将介绍如何使用DataX将数据从MongoDB迁移到MySQL。 环境准备 安装MongoDB…...

Axure设计之表格列冻结(动态面板+中继器)
在Web端产品设计中,复杂的表格展示是常见需求,尤其当表格包含大量列时,如何在有限的屏幕空间内优雅地展示所有信息成为了一个挑战。用户通常需要滚动查看隐藏列,但关键信息列(如ID、操作按钮等)在滚动时保持…...

WPF DataGrid 动态修改某一个单元格的样式
WPF DataGrid 动态修改某一个单元格的样式 <DataGrid Name"main_datagrid_display" Width"1267" Height"193" Grid.Column"1"ItemsSource"{Binding DataGridModels}"><DataGrid.Columns><!--ElementStyle 设…...

如何安装部署kafka
安装和部署Apache Kafka需要以下几个步骤,包括下载 Kafka、配置 ZooKeeper(或者使用 Kafka 自带的 Kafka Raft 模式替代 ZooKeeper),以及启动 Kafka 服务。以下是一个但基于 Linux 的典型安装流程,可以根据需要改装到其…...

Centos7-rpm包管理器方式安装MySQL 5.7.25
前言 本文用于学习通过Mysql压缩包在centos7中安装和配置的过程以及过程中碰到的Bug解决。 Mysql安装包下载和上传 MySQL :: Download MySQL Community Server (Archived Versions)https://downloads.mysql.com/archives/community/访问Mysql官方下载站,选择对应的…...

Project Online 协作版部署方案
目录 前言 第一部分:为什么选择Project Online? 一、核心优势 二、适用场景 第二部分:部署前的准备工作 一、需求分析 二、账户和权限管理 三、培训与支持 第三部分:Project Online 的核心功能 一、项目创建与管理 二、资源管理 三、团队协作 四、风险管理 五…...

小米 13 Ultra机型工程固件 资源预览与刷写说明 步骤解析
小米 13 Ultra机型---机型代码为ishtar 。工程固件可以辅助修复格机或者全檫除分区后的基带修复。可以用于修复TEE损坏。以及一些分区的底层修复。此款固件也可以为更换UFS后的底包。 通过博文了解 1💝💝💝-----此机型工程固件的资源刷写注意事项 2💝💝💝-----此…...

Goweb预防XSS攻击
XSS攻击示例 假设您有一个简单的Web应用程序,其中包含一个用户输入表单,用户可以在其中输入他们的名字,然后这个名字会被显示在页面上。攻击者可以在表单中输入恶意的JavaScript代码,如,如果应用程序没有对这个输入进…...
)
ICM20948 DMP代码详解(36)
接前一篇文章:ICM20948 DMP代码详解(35) 上一回讲到了icm20948_sensor_setup() ---> inv_icm20948_initialize_auxiliary函数 ---> inv_icm20948_set_slave_compass_id函数,本回开始,就对于inv_icm20948_set_sla…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
