二叉树的链式结构和递归程序的递归流程图
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前学习二叉链。

普通二叉树的增删查改没有意义。如果是为了存储数据,线性表更简单,二叉树更复杂,并且插入删除也不好定义。有意义的是通过二叉树引出搜索树,搜索树又有AVL树和红黑树。再搜索树中查找一个节点最多找高度次。
深度优先:前中后序遍历 一般借助递归
广度优先:层序遍历 一般借助队列
typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;// 二叉树前序遍历 递归
void PrevOrder(BTNode* root)
{if(root == NULL){printf("NULL ");return;}// 根 左 右子树 递归 递归过程图在下方printf("%c ",root->data);PrevOrder(root->left);PrevOrder(root->right);
}// 二叉树中序遍历
void InOrder(BTNode* root)
{if(root == NULL){printf("NULL ");return;}// 左 根 右子树 递归 递归过程图在下方InOrder(root->left);printf("%c ",root->data);InOrder(root->right);
}// 二叉树后序遍历
void PostOrder(BTNode* root)
{if(root == NULL){printf("NULL ");return;}// 左 右 根 递归 递归过程图在下方PostOrder(root->left);PostOrder(root->right);printf("%c ",root->data);
}
// 求节点的个数
int TreeSize(BTNode* root)
{// root不是NULL,则个数为左节点个数+右节点个数+1(加的1就是对本节点个数加上去)return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
// 求叶子结点的个数
// 1.NULL return 0 2.叶子 return 1 3.非空且不是叶子 reutrn 左子树叶子节点个数+右子树叶子节点个数
int TreeLeefSize(BTNode* root)
{if(root == NULL)return 0;if(root->left == NULL && root->right == NULL)return 1;return TreeLeefSize(root->left) + root->left(root->right);
}
// 求第K层节点的个数 设K=3 化解为左子树的第K-1(2)层和右子树的第k -1(2)层
int TreeKLeefSize(BTNode* root, int k)
{if(root == NULL)return 0;if(k == 1)return 1;return TreeKLeefSize(root->left, k-1) + TreeKLeefSize(root->right, k-1);
}
// 查找树里面值为X的那个节点 1.root == NULL return NULL
// 2.root 不是要找的 先找左树 左树如果没有再找右树 3.左右都没有则当前树没找到 return null
BTNode* TreeFind(BTNode* root, BTDataType x)
{if(root == NULL)return NULL;// 我就是x则返回if(root->data == x){return root;}// 不是x先在左边找再在右边找BTNode* lret = TreeFind(root->left, x); // 找到了返回root 没找到返回NULLif(lret)return lret;BTNode* rret = TreeFind(root->right, x); // 找到了返回root 没找到返回NULLif(rret)return rret;// 左右都没找到return NULL;
}
// 二叉树销毁 形参的改变不会影响实参,因此需要二级指针
void BinaryTreeDestory(BTNode** pproot)
{// if(*pproot == NULL)// return;// BinaryTreeDestory(&(*pproot)->left); //先将二级指针转换为一级再取地址变为2级传参// BinaryTreeDestory(&(*pproot)->right);// free(*pproot);// *pproot== NULL;
}
// 一级指针的做法 存在野指针,需要将野指针置空 保持接口一致性
void BinaryTreeDestory(BTNode* root)
{if(root == NULL)return;BinaryTreeDestory(root->left); //先将二级指针转换为一级再取地址变为2级传参BinaryTreeDestory(root->right);free(root);
}
// 创建节点
BTNode* CreateTreeNode (BTDataType x)
{BTNode* n1 = (BTNode*)malloc(sizeof(BTNode));n1->data = x;n1->left = NULL;n1->right = NULL:return node;
}
int main()
{// 手动连接上图中的树BTNode* A = CreateTreeNode('A');BTNode* B = CreateTreeNode('B');BTNode* C = CreateTreeNode('C');BTNode* D = CreateTreeNode('D');BTNode* E = CreateTreeNode('E');BTNode* F = CreateTreeNode('F');A->left = B;A->right = C;B->left = D;C->left = E;c->right = F;// 二级做法BinaryTreeDestory(&A);// 一级做法BinaryTreeDestory(A);A = NULL;
}下图为PrevOrder的递归过程图。函数调用该板块完成后会返回到使用该板块的语句。前中后序的本质是一样的,就是打印的时机不同。

- 求节点的个数(前序) 1+左树节点个数+右树节点个数
- 求树的高度(后序) max(左树的高度,右树的高度)+1
深度优先:前中后序遍历 一般借助递归
广度优先:层序遍历 一般借助队列
相关文章:

二叉树的链式结构和递归程序的递归流程图
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分…...

研究生如何利用 ChatGPT 帮助开展日常科研工作?
ChatGPT科研 一、 如何精读论文“三步提问法”1.为什么要做这个研究?这个研究是否值得我们做?2.他们怎么做这个研究3.他们发现了什么? 二、如何利用ChatGPT快速精读论文?首先,“三步走之第一步”--为什么要做这个研究&…...

【LLM学习之路】9月16日 第六天
【LLM学习之路】9月16日 第六天 损失函数 L1Loss 可以取平均也可以求和 参数解析 input (N,*) N是batchsize,星号代表可以是任意维度 不是输入的参数,只是描述数据 target 形状要同上 MSELoss平方差 CrossEntr…...
Qt_窗口界面QMainWindow的介绍
目录 1、菜单栏QMenuBar 1.1 使用QMainWindow的准备工作 1.2 在ui文件中设计窗口 1.3 在代码中设计窗口 1.4 实现点击菜单项的反馈 1.5 菜单中设置快捷键 1.6 菜单中添加子菜单 1.7 菜单项中添加分割线和图标 1.8 关于菜单栏创建方式的讨论 2、工具栏QToolBar …...

华为云centos7.9按装ambari 2.7.5 hostname 踩坑记录
华为云centos7.9按装ambari 2.7.5踩坑记录 前言升华总结 前言 一般都是废话,本人专业写bug业余运维。起初找了三台不废弃的台式机,开始重装centos系统,开始了HDP3.1.5Ambari2.7.5安装。 推荐一波好文,一路长绿。跑了一段时间没啥…...
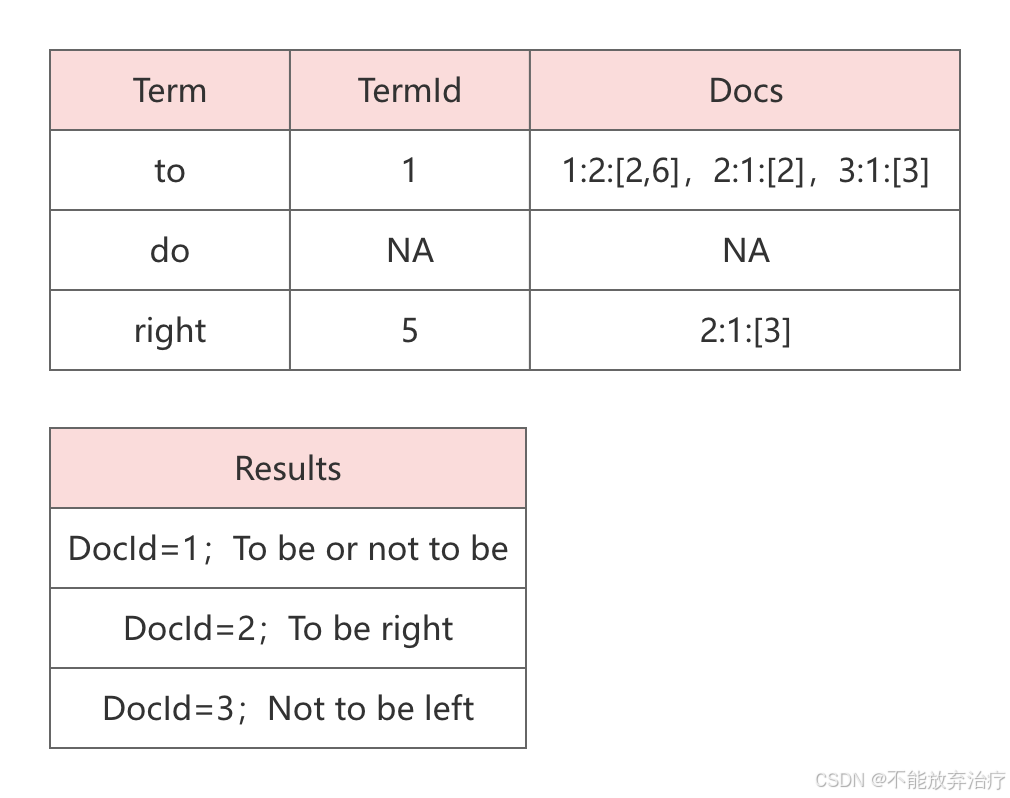
重生之我们在ES顶端相遇第15 章 - ES 的心脏-倒排索引
文章目录 前言为什么叫倒排索引数据结构如何生成如何查询TF、IDF参考文档 前言 上一章,简单介绍了 ES 的节点类型。 本章,我们要介绍 ES 中非常重要的一个概念:倒排索引。 ES 的全文索引就是基于倒排索引实现的。 本章内容建议重点学习&…...

金刚石切削工具学习笔记分享
CVD钻石-合成单晶钻石之一 金刚石具有极高的硬度和耐磨性、较低的摩擦系数、较高的弹性模量、较高的热导率、较低的热膨胀系数、与有色金属的亲和力较小等优点,是目前最硬的工具材料,主要分为单晶金刚石和聚晶金刚石两大类。单晶金刚石又分为天然单晶金…...

【文献阅读】基于原型的自适应方法增强未见到的构音障碍者的语音识别
基于原型的自适应方法增强未见到的构音障碍者的语音识别 文献原文链接 https://www.isca-archive.org/interspeech_2024/wang24x_interspeech.pdf 引言 构音障碍是一种由神经系统疾病或肌肉异常引起的言语障碍,影响了个体清晰发音的能力。这种情况常伴随脑瘫、帕金森病和头部…...

Kafka-Go学习
文章目录 1. **安装 kafka-go**2. **基本概念**3. **kafka-go 基本用法**3.1 创建 Producer(生产者)3.2 创建 Consumer(消费者)3.3 生产者和消费者配置详解生产者配置 (kafka.WriterConfig)消费者配置 (kafka.ReaderConfig) 4. **…...

Nginx反向代理出现502 Bad Gateway问题的解决方案
🎉 前言 前一阵子写了一篇“关于解决调用百度翻译API问题”的博客,近日在调用其他API时又遇到一些棘手的问题,于是写下这篇博客作为记录。 🎉 问题描述 在代理的遇到过很多错误码,其中出现频率最高的就是502&#x…...
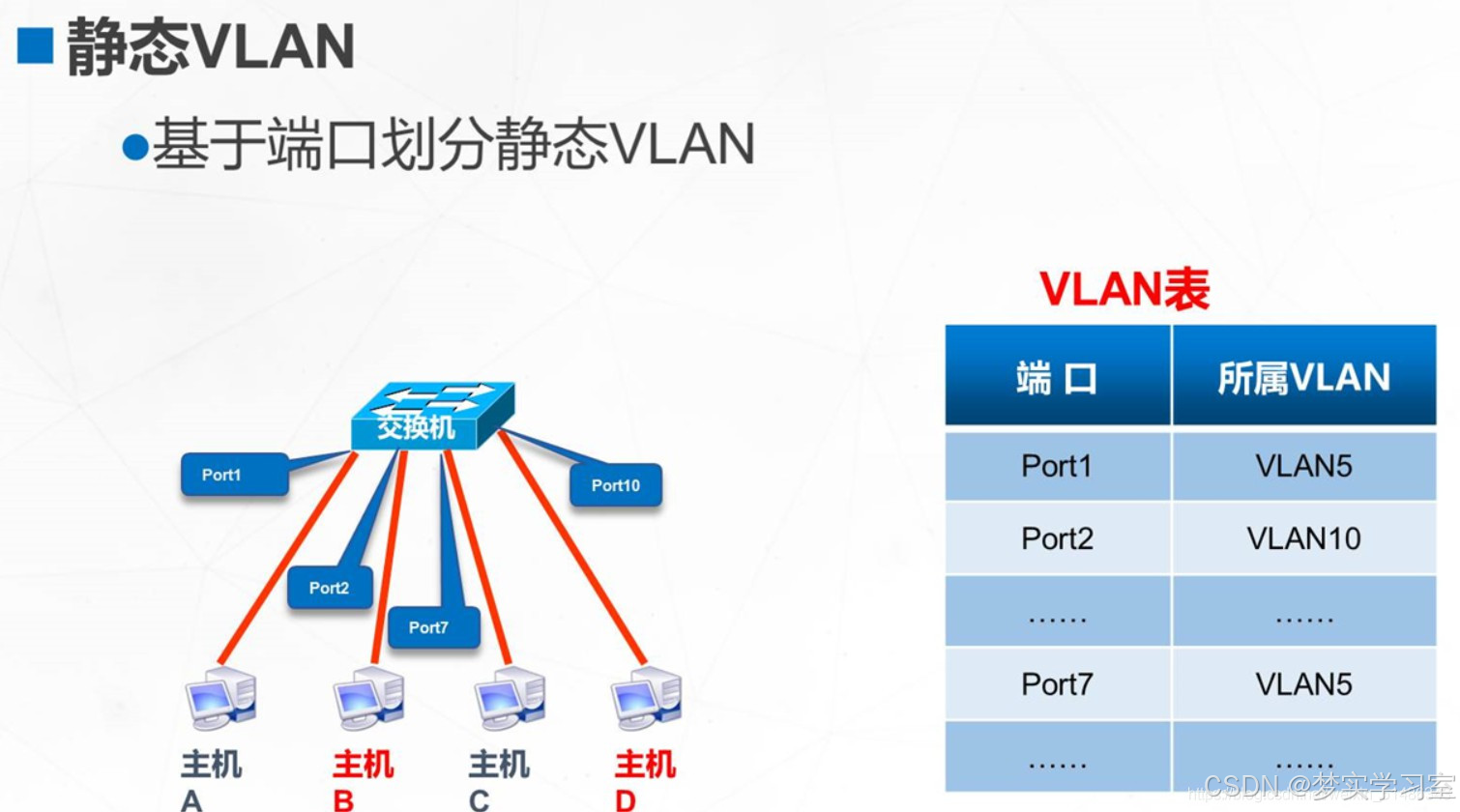
通信工程学习:什么是VLAN虚拟局域网
VLAN:虚拟局域网 VLAN(Virtual Local Area Network,虚拟局域网)是一种将物理局域网在逻辑上划分成多个广播域的通信技术。以下是关于VLAN的详细解释: 一、VLAN虚拟局域网的定义与概述 VLAN通过逻辑方式将网络中的设备…...

python qt5 常用
QT5中如何设置让窗口根据屏幕比例显示设置? desktop QDesktopWidget().screenGeometry() self.resize(int(desktop.width() * 0.3), int(desktop.height()*0.5)) QT5中关于背景穿透问题的处理方式? 场景如下:我们在开发的时候,…...
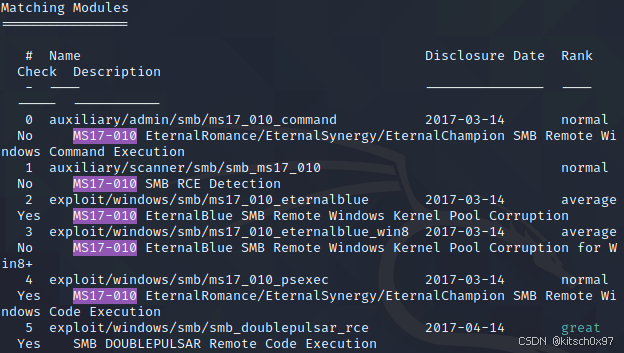
漏洞复现_永恒之蓝
1.概述 永恒之蓝(EternalBlue)是一个影响Windows操作系统的远程代码执行漏洞,编号为CVE-2017-0144,最初由美国国家安全局(NSA)开发并利用,后来被黑客组织Shadow Brokers泄露。该漏洞存在于SMBv…...

PyCharm的使用
PyCharm的入门使用教程 下载和安装PyCharm: 首先,访问JetBrains官方网站(https://www.jetbrains.com/pycharm/)下载PyCharm的最新版本。根据您的操作系统选择合适的版本进行下载。 安装完成后,打开PyCharm。 创建新…...

浅谈C#之AutoResetEvent和ManualResetEvent
一、基本介绍 AutoResetEvent和ManualResetEvent都是同步原语,它们用于线程之间的协调和通信。它们都是从EventWaitHandle类派生的,但它们在重置事件状态的行为上有所不同。 二、简单示例 AutoResetEvent AutoResetEvent是一个自动重置的事件。当一个线…...
【网络安全 | 靶机搭建】修改镜像源、更新软件源、安装git、更改python版本等
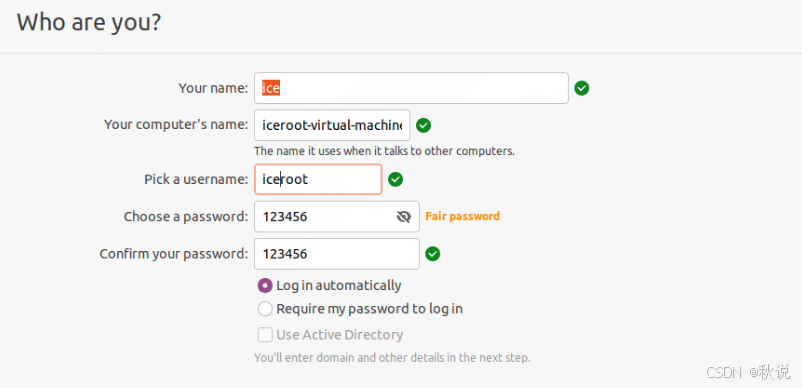
文章目录 0x00、必要准备0x01、修改镜像源0x02、更新软件源并清除缓存0x03、安装git0x04、更改默认Python版本为python30x05、安装增强功能0x06、vmware虚拟机导出iso0x00、必要准备 安装虚拟机时必须保存用户名、密码,用于后续操作,可以截图保存: 以下内容按个人需要进行配…...
VuePress搭建文档网站/个人博客(详细配置)主题配置
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

Go语言笔记
目录 一、变量声明 二、流程控制 if(条件判断) for(循环结构) Switch(简化if) goto(跳出循环) 三、运算符 1、算数运算符 2、关系运算符 3、逻辑运算符 4、位运算符 5、…...

java缓存介绍
在Java编程中,缓存技术是一种非常有效的优化手段,用于减少数据访问的延迟和提高应用性能。缓存技术通过存储数据的副本在内存中,使得后续对相同数据的请求能够直接从内存中快速获取,而不需要再次进行耗时的磁盘访问或网络请求。 缓…...

react中diff的选择性子树渲染
在React中,组件的渲染是高效的,这得益于React的虚拟DOM(Virtual DOM)和diff算法。React的diff算法主要用于比较旧虚拟DOM树和新虚拟DOM树之间的差异,并仅更新实际DOM中需要变化的部分,从而提高性能。 关于…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...
