二分算法——优选算法
个人主页:敲上瘾-CSDN博客
个人专栏:游戏、数据结构、c语言基础、c++学习、算法
本章我们来学习的是二分查找算法,二分算法的应用非常广泛,不仅限于数组查找,还可以用于解决各种搜索问题、查找极值问题等。在数据结构和算法中,它是基础且重要的算法之一。
接下来我准备了三个题来引出并学习该算法,最后来做总结。
目录
一、二分查找
1.题目解析
2.算法原理
3.代码编写
二、查找元素的首末位置
1.题目解析
2.算法原理
3.代码编写
三、寻找峰值
1.题目解析
2.算法原理
3.代码编写
四、总结
一、二分查找
1.题目解析

该题目要求是给一个元素target然后在升序数组nums中找到该元素的下标,若不存在则返回-1。题目要求简单易懂就不再多讲,这里要注意两个点:(1)、数组是升序的。(2)、需要返回的是元素下标。
2.算法原理
对于该题最容易想到的解法就是把数组从头到尾遍历一遍,时间复杂度为O(N)。
解法二:因为这个数组是有序的所以我们可以用二分的思想,首先使用三个指针(这里指的是数组的下标)left,right,mid,其中left和right维护一段区间,把目标值锁定到[left,right]区间内。mid表示区间的中心下标,把区间一分为二。
接下来锁定target的位置:如果target小于mid下标指向的元素,那么因为数组是升序,所以target一定在区间[left,mid]中,即right更新为mid,然后更新mid( mid=left+(right-left)/2 )。 如果target大于mid指向元素,那么target一定在区间[mid,right]中,即把left更新为mid,然后更新mid。重复操作直到left>right。
如下:

该算法的时间复杂度为logN,证明如下:

3.代码编写
class Solution
{
public:int search(vector<int>& nums, int target){int left=0,right=nums.size()-1;while(left<=right){int mid=left+(right-left)/2;if(nums[mid]>target) right=mid-1;else if(nums[mid]<target) left=mid+1;else return mid;}return -1;}
};二、查找元素的首末位置
1.题目解析

该题的题目要求与上一题类似,都是在升序数组中查找元素,不过该题查找的是元素第一次出现的位置和最后一次出现的位置。这里还要求时间复杂度为O(logN),这里就很明显地提示了该题要使用二分算法。
2.算法原理
同样的此题可以使用暴力枚举来解决,不过时间复杂度为O(N),根据上题的经验这里我们还是考虑使用二分法。不过也很容易发现把上面的算法原模原样搬过来是解决不了该道题的,我们只能找到target元素的是无法锁定它第一次出现的位置和最后一次出现的位置。我们可以用以下解法:
左边界查找:
当mid指向的元素为target的时候,不用返回,而是让right更新为mid,mid指向元素大于target时同样更新right为mid,即可以合并为
if(nums[mid]>=target) right=mid;
当mid指向元素小于target时left更新为mid+1,重复该操作就可以把数组右边的target忽略,锁定最左边的target。这里做循环的时候需要注意循环条件不能是left<=rigth,如果是left<=right就可能使mid一直赋值给right从而进入死循环,所以我们使用left<right。
右边界查找:
当mid指向的元素为target的时候,不用返回,而是让left更新为mid,mid指向元素小于target时同样更新left为mid,即可以合并为
if(nums[mid]<=target) left=mid;
当mid指向元素大于target时right更新为mid-1,重复该操作就可以把数组左边的target忽略,锁定最右边的target。这里做循环的时候同样需要注意循环条件只能是left<rigth。
注意:当元素只有两个时使用mid=left+(right-left)/2计算的mid就是第一个元素,那么也就是mid==left,如果mid指向的元素为target时把mid赋值给left(即left=mid)相当于什么也没干,程序同样会进入死循环。所以我们使用mid=left+(right-left+1)/2计算mid。
以上的两个查找法几乎可以解决所有的二分算法题,可以作为一个模板记忆,在总结部分我会给出模板。
3.代码编写
class Solution
{
public:vector<int> searchRange(vector<int>& nums, int target) {if(nums.size()==0) return {-1,-1};int left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]>=target) right=mid;else left=mid+1;}if(nums[left]!=target) return {-1,-1};int n=left;right=nums.size()-1;while(left<right){int mid=left+(right-left+1)/2;if(nums[mid]<=target) left=mid;else right=mid-1;}return {n,left};}
};三、寻找峰值
1.题目解析

该题要求我们返回任意峰值,比如把数组元素抽象成连续的数据如下:

需要返回以上红圈部分的任意一点, 也就是该元素至少要满足它左边的第一个元素和右边的第一个元素都要小于它。
注意:题目给的信息nums[-1]和nums[n]为负无穷,所以不要忽略以下情况:

2.算法原理
这题同样可以使用暴力枚举,时间复杂度为O(N),该解法就不再多讲。
这个题与上两个题有一个很大的区别是该数组并不是有序的,但是没关系该题同样可以使用二分的思想,注意很多人会误认为二分算法只能用在有序的数组中,而事实并不局限于此,只需要找到数据的二段性即可,如该题我们可以这样:

该方法也就是上一题的右边界查找,当然也可以使用左边界查找的方法,但用朴素的二分查找解决不了该题。
3.代码编写
class Solution
{
public:int findPeakElement(vector<int>& nums) {int left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]>nums[mid+1]) right=mid;else left=mid+1;}return left;}
};四、总结
1、二分算法并不局限于数组有序,只要找到数据的二段性即可使用二分算法。
2、二分算法模板
2.1.朴素二分模板
while(left<=right) {int mid=left+(right-left)/2;if(...) left=mid+1;else if(...) right=mid-1;else ... }2.2.左边界查找模板
while(left<right) {int mid=left+(right-left)/2;if(...) left=mid+1;else right=mid; }2.3.右边界查找模板
while(left<right) {int mid=left+(right-left+1)/2;if(...) left=mid;else right=mid-1; }
相关文章:

二分算法——优选算法
个人主页:敲上瘾-CSDN博客 个人专栏:游戏、数据结构、c语言基础、c学习、算法 本章我们来学习的是二分查找算法,二分算法的应用非常广泛,不仅限于数组查找,还可以用于解决各种搜索问题、查找极值问题等。在数据结构和算…...

Kafka 的基本概念
一、Kafka 主要用来做什么 作为消息系统:Kafka 具备系统解藕,流量削峰,缓冲,异步通信,扩展性,可恢复性等功能,以及消息顺序性保障和回溯消费 作为存储系统:Kafka 把消息持久化到磁…...
《粮油与饲料科技》是什么级别的期刊?是正规期刊吗?能评职称吗?
问题解答 问:《粮油与饲料科技》是不是核心期刊? 答:不是,是知网收录的第一批认定 学术期刊。 问:《粮油与饲料科技》级别? 答:省级。主管单位:中文天地出版传媒集团股份有限公司…...

Python之一些列表的练习题
1.比较和对比字符串、列表和元组。例如,它们可以容纳哪类内容以及在数据结构上可以做哪些操作。 1. 内容类型:- 字符串: 只能包含字符(文本)。- 列表: 可以包含任意类型的数据,如数字、字符串、其他列表等。- 元组: 可以包含任意类型的数据,与列表类似。3. 操作:(1…...

MoFA: 迈向AIOS
再一次向朋友们致以中秋的祝福! MoFA (Modular Framework for Agents)是一个独特的模块化AI智能体框架。MoFA以组合(Composition)的逻辑和编程(Programmable)的方法构建AI智能体。开发者通过模版的继承、编程、定制智能体…...

c语言中define使用方法
在C语言中,#define指令是预处理指令,用于定义宏。其常用格式是: 定义常量: #define 常量名 常量值 例子: #define PI 3.14159 #define MAX_SIZE 100 这里,PI和MAX_SIZE在代码中会被替换为其对应的值。没有…...

尚品汇-秒杀商品定时任务存入缓存、Redis发布订阅实现状态位(五十一)
目录: (1)秒杀业务分析 (2)搭建秒杀模块 (3)秒杀商品导入缓存 (4)redis发布与订阅实现 (1)秒杀业务分析 需求分析 所谓“秒杀”࿰…...
——spring-boot-devtools)
第十一章 【后端】商品分类管理微服务(11.4)——spring-boot-devtools
11.4 spring-boot-devtools 官网:https://docs.spring.io/spring-boot/reference/using/devtools.html Spring Boot DevTools 是 Spring Boot 提供的一组易于使用的工具,旨在加速开发和测试过程。它通过提供一系列实用的功能,如自动重启、实时属性更新、依赖项的热替换等,…...
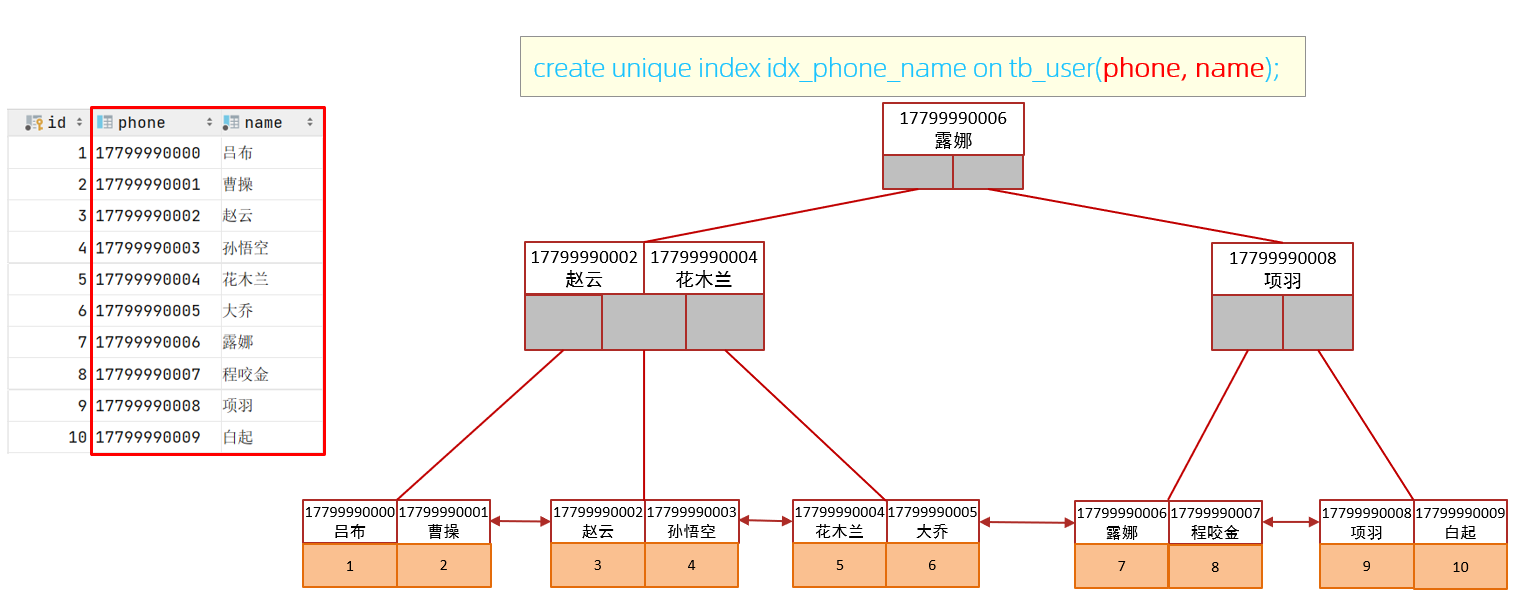
MySQL篇(索引)(持续更新迭代)
目录 一、简介 二、有无索引情况 1. 无索引情况 2. 有索引情况 3. 优劣势 三、索引结构 1. 简介 2. 存储引擎对于索引结构的支持情况 3. 为什么InnoDB默认的索引结构是Btree而不是其它树 3.1. 二叉树(BinaryTree) 3.2. 红黑树(RB&a…...

通用接口开放平台设计与实现——(31)API服务线程安全问题确认与修复
背景 在本系列的前面一篇博客评论中,有小伙伴指出,API服务存在线程安全问题: https://blog.csdn.net/seawaving/article/details/122905199#comments_34477405 今天来确认下,线程是否安全?如不安全,如何…...
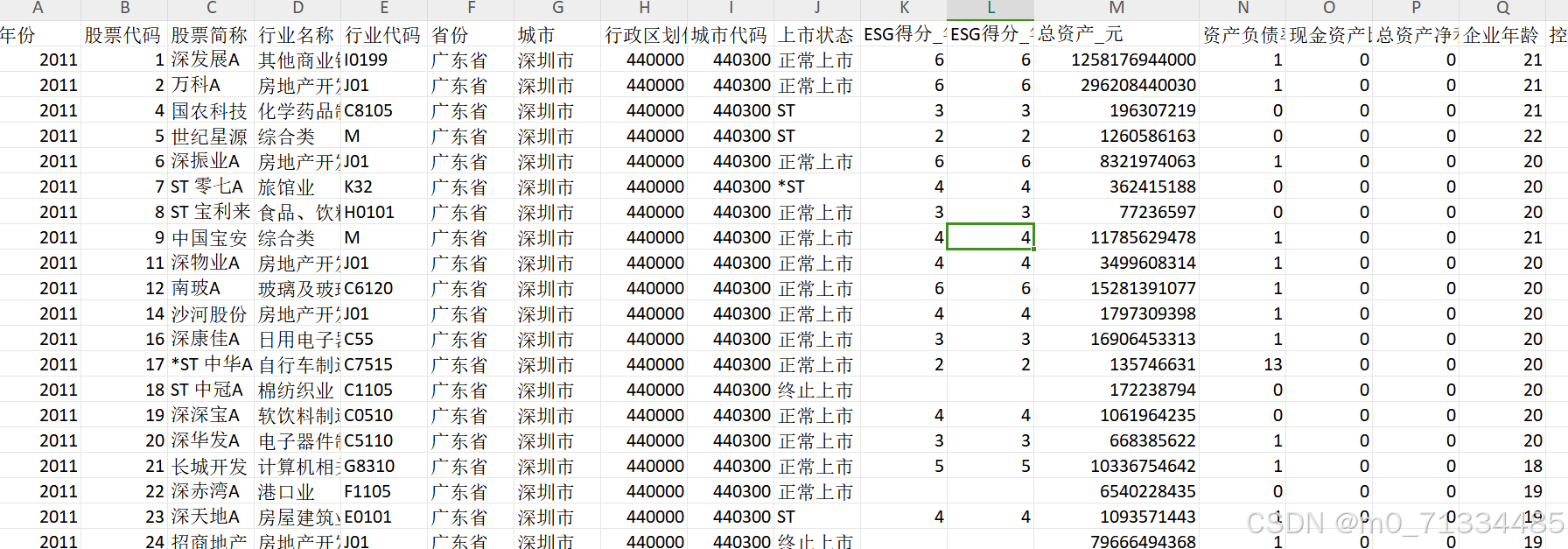
2011-2022年数字金融与企业ESG表现:效应、机制与“漂绿”检验(内含原始数据+处理代码)
2011-2022年数字金融与企业ESG表现:效应、机制与“漂绿”检验(内含原始数据处理代码) 1、时间:2011-2022年 2、来源:上市公司年报、华证ESG、北大数字普惠金融 3、指标:年份、股票代码、股票简称、行业名…...

mysql配置相关命令
一、允许所有人访问: -- 1.切换至mysql库 use mysql;-- 2.查看用户表 SELECT Host,User FROM user;-- 3.修改字段 UPDATE user SET Host % WHERE User root;-- 4.刷新权限 flush privileges;二、修改加密方式 -- 1.切换至mysql库 use mysql;-- 2.查看用户表 SELEC…...
【自用软件】IDM下载器 Internet Download Manager v6.42 Build 10
下载IDM&pj安装教程 Internet Download Manager,简称 IDM,是国外的一款优秀下载工具。目前凭借着下载计算的速度优势在外媒网站中均受好评,现在已被多数国人熟知。Internet Download Manager 提升你的下载速度最多达5倍,安排下…...

Kafka集群扩容(新增一台kafka节点)
kafka集群扩容、kafka topic迁移 现有环境 IP组件角色192.168.17.51kafka01broker1192.168.17.52kafka02broker2192.168.17.53kafka03broker3 扩容之后环境 IP组件角色192.168.17.51kafka01broker1192.168.17.52kafka02broker2192.168.17.53kafka03broker3192.168.17.54ka…...

作文笔记15 点面结合
事件中场面写作方法:点面结合(对毛主席的描写和三十万群众的描写间插进行)。好处是强化描写的层次感,既有整体形象描写,又凸显人物个性特点。 景色描写方法:动态描写,静态描写,动静…...
问题)
Spring Boot-国际化(I18N)问题
Spring Boot 国际化(I18N)问题及其解决方案 1. 引言 随着全球化的推进,软件开发中的国际化(I18N)需求日益增长。国际化是指通过设计应用程序,使其能够轻松适应不同语言和地区的需求,而无需修改…...

8. 防火墙
8. 防火墙 (1) 防火墙的类型和结构 防火墙的类型和结构可以根据其在网络协议栈中的过滤层次和实现方式进行分类。常见的防火墙类型包括: 包过滤防火墙:工作在网络层(OSI模型的第3层),主要检查IP包头的信息,如源地址、目的地址、端口号等。电路级网关防火墙:工作在会话层…...

C语言循环学习
作为初学者,学习C语言中的循环结构是非常重要的,它们能让你轻松地重复执行代码。在C语言中,常用的循环结构主要有for循环和while循环。我们将从基本概念开始,逐步讲解如何使用这两种循环,并通过示例帮助你理解和练习。…...
分享-3)
职业技能大赛-自动化测试笔记(Unitest)分享-3
前言 UnitTest是Python标准库中的一个模块,用于编写和执行单元测试。它提供了一组断言方法,用于验证代码的输出和状态是否符合预期。通过UnitTest框架,我们可以编写可重复执行的测试用例,并使用命令行工具或IDE轻松运行这些测试。在大多数情况下,UnitTest框架已经包含在Py…...
rocky9.2的lvs的NAT模式下的基本使用的详细示例
文章目录 前言什么是LVS?(Linux Virtual Server)LVS的组成1. 负载均衡器(Load Balancer)2. 后端服务器池(Real Servers)3. IPVS(IP Virtual Server)4. 调度算法(Schedul…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
