数据结构-树(基础,分类,遍历)
数据结构-树
1.什么是树?
在计算机科学中,树是一种常用的非线性数据结构,用于表示具有层次关系的数据。与线性数据结构(如数组和链表)不同,树结构以节点(Nodes)和边(Edges)组成,通过根节点(Root Node)进行组织。每个节点可以有零个或多个子节点,形成一系列层级结构。
树的基本术语包括:
- 根节点(Root):树的最上层节点,没有父节点。
- 节点(Node):树中的基本单元,包含数据和指向子节点的引用。
- 子节点(Child):直接连接到某一节点的节点。
- 父节点(Parent):直接连接到子节点的节点。
- 叶节点(Leaf):没有子节点的节点。
- 深度(Depth):节点到根节点的路径长度。
- 高度(Height):节点到其最远叶节点的路径长度。
2.树的类型
- 二叉树(Binary Tree):每个节点最多有两个子节点(左子节点和右子节点)。
- 二叉搜索树(Binary Search Tree, BST):左子树的所有节点值小于根节点值,右子树的所有节点值大于根节点值。
- 平衡树(Balanced Tree):如 AVL 树和红黑树,保持树的高度平衡,以优化插入、删除和查找操作的时间复杂度。
2.1. 二叉树(Binary Tree)

定义:二叉树是一种每个节点最多有两个子节点的树形结构。每个节点通常包含三个部分:数据、左子节点、右子节点。
特点:
- 结构:每个节点有至多两个子节点,通常称为左子节点和右子节点。
- 类型:包括满二叉树(每个节点都有两个子节点)、完全二叉树(除了最底层外,所有层都是满的)和不完全二叉树(节点可能只有一个子节点)。
完全二叉树和非完全二叉树:

用途:广泛应用于表达结构性的数据,例如表达式树、决策树等。
2.2. 二叉搜索树(Binary Search Tree, BST)

定义:二叉搜索树是一种特殊的二叉树,其中每个节点的左子树包含小于该节点值的节点,右子树包含大于该节点值的节点。(值)
特点:
- 性质:对于每个节点,左子树的所有节点值小于该节点值,右子树的所有节点值大于该节点值。
- 操作:插入、删除和查找操作可以在平均 O(log n) 时间复杂度下完成,前提是树是平衡的。
用途:常用于实现高效的查找、插入和删除操作。
2.3. 平衡树(Balanced Tree)
定义:平衡树是一种自我调整的二叉搜索树,确保树的高度在一个合理范围内,从而优化操作效率。
类型:
- AVL 树:一种严格平衡的二叉搜索树,其中每个节点的左右子树高度差最多为1。插入和删除操作后,可能需要进行旋转来保持平衡。
- 红黑树:一种较宽松的平衡树,其中每个节点都有一个颜色属性(红色或黑色),并且遵循一系列规则来确保树的平衡。红黑树在插入和删除时也进行必要的旋转和重新着色。
特点:
- AVL 树:高度更严格平衡,查询操作通常较快,但插入和删除的旋转次数可能较多。
- 红黑树:维护平衡较为宽松,插入和删除操作的复杂度较低,但查询操作可能稍慢。
用途:用于实现具有自平衡特性的高效数据结构,如Java的 TreeMap 和 TreeSet。
3.二叉树的存储
二叉树的存储结构通常有两种方式:顺序存储和链式存储。顺序存储适用于完全二叉树,而链式存储则更为灵活,适用于不完全二叉树。二叉树的遍历方式包括前序遍历、中序遍历、后序遍历和层序遍历(广度遍历),这些遍历方式按照不同的顺序访问树的节点。
4.二叉树的遍历
二叉树的遍历是指按某条搜索路径访问树中的每个结点,使得每个结点均被访问一次。
1)先序遍历
若二叉树为空,则返回,否则先访问根节点,再先序遍历左子树,再先序遍历右子树。
void PreOrderVisit(BiTree T) {if (T != NULL) {visit(T);PreOrderVisit(T->lchild);PreOrderVisit(T->rchild);}
}
2)中序遍历
若二叉树为空,则返回,否则先中序遍历左子树,再访问根节点,再中序遍历右子树。
void InOrderVisit(BiTree T) {if (T != NULL) {InOrderVisit(T->lchild);visit(T);InOrderVisit(T->rchild);}
}
3)后序遍历
若二叉树为空,则返回,否则先后序遍历左子树,再后序遍历右子树,再访问根节点。
void PostOrderVisit(BiTree T) {if (T != NULL) {PostOrderVisit(T->lchild);PostOrderVisit(T->rchild);visit(T);}
相关文章:

数据结构-树(基础,分类,遍历)
数据结构-树 1.什么是树? 在计算机科学中,树是一种常用的非线性数据结构,用于表示具有层次关系的数据。与线性数据结构(如数组和链表)不同,树结构以节点(Nodes)和边(Ed…...

CodeGeeX4:程序员的高效助手,多语言代码生成神器!
你是否曾在编写代码时,为复杂的语法、逻辑错误而绞尽脑汁?或是在面对多个编程语言的切换时,感觉脑子快要爆炸?别担心!一款全新的多语言代码生成神器——CodeGeeX4,正悄然成为程序员们的“救命稻草”。它不仅…...

小程序组件间通信
文章目录 父传子子传父获取组件实例兄弟通信 父传子 知识点: 父组件如果需要向子组件传递指定属性的数据,在 WXML 中需要使用数据绑定的方式 与普通的 WXML 模板类似,使用数据绑定,这样就可以向子组件的属性传递动态数据。 父…...

Homebrew安装与切换下载源
一、安装 1.Homebrew的官网地址 https://brew.sh/zh-cn/ 2.执行命令行安装 /bin/bash -c “$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)” 3.无法连接到https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh的地址 解决…...

C#回调函数
1、定义并初始化委托 public delegate void CallbackDelegate(string message);//定义一个委托类型CallbackDelegate callbackDelegate;//声明一个委托对象/// <summary>/// 定义委托对应的函数/// </summary>/// <param name"str"></param>…...

Matplotlib绘制热力图
热力图(Heatmap)是一种使用颜色来表示数值强度的数据可视化工具。它常用于以下场景: 热力图的适用场景 数据的相关性分析:在统计学中,热力图常用于展示变量之间的相关性,尤其是当数据量较大时,…...

手写SpringMVC
1、开发HspDispatcherServlet 2、完成客户端/浏览器可以请求控制层 目的:发出url请求时,经过前端控制器,找到Monster的List方法,把结果再打回去 3、从web.xml动态获取hspspringmvc.xml 4、完成自定义Service注解功能 目的&…...
(18))
mysql学习教程,从入门到精通,SQL 删除数据(DELETE 语句)(18)
1、SQL 删除数据(DELETE 语句) 在编写SQL中的DELETE语句时,需要非常小心,因为一旦执行,被删除的数据就无法恢复了(除非你有备份)。DELETE语句用于从数据库表中移除一条或多条记录。这里&#x…...

周边游小程序开发
开发一个周边游小程序是一个既有趣又富有挑战性的项目,它可以帮助用户发现周边的旅游景点、活动、美食和住宿等,提升用户的旅游体验。以下是开发周边游小程序的基本步骤和一些建议: 1.市场调研与需求分析 目标用户定位:确定你的用…...

初级前端面试
1.介绍自己 2.介绍一下之前做过的项目以及接触的业务 3.最近学的技术,接触的是哪一块(回答了vue3) 4.vue3在什么时候调用接口 beforeCreate 在实例初始化之后,数据观测 (data observer) 和 event/watcher 事件配置之前被调用。 用…...

微软AI核电计划
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

图片马赛克处理(Java)
1.需求 给图片的指定区域打码给整张图片打码马赛克方格取色支持中心点取色和随机取色马赛克支持灰度处理 2.源码 package com.visy.utils;import javax.imageio.ImageIO; import java.awt.*; import java.awt.image.BufferedImage; import java.io.File; import java.io.IOE…...

python+selenium实现自动联网认证,并实现断网重连
pythonselenium实现自动联网认证,并实现断网重连 echo off python “E:\autoD\auto_login.py” 要使自动登录脚本在系统重启后自动运行,你可以使用Windows的任务计划程序来设置。以下是详细的步骤: 1. 保存脚本 首先,将你的Py…...
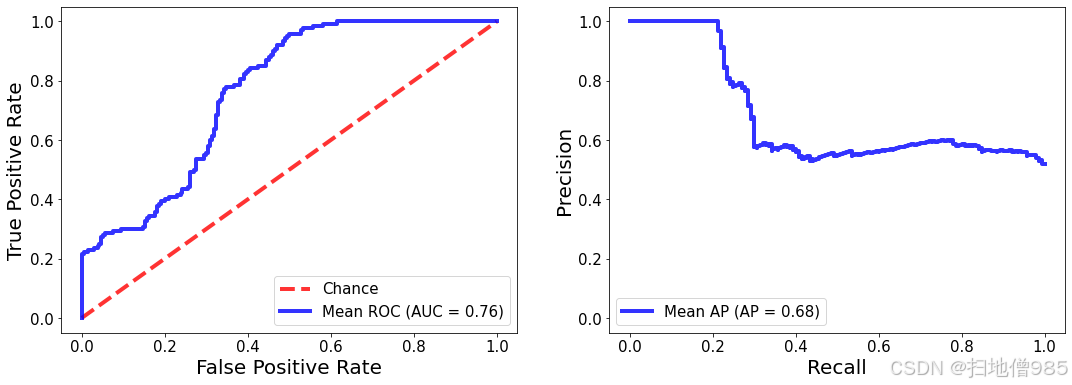
基于机器学习的注意力缺陷/多动障碍 (ADHD)(python论文+代码)HYPERAKTIV
简述 医疗保健领域的机器学习研究往往缺乏完全可重复性和可比性所需的公共数据。由于患者相关数据附带的隐私问题和法律要求,数据集往往受到限制。因此,许多算法和模型发表在同一主题上,没有一个标准的基准。因此,本文提出了一个公…...
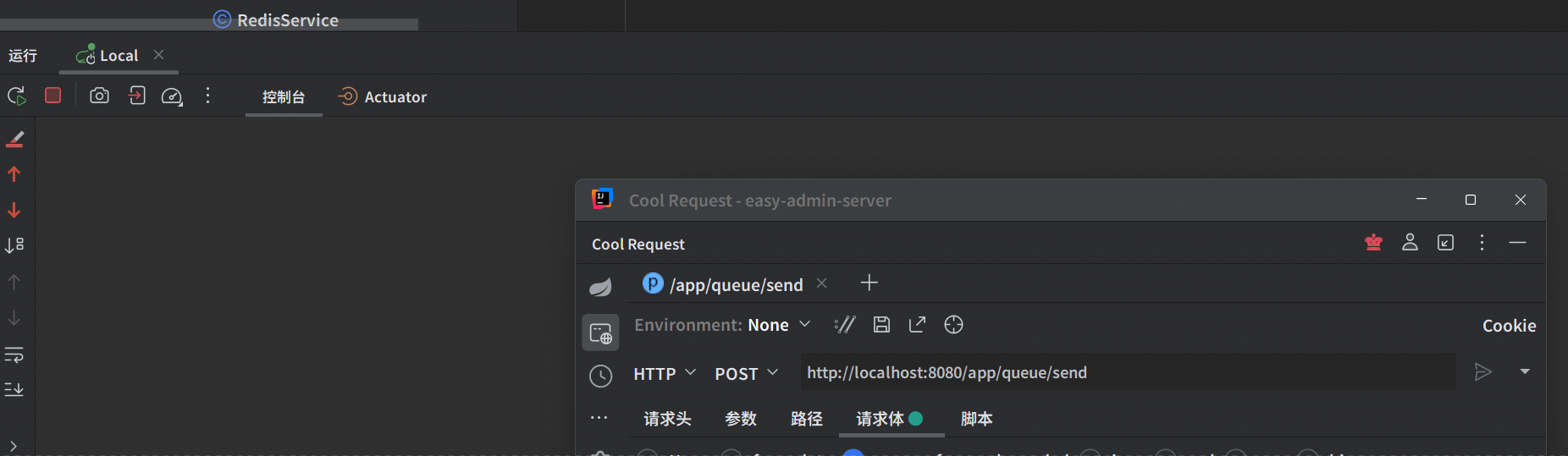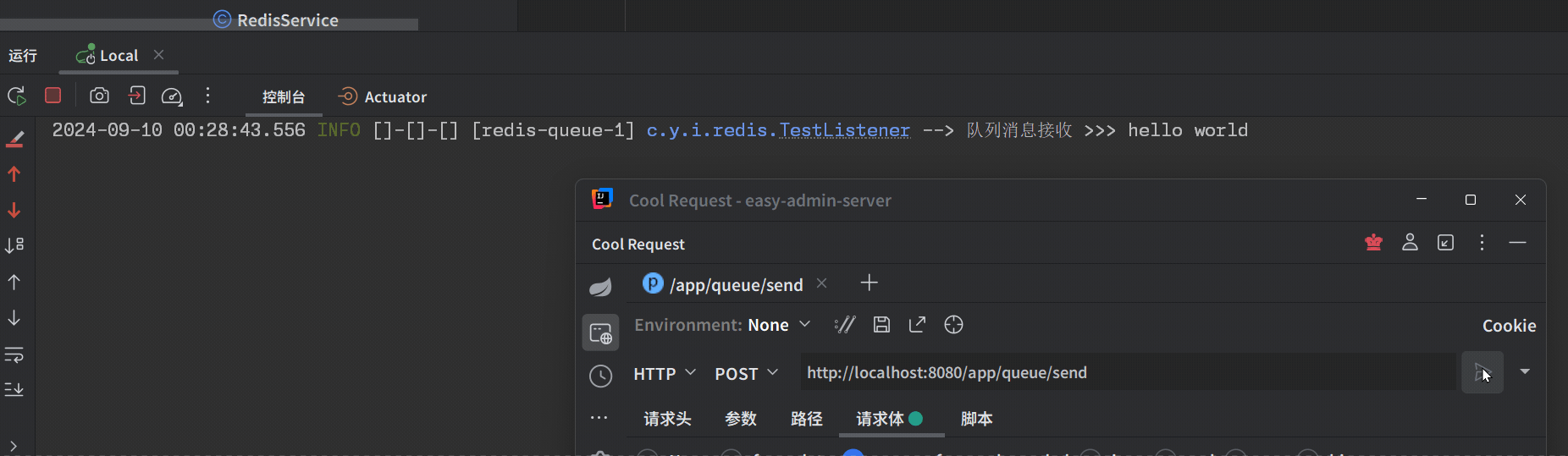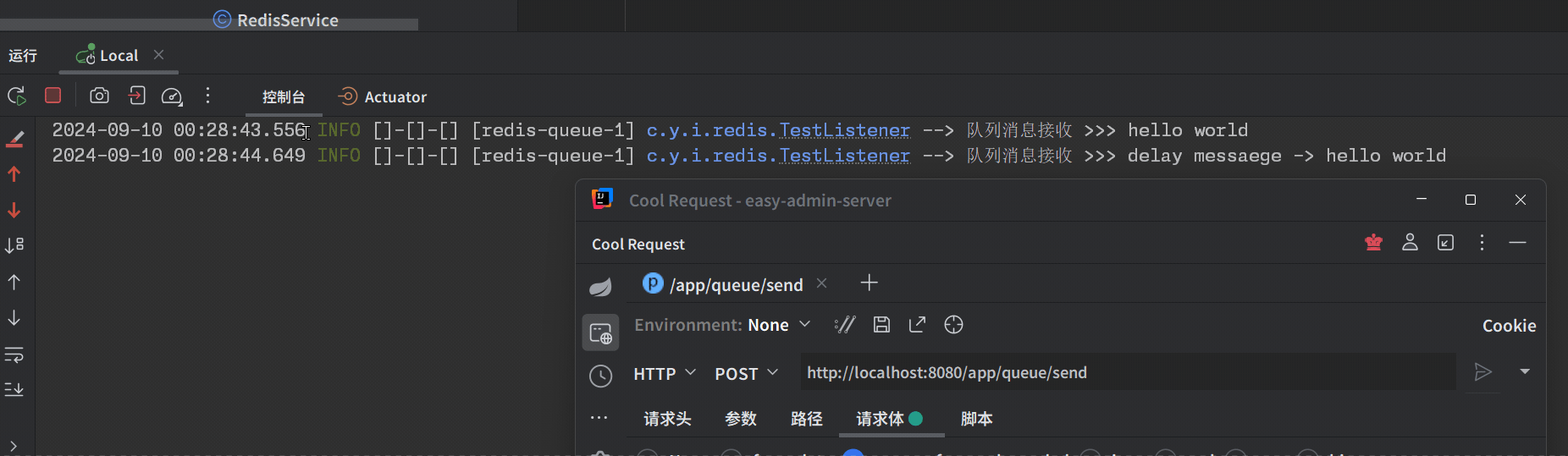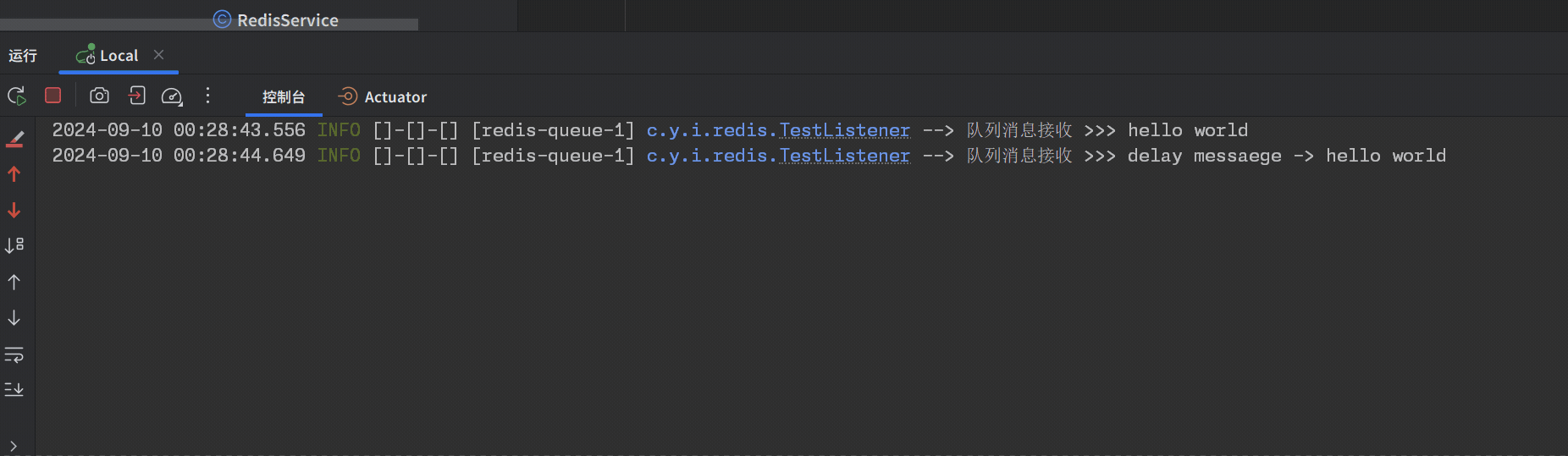
Spring Boot 集成 Redisson 实现消息队列
包含组件内容 RedisQueue:消息队列监听标识RedisQueueInit:Redis队列监听器RedisQueueListener:Redis消息队列监听实现RedisQueueService:Redis消息队列服务工具 代码实现 RedisQueue import java.lang.annotation.ElementTyp…...

go语言Map详解
Map Go语言中提供的映射关系容器为map,其内部使用散列表(hash)实现 map是一种无序的基于key-value的数据结构,Go语言中的map是引用类型,必须初始化才能使用。 它提供了高效的查找、插入和删除操作,非常适…...

C++——已知数组a[6]={1,3,5,7,9};输入一个数值,要求按照现有排序规律将它放入数组当中。
没注释的源代码 #include <iostream> using namespace std; int main() { int a[6]{1,3,5,7,9}; int n,i,j; cout<<"请输入一个数值:"; cin>>n; for(int i0;i<4;i) { if(n<a[i]) { …...
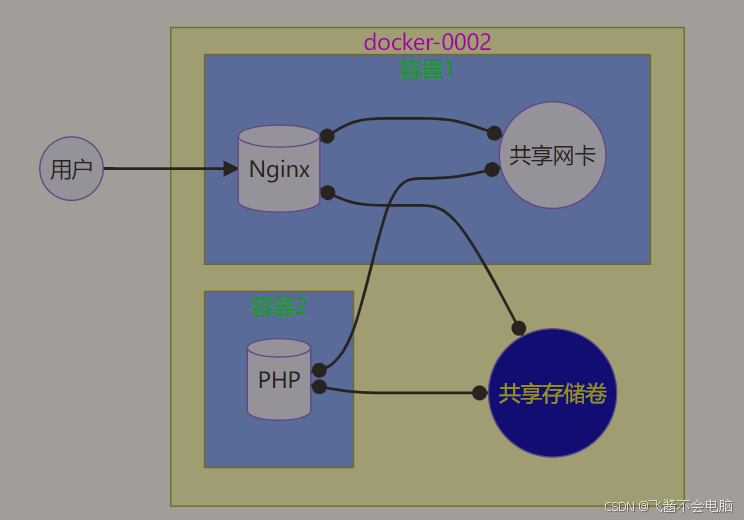
云计算第四阶段---CLOUD Day7---Day8
CLOUD 07 一、Dockerfile详细解析 指令说明FROM指定基础镜像(唯一)RUN在容器内执行命令,可以写多条ADD把文件拷贝到容器内,如果文件是 tar.xx 格式,会自动解压COPY把文件拷贝到容器内,不会自动解压ENV设置…...
深入解析ThingsBoard与ThingsKit物联网平台的差异
VS 在物联网(IoT)领域,平台的选择对于企业来说至关重要。本文将深入探讨ThingsBoard社区版与ThingsKit企业版这两个物联网平台的差异,帮助读者更好地理解它们的特色和适用场景。 系统相同点 首先,ThingsBoard社区版和ThingsKit企业版都基于…...
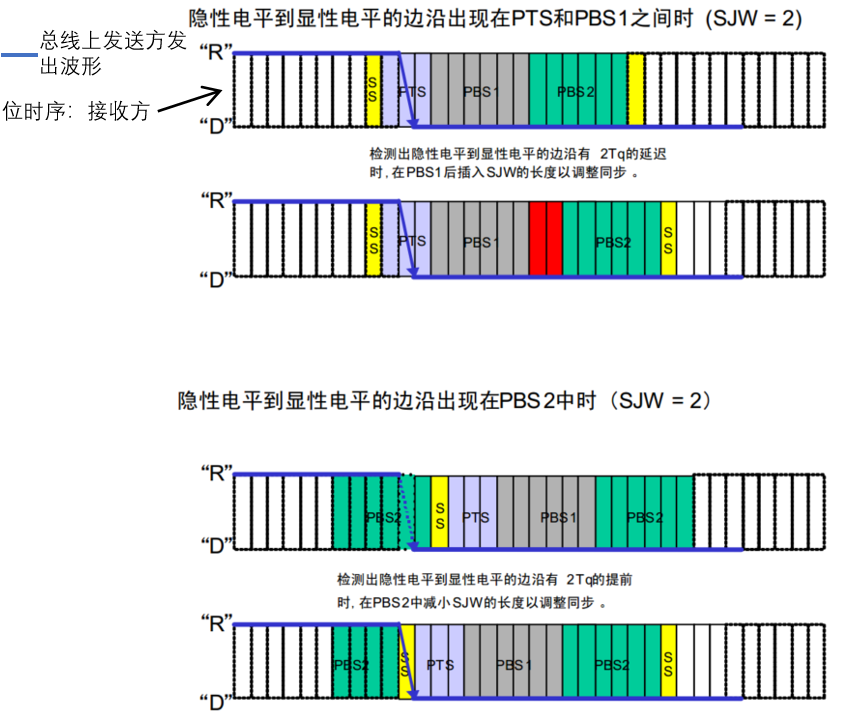
五、CAN总线
目录 一、基础知识 1、can介绍 2、CAN硬件电路 3、CAN电平标准 4、CAN收发器芯片介绍 5、CAN帧格式 ① CAN帧种类 ② CAN数据帧 ③ CAN遥控帧编辑 ④ 位填充 ⑤ 波形实例 6、接收方数据采样 ① 接收方数据采样遇到的问题 ② 位时序 ③ 硬同步 ④ 再同步 ⑤ 波…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
