数字范围按位与

优质博文：IT-BLOG-CN

题目

给你两个整数left和right，表示区间[left, right]，返回此区间内所有数字 按位与 的结果（包含left、right端点）。

示例 1：
输入：left = 5, right = 7
输出：4

示例 2：
输入：left = 0, right = 0
输出：0

示例 3：
输入：left = 1, right = 2147483647
输出：0

0 <= left <= right <= 231 - 1

代码

最直观的解决方案就是迭代范围内的每个数字，依次执行按位与运算，得到最终的结果，但此方法在 [m,n] 范围较大的测试用例中会因超出时间限制而无法通过，因此我们需要另寻他路。

我们观察按位与运算的性质。对于一系列的位，例如 [1,1,0,1,1]，只要有一个零值的位，那么这一系列位的按位与运算结果都将为零。

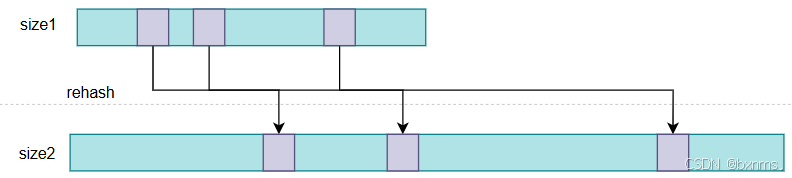
回到本题，首先我们可以对范围内的每个数字用二进制的字符串表示，例如 9=00001001₍₂₎ ，然后我们将每个二进制字符串的位置对齐。

在上图的例子中，我们可以发现，对所有数字执行按位与运算的结果是所有对应二进制字符串的公共前缀再用零补上后面的剩余位。

那么这个规律是否正确呢？我们可以进行简单的证明。假设对于所有这些二进制串，前 i 位均相同，第 i+1 位开始不同，由于 [m,n] 连续，所以第 i+1 位在 [m,n] 的数字范围从小到大列举出来一定是前面全部是 0，后面全部是 1，在上图中对应 [9,11] 均为 0，[12,12] 均为 1。并且一定存在连续的两个数 x 和 x+1，满足 x 的第 i+1 位为 0，后面全为 1，x+1 的第 i+1 位为 1，后面全为 0，对应上图中的例子即为 11 和 12。这种形如 0111… 和 1000… 的二进制串的按位与的结果一定为 0000…，因此第 i+1 位开始的剩余位均为 0，前 i 位由于均相同，因此按位与结果不变。最后的答案即为二进制字符串的公共前缀再用零补上后面的剩余位。

进一步来说，所有这些二进制字符串的公共前缀也即指定范围的起始和结束数字 m 和 n 的公共前缀（即在上面的示例中分别为 9 和 12）。

因此，最终我们可以将问题重新表述为：给定两个整数，我们要找到它们对应的二进制字符串的公共前缀。

方法一：位移

思路

鉴于上述问题的陈述，我们的目的是求出两个给定数字的二进制字符串的公共前缀，这里给出的第一个方法是采用位移操作。

我们的想法是将两个数字不断向右移动，直到数字相等，即数字被缩减为它们的公共前缀。然后，通过将公共前缀向左移动，将零添加到公共前缀的右边以获得最终结果。

算法

如上述所说，算法由两个步骤组成：

我们通过右移，将两个数字压缩为它们的公共前缀。在迭代过程中，我们计算执行的右移操作数。
将得到的公共前缀左移相同的操作数得到结果。

class Solution {public int rangeBitwiseAnd(int m, int n) {int shift = 0;// 找到公共前缀while (m < n) {m >>= 1;n >>= 1;++shift;}return m << shift;}
}

时间复杂度： O(logn)。算法的时间复杂度取决于 m 和 n 的二进制位数，由于 m≤n，因此时间复杂度取决于 n 的二进制位数。
空间复杂度： O(1)。我们只需要常数空间存放若干变量。

方法二：Brian Kernighan 算法

思路与算法

还有一个位移相关的算法叫做「Brian Kernighan 算法」，它用于清除二进制串中最右边的 1。

Brian Kernighan 算法的关键在于我们每次对 number 和 number−1 之间进行按位与运算后，number 中最右边的 1 会被抹去变成 0。

基于上述技巧，我们可以用它来计算两个二进制字符串的公共前缀。

其思想是，对于给定的范围 [m,n]（m<n），我们可以对数字 n 迭代地应用上述技巧，清除最右边的 1，直到它小于或等于 m，此时非公共前缀部分的 1 均被消去。因此最后我们返回 n 即可。

在上图所示的示例（m=9,n=12）中，公共前缀是 00001。在对数字 n 应用 Brian Kernighan 算法后，后面三位都将变为零，最后我们返回 n 即可。

class Solution {public int rangeBitwiseAnd(int m, int n) {while (m < n) {// 抹去最右边的 1n = n & (n - 1);}return n;}
}

时间复杂度： O(logn)。和位移方法类似，算法的时间复杂度取决于 m 和 n 二进制展开的位数。尽管和位移方法具有相同的渐近复杂度，但 Brian Kernighan 的算法需要的迭代次数会更少，因为它跳过了两个数字之间的所有零位。
空间复杂度： O(1)。我们只需要常数空间存放若干变量。