专业学习|动态规划(概念、模型特征、解题步骤及例题)
一、引言
(一)从斐波那契数列引入自底向上算法
(1)知识讲解




(2)matlap实现递归


(3)带有备忘录的遗传算法

(4)matlap实现带有备忘录的递归算法

“;”是为了不显示中间的计算结果;“==”双等号表示判断;“tic、toc”运算开始和结束的时间;

(5)采用自低向上的算法进行求解和代码实现


(二)从斐波那契数列(解决)引入动态规划
(1)从斐波那契数列引入动态规划

(2)动态规划中的常见概念

(3)动态规划解题思路



(4)例题讲解



1)使用递归解决打家劫舍问题

上述使用递归的方法会出现重叠子问题。
2)使用动态规划解决打家劫舍问题

3)动态规划中状态压缩的技巧


5)输出盗窃房屋的编号

(5)动态规划中的最优子结构和无后效性

(6)利用调试功能窥探动态规划函数内部

二、动态规划介绍
(一)动态规划中的常见到的概念

这里我们还是以求解斐波那契数列来举例子,尽管它不算严格的动态规划:
(1)子问题和原问题
原问题就是你要求解的这个问题本身,子问题是和原问题相似但规模较小的问题(原问题本身就是子问题的最复杂的情形,即子问题的特例)。例如:要求F(10),那么求出F(10)就是原问题,求出F(k)(k≤10)都是子问题。
(2)状态
状态就是子问题中会变化的某个量,可以把状态看成我们要求解的问题的自变量。
例如:我们要求的F(10),那么这里的自变量10就是一个状态。
(3)状态转移方程
能够表示状态之间转移关系的方程,一般利用关于状态的某个函数建立起来。例如:F(n)=F(n-1)+ F(n-2),当n为>2的整数时;当n=1或2时,F(n)=1,这种最简单的初始条件一般称为边界条件,也被称为基本方程。
(4)DP数组(DP就是动态规划的缩写)
DP 数组也可以叫"子问题数组",因为 DP 数组中的每一个元素都对应一个子问题的结果,DP数组的下标一般就是该子问题对应的状态。例如:使用自底向上法编程求解时,我们定义的向量FF就可以看成一个DP数组数组下标从1取到n,对应的元素从F(1)取到F(n)。
(二)动态规划建模过程
(1)概述:
建立动态规划的模型,就是分析问题并建立问题的动态规划基本方程。成功地应用动态规划方法的关键,在于识别问题的多阶段特征,将问题分解成为可用递推关系式联系起来的若干子问题,而正确建立基本递推关系方程的关键又在于正确选择状态变量,保证各阶段的状态变量具有递推的状态转移关系.
(2)动态规划模型的建立:
动态规划模型的构成要素:阶段、状态变量、决策变量、状态转移方程以及指标函数,如下图所示

(3)模型建立要点
1.分析题意,识别问题的多阶段特性,按时间或空间的先后顺序适当地划分为满足递推关系的若干阶段,对非时序的静态问题要人为地赋予“时段”概念。
2.正确地选择状态变量,使其具备两个必要特征:
(1)可知性;即过程演变的各阶段状态变量的取值,能直接或间接地确定。
(2)能够确切地描述过程的演变且满足无后效性。即由第k阶段的状态sk出发的后部子过程,可以看作是一个以sk为初始状态的独立过程。
3.根据状态变量与决策变量的含义,正确写出状态转移方程或转移规则。
4.正确列出最优指标函数的递推关系及边界条件(即基本方程)。
(4)动态规划的求解:
动态规划的求解有两种基本方法:逆序解法(后向动态规划方法)、顺序解法(前向动态规划方法)。
逆序解法即寻优的方向与多阶段决策过程的实际行进方向相反,从最后一段开始计算逐段前推,求得全过程的最优策略。与之相反,顺序解法的寻优方向与过程的行进方向相同,计算时从第一段开始逐段向后递推,计算后一阶段要用到前一阶段的求优结果,最后一段计算的结果就是全过程的最优结果。
顺序解法与逆序解法本质上并无区别,一般来说,当初始状态给定时可用逆序解法,当终止状态给定时可用顺序解法。若问题给定了一个初始状态与一个终止状态,则两种方法均可使用。两者的不同之处主要有三点:状态转移方式不同;最优指标函数定义不同;基本方程形式不同。
1)状态转移方式不同

2)指标函数的定义不同

3)基本方程形式不同


(5)动态建模框架


(三)零钱兑换问题讲解(动态规划例题)
(1)零钱兑换问题分析




(2)编程求解

(3)怎样得到具体的硬币组合(分析及matlap实现)


(4)贪心算法解决生活中的找零问题

(5)扩展-背包问题扩展



(四)DP问题分类
| DP 类型 | 介绍 | 解决问题性质 | 解题步骤 | 经典案例 |
|---|---|---|---|---|
| 线性 DP | 针对单串或双串进行状态转移,通常涉及到子序列、子数组的性质。 | 子序列、子数组的优化 | 定义状态,建立递推关系,填写状态表 | 300. 最长上升子序列 <br> 1143. 最长公共子序列 <br> 120. 三角形最小路径和 <br> 53. 最大子序和 <br> 152. 乘积最大子数组 <br> 887. 鸡蛋掉落 <br> 354. 俄罗斯套娃信封问题 <br> 198. 打家劫舍 <br> 213. 打家劫舍 II <br> 股票系列(121, 122, 123, 188, 309, 714) <br> 字符串匹配系列(72, 44, 10) |
| 区间 DP | 通过定义区间状态来求解问题,常用于字符串和序列的性质。 | 区间划分、优化 | 定义区间状态,转移时考虑区间内的所有可能 | 516. 最长回文子序列 <br> 730. 统计不同回文子字符串 <br> 1039. 多边形三角剖分的最低得分 <br> 664. 奇怪的打印机 <br> 312. 戳气球 |
| 背包 DP | 解决选择问题的背包问题,通过状态转移实现选择和价值的最优化。 | 最优选择、容量限制 | 定义物品和背包状态,转移时考虑物品的选择情况 | 416. 分割等和子集 <br> 494. 目标和 <br> 322. 零钱兑换 <br> 518. 零钱兑换 II <br> 474. 一和零 |
| 树形 DP | 针对树形结构进行动态规划,利用树的递归性质。 | 树的路径、子树性质 | 深度优先遍历,维护状态 | 124. 二叉树中的最大路径和 <br> 1245. 树的直径 <br> 543. 二叉树的直径 <br> 333. 最大 BST 子树 <br> 337. 打家劫舍 III |
| 状态压缩 DP | 通过位运算压缩状态,用于处理较大状态空间的情况。 | 状态压缩、子集优化 | 使用位运算表示状态,维护状态转移 | 464. 我能赢吗 <br> 526. 优美的排列 <br> 935. 骑士拨号器 <br> 1349. 参加考试的最大学生数 |
| 数位 DP | 解决涉及数字的组合和计数问题,通常用于约束条件下的数字组合。 | 数字组合、计数 | 定义数字状态,考虑每位的取值和限制 | 233. 数字 1 的个数 <br> 902. 最大为 N 的数字组合 <br> 1015. 可被 K 整除的最小整数 |
| 计数型 DP | 通过计数方法解决路径、组合等问题,结合组合数学原理。 | 路径计数、组合计数 | 定义路径或组合状态,利用数学公式进行转移 | 62. 不同路径 <br> 63. 不同路径 II <br> 96. 不同的二叉搜索树 <br> 1259. 不相交的握手 |
| 递推型 DP | 使用递推关系,通过快速幂等方法提高计算效率。 | 递推关系、状态转移 | 定义递推关系,利用快速幂优化计算 | 70. 爬楼梯 <br> 509. 斐波那契数 <br> 935. 骑士拨号器 <br> 957. N 天后的牢房 <br> 1137. 第 N 个泰波那契数 |
| 概率型 DP | 用于计算概率和期望值,常见于随机过程问题。 | 概率计算、期望值 | 定义状态转移方程,利用概率性质进行推导 | 808. 分汤 <br> 837. 新21点 |
| 博弈型 DP | 涉及两方博弈的问题,通过博弈论原理分析最优策略。 | 策略优化、对抗性游戏 | 定义状态,分析最优选择,通常使用极小化或极大化 | 293. 翻转游戏 <br> 294. 翻转游戏 II <br> 292. Nim 游戏 <br> 877. 石子游戏 <br> 1140. 石子游戏 II <br> 348. 判定井字棋胜负 <br> 794. 有效的井字游戏 <br> 1275. 找出井字棋的获胜者 |
| 记忆化搜索 | 结合深度优先搜索和记忆化技术,适用于状态转移不确定的情况。 | 状态空间优化、DFS | 使用递归和哈希表存储结果,避免重复计算 | 329. 矩阵中的最长递增路径 <br> 576. 出界的路径数 |
参考:力扣上的 DP 问题分类汇总 - 力扣(LeetCode)
三、动态规划——求解多阶段决策过程最优化问题的数学方法
(一)多阶段决策模型及其特点
多阶段决策过程,是指这样的一类特殊的活动过程,问题可以按时间顺序分解成若干相互联系的阶段,在每一个阶段都要做出决策,全部过程的决策是一个决策序列。
根据过程的特性可以将过程按空间、时间等标志分为若干个互相联系又互相区别的阶段。
在每一个阶段都需要做出决策,从而使整个过程达到最好的效果。
各个阶段决策的选取不是任意确定的,它依赖于当前面临的状态,又影响以后的发展。
当各个阶段的决策确定后,就组成了一个决策序列,因而也就决定了整个过程的一条活动路线,这样的一个前后关联具有链状结构的多阶段过程就称为多阶段决策问题。
(二)动态规划求解案例
针对多阶段决策过程的最优化问题,美国数学家Bellman等人在20世纪50年代初提出了著名的最优化原理,把多阶段决策问题转化为一系列单阶段最优化问题,从而逐个求解,创立了解决这类过程优化问题的新方法:动态规划。
对最佳路径(最佳决策过程)所经过的各个阶段,其中每个阶段始点到全过程终点的路径,必定是该阶段始点到全过程终点的一切可能路径中的最佳路径(最优决策),这就是Bellman提出的著名的最优化原理。即 一个最优策略的子策略必然也是最优的。
来源:求解多阶段决策过程最优化问题-CSDN博客

A地到 E 地要铺设一条煤气管道,其中需经过三级中间站,两点之间的连线上的数字表示距离。如图所示,问应该选择什么路线,使总距离最短?
解:整个计算过程分为四个阶段,从最后一个阶段开始。
第四阶段:有两条路。 ①D1E=5,②D2E=2。②最优。

第三阶段:有六条路。
经过C1点——①C1D1+5=8,②C1D2+2=11。
他山之石(参考借鉴)
[1]利用调试功能窥探动态规划函数内部_bilibili
[2]数学建模优化类问题—动态规划_动态规划模型-CSDN博客
[3]【labuladong】动态规划核心套路详解_哔哩哔哩_bilibili
相关文章:

专业学习|动态规划(概念、模型特征、解题步骤及例题)
一、引言 (一)从斐波那契数列引入自底向上算法 (1)知识讲解 (2)matlap实现递归 (3)带有备忘录的遗传算法 (4)matlap实现带有备忘录的递归算法 “࿱…...

数据结构与算法 #时间复杂度 #空间复杂度
文章目录 前言 一、算法的复杂度 二、时间复杂度 三、空间复杂度 四、例题 1、例1:冒泡排序 2、例2: 3、例3: 4、例4: 二分查找 5、例5: 阶乘 6、例6: 斐波那契 五、常见算法复杂度 总结 前言 路漫漫其修远兮,吾将上下而求索&…...

【多机器人轨迹规划最优解问题】
此类应用场景通常很难有严格意义上的最优解,一般只能得到较优解。限制其获得最优解的主要因素如下: 一、问题的复杂性 多机器人系统的高维度性:每台机器人都有自己的位置、速度、任务等多个状态变量,多台机器人组合在一起使得问…...

机器学习及其应用领域【金融领域】
机器学习及其应用领域【金融领域】 一、智能投顾与资产配置二、信贷审批与风险评估三、支付与交易安全四、金融欺诈检测五、市场预测与情绪分析六、客户服务与个性化推荐七、面临的挑战与未来趋势八、总结 一、智能投顾与资产配置 智能投顾:通过机器学习技术&#…...

【实战教程】PHP与七牛云的完美对接,你值得拥有!
前言: 随着互联网的迅速发展,越来越多的网站和应用程序需要处理大量的图片、视频和其他文件。为了有效地存储和管理这些文件,并提供快速的内容分发服务,开发者们常常依赖于云存储和CDN服务提供商。 七牛云是一家领先的云存储和CD…...

2024网易低代码大赛 | 想参赛但不知道搭什么?灵感就这么水灵灵地来了!
9月6日-10月15日,报名进行时!戳我即可报名! 如果你还没想好要开发什么作品来参赛,那就必须往下 我们采访了n位网易内部人士,搜罗了他们的建议,给你多一些灵感! 注意:下文仅为本次比赛…...

(附源码)基于django的电力工程作业现场物资管理系统的设计与实现-计算机毕设 22067
基于django的电力工程作业现场物资管理系统的设计与实现 摘 要 随着电力工程的快速发展,作业现场物资管理成为保障工程进度和质量的关键环节。本文旨在设计并实现一个基于Django框架的电力工程作业现场物资管理系统,以提高物资管理的效率和准确性。该系统…...

数据链路层协议 —— 以太网协议
目录 1.数据链路层解决的问题 2.局域网通信方式 以太网 令牌环网 无线局域网 3.以太网协议 以太网帧格式 对比理解Mac地址和IP地址 认识MTU MTU对IP协议的影响 MTU对UDP的影响 MTU对TCP的影响 基于以太网协议的报文转发流程 交换机的工作原理 4.ARP协议 ARP协议…...

【Javascript】一文看懂JS中的symbol到底是什么东西
作为一名经验丰富的 JavaScript 开发者,你可能对 JavaScript 中的各种数据类型已经了如指掌,比如数字、字符串、布尔值和对象。但是你知道吗?JavaScript 还有一种叫做 Symbol 的类型。在这篇文章里,我们将深入探讨 Symbol 的世界&…...

go语言网络编程
网络编程Go语言网络编程相关APIGo语言网络编程架构Go语言的网络编程实现基于以下几个关键原理:bufiobufio 包的主要功能和使用场景主要类型示例 tcp通信解决粘包粘包和拆包的产生原因解决方法示例 网络编程 Go语言网络编程相关API 1.1 net包net.Listen(network, a…...

LeetcodeLCR 116. 省份数量
文章目录 题目原题链接思路C代码 题目 原题链接 LCR 116. 省份数量 思路 利用并查集的思想,将连接的诚实放在一个集合当中,最后遍历并查集数组判断有几颗树 初始化一个并查集;将连通的城市合并;统计并查集中树的个数;…...
Linux系统上搭建Vulhub靶场
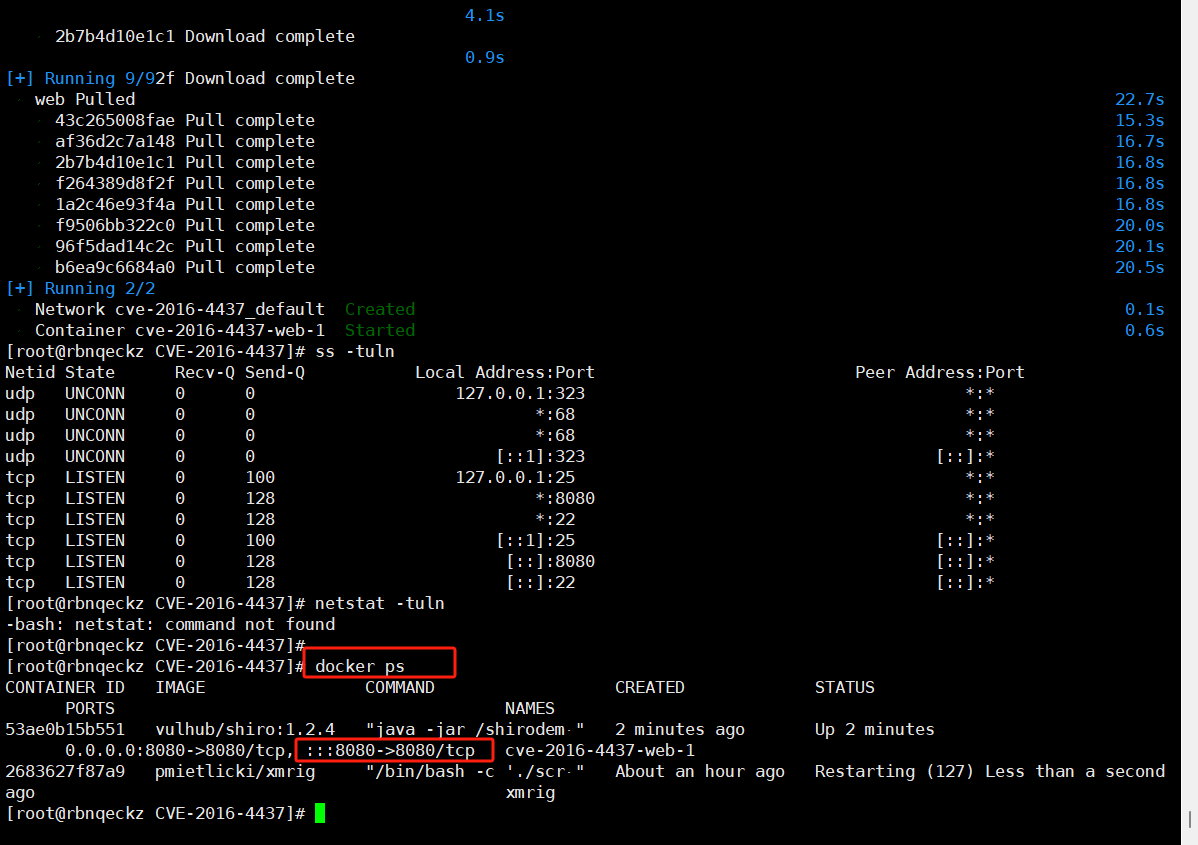
Linux系统上搭建Vulhub靶场 vulhub 是一个开源的漏洞靶场,它提供了各种易受攻击的服务和应用程序,供安全研究人员和学习者测试和练习。要在 Linux 系统上安装和运行 vulhub,可以按照以下步骤进行: 1. 安装 Docker 和 Docke…...

Avalonia的第三方UI库SukiUI详细教程
文章目录 一、SukiUI 简介二、安装与配置1、安装 SukiUI 库:2、配置 Avalonia 项目以使用 SukiUI:三、基本组件使用1、按钮(SukiButton):2、文本框(SukiTextBox):3、标签(SukiLabel):4、下拉列表(SukiComboBox):四、布局与容器1、布局容器介绍:2、使用布局容器组…...

https协议文件上传比http协议慢
一.自己写一个文件上传的接口,在浏览器文件上传https协议比http协议慢(速度上https协议是http协议的八分之一左右),在postman上传是正常的(证明代码是没有问题的),那就是协议的问题 二.经发现&…...

Elasticsearch在大数据处理中的优势
Elasticsearch 在大数据处理中的优势主要体现在以下几个方面: 1. 分布式架构 水平扩展:Elasticsearch 设计为分布式系统,可以轻松地通过增加节点来水平扩展,处理 PB 级别的数据。数据分片和复制:数据自动分片并跨多个…...

cmake--target_compile_definitions
作用 笼统的说是:该命令添加预编译选项到编译目标中。 预编译选项 预编译选项(Preprocessor Options)是一类用于控制 C/C 预处理器行为的编译选项。预处理器是 C/C 编译过程中的第一个处理阶段,主要负责对源代码中的预处理指令…...

MATLAB数据文件读写:1.格式化读写文件
格式化读写文件 matlab提供了对数据文件建立、打开、读取、写入、关闭等操作的函数。 数据文件可以分为两类: 文本文件:以ASCII码形式存储的文本文件;编码基于字符定长,译码相对容易二进制文件:以二进制形式存储的文…...
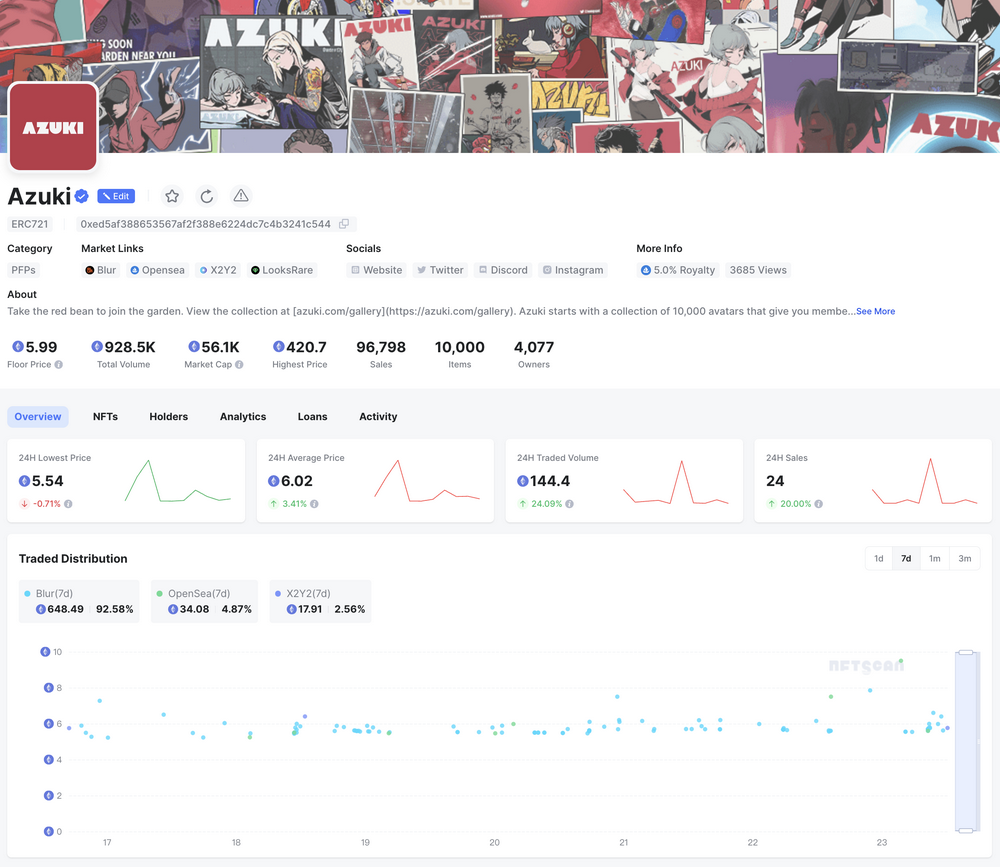
NFTScan | 09.16~09.23 NFT 市场热点汇总
欢迎来到由 NFT 基础设施 NFTScan 出品的 NFT 生态热点事件每周汇总。 周期:2024.09.16~ 2024.09.22 NFT Hot News 01/ DeGods 推出代币 DEGOD,用户可通过 DeGods、y00ts 或 DUST 进行转换 9 月 16 日,Solana NFT 项目 DeGods 推出代币…...
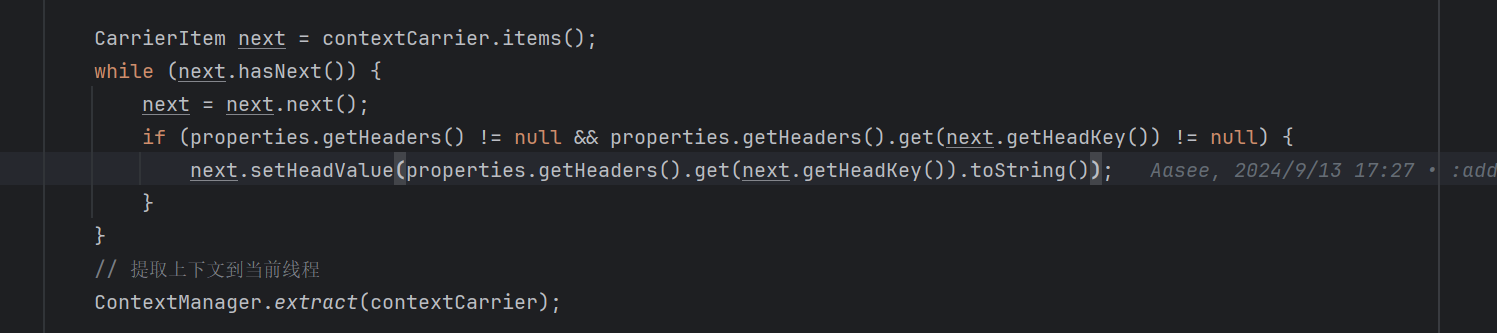
rabbitmq整合skywalking并编写自定义插件增强
rabbitmq整合skywalking 首先先下载准备好skywalking 的服务端和ui控制台,java-agent https://skywalking.apache.org/downloads/ 整合skywalking 我的流程是在生产者和消费者服务中去引入一个mq的sdk,具体SDK的内容可以查看这篇文章 在sdk的pom文件…...

sftp登录ipv6用中括号 `sftp x@[ipv6]`
sftp登录ipv6用中括号 sftp x[ipv6] 实例 sftp root[2::fd40:1:1]SFTP(Secure File Transfer Protocol,安全文件传输协议)是一种基于SSH(Secure Shell)的安全协议,用于在网络上安全地传输文件。当需要登录…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

