数据结构与算法 #时间复杂度 #空间复杂度
文章目录
前言
一、算法的复杂度
二、时间复杂度
三、空间复杂度
四、例题
1、例1:冒泡排序
2、例2:
3、例3:
4、例4: 二分查找
5、例5: 阶乘
6、例6: 斐波那契
五、常见算法复杂度
总结
前言
路漫漫其修远兮,吾将上下而求索;
一、算法的复杂度
当我们编写了一个 算法之后,如何衡量这个算法到底是好还是坏呢?
- 算法在运行的过程中最重要的指标是此算法快不快以及其在运行的过程之中会消耗多少空间,即时间复杂度与空间复杂度;
时间复杂度:衡量一个算法运行的运行快慢
空间复杂度:衡量一个算法运行时所需要的额外空间
注:在早期计算机的发展中,由于计算机的存储容量小,所以比较关注空间复杂度;但是随着计算机行业的快速发展(摩尔定律:每18个月计算机的硬件便会翻一倍),内存越来越大并且越来越便宜,于是现在就不那么关注空间复杂度了;
二、时间复杂度
算法的时间复杂度是一个函数,它定量地描述了该算法的运行时间(该算法执行所消耗的时间);理论来说,时间复杂度是不可能算出来的,只有当此程序在机器上跑起来的时候,才可以知道此算法运行的时间;
注:此处所述的函数,并不是在C语言中的那个函数,而是在数学之中的函数表达式;
时间复杂度为什么不是用来计算该代码运行了多少秒呢?
- 因为并没有一个准确的方式去计算一个算法运行了多少秒;相同的算法在不同的机器上,是有差异的,即一个算法的执行速度受环境的影响;
那么时间复杂度究竟计算的是什么呢?
- 计算的是一个算法之中基本操作(代码)的执行次数;哪个算法的基本操作的执行次数少,那么该算法便会更快;
一个算法花费的时间与其语句的执行次数成正比例,算法中的基本操作的执行次数为算法的时间复杂度;(找到某条基本语句与问题规模N之间的数学表达式)并且在计算的时候也不需要计算该算法精确的执行次数,只需要大概的执行次数便可以了,那么这里便会使用到大O的渐近表示法;
何为大O的渐进表示法?
- 大O符号(Big O notation): 用于描述函数渐进行为的数学符号
推导大O阶方法:
- 用常数1取代运行时间中的所有加法常数
- 在修改后的运行次数函数中,只保留最高阶项;
- 如果最高阶项存在并且不是1,则去除与这个项目相乘的常数(让最高项的系数为1)
最后所得到的结果便是大O阶;
例子代码如下:
void Func1(int N)
{int i = 0;int j = 0;int k = 0;int count = 0;for (i = 0; i < N; i++){for(j = 0; j < N; j++){count++;}}for(k = 0; k < 2 * N; k++){count++;}int M = 10;while (M--){count++;}printf("%d\n", count);
}
倘若要准确地计算上述代码的执行次数 = N^2 + 2*N + M (其中M为10,是一个常数)
根据推导大O阶规则,则会得到该算法的时间复杂度为:O(N^2)

从上例,我们可以得知,大O的渐进表示法去掉了那些对结果影响不大的项,保留了对结果影响最大的项(可以采用数学极限的思想);
计算时间复杂度的技巧:可以大致计算”精确“的,然后再在此基础上利用推导大O阶规则;
另外在有些算法中时间复杂度存在最好、平均、最坏的情况:
最好的情况:任意输入规模的最小运行次数
平均的情况:任意输入规模的期望运行次数
最坏的情况:任意输入规模的最大运行次数
我们在计算一个算法的时间复杂度的时候,一般关注的是其最坏的情况;
三、空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时额外占用存储空间大小的量度;
空间复杂度并不是精确计算这个程序占用了多少byte 的空间,而是采用大O渐进表达式的方式来计算在运行过程中额外运用了多少空间;
注:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器的信息等),在编译期间便已经确定好了,因此空间复杂度主要通过函数在运行的时候显式申请的额外空间来确定的;
换句话说,空间复杂度的计算的是在运行过程中额外占用存储空间的变量个数,倘若在运行的过程中建立栈帧,这也是要算入的;并且遵循推导大O阶的规则;
四、例题
1、例1:冒泡排序

分析:

分析时间、空间复杂度的核心是梳理清楚整个代码的逻辑;
显然冒泡排序的逻辑为:整个冒泡排序会有两个循环,一个控制循环的趟数,一个控制一趟排序之中相邻两元素所要比较的次数,并且每次冒完一趟均会确定好一个元素的最终位置,故而每冒完一趟下一趟冒泡均会减少一次比较;
如此大致看起来,冒泡排序的基本代码执行次数为一个等差数列之和,而复杂度采取的是大O渐进表达式的估算法,即相加的常数项为1,只保留最高项并且最高项的系数为1,显然其时间复杂度变为O(N^2);
而整个冒泡排序的过程都只是在一定大小的数组进行的,并没有使用额外的空间,所以其空间复杂度为O(1);
2、例2:

分析:

注:大O渐进表达式用的未知数用的是N,有时也可以是M、K等字母;
为什么此处的时间复杂度为O(N+M) ?
- 因为在此处N 与 M 均为未知数,并不知道谁大谁小;按照推导大O阶的方式于是乎便得到了O(N+M);
倘若此处有N 与 M 的大小关系,其时间复杂度便会不同:

而对于此算法的空间复杂度,整个算法的执行依靠的是几个变量,并没有使用额外开辟的空间,故而其空间复杂度为O(1);
3、例3:

分析:此算法会受其参数的影响,即参数字符串的长度会影响这个算法完成任务所需要的时间;既然字符串的长度不清楚,便可以将字符串的长度看作为N;
当在一个字符串中查找一个字符额时候,可能一上来便找到了,也有可能在中间位置才找到,亦或许在字符串的结尾才能找到……显然会在字符串的哪个位置找到目标字符这也是未知的;
对于时间复杂度来说,关注的使这个算法最坏的情况,故而此算法的时间复杂度为:O(N) ;
呼应上文所述概念:

平均情况有什么特殊意义?
- 大部分算法并不会看其平均情况,即使看平均情况也是看一下这个算法大概会执行多少次;例如,希尔排序,很少出现最坏的情况,并且最坏的情况难以计算,故而希尔排序这个算法会看其平均情况;(其平均情况的计算会使用到一个非常复杂的数学公式进行计算);
常见的平均情况的计算方式:
1、(最好情况+ 最坏情况)/2
2、按照概率计算(比较复杂)
4、例4: 二分查找

分析:注意二分查找的逻辑;
二分查找会利用到三个指针,一个指向数组的最左,一个指向数组的最右,另外一个指向中间位置;
- 让中间位置的数据与x 相比较,当小于mid 的时候便缩小一半的查找范围,调整left 到mid 右边的位置;倘若大于mid 也会缩小一半的查找范围,调整 right 到 mid 到左边的位置上;而如若mid 所对应得数据等于所要查的数据x ,便代表着查找成功;
显然,我们也不知道所找的数据会在整个数组的哪个位置,存在最好、平均、最坏的情况;二分查找的特性,每次查找没找到便会缩小一半的查找范围,也就是说缩小了几次查找返回便意味着查找了多少次;

最坏的情况就是在这个数组中找不到所找数据,假设我们找了k 次,那么![]() 其中n 为这个数组中元素的个数,由式可得 :
其中n 为这个数组中元素的个数,由式可得 : ![]() ;所以此算法的时间复杂度为:
;所以此算法的时间复杂度为:![]()
当然,由于该二分查找算法并没有使用额外的空间,于是其空间复杂度为:O(1);
有关二分查找的知识补充:
二分查找的查找效率非常高效,但是这个算法是有缺陷的,即必须在有序数组上才能进行查找;倘若面对所要查找的数据是无序的,那么首先就得排序,然而排序也是一个非常消耗的过程;
于是乎便有了后面的 树 --> 二叉树 --> 搜索二叉树 --> 平衡搜索二叉树 --> AVL Tree 、RBTree(红黑树) ,这些算法,无需排序也可以达到二分查找的高效;以及还有更厉害的哈希表、b树系列.[ps:路漫漫……漫漫路……]
5、例5: 阶乘

分析:递归,便会利用到函数栈帧相关知识来理解;
递归中基本代码的执行次数 = 递归次数 * 每次递归中基本代码的执行次数(看每次递归中有无循环);

为什么其空间复杂度为O(N) ?
- 该算法在执行的时候,额外地开辟了空间 -- 函数栈帧的创建;每调用一个函数,便会创建对应的函数栈帧;函数栈帧的开辟个数与递归的次数有关,而在每个函数栈帧中均会使用常数个空间,根据大O渐进表达式的规则,故而其空间复杂度为O(N),图示如下:

递归需要看栈帧的消耗,即看递归的深度;
6、例6: 斐波那契

分析:

显然,斐波那契函数Fib 也遵循: 递归中基本代码的执行次数 = 递归次数 * 每次递归中基本代码的执行次数(看每次递归中有无循环);
如上图所示,Fib 的递归次数为一个等比数列求和并减去一个X(X为假设缺少的常数个递归次数,远小于前面的等比数列求和的所得值)

根据大O渐进表达式,因为(1+X)远小于 2^n, 所以(1+X)可以忽略,故此算法的时间复杂度为: O(2^N);
空间复杂度:
同理,递归的空间复杂度看函数栈帧开辟的次数,即递归的深度 再乘以每次递归中额外使用的空间;Fib 的递归深度以大O渐进表达式为:O(2^N) ; 并且每次递归中并没有使用额外的空间,那么Fib 的空间复杂度便为 O(2^N)?
其实不然,因为 2^N 增长地很快,一般情况在Linux 下,建立一个进程的栈,只有8M ;倘若此算法的空间复杂度为 O(2^N) , 栈肯定会溢出;
实际上,斐波那契函数(递归)是会重复利用空间的,并且不累计;

如上如所示,会先计算一条分支()然后再计算其他分支;即斐波那契函数再创建栈帧的时候会先建立”一支“的栈帧,直到这一支结束便销毁此支创建的函数栈帧……然后再继续调用下一支以实现重复利用空间;那么此时的计算空间复杂度便是看的递归的深度,即最多创建了多少函数栈帧,故而斐波那契函数的空间复杂度为:O(N);
注:递归是一条”支路“递归结束返回了再退回去递归另外一条”支路“;
五、常见算法复杂度
常见算法的时间复杂度包括
- 常数时间复杂度(常数阶): O(1)
- 对数时间复杂度(对数阶): O(log n)
- 线性时间复杂度(线性阶): O(n)
- 线性对数时间复杂度(线性对数阶): O(n log n)
- 平方时间复杂度(平方阶): O(n^2)
- 立方时间复杂度(立方阶): O(n^3)
- 指数时间复杂度(指数阶): O(2^n)

总结
1、时间复杂度与空间复杂度的计算基于大O渐进表达式
2、大O符号(Big O notation): 用于描述函数渐进行为的数学符号
推导大O阶方法:
- 用常数1取代运行时间中的所有加法常数
- 在修改后的运行次数函数中,只保留最高阶项;
- 如果最高阶项存在并且不是1,则去除与这个项目相乘的常数(让最高项的系数为1)
3、分析时间、空间复杂度的核心是梳理清楚整个代码的逻辑;
相关文章:

数据结构与算法 #时间复杂度 #空间复杂度
文章目录 前言 一、算法的复杂度 二、时间复杂度 三、空间复杂度 四、例题 1、例1:冒泡排序 2、例2: 3、例3: 4、例4: 二分查找 5、例5: 阶乘 6、例6: 斐波那契 五、常见算法复杂度 总结 前言 路漫漫其修远兮,吾将上下而求索&…...

【多机器人轨迹规划最优解问题】
此类应用场景通常很难有严格意义上的最优解,一般只能得到较优解。限制其获得最优解的主要因素如下: 一、问题的复杂性 多机器人系统的高维度性:每台机器人都有自己的位置、速度、任务等多个状态变量,多台机器人组合在一起使得问…...

机器学习及其应用领域【金融领域】
机器学习及其应用领域【金融领域】 一、智能投顾与资产配置二、信贷审批与风险评估三、支付与交易安全四、金融欺诈检测五、市场预测与情绪分析六、客户服务与个性化推荐七、面临的挑战与未来趋势八、总结 一、智能投顾与资产配置 智能投顾:通过机器学习技术&#…...

【实战教程】PHP与七牛云的完美对接,你值得拥有!
前言: 随着互联网的迅速发展,越来越多的网站和应用程序需要处理大量的图片、视频和其他文件。为了有效地存储和管理这些文件,并提供快速的内容分发服务,开发者们常常依赖于云存储和CDN服务提供商。 七牛云是一家领先的云存储和CD…...

2024网易低代码大赛 | 想参赛但不知道搭什么?灵感就这么水灵灵地来了!
9月6日-10月15日,报名进行时!戳我即可报名! 如果你还没想好要开发什么作品来参赛,那就必须往下 我们采访了n位网易内部人士,搜罗了他们的建议,给你多一些灵感! 注意:下文仅为本次比赛…...

(附源码)基于django的电力工程作业现场物资管理系统的设计与实现-计算机毕设 22067
基于django的电力工程作业现场物资管理系统的设计与实现 摘 要 随着电力工程的快速发展,作业现场物资管理成为保障工程进度和质量的关键环节。本文旨在设计并实现一个基于Django框架的电力工程作业现场物资管理系统,以提高物资管理的效率和准确性。该系统…...

数据链路层协议 —— 以太网协议
目录 1.数据链路层解决的问题 2.局域网通信方式 以太网 令牌环网 无线局域网 3.以太网协议 以太网帧格式 对比理解Mac地址和IP地址 认识MTU MTU对IP协议的影响 MTU对UDP的影响 MTU对TCP的影响 基于以太网协议的报文转发流程 交换机的工作原理 4.ARP协议 ARP协议…...

【Javascript】一文看懂JS中的symbol到底是什么东西
作为一名经验丰富的 JavaScript 开发者,你可能对 JavaScript 中的各种数据类型已经了如指掌,比如数字、字符串、布尔值和对象。但是你知道吗?JavaScript 还有一种叫做 Symbol 的类型。在这篇文章里,我们将深入探讨 Symbol 的世界&…...

go语言网络编程
网络编程Go语言网络编程相关APIGo语言网络编程架构Go语言的网络编程实现基于以下几个关键原理:bufiobufio 包的主要功能和使用场景主要类型示例 tcp通信解决粘包粘包和拆包的产生原因解决方法示例 网络编程 Go语言网络编程相关API 1.1 net包net.Listen(network, a…...

LeetcodeLCR 116. 省份数量
文章目录 题目原题链接思路C代码 题目 原题链接 LCR 116. 省份数量 思路 利用并查集的思想,将连接的诚实放在一个集合当中,最后遍历并查集数组判断有几颗树 初始化一个并查集;将连通的城市合并;统计并查集中树的个数;…...
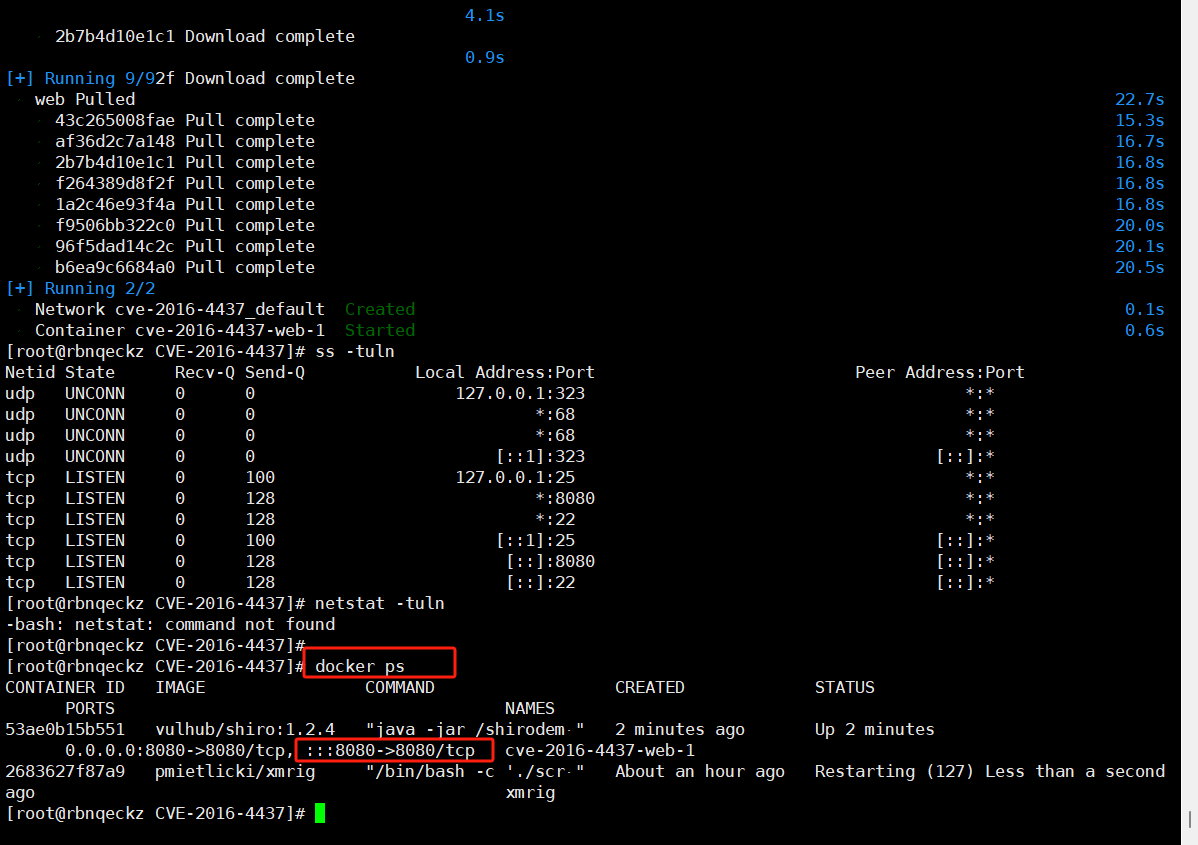
Linux系统上搭建Vulhub靶场
Linux系统上搭建Vulhub靶场 vulhub 是一个开源的漏洞靶场,它提供了各种易受攻击的服务和应用程序,供安全研究人员和学习者测试和练习。要在 Linux 系统上安装和运行 vulhub,可以按照以下步骤进行: 1. 安装 Docker 和 Docke…...

Avalonia的第三方UI库SukiUI详细教程
文章目录 一、SukiUI 简介二、安装与配置1、安装 SukiUI 库:2、配置 Avalonia 项目以使用 SukiUI:三、基本组件使用1、按钮(SukiButton):2、文本框(SukiTextBox):3、标签(SukiLabel):4、下拉列表(SukiComboBox):四、布局与容器1、布局容器介绍:2、使用布局容器组…...

https协议文件上传比http协议慢
一.自己写一个文件上传的接口,在浏览器文件上传https协议比http协议慢(速度上https协议是http协议的八分之一左右),在postman上传是正常的(证明代码是没有问题的),那就是协议的问题 二.经发现&…...

Elasticsearch在大数据处理中的优势
Elasticsearch 在大数据处理中的优势主要体现在以下几个方面: 1. 分布式架构 水平扩展:Elasticsearch 设计为分布式系统,可以轻松地通过增加节点来水平扩展,处理 PB 级别的数据。数据分片和复制:数据自动分片并跨多个…...

cmake--target_compile_definitions
作用 笼统的说是:该命令添加预编译选项到编译目标中。 预编译选项 预编译选项(Preprocessor Options)是一类用于控制 C/C 预处理器行为的编译选项。预处理器是 C/C 编译过程中的第一个处理阶段,主要负责对源代码中的预处理指令…...

MATLAB数据文件读写:1.格式化读写文件
格式化读写文件 matlab提供了对数据文件建立、打开、读取、写入、关闭等操作的函数。 数据文件可以分为两类: 文本文件:以ASCII码形式存储的文本文件;编码基于字符定长,译码相对容易二进制文件:以二进制形式存储的文…...
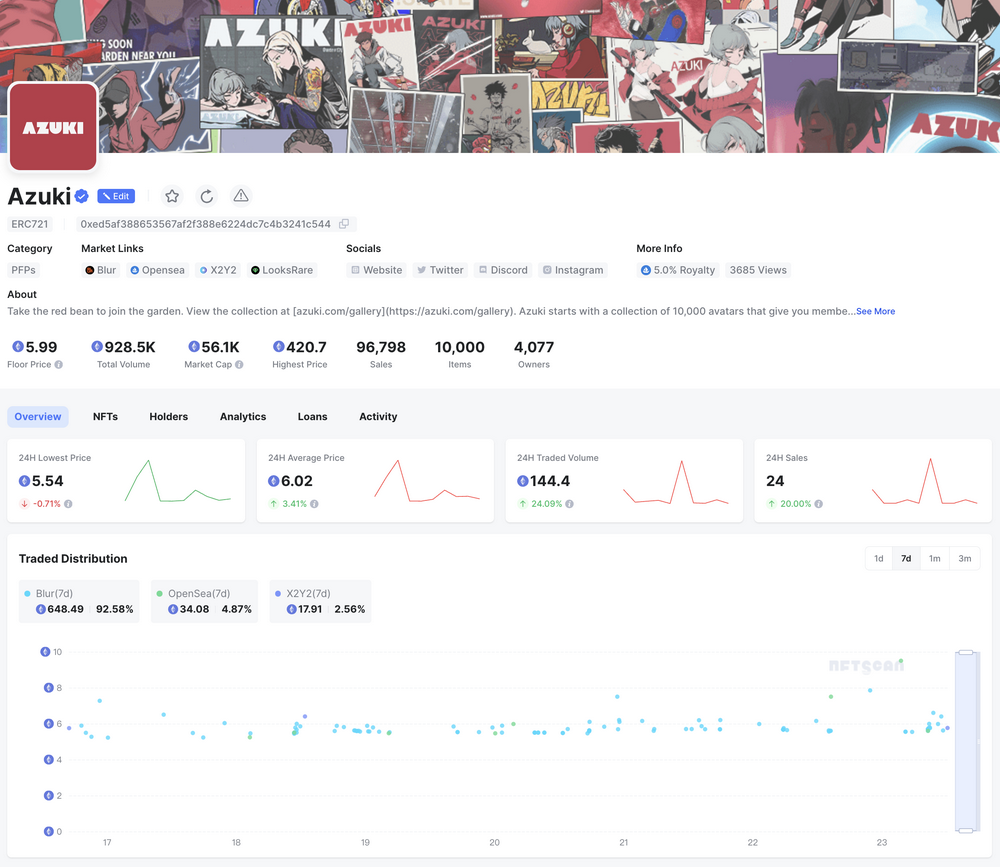
NFTScan | 09.16~09.23 NFT 市场热点汇总
欢迎来到由 NFT 基础设施 NFTScan 出品的 NFT 生态热点事件每周汇总。 周期:2024.09.16~ 2024.09.22 NFT Hot News 01/ DeGods 推出代币 DEGOD,用户可通过 DeGods、y00ts 或 DUST 进行转换 9 月 16 日,Solana NFT 项目 DeGods 推出代币…...
rabbitmq整合skywalking并编写自定义插件增强
rabbitmq整合skywalking 首先先下载准备好skywalking 的服务端和ui控制台,java-agent https://skywalking.apache.org/downloads/ 整合skywalking 我的流程是在生产者和消费者服务中去引入一个mq的sdk,具体SDK的内容可以查看这篇文章 在sdk的pom文件…...

sftp登录ipv6用中括号 `sftp x@[ipv6]`
sftp登录ipv6用中括号 sftp x[ipv6] 实例 sftp root[2::fd40:1:1]SFTP(Secure File Transfer Protocol,安全文件传输协议)是一种基于SSH(Secure Shell)的安全协议,用于在网络上安全地传输文件。当需要登录…...

Python 从入门到实战25(模块)
我们的目标是:通过这一套资料学习下来,通过熟练掌握python基础,然后结合经典实例、实践相结合,使我们完全掌握python,并做到独立完成项目开发的能力。 上篇文章我们讨论了类继承的相关知识。今天我们将学习一下模块的…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
