【每日刷题】Day130
【每日刷题】Day130

🥕个人主页:开敲🍉
🔥所属专栏:每日刷题🍍
🌼文章目录🌼
1. 144. 二叉树的前序遍历 - 力扣(LeetCode)
2. 94. 二叉树的中序遍历 - 力扣(LeetCode)
3. 145. 二叉树的后序遍历 - 力扣(LeetCode)

1. 144. 二叉树的前序遍历 - 力扣(LeetCode)
//思路:非递归。
//递归进行遍历二叉树非常简单,但是非递归就要麻烦很多了。

class Solution {
public:
vector<int> preorderTraversal(TreeNode* root)
{
vector<int> ans;
stack<TreeNode*> st;//存放节点的栈
TreeNode* cur = root;
while(cur||!st.empty())
{
while(cur)//一路往左遍历到空
{
ans.push_back(cur->val);
st.push(cur);
cur = cur->left;
}
TreeNode* tmp = st.top();//获取栈顶节点,也就是返回上一个节点
st.pop();
cur = tmp->right;//去右子树继续重复上述过程
}
return ans;
}
};
2. 94. 二叉树的中序遍历 - 力扣(LeetCode)
//思路:非递归。
//基本思路与 "前序遍历" 的非递归基本一致。唯一的区别在于访问根节点值的时机。
// "前序遍历" 中 cur 在遍历的同时就记录了根节点的值。而中序遍历我们需要在 cur 往左遍历到空后,记录根节点的值。
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root)
{
vector<int> ans;
stack<TreeNode*> st;
TreeNode* cur = root;
while(cur||!st.empty())
{
while(cur)//往左遍历到空,并将节点放入栈中
{
st.push(cur);
cur = cur->left;
}
ans.push_back(st.top()->val);//记录根节点值
TreeNode* tmp = st.top();
st.pop();
cur = tmp->right;
}
return ans;
}
};
3. 145. 二叉树的后序遍历 - 力扣(LeetCode)
//思路:非递归。
//思路大体上还是相同的,但是细节的处理多了很多。
//首先,还是让 cur 往左遍历到空。随后 tmp 获取栈顶元素,此时分为三种情况:
//① 如果 tmp->right 为空,说明此时 tmp 为叶子节点,将值放入 ans 数组中
//② 如果 tmp->right 不为空,说明还有右子树,cur 去到 tmp->right
//③ 这种情况最麻烦:tmp->right 不为空,但是 tmp->right 的节点的值我们已经存储过了,从 tmp->right 回到根节点,此时我们也是需要记录 tmp->val 的。
//但是根据我们①、②点的逻辑是没法做到的,并且会陷入死循环,因为会一直走 cur = tmp->right 的逻辑
//因此这里我们需要用一个变量 prev 来记录存储过的 tmp->right 节点
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root)
{
vector<int> ans;
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* prev = nullptr;
while(cur||!st.empty())
{
while(cur)
{
st.push(cur);
cur = cur->left;
}
TreeNode* tmp = st.top();
//前面思路相同
if(!tmp->right||tmp->right==prev)//如果tmp->right==prev,说明 tmp->right 已经记录过(也可以理解为从tmp->right 回来了),此时 tmp->val也要记录,因为左右子树都遍历完了
{
ans.push_back(tmp->val);
st.pop();
prev = tmp;//使用 prev 记录存储过的 tmp->right
}
else cur = tmp->right;
}
return ans;
}
};
相关文章:

【每日刷题】Day130
【每日刷题】Day130 🥕个人主页:开敲🍉 🔥所属专栏:每日刷题🍍 🌼文章目录🌼 1. 144. 二叉树的前序遍历 - 力扣(LeetCode) 2. 94. 二叉树的中序遍历 - 力扣…...

书生·浦语作业集合
目录: 1. Linux基础知识 2.python基础知识 3.Git基础知识 4.书生大模型全链路开源体系 1.1-Linux基础知识 配置环境后,运行 hello_word.py 在本地终端中进行端口映射 映射成功后,访问 127.0.0.1:7860 1.2-python基础知识 任务…...

得物App科技创新“再上一层楼”,荣获国家级奖项
近日,在2024中国国际服务贸易交易会(简称“服贸会”)上,得物App荣获“科技创新服务示范案例”奖项。这是国家层面对得物App以科技创新保障品质消费、提升消费体验成效的肯定。 在得物App上,90后、95后这些曾经的“新生…...

C#软键盘设计字母数字按键处理相关事件函数
应用场景:便携式设备和检测设备等小型设备经常使用触摸屏来代替键盘鼠标的使用,因此在查询和输入界面的文本或者数字输入控件中使用软件盘来代替真正键盘的输入。 软键盘界面:软键盘界面实质上就是一个普通的窗体上面摆放了很多图片按钮&…...

C++笔记---set和map
1. 序列式容器与关联式容器 前面我们已经接触过STL中的部分容器如:string、vector、list、deque、array、forward_list等,这些容器统称为序列式容器,因为逻辑结构为线性序列的数据结构,两个位置存储的值之间一般没有紧密的关联关…...
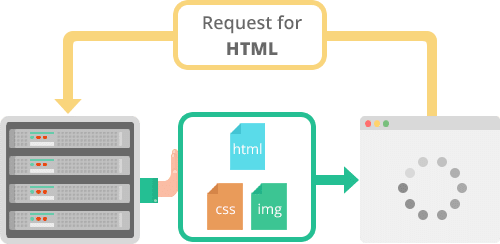
HTTP 教程
HTTP/HTTPS 简介 HTTP(Hypertext Transfer Protocol,超文本传输协议)和 HTTPS(Hypertext Transfer Protocol Secure,超文本传输安全协议)是用于在网络中传输信息的两种主要协议。它们定义了客户端和服务器…...

低代码革命:加速云原生时代的端到端产品创新
随着云计算技术的飞速发展,云原生成为了企业数字化转型的重要方向。云原生技术通过容器化、微服务、持续集成/持续部署(CI/CD)等实践,帮助企业构建和运行可扩展的应用程序。然而,云原生技术的复杂性也给开发团队带来了…...

力扣 92.反转链表Ⅱ
力扣《反转链表》系列文章目录 刷题次序,由易到难,一次刷通!!! 题目题解206. 反转链表反转链表的全部 题解192. 反转链表 II反转链表的指定段24. 两两交换链表中的节点两个一组反转链表 题解225. K 个一组翻转链表K …...
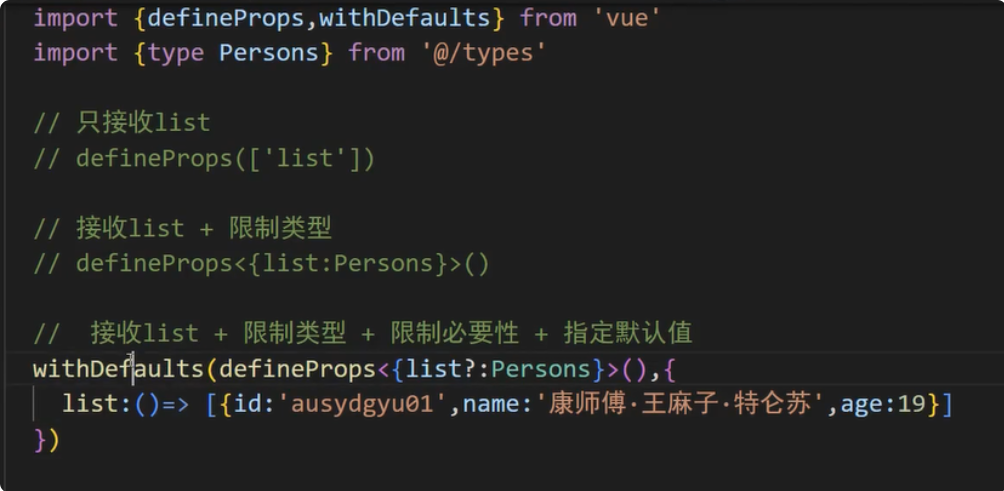
2024年最新版TypeScript学习笔记——泛型、接口、枚举、自定义类型等知识点
今天带来的是来自尚硅谷禹神2024年8月最新的TS课程的学习笔记,不得不说禹神讲的是真的超级棒! 文章目录 TS入门JS中的困扰静态类型检查编译TS命令行编译自动化编译 类型检查变量和函数类型检查字面量类型检查 类型推断类型声明声明对象类型声明函数类型…...

java项目之城镇保障性住房管理系统(源码+文档)
风定落花生,歌声逐流水,大家好我是风歌,混迹在java圈的辛苦码农。今天要和大家聊的是一款基于springboot的城镇保障性住房管理系统。项目源码以及部署相关请联系风歌,文末附上联系信息 。 项目简介: 城镇保障性住房管…...

无人机之航线规划篇
无人机的航线规划是一个复杂但至关重要的过程,它确保了无人机在飞行过程中的安全、高效以及任务的顺利完成。以下是对无人机航线规划的详细解析: 一、定义与目的 无人机航线规划是指依据无人机任务分配,规划出符合安全条件的飞行航线。这一过…...

828 华为云征文|华为 Flexus 云服务器搭建 PicGo 图床
在这个充满非凡意义的日子里,我怀揣着满心的热忱与憧憬,毅然决然地踏上了借助华为 Flexus 云服务器搭建 PicGo 图床的精彩征程。这段旅程,注定充满了无数的挑战与意外之喜,宛如在广袤无垠的数字海洋中勇敢地探寻那神秘而珍贵的宝藏…...

Zabbix 6.4添加中文语言
/usr/share/zabbix/include/locales .inc .phplocale -agrep “zh_CN" yum install langpacks-zh_CN.noarch y y y...

【退役之再次线上部署】Spring Boot + VUE + Nginx + MySQL
这篇博客写在凌晨 4 点 20 分,这个时候我刚线上部署完成 web 项目,自己写的全栈项目 这个点儿,也睡不着了,索性就写篇博客记录一下 一、踩坑实录 这个是 最重要的,所以写在前面 Nginx 配置文件 location location /a…...

Qanything 2 0源码解析系列1:新建知识库
Qanything 2.0源码解析系列1:新建知识库 文章转载自:https://www.feifeixu.top/article/19c76951-5881-4181-bb63-4188b28d3917 😀 前言: qanything所有接口都定义在sanic_api.py中 接口函数定义在同级目录下的handler.py中 新建…...

Redis-01 入门和十大数据类型
Redis支持两种持久化方式:RDB持久化和AOF持久化。 1.RDB持久化是将Redis的数据以快照的形式保存在磁盘上,可以手动触发或通过配置文件设置定时触发。RDB保存的是Redis在某个时间点上的数据快照,可以通过恢复RDB文件来恢复数据。 2.AOF持久化…...

IT行业的现状与未来发展趋势
IT行业的现状与未来发展趋势 近年来,随着科技的迅猛发展,IT行业无疑已经成为全球经济增长的重要驱动力之一。无论是人工智能、大数据,还是云计算和区块链技术,IT行业的创新始终在不断推动着各个领域的变革。 人工智能的广泛应用…...

828华为云征文 | 云服务器Flexus X实例,Docker集成搭建Jenkins CI/CD平台
828华为云征文 | 云服务器Flexus X实例,Docker集成搭建Jenkins CI/CD平台 Jenkins 是一个开源的自动化服务器,用于持续集成(CI)和持续交付(CD)软件项目。它允许开发人员在软件开发过程中自动化各种任务&…...

今日 leetCode 15.三数之和
15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元…...

Games101笔记-二维Transform变换(二)
1、什么是Transform Transform就是通过一个矩阵,进行缩放、旋转、平移等变换 2、缩放、旋转、切变、平移等基础变换 缩放变换: 反射变换: 切变: 绕原点旋转: 以上都是线性变换: 平移变换…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
