LeetCode题练习与总结:二叉树的最近公共祖先--236
一、题目描述
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
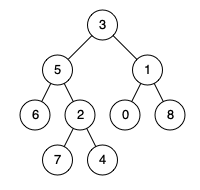
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点5和节点1的最近公共祖先是节点3 。
示例 2:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出:5 解释:节点5和节点4的最近公共祖先是节点5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2 输出:1
提示:
- 树中节点数目在范围
[2, 10^5]内。 -10^9 <= Node.val <= 10^9- 所有
Node.val互不相同。 p != qp和q均存在于给定的二叉树中。
二、解题思路
- 如果当前节点为空,或者当前节点是 p 或 q 中的一个,那么返回当前节点。
- 递归地在左子树中查找 p 和 q 的最近公共祖先。
- 递归地在右子树中查找 p 和 q 的最近公共祖先。
- 如果左子树和右子树中分别找到了 p 和 q,那么当前节点就是最近公共祖先。
- 如果只在左子树中找到了 p 和 q 中的一个或两个,那么最近公共祖先一定在左子树中,返回左子树的查找结果。
- 如果只在右子树中找到了 p 和 q 中的一个或两个,那么最近公共祖先一定在右子树中,返回右子树的查找结果。
三、具体代码
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {// 如果当前节点为空,或者当前节点是 p 或 q,直接返回当前节点if (root == null || root == p || root == q) {return root;}// 递归地在左子树中查找 p 和 q 的最近公共祖先TreeNode left = lowestCommonAncestor(root.left, p, q);// 递归地在右子树中查找 p 和 q 的最近公共祖先TreeNode right = lowestCommonAncestor(root.right, p, q);// 如果左子树和右子树中分别找到了 p 和 q,那么当前节点就是最近公共祖先if (left != null && right != null) {return root;}// 如果只在左子树中找到了 p 和 q,那么最近公共祖先一定在左子树中if (left != null) {return left;}// 如果只在右子树中找到了 p 和 q,那么最近公共祖先一定在右子树中return right;}
}
四、时间复杂度和空间复杂度
1. 时间复杂度
-
单次访问节点:对于树中的每个节点,我们最多只会访问它一次。在递归函数中,每个节点都会被访问一次,然后它的子节点会被递归地访问。
-
递归深度:在最坏的情况下,递归的深度会达到树的高度。在二叉树中,最坏情况是树退化成一条链,此时递归深度为 n(n 是树中节点的数量)。
因此,时间复杂度是 O(n),其中 n 是树中节点的数量。
2. 空间复杂度
-
递归调用栈:由于递归的特性,在递归过程中,函数调用栈会保存每一层递归的信息。在最坏情况下,递归的深度会达到树的高度。
-
递归深度与空间复杂度的关系:在最坏的情况下,如果树是一条链,那么递归的深度就是 n,此时递归调用栈将占用 O(n) 的空间。
因此,空间复杂度是 O(n),其中 n 是树中节点的数量。
综上所述:
- 时间复杂度:O(n),因为每个节点最多被访问一次。
- 空间复杂度:O(n),因为递归调用栈在最坏情况下可能达到 n 的深度。
五、总结知识点
-
递归:
- 递归是一种常用的算法设计方法,它允许函数调用自身来解决问题。
- 在这个代码中,递归用于遍历二叉树并查找两个节点的最近公共祖先。
-
二叉树遍历:
- 代码通过递归实现了二叉树的遍历,具体是后序遍历(先访问左右子节点,再访问根节点)。
- 遍历过程中,如果找到了 p 或 q 节点,则递归函数会返回该节点。
-
逻辑判断:
- 代码包含了多个 if 语句,用于判断递归函数返回的节点是否为空,从而确定最近公共祖先的位置。
-
树的结构:
- 代码操作的数据结构是二叉树,树中的每个节点包含值(val)、左子节点(left)和右子节点(right)。
-
最近公共祖先的定义:
- 代码实现了一个基于最近公共祖先定义的算法,即对于两个节点 p 和 q,找到它们在二叉树中的最低(最深的)共同祖先。
-
边界条件处理:
- 代码首先检查了边界条件,即当前节点是否为空或等于 p 或 q,这确保了递归的基本情况。
-
递归与回溯的结合:
- 在递归过程中,通过回溯(递归返回)的方式,将子树中的信息传递给父节点,以便在父节点做出决策。
以上就是解决这个问题的详细步骤,希望能够为各位提供启发和帮助。
相关文章:

LeetCode题练习与总结:二叉树的最近公共祖先--236
一、题目描述 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也…...

uni-app 多环境配置
前后端分离模式下,不同的环境如开发环境(dev)、测试环境(test)、生产环境(prod)等,不同环境后端数据库、api地址等可能都不同 。 uni-app中只有development和production两个环境 以配…...
【d48】【Java】【力扣】LCR 123. 图书整理 I
思路 方法1:放进list,将list倒置,利用stream,将list改为int类型 方法2:递归:递归通用思路;明确每一层做什么确定返回值确定什么地方接收下层的返回值 每一层:调用下层,然后把自己…...

【MySQL】InnoDB 索引为什么使用B+树而不用跳表?
在MySQL中,为了加速查询,使用B树来构建索引,将查询性能从O(n)优化到O(log n)。虽然跳表同样提供O(log n)的查询效率并且实现相对简单,但B树更适合MySQL的索引使用,原因包括: B树和跳表的区别 B树和跳表的…...

【学习笔记】TLS/SSL握手之Records
TLS / SSL会话是由记录(Records)所组成,有4种records HandshakeAlertChange Cipher SpecApplication DataHandshake和Alert Records被分为子类型(Subtypes): Handshake:Client HelloHandshake&a…...

【MySQL】创建新账号新数据库并授权
在 MySQL 中创建一个名为 new_user 的用户,并设置密码为 new_pass,然后创建一个名为 new_db 的数据库,并将该数据库的所有权限授予 new_user 用户。 登录 MySQL: mysql -u root -p创建用户: CREATE USER new_userlo…...

Nginx反向代理简介,作用及配置;Nginx负载均衡简介,作用及配置;
一,Nginx反向代理 1.1简介 反向代理服务器位于用户与目标服务器之间,但是对于用户而言,反向代理服务器就相当于目标服务器,即用户直接访问反向代理服务器就可以获得目标服务器的资源。同时,用户不需要知道目标服务器的…...

SAP MIGO M7146不支持移动原因
移动类型 Z91 查看配置:Z91 匹配的原因没有921 倒是Z92的原因里面有921 那解决方案有2种,但是要根据具体业务要求来 1、审视一下是否移动原因用错了 ?换一个移动原因 2、确实是这个移动类型 要用到这个移动原因 ,那就在上图 移…...

vue使用PDF.JS踩的坑--部署到服务器上显示pdf.mjs viewer.mjs找不到资源
之前项目使用的pdf.js 是2.15.349版本,最近换了一个4.6.82的版本,在本地上浏览文件运行的好好的,但是发布到服务器(IIS)上打不开文件,控制台提示找不到pdf.mjs viewer.mjs。 之前使用的2.15.349pdf和viewer…...

重型工程车辆数据集
重型工程车辆数据集,内含Bull_dozer(推土机), Dumb_truck(卡车), Excavator(挖掘机), Grader(平地机), Loader(转载机), Mobile_crane(…...
)
【Kubernetes】常见面试题汇总(三十三)
目录 85.简述 kube-proxy 的三种工作模式和原理。 特别说明: 题目 1-68 属于【Kubernetes】的常规概念题,即 “ 汇总(一)~(二十二)” 。 题目 69-113 属于【Kubernetes】的生产应用题。 85.简述 kub…...

ubuntu安装无线网卡驱动(非虚拟机版)
本文不是基于虚拟机,是双系统 太夸张了 实验室居然没网线 只有一个师兄留下来的无线网卡 装完了ubuntu结果没网 make都用不了 然后搜了下大概发现是没有预装gcc和make 参考如下 https://zhuanlan.zhihu.com/p/466440088 https://wwsk.lanzouj.com/iAj4t2ao46zc…...

保障电气安全的电气火灾监控系统主要组成有哪些?
电气火灾是什么? 电气火灾一般是指由于电气线路、用电设备、器具以及供配电设备出现故障性释放的热能:如高温、电弧、电火花以及非故障性释放的能量;如电热器具的炽热表面,在具备燃烧条件下引燃本体或其他可燃物而造成的火灾&…...

gitlab集成CI/CD,shell方式部署
目录 1.首先安装好gitlab和gitlab-runner,这两个,看我以往的教程 2.注册新的 Runner 3. 步骤 3.1 Enter the GitLab instance URL (for example, https://gitlab.com/): 3.2 Enter the registration token: 3.3 Enter a description for the runner: 3…...

UE学习篇ContentExample解读-----------Blueprint_Mouse_Interaction
文章目录 总览描述(Blueprint_Mouse_Interaction)阅览解析1、PlayerControler分析2、拖拽球蓝图分析:3、移动的立方体分析: 新概念总结致谢: 总览描述(Blueprint_Mouse_Interaction) 打开关卡后…...

得物App荣获新奖项,科技创新助力高质量发展
近日,备受瞩目的2024中国国际服务贸易交易会(简称“服贸会”)在北京盛大开幕,这一全球唯一的国家级、国际性、综合型服务贸易盛会再次汇聚了全球服务贸易领域的精英与前沿成果。服贸会由商务部和北京市政府携手打造,并…...
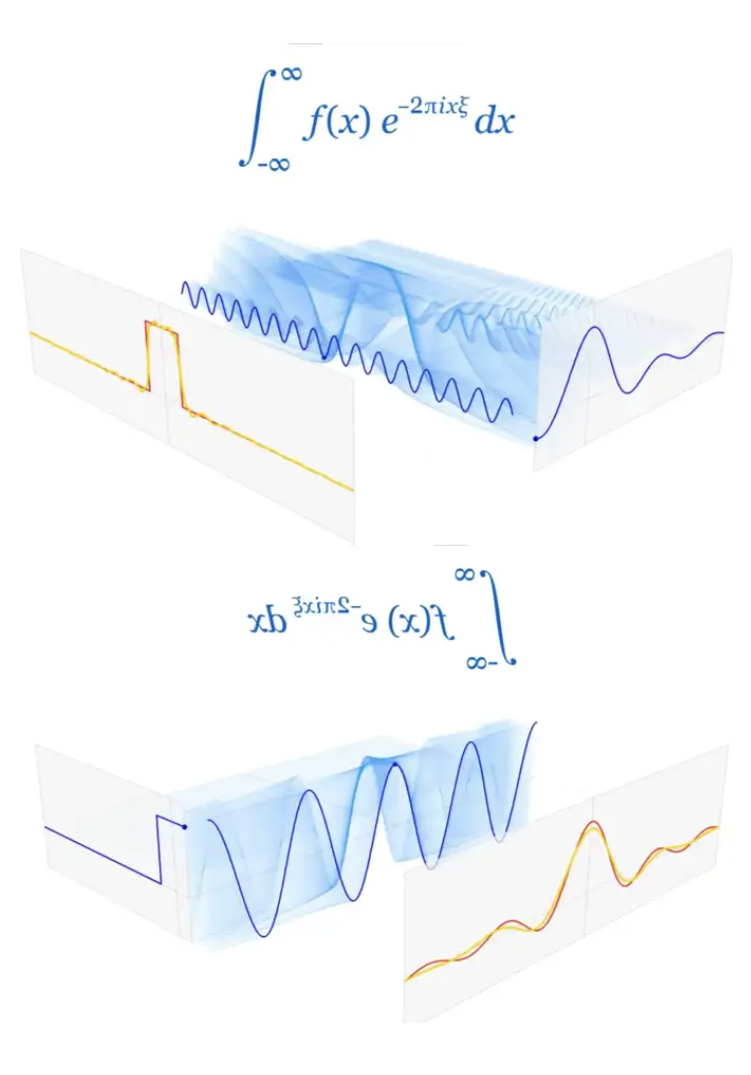
傅里叶变换(对称美)
傅里叶变换(对称美) 冲浪时发现的有趣文章,学习自https://zhuanlan.zhihu.com/p/718139299 摘下来的内容: 傅里叶变换之所以“怪美的嘞”,根本在于它有一种内在的对称性,这一点在上面的图并没有表现出来…...

基于单片机与 PC 机通信的数据采集控制系统设计
摘 要 : 设计出基于单片机与 PC 机通信的数据采集控制系统方法 。 被控对象经传感器 、 电压变换电路 、 A/D 转换芯片与单片机相连, 可将现场参数信息传送至单片机 ; 单片机经继电器驱动控制被控对象运行 。 单片机与 PC 机经电平转换芯片相连, 实现远程通信功能 。…...

MyBatis参数处理
MyBatis 参数处理详解 在 MyBatis 中,参数处理是非常重要的部分,它支持灵活的参数传递方式,以实现与数据库的交互。MyBatis 提供了多种方式来传递参数,包括单个参数、多参数、Java 对象和集合等,这些参数通过 SQL 语句…...
Beyond 5.5旗舰版和高级版激光软件
Beyond 5.5旗舰版和高级版激光软件具有以下一些特点和功能: 1. 强大的功能特性: • 多媒体支持:它是真正的多媒体控制激光软件,除支持基本的激光图案外,还支持视频、3D 动画和绘图程序等,为用户提供了丰富…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
