傅里叶变换（对称美）

傅里叶变换（对称美）

冲浪时发现的有趣文章，学习自https://zhuanlan.zhihu.com/p/718139299

摘下来的内容：

傅里叶变换之所以“怪美的嘞”，根本在于它有一种内在的对称性，这一点在上面的图并没有表现出来。

这种内在的对称性是什么呢？可以理解为：

频谱是时域信号在一个​**希尔伯特空间​中的连续正交归一基下展开的展开系数，于此同时，时域信号也是频谱在相同形式的希尔伯特空间中的连续正交归一基下的展开的展开系数。**

​​

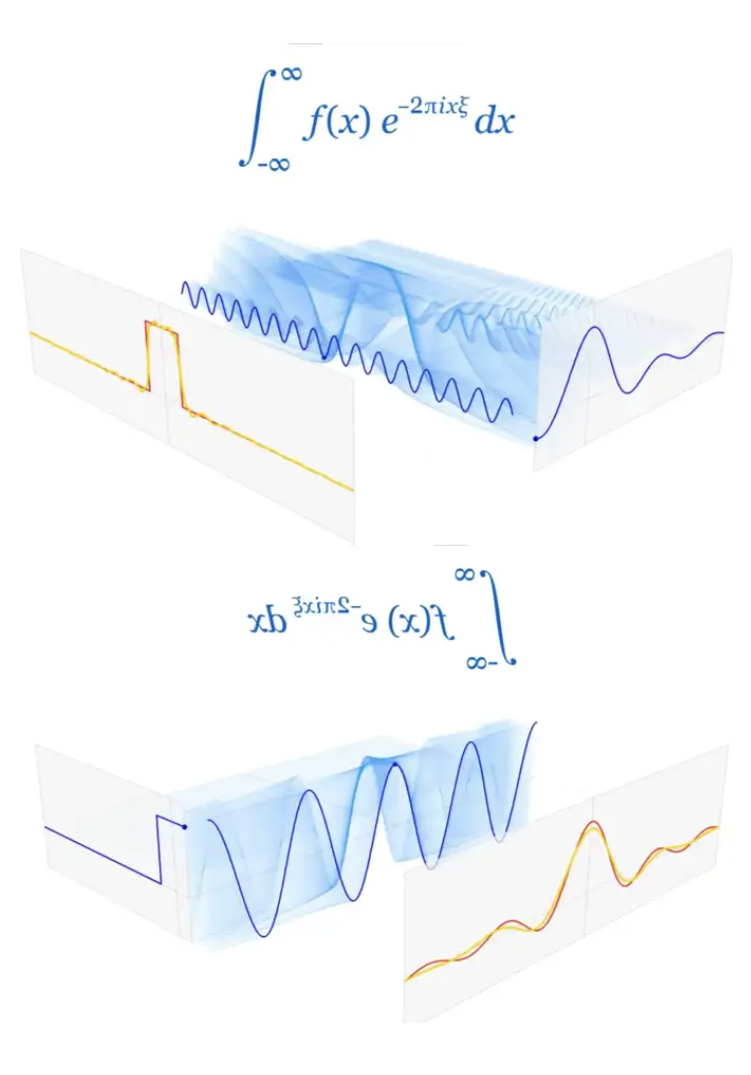
比较直观的视频：https://www.youtube.com/watch?v=r4c9ojz6hJg&ab_channel=SimonXu

以前比较少关注这种对称的方式，也很少有这种连续的视频图，也能从一个侧面去了解傅里叶变换，这篇文章主要是着重对称性这个点，也算是加深一下自己的理解。写得很好。

文章二：https://zhuanlan.zhihu.com/p/40396861

为了“简单”而进行“分解”，为了更好的“分解”，人类又发明了“正交”的概念。何谓正交呢，它其实脱胎于“垂直”而又有更丰富的内涵。我们知道在垂直坐标系中，三个坐标轴的相互垂直的，这样的好处是各个轴向之间是独立的，互不干扰的。当然，这些描述都是定性的，对于严谨的数学家和工程师而言，这是不可接受的。于是，又有一个新的概念引入了:“内积”，当内积为零的时候，两个量就是正交的。

整理一下我们的思路：我们想要“简单”，要进行“分解”，想要更好的“分解”，要进行“正交化”，想要定量描述“正交化”，规定“内积”为零为“正交”。总的逻辑是这样的：简单→分解→正交→内积。

说了这么多，这和傅里叶分析有什么关系？现在我要告诉大家：傅里叶分析就是进行“正交分解”，不理解细节没关系，领会到了这个概念，就理解一半了。为了严谨（实际上很不严谨^_^），我们需要将逻辑关系反过来，先从内积说起。

在三维直角坐标系里面，任何一个坐标轴的方向上长度为$1$ 的向量称之为一个基，相互垂直的基称之为正交基：$（1,0,0）$ 代表$x$ 轴的基，$（0,1,0）$ 代表

$y$ 轴的基，$（0,0,1）$代表$z$ 轴的基。假设 $\bar{x}=（a_1,b_1,c_1）$,$\bar{y}=(a_2,b_2,c_2)$ ，规定内积为：
$\bar{y}=(a_2,b_2,c_2)$ ，

规定内积为：

$<\bar{x},\bar{y}>=<(a_1,b_1,c_1),(a_2,b_2,c_2)>=a_1{a}_2+b_1{b}_2+c_1{c}_2$

一个很简单的结论：$<(1,0,0),(0,1,0)>=1\times 0+0\times 1+0\times 0=0$,说明任意两个基确实是正交的。

$<(1,0,0),(1,0,0)>=1\times 1+0\times 0+0\times 0=1$ ，说明向量与自己的内积是一个常数。那如何表示任意一个向量呢？比如$v=（5,2,7）$在线性代数里面，我们是这么做的：

$A=<v,x>=<(5,2,7),(1,0,0)>=5$ （1）

$B=<v,y>=<(5,2,7),(0,1,0)>=2$ （2）

$C=<v,z>=<(5,2,7),(0,0,1>=7$ （3）

于是，$v=Ax+By+Cz$ ，相信得出以下结论是很容易的：内积相当于一种“投影”操作，任意向量与基之间的内积就是该向量在基所在方向的投影，内积的结果就是系数。

假如基不再是一个向量，而是一个函数，会有什么结果？

$e^{i\omega t}$ 在这种内积的定义下是一族正交基，更深刻的数学知识可以证明，在一定条件下，它不仅是正交的，还是完备的，也就是说，只要满足一定的条件，任何函数都可以用$e^{i\omega t}$ 叠加出来。

$$f(t)=\sum _{\omega =-\infty }^{+\infty }{A}_{\omega }{e}^{i\omega t}=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }F(\omega )e^{i\omega t}d\omega$$

‍

这个式子的含义为：在一定条件下，任意函数（$f(t)$ ）都可以由完的正交基​$e^{i\omega t}$ 叠加而成，每个正交基对应的系数为$F(\omega )$ 。（$1/2\pi$ 的引入是为了计算方便，傅里叶变换有多种形式，也有不带$1/2\pi$ ，这里采用了最通用的形式）。

$F(\omega )$ 。（$1/2\pi$ 的引入是为了计算方便，傅里叶变换有多种形式，也有不带$1/2\pi$ ，这里采用了最通用的形式）。

系数$F(\omega )$ 可以由内积计算而来：

$$F(\omega )=<f(t),e^{i\omega t}>={\int }_{-\infty }^{+\infty }f(t)e^{-i\omega t}dt$$

因此，傅里叶变换的本质可以看成是正交分解：$f(t)$ 和$e^{i\omega t}$ 求内积的时候，$f(t)$ 中只有频率为$\omega$ 的分量才会有内积的结果，其余分量的内积为0，积分值是时间从负无穷到正无穷，可以看成是$f(t)$ 整个信号在$e^{i\omega t}$ 上的投影，只要给定一个频率$\omega$ ，都会对应一个系数$F(\omega )$ 来。

这个结论倒是与之前看到的保持一致，傅里叶变换的本质是正交分解。

$f(t)$ 中只有频率为$\omega$ 的分量才会有内积的结果，其余分量的内积为0，积分值是时间从负无穷到正无穷，可以看成是$f(t)$ 整个信号在$e^{i\omega t}$ 上的投影，只要给定一个频率$\omega$ ，都会对应一个系数$F(\omega )$ 来。

$\omega$ ，都会对应一个系数$F(\omega )$ 来。

‍