Offer60:n个骰子的点数
题目:把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。
分析:要解决这个问题,我们需要先统计出每个点数出现的次数,然后把每个点数出现的次数除以,就能求出每个点数出现的概率了。我们可以用两个数组来存储骰子点数的每个总数出现的次数。在一轮循环中,第一个数组中的第n个数字表示骰子和为n出现的次数,在下一轮循环中,我们加上一个新的骰子,此时和为n的骰子出现的次数应该等于上一轮循环中骰子点数和为n-1、n-2、n-3、n-4、n-5、n-6的次数的总和。
代码:用两个数组模拟骰子投掷过程
const int g_maxValue = 6; //骰子的最大点数 全局常量
void PrintProbability(int number){ //number为骰子的个数if(number < 1)return;int* pProbability[2];pProbability[0] = new int[g_maxValue * number + 1]; //掷骰子得到的点数范围是1~number*最大点数pProbability[1] = new int[g_maxValue * number + 1];for(int i = 0;i < g_maxValue * number + 1; ++i){ //数组初始化pProbability[0][i] = 0;pProbability[1][i] = 0;}int flag = 0; //flag用于交换两个数组for(int i = 1;i <= g_maxValue;++i){ //第一个骰子得到的点数范围是1~骰子的最大点数,次数为1pProbability[flag][i] = 1;}for(int k = 2;k <= number; ++k){ //第二个骰子到第number个骰子for(int i = 0;i < k; ++i){pProbability[1 - flag][i] = 0; //初始化投到第k个骰子不会再出现的点数和为0}for(int i = k;i <= g_maxValue * k;++i){ //第k个骰子投出的点数范围是k~k * 骰子最大点数pProbability[1 - flag][i] = 0;for(int j = 1;j <= i && j <= g_maxValue;++j){ //当前骰子的点数为i,获得这个点数的次数为上一次掷骰子得到点数i - j的次数,j的范围为1~骰子的最大点数,然后将所有的次数相加pProbability[1 - flag][i] += pProbability[flag][i - j];}}flag = 1 - flag;}double total = pow((double)g_maxValue,number); //所有点数的总次数for(int i = number;i <= g_maxValue * number;++i){double ratio = (double)pProbability[flag][i] / total; //当前点数的概率printf("%d:%e\n",i,ratio);}delete[] pProbability[0]; delete[] pProbability[1];
}相关文章:
Offer60:n个骰子的点数
题目:把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。 分析:要解决这个问题,我们需要先统计出每个点数出现的次数,然后把每个点数出现的次数除以,就能求出每个点数出现的概率了。我们…...

几种常见的索引类型扫描
第一种:index unique scan 索引唯一扫描,当可以优化器发现某个查询条件可以利用到主键、唯一键、具有外键约束的列,或者只是访问其中某行索引所在的数据的时候,优化器会选择这种扫描类型。第二种:index range scan 索…...

苹果CMS插件:优化蜘蛛访问内容,提升百度收录率
确保蜘蛛抓取原始内容 专为苹果CMS设计的广告管理插件,能够智能识别搜索引擎蜘蛛与普通访客,确保蜘蛛访问时展示原始内容,从而提升被百度等搜索引擎收录的几率。 广告显示提升收益 对于普通访客,该插件则优先显示广告内容&#…...

后端开发刷题 | 没有重复项数字的全排列
描述 给出一组数字,返回该组数字的所有排列 例如: [1,2,3]的所有排列如下 [1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2], [3,2,1]. (以数字在数组中的位置靠前为优先级,按字典序排列输出。) 数据范围:数字…...

Python中的“打开与关闭文件”:从入门到精通
引言 在日常生活中,我们经常会遇到需要读取或保存信息的情况,比如记录笔记、保存配置信息或者处理大量的数据文件等。对于程序员来说,如何高效、安全地管理这些信息显得尤为重要。Python中的文件操作功能强大且易于使用,可以帮助…...
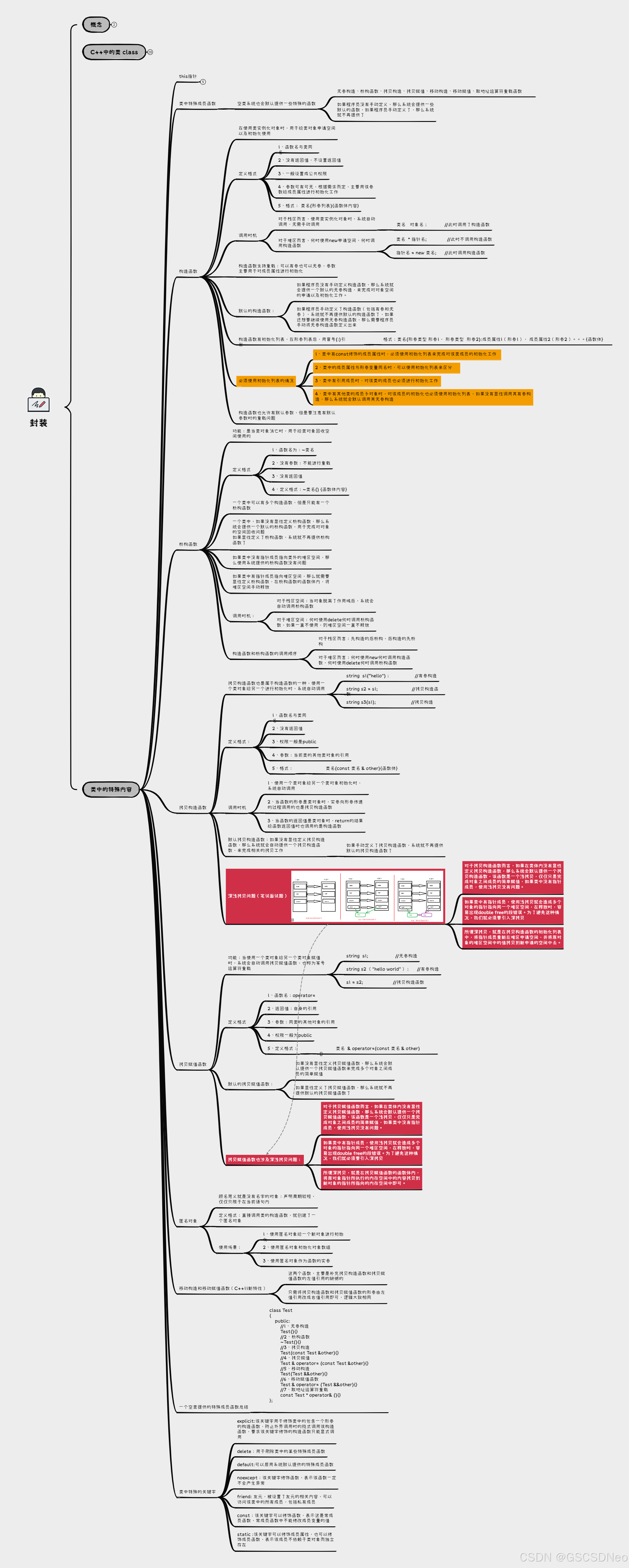
9.23 My_string.cpp
my_string.h #ifndef MY_STRING_H #define MY_STRING_H#include <iostream> #include <cstring>using namespace std;class My_string { private:char *ptr; //指向字符数组的指针int size; //字符串的最大容量int len; //字符串当前…...

【android10】【binder】【3.向servicemanager注册服务】
系列文章目录 可跳转到下面链接查看下表所有内容https://blog.csdn.net/handsomethefirst/article/details/138226266?spm1001.2014.3001.5501文章浏览阅读2次。系列文章大全https://blog.csdn.net/handsomethefirst/article/details/138226266?spm1001.2014.3001.5501 目录 …...
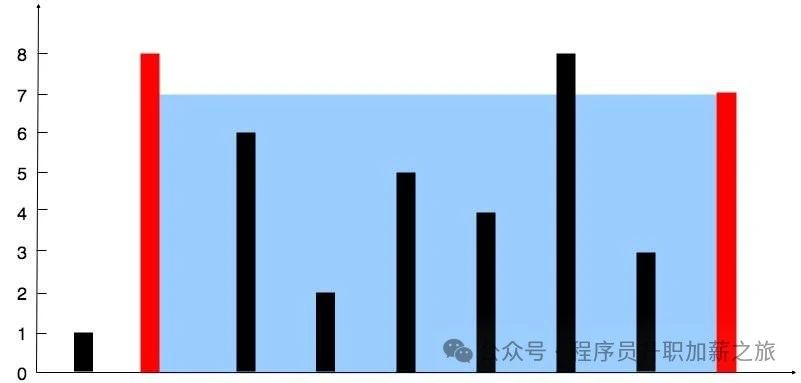
Java — LeetCode 面试经典150题(一)
双指针 125.验证回文串 题目 如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。 字母和数字都属于字母数字字符。 给你一个字符串 s,如果它是 回文串 ,返回…...

Python酷玩之旅_mysql-connector
前言 Python作为数据科学、机器学习等领域的必选武器,备受各界人士的喜爱。当你面对不同类型、存储于各类介质的数据时,第一时间是不是要让它亮个相?做个统计,画个图表,搞个报表… 等等。 正如Java中的JdbcDriver一样…...
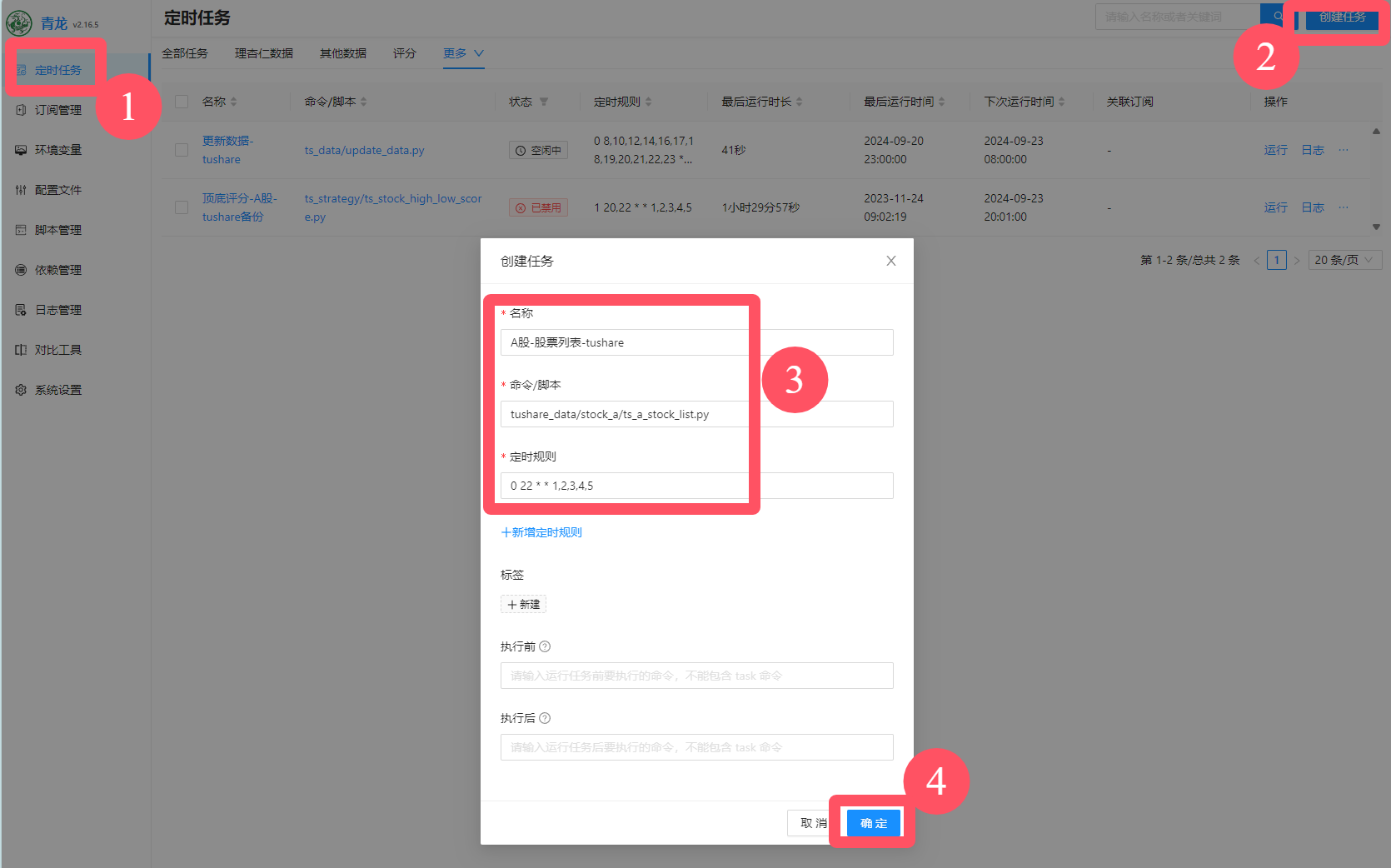
7.搭建个人金融数据库之快速获取股票列表和基本信息!
前边我们提过,免费的数据一般来自于爬虫,获取难度和维护成本都比较高,其实不太适合小白用户。所以非必要情况下,我们尽量不用这种方式来获取数据。 我自己用的比较多的是tushare,一般来说有它也就够了,大…...
Nginx基础详解1(单体部署与集群部署、负载均衡、正反代理、nginx安装)
本阶段的任务 1.学会集群的操作概念 2.完成对Nginx的入门操作 3.使用Nginx实现集群和负载均衡 4.使用Nginx实现高可用的方案 目录 1.单体部署与集群部署 1.1单体部署的概念 1.2单体部署的优缺点 1.3集群部署的概念 1.4集群部署的优缺点 1.5集群部署需要注意的点 1.…...

等保一体机如何帮你应对网络攻击
等保一体机如何帮你应对网络攻击 在当今信息化时代,网络安全已成为企业和组织面临的重要挑战。随着网络攻击手段的不断升级,传统的安全防护措施已难以应对复杂多变的威胁。等保一体机作为一种集成化的安全防护解决方案,能够有效帮助企业应对…...
CVE-2024-1112 Resource Hacker 缓冲区溢出分析
漏洞简述 CVE-2024-1112 是 Resource Hacker 软件的一个缓冲区溢出漏洞。该漏洞存在于版本 3.6.0.92 中。由于软件在处理命令行中的文件路径时未对文件字符串长度进行限制,过长的字符串参数导致内存被过度写入,从而引发缓冲区溢出。 漏洞复现 构造长度…...

WebGL渲染与创建2D内容
目录 创建画布2D渲染修改顶点着色器光照深度测试混合模式WebGL是一个强大的工具,可以用来在Web浏览器中创建复杂的3D图形。虽然它的设计初衷是为了3D渲染,但也可以用于创建2D内容。通过巧妙地利用几何、投影和纹理,我们可以构建出各种2D图形。 创建画布 首先,我们需要在H…...
ArcGIS Desktop使用入门(三)图层右键工具——拓扑(下篇:地理数据库拓扑)
系列文章目录 ArcGIS Desktop使用入门(一)软件初认识 ArcGIS Desktop使用入门(二)常用工具条——标准工具 ArcGIS Desktop使用入门(二)常用工具条——编辑器 ArcGIS Desktop使用入门(二&#x…...
LeetCode题练习与总结:二叉树的最近公共祖先--236
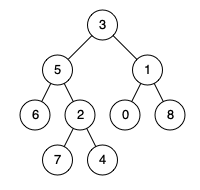
一、题目描述 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也…...

uni-app 多环境配置
前后端分离模式下,不同的环境如开发环境(dev)、测试环境(test)、生产环境(prod)等,不同环境后端数据库、api地址等可能都不同 。 uni-app中只有development和production两个环境 以配…...
【d48】【Java】【力扣】LCR 123. 图书整理 I
思路 方法1:放进list,将list倒置,利用stream,将list改为int类型 方法2:递归:递归通用思路;明确每一层做什么确定返回值确定什么地方接收下层的返回值 每一层:调用下层,然后把自己…...

【MySQL】InnoDB 索引为什么使用B+树而不用跳表?
在MySQL中,为了加速查询,使用B树来构建索引,将查询性能从O(n)优化到O(log n)。虽然跳表同样提供O(log n)的查询效率并且实现相对简单,但B树更适合MySQL的索引使用,原因包括: B树和跳表的区别 B树和跳表的…...

【学习笔记】TLS/SSL握手之Records
TLS / SSL会话是由记录(Records)所组成,有4种records HandshakeAlertChange Cipher SpecApplication DataHandshake和Alert Records被分为子类型(Subtypes): Handshake:Client HelloHandshake&a…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
