【力扣周赛 338】
6354. K 件物品的最大和 - 力扣(Leetcode)
袋子中装有一些物品,每个物品上都标记着数字 1 、0 或 -1 。
给你四个非负整数 numOnes 、numZeros 、numNegOnes 和 k 。
袋子最初包含:
numOnes 件标记为 1 的物品。
numZeroes 件标记为 0 的物品。
numNegOnes 件标记为 -1 的物品。
现计划从这些物品中恰好选出 k 件物品。返回所有可行方案中,物品上所标记数字之和的最大值。
示例 1:
输入:numOnes = 3, numZeros = 2, numNegOnes = 0, k = 2 输出:2 解释:袋子中的物品分别标记为 {1, 1, 1, 0, 0} 。取 2 件标记为 1 的物品,得到的数字之和为 2 。 可以证明 2 是所有可行方案中的最大值。
示例 2:
输入:numOnes = 3, numZeros = 2, numNegOnes = 0, k = 4 输出:3 解释:袋子中的物品分别标记为 {1, 1, 1, 0, 0} 。取 3 件标记为 1 的物品,1 件标记为 0 的物品,得到的数字之和为 3 。 可以证明 3 是所有可行方案中的最大值。
提示:
0 <= numOnes, numZeros, numNegOnes <= 50
0 <= k <= numOnes + numZeros + numNegOnes
思路
easy等级的,比较简单。
要去到最大值,分别有以下3种情况:
全部是1
1和0混合
1、0和-1混合,因为 k <= numOnes + numZeros + numNegOnes,所以最后的值就是 1的个数减去我们需要的-1的个数(k - numOnes - numZeros)
代码实现
class Solution {public int kItemsWithMaximumSum(int numOnes, int numZeros, int numNegOnes, int k) {if(numOnes > k){return k;}else if(numOnes + numZeros > k){return numOnes;}else{return numOnes - k + numOnes + numZeros;}}
}6355. 质数减法运算 - 力扣(Leetcode)
给你一个下标从 0 开始的整数数组 nums ,数组长度为 n 。
你可以执行无限次下述运算:
选择一个之前未选过的下标 i ,并选择一个 严格小于 nums[i] 的质数 p ,从 nums[i] 中减去 p 。
如果你能通过上述运算使得 nums 成为严格递增数组,则返回 true ;否则返回 false 。
严格递增数组 中的每个元素都严格大于其前面的元素。
示例 1:
输入:nums = [4,9,6,10] 输出:true 解释: 在第一次运算中:选择 i = 0 和 p = 3 ,然后从 nums[0] 减去 3 ,nums 变为 [1,9,6,10] 。 在第二次运算中:选择 i = 1 和 p = 7 ,然后从 nums[1] 减去 7 ,nums 变为 [1,2,6,10] 。 第二次运算后,nums 按严格递增顺序排序,因此答案为 true 。
示例 2:
输入:nums = [6,8,11,12] 输出:true 解释:nums 从一开始就按严格递增顺序排序,因此不需要执行任何运算。
示例 3:
输入:nums = [5,8,3] 输出:false 解释:可以证明,执行运算无法使 nums 按严格递增顺序排序,因此答案是 false 。
提示:
1 <= nums.length <= 1000
1 <= nums[i] <= 1000
nums.length == n
思路
首先,说一下踩到的坑。
严格小于 nums[i] 的质数 p。严格小于就是不包括等于,应该是 a < b,而不是 a <= b
每一个位置减去最佳的数(p)之后,记得break,跳出寻找最佳的数的循环。
然后就是这一题的思路。一看到这个题目,不知道怎么去找到每个位置最合适的p,因为后面的数,会因为前面的数受影响,而后面又注意到“选择一个之前未选过的下标 i”,所以每一个位置只可以减一次。所以我们就从头开始遍历,前面的变成最小的能够变成的数,如果还是不能变成严格递增的序列,那么这个序列不可能会变成严格递增的序列。
代码实现
class Solution {public static boolean isPrime(int n) { //判断质数(素数)if (n <= 3) {return n > 1;}//判断一个数能否被小于sqrt(n)的数整除int sqrt = (int)Math.sqrt(n);for (int i = 2; i <= sqrt; i++) {if(n % i == 0) {return false;}}return true;}public boolean check(int[] nums, int k){ //判断该序列是否严格递增int flag = 0;for(int i = k; i < nums.length - 1; i++){if(nums[i] >= nums[i + 1]){flag = 1;break;}}if(flag == 0){return true;}return false;}public void find(int[] nums, int k){ //找到最合适的pif(k == 0){ //序列第一位不受前面一位的影响,因为没有前面一位if(nums[k] > 2){for(int j = nums[k] - 1; j > 1; j--){if(isPrime(j)){nums[k] = nums[k] - j;break;}}}}else{for(int j = nums[k] - 1; j > 1; j--){if(isPrime(j) && nums[k] - j > nums[k - 1]){nums[k] = nums[k] - j;break;}}}}public boolean primeSubOperation(int[] nums) {if(check(nums, 0)){return true;}for(int i = 0; i < nums.length; i++){find(nums, i);if(check(nums, 0)){return true;}}return false;}
}6357. 使数组元素全部相等的最少操作次数 - 力扣(Leetcode)
给你一个正整数数组 nums 。
同时给你一个长度为 m 的整数数组 queries 。第 i 个查询中,你需要将 nums 中所有元素变成 queries[i] 。你可以执行以下操作 任意 次:
将数组里一个元素 增大 或者 减小 1 。
请你返回一个长度为 m 的数组 answer ,其中 answer[i]是将 nums 中所有元素变成 queries[i] 的 最少 操作次数。
注意,每次查询后,数组变回最开始的值。
示例 1:
输入:nums = [3,1,6,8], queries = [1,5] 输出:[14,10] 解释:第一个查询,我们可以执行以下操作: - 将 nums[0] 减小 2 次,nums = [1,1,6,8] 。 - 将 nums[2] 减小 5 次,nums = [1,1,1,8] 。 - 将 nums[3] 减小 7 次,nums = [1,1,1,1] 。 第一个查询的总操作次数为 2 + 5 + 7 = 14 。 第二个查询,我们可以执行以下操作: - 将 nums[0] 增大 2 次,nums = [5,1,6,8] 。 - 将 nums[1] 增大 4 次,nums = [5,5,6,8] 。 - 将 nums[2] 减小 1 次,nums = [5,5,5,8] 。 - 将 nums[3] 减小 3 次,nums = [5,5,5,5] 。 第二个查询的总操作次数为 2 + 4 + 1 + 3 = 10 。
示例 2:
输入:nums = [2,9,6,3], queries = [10] 输出:[20] 解释:我们可以将数组中所有元素都增大到 10 ,总操作次数为 8 + 1 + 4 + 7 = 20 。
提示:
n == nums.length
m == queries.length
1 <= n, m <= 105
1 <= nums[i], queries[i] <= 109
思路
首次尝试,暴力超时。
然后,想到直接获取需要增加的次数以及减少的次数,两者相加即可。因此,想到了前缀和,得到小于该元素的所有元素和大于该元素的所有元素即可。但是我们还是得要去找到和queries最相近的数的位置,从而区分左右两边,所以我们需要用到二分查找
代码实现
class Solution {public int binarySearch(int[] nums, int des){//定义初始最小、最大索引int low = 0;int high = nums.length - 1;//确保不会出现重复查找,越界while (low <= high) {//计算出中间索引值int middle = (high + low) >>> 1;//防止溢出if (des == nums[middle]) {return middle;//判断下限} else if (des < nums[middle]) {high = middle - 1;//判断上限} else {low = middle + 1;}}return -1;}public List<Long> minOperations(int[] nums, int[] queries) {List<Long> list = new ArrayList<>();Arrays.sort(nums);int[] a = new int[nums.length];for (int i = 0; i < nums.length; i++) { // 前缀和if (i == 0) {a[i] = nums[i];} else {a[i] = nums[i] + a[i - 1];}}for (int i = 0; i < queries.length; i++) {long sum = 0L;if (nums[nums.length - 1] <= queries[i]) {sum = nums.length * queries[i] - a[nums.length - 1];} else if (nums[0] >= queries[i]) {sum = a[nums.length - 1] - nums.length * queries[i];} else {// 定义初始最小、最大索引int low = 0;int high = nums.length - 1;int index = 0;// 确保不会出现重复查找,越界while (low <= high) {// 计算出中间索引值int middle = (high + low) >> 1;// 防止溢出if (queries[i] >= nums[middle]) {index = middle;low = middle + 1;// 判断下限} else if (queries[i] < nums[middle]) {high = middle - 1;// 判断上限}}sum = queries[i] * (index + 1) - a[index] + a[nums.length - 1] - a[index] - queries[i] * (nums.length - index - 1);}list.add(sum);}return list;}
}6356. 收集树中金币 - 力扣(Leetcode)
给你一个 n 个节点的无向无根树,节点编号从 0 到 n - 1 。给你整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间有一条边。再给你一个长度为 n 的数组 coins ,其中 coins[i] 可能为 0 也可能为 1 ,1 表示节点 i 处有一个金币。
一开始,你需要选择树中任意一个节点出发。你可以执行下述操作任意次:
收集距离当前节点距离为 2 以内的所有金币,或者
移动到树中一个相邻节点。
你需要收集树中所有的金币,并且回到出发节点,请你返回最少经过的边数。
如果你多次经过一条边,每一次经过都会给答案加一。
示例 1:
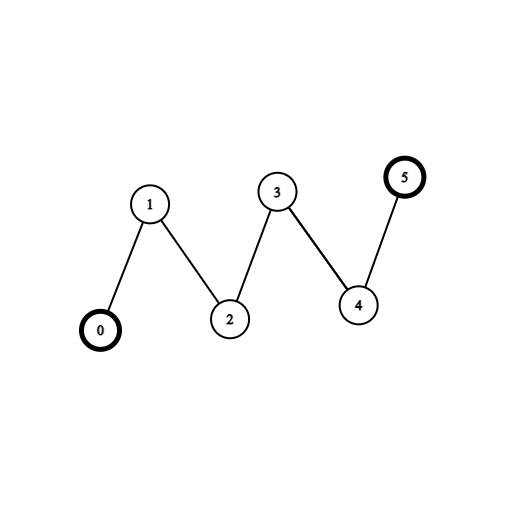
输入:coins = [1,0,0,0,0,1], edges = [[0,1],[1,2],[2,3],[3,4],[4,5]] 输出:2 解释:从节点 2 出发,收集节点 0 处的金币,移动到节点 3 ,收集节点 5 处的金币,然后移动回节点 2 。
示例 2:
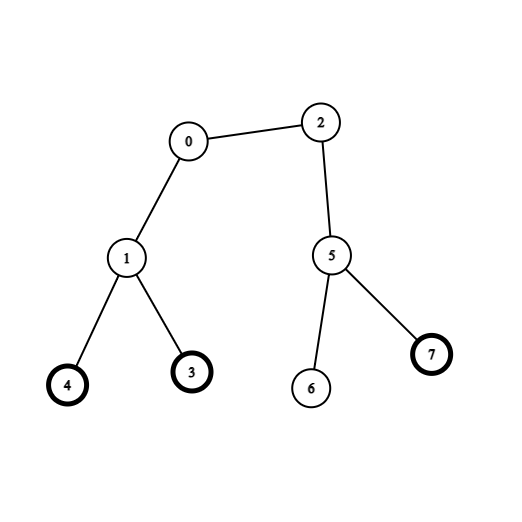
输入:coins = [0,0,0,1,1,0,0,1], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[5,6],[5,7]] 输出:2 解释:从节点 0 出发,收集节点 4 和 3 处的金币,移动到节点 2 处,收集节点 7 处的金币,移动回节点 0 。
提示:
n == coins.length
1 <= n <= 3 * 104
0 <= coins[i] <= 1
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
edges 表示一棵合法的树。
思路
代码实现
相关文章:

【力扣周赛 338】
6354. K 件物品的最大和 - 力扣(Leetcode)袋子中装有一些物品,每个物品上都标记着数字 1、0或 -1。给你四个非负整数 numOnes、numZeros、numNegOnes和 k。袋子最初包含:numOnes 件标记为 1 的物品。numZeroes 件标记为 0 的物品。…...

大数据Flink进阶(八):Apache Flink架构介绍
Apache Flink架构介绍 一、Flink组件栈 在Flink的整个软件架构体系中,同样遵循这分层的架构设计理念,在降低系统耦合度的同时,也为上层用户构建Flink应用提供了丰富且友好的接口。...
Mars3d项目启动上的一些坑
前言 最近新入职了一家公司,公司新开了有个未来城市的项目,需要用到3D城市建模,公司老总选了Mars3d作为前端框架,项目分给我了,又是一个全新的领域,开搞吧! 下面是自己遇到的几个小问题&#x…...

通俗易懂【Springboot】 单文件下载和批量下载(多个文件合成一个压缩包下载)
文章目录一.单文件下载1.简单理解文件下载2.单文件下载的具体代码实现3.测试4.单文件下载整体代码二.多文件批量下载(多个文件合成一个压缩包下载)1.多文件下载的实现方式,这里使用了ZipOutputStream2.具体代码实现3.测试4.文件批量下载&…...

CnOpenData中国行政区划shp数据
一、数据简介 中国行政区划数据是重要的基础地理信息数据,目前不同来源的全国行政区划数据非常多,但能够开放获取的高质量行政区域数据少之又少。基于此,锐多宝的地理空间制作一套2013-2023年可开放获取的高质量行政区划数据。该套数据以2022…...

GPT-4零失误通关大厂模拟面试,offer拿到手软?与AGI首次接触
来源: FoxyearMeta “GPT-4可被视作AGI (通用人工智能)的早期版本。” 如若从他人口中说出,或许是无稽之谈—— 但是由微软雷蒙德研究院机器学习理论组负责人万引大神Sbastien Bubeck与2023新视野数学奖得主Ronen Eldan、2023新晋斯隆研究奖得…...

Hardhat 环境搭建及教程示例
一.安装node.js curl -o- https://raw.githubusercontent.com/nvm-sh/nvm/v0.39.1/install.sh | bash nvm install 18 nvm use 18 nvm alias default 18 npm install npm --global # Upgrade npm to the latest version 二. 安装hardhat 2.1 创建hardhat安装目录 mkdir hard…...

复杂链表的复制-剑指Offer35-java
一、题目描述 请实现 copyRandomList 函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个 next 指针指向下一个节点,还有一个 random 指针指向链表中的任意节点或者 null。 示例 1: 输入:head [[7,null],[13,…...
【Linux】进程理解与学习Ⅰ-进程概念
环境:centos7.6,腾讯云服务器Linux文章都放在了专栏:【Linux】欢迎支持订阅🌹相关文章推荐:【Linux】冯.诺依曼体系结构与操作系统进程概念什么是进程?进程是什么?我们打开任务管理器可以看到有…...

WebKitX ActiveX 6.0 X86 Crack
WebKitX ActiveX将 Chromium Embedded Framework (CEF3) 包装到一个进程外的 ActiveX 组件中,以便与 OLE/COM 语言一起使用。Chromium Embedded Framework 封装了 WebKit Blink HTML5 Renderer 和 Google V8 JavaScript Engine。这是一个用于商业用途的生产级稳定组…...
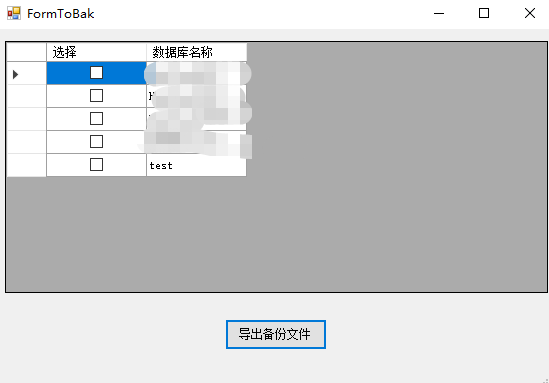
开源项目:数据库表结构生成文档工具
目录 一、软件介绍 二、技术框架 三、功能介绍 四、代码展示 1、获取数据库信息部分代码 2、导出Html文档代码 五、运行效果 六、项目开源地址 一、软件介绍 今天给大家分享我自己编写的数据库表结构文档生成工具,方便大家在实际开发当中,可以很方便导出…...
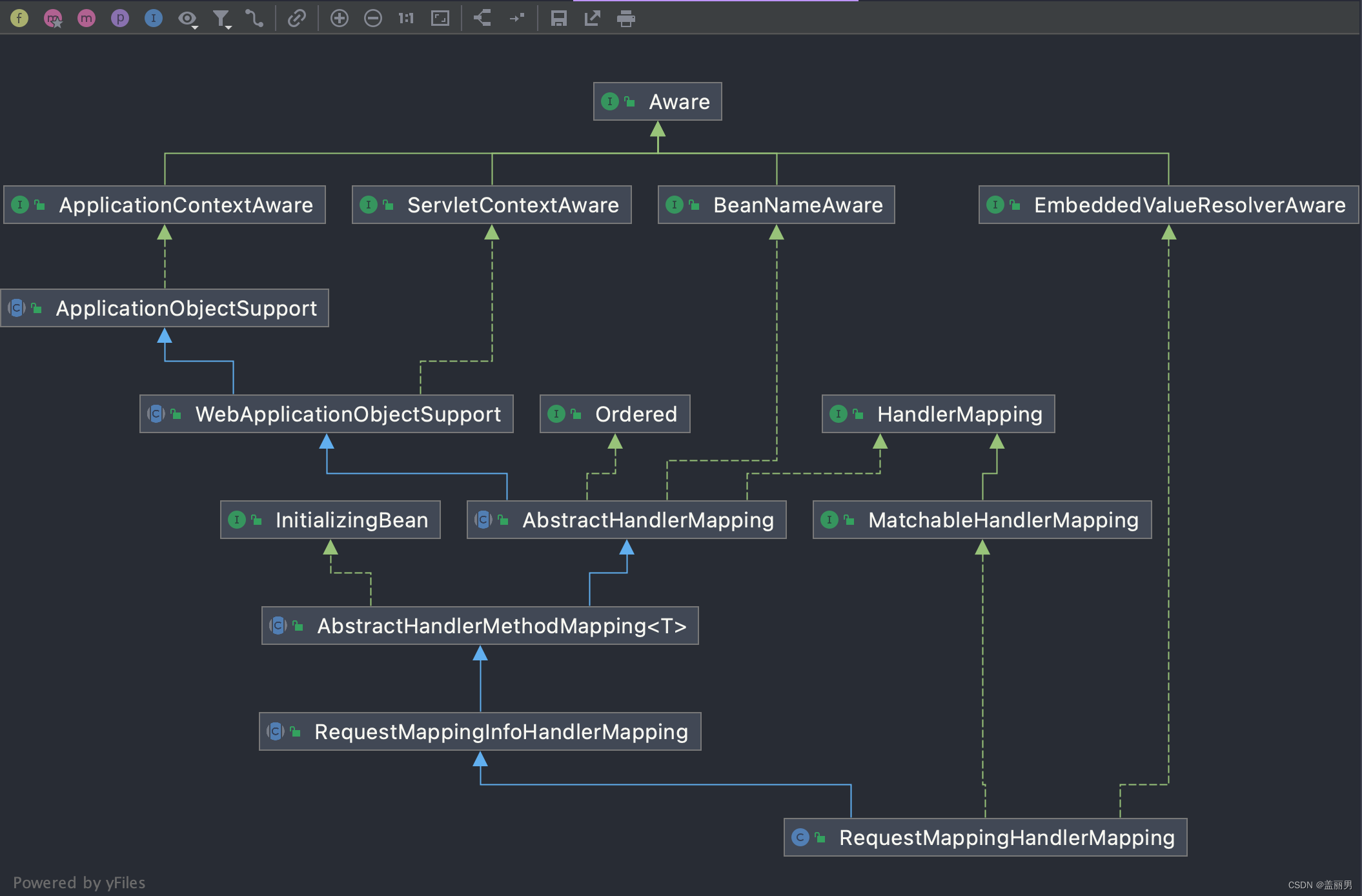
spring的两种拦截器HandlerIntercepter和MethodIntercepter
介绍 Spring有两种拦截器提供给我们使用,一种是HandlerIntercepter,另一种是MethodIntercepter。这两种的来源不同,实现方式也不同,具体的下面来看一下。 HandlerIntercepter 来源 来源于spring-webmvc包 HandlerIntercepter拦…...

初级算法-字符串
主要记录算法和数据结构学习笔记,新的一年更上一层楼! 初级算法-字符串一、反转字符串二、反转字符串(二)三、替换空格四、翻转字符串里的单词五、左旋转字符串六、实现 strStr()七、重复的子字符串字符串中元素只能是字符String…...
| 机考必刷)
华为OD机试题 - 寻找目标字符串(JavaScript)| 机考必刷
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为…...

删除Terminating状态的namespace:cattle-system
这里以cattle-system为例!执行删除命令后namespace(也是用其他k8s object)仍然存在,首先执行 kubectl edit namespace cattle-system 查看是否存在spec.finalizers: kubernetes,如: spec: finalizers:…...
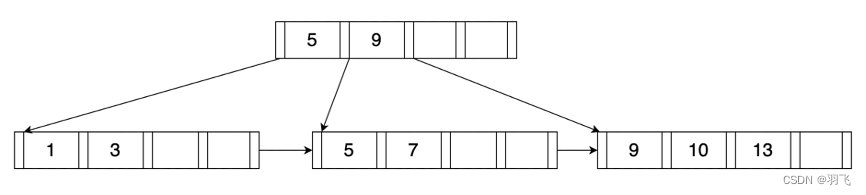
MiniOB 并发B+树实现解析
MiniOB 是 OceanBase 联合华中科技大学推出的一款用于教学的小型数据库系统,希望能够帮助数据库爱好者系统性的学习数据库原理与实战。 B 树介绍 B 树是传统数据库中常见的索引数据结构,比如MySQL、PostgreSQL都实现了B树索引。B 树是一个平衡多叉树&am…...
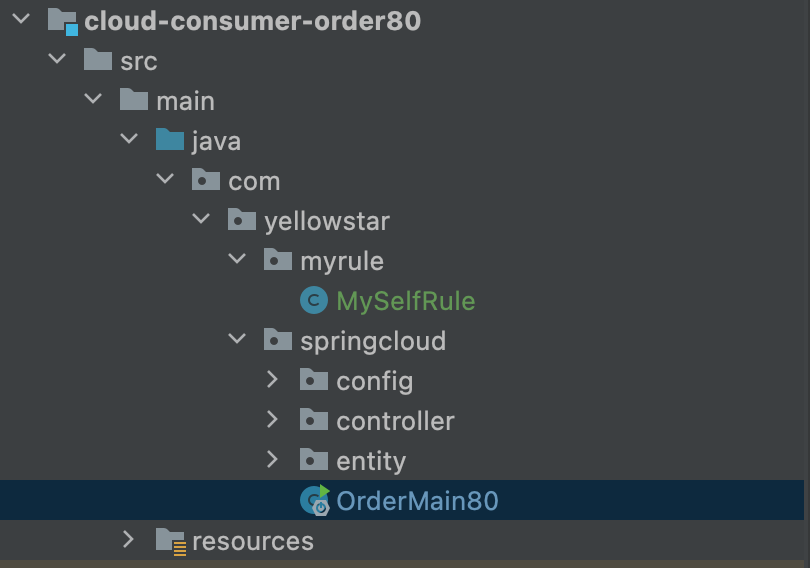
SpringCloud负载均衡服务调用——Ribbon
Ribbon 本专栏学习内容来自尚硅谷周阳老师的视频 有兴趣的小伙伴可以点击视频地址观看 简介 Spring Cloud Ribbon是基于Netflix Ribbon实现的一套客户端负载均衡的工具。 简单的说,Ribbon是Netflix发布的开源项目,主要功能是提供客户端的软件负载均衡算…...

各种邮箱服务软件对比
1.宝塔邮局管理器 特点:简单易用,可视化操作,小白也能搞,还有备份功能,一般足够用了 缺点:稳定性真是差,隔三差五的不能收发.没有接口,不能任意修改邮箱密码,只能管理员修改 注意要点:一定要开启ssl,否则有些邮箱给你发邮件你收不到 建议:不要入坑.坏了之后没法修复,哭都没地方…...

相机单独标定的实现过程[autoware标定]、tmp文件的查看方式
安装了autoware1.13和calibration标定包,发现实现相机单独标定的过程较为坎坷,参考了一些博主的方法,发现下面的过程更加适合自己,做个笔记。 1安装标定箱(与calibration标定包的安装并不冲突) 标定工具箱…...

4.10.1、IP 多播技术的相关基本概念
多播(Multicast,也称为组播)是一种实现 “一对多” 通信的技术,与传统单播“一对一”通信相比,多播可以极大地节省网络资源。 在因特网上进行的多播,称为 IP 多播。 1、单播 & 多播 如下所示…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
