线性判别分析(LDA)中求协方差矩阵示例
让我们通过一个简单的例子计算协方差矩阵。假设我们有两类数据集 X 0 X_0 X0 和 X 1 X_1 X1,每类有两个样本,每个样本有两个特征。
数据集:
类 0 的样本:
X 0 = [ 1 2 2 3 ] X_0 = \begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix} X0=[1223]
类 1 的样本:
X 1 = [ 4 5 5 6 ] X_1 = \begin{bmatrix} 4 & 5 \\ 5 & 6 \end{bmatrix} X1=[4556]
1. 计算每类的均值向量:
首先,我们需要计算每类数据的均值向量。
对于类 0,均值向量 μ 0 \mu_0 μ0:
μ 0 = 1 2 [ 1 + 2 2 + 3 ] = [ 1.5 2.5 ] \mu_0 = \frac{1}{2} \begin{bmatrix} 1+2 \\ 2+3 \end{bmatrix} = \begin{bmatrix} 1.5 \\ 2.5 \end{bmatrix} μ0=21[1+22+3]=[1.52.5]
对于类 1,均值向量 μ 1 \mu_1 μ1:
μ 1 = 1 2 [ 4 + 5 5 + 6 ] = [ 4.5 5.5 ] \mu_1 = \frac{1}{2} \begin{bmatrix} 4+5 \\ 5+6 \end{bmatrix} = \begin{bmatrix} 4.5 \\ 5.5 \end{bmatrix} μ1=21[4+55+6]=[4.55.5]
2. 计算协方差矩阵:
协方差矩阵的公式为:
Σ = 1 n − 1 ∑ i = 1 n ( x i − μ ) ( x i − μ ) T \Sigma = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \mu)(x_i - \mu)^T Σ=n−11i=1∑n(xi−μ)(xi−μ)T
对类 0 计算协方差矩阵 Σ 0 \Sigma_0 Σ0:
我们对每个样本减去均值向量 μ 0 \mu_0 μ0,并计算它们的外积。
对于第一个样本 x 1 = [ 1 , 2 ] x_1 = [1, 2] x1=[1,2],
x 1 − μ 0 = [ 1 2 ] − [ 1.5 2.5 ] = [ − 0.5 − 0.5 ] x_1 - \mu_0 = \begin{bmatrix} 1 \\ 2 \end{bmatrix} - \begin{bmatrix} 1.5 \\ 2.5 \end{bmatrix} = \begin{bmatrix} -0.5 \\ -0.5 \end{bmatrix} x1−μ0=[12]−[1.52.5]=[−0.5−0.5]
对于第二个样本 x 2 = [ 2 , 3 ] x_2 = [2, 3] x2=[2,3],
x 2 − μ 0 = [ 2 3 ] − [ 1.5 2.5 ] = [ 0.5 0.5 ] x_2 - \mu_0 = \begin{bmatrix} 2 \\ 3 \end{bmatrix} - \begin{bmatrix} 1.5 \\ 2.5 \end{bmatrix} = \begin{bmatrix} 0.5 \\ 0.5 \end{bmatrix} x2−μ0=[23]−[1.52.5]=[0.50.5]
接下来,我们计算外积:
( x 1 − μ 0 ) ( x 1 − μ 0 ) T = [ − 0.5 − 0.5 ] [ − 0.5 − 0.5 ] = [ 0.25 0.25 0.25 0.25 ] (x_1 - \mu_0)(x_1 - \mu_0)^T = \begin{bmatrix} -0.5 \\ -0.5 \end{bmatrix} \begin{bmatrix} -0.5 & -0.5 \end{bmatrix} = \begin{bmatrix} 0.25 & 0.25 \\ 0.25 & 0.25 \end{bmatrix} (x1−μ0)(x1−μ0)T=[−0.5−0.5][−0.5−0.5]=[0.250.250.250.25]
( x 2 − μ 0 ) ( x 2 − μ 0 ) T = [ 0.5 0.5 ] [ 0.5 0.5 ] = [ 0.25 0.25 0.25 0.25 ] (x_2 - \mu_0)(x_2 - \mu_0)^T = \begin{bmatrix} 0.5 \\ 0.5 \end{bmatrix} \begin{bmatrix} 0.5 & 0.5 \end{bmatrix} = \begin{bmatrix} 0.25 & 0.25 \\ 0.25 & 0.25 \end{bmatrix} (x2−μ0)(x2−μ0)T=[0.50.5][0.50.5]=[0.250.250.250.25]
协方差矩阵为这两个外积的平均:
Σ 0 = 1 2 − 1 ( [ 0.25 0.25 0.25 0.25 ] + [ 0.25 0.25 0.25 0.25 ] ) = [ 0.5 0.5 0.5 0.5 ] \Sigma_0 = \frac{1}{2-1} \left( \begin{bmatrix} 0.25 & 0.25 \\ 0.25 & 0.25 \end{bmatrix} + \begin{bmatrix} 0.25 & 0.25 \\ 0.25 & 0.25 \end{bmatrix} \right) = \begin{bmatrix} 0.5 & 0.5 \\ 0.5 & 0.5 \end{bmatrix} Σ0=2−11([0.250.250.250.25]+[0.250.250.250.25])=[0.50.50.50.5]
对类 1 计算协方差矩阵 Σ 1 \Sigma_1 Σ1:
同样地,对类 1 的样本进行相同的步骤。
对于第一个样本 x 1 = [ 4 , 5 ] x_1 = [4, 5] x1=[4,5],
x 1 − μ 1 = [ 4 5 ] − [ 4.5 5.5 ] = [ − 0.5 − 0.5 ] x_1 - \mu_1 = \begin{bmatrix} 4 \\ 5 \end{bmatrix} - \begin{bmatrix} 4.5 \\ 5.5 \end{bmatrix} = \begin{bmatrix} -0.5 \\ -0.5 \end{bmatrix} x1−μ1=[45]−[4.55.5]=[−0.5−0.5]
对于第二个样本 x 2 = [ 5 , 6 ] x_2 = [5, 6] x2=[5,6],
x 2 − μ 1 = [ 5 6 ] − [ 4.5 5.5 ] = [ 0.5 0.5 ] x_2 - \mu_1 = \begin{bmatrix} 5 \\ 6 \end{bmatrix} - \begin{bmatrix} 4.5 \\ 5.5 \end{bmatrix} = \begin{bmatrix} 0.5 \\ 0.5 \end{bmatrix} x2−μ1=[56]−[4.55.5]=[0.50.5]
外积分别为:
( x 1 − μ 1 ) ( x 1 − μ 1 ) T = [ 0.25 0.25 0.25 0.25 ] (x_1 - \mu_1)(x_1 - \mu_1)^T = \begin{bmatrix} 0.25 & 0.25 \\ 0.25 & 0.25 \end{bmatrix} (x1−μ1)(x1−μ1)T=[0.250.250.250.25]
( x 2 − μ 1 ) ( x 2 − μ 1 ) T = [ 0.25 0.25 0.25 0.25 ] (x_2 - \mu_1)(x_2 - \mu_1)^T = \begin{bmatrix} 0.25 & 0.25 \\ 0.25 & 0.25 \end{bmatrix} (x2−μ1)(x2−μ1)T=[0.250.250.250.25]
协方差矩阵为:
Σ 1 = 1 2 − 1 ( [ 0.25 0.25 0.25 0.25 ] + [ 0.25 0.25 0.25 0.25 ] ) = [ 0.5 0.5 0.5 0.5 ] \Sigma_1 = \frac{1}{2-1} \left( \begin{bmatrix} 0.25 & 0.25 \\ 0.25 & 0.25 \end{bmatrix} + \begin{bmatrix} 0.25 & 0.25 \\ 0.25 & 0.25 \end{bmatrix} \right) = \begin{bmatrix} 0.5 & 0.5 \\ 0.5 & 0.5 \end{bmatrix} Σ1=2−11([0.250.250.250.25]+[0.250.250.250.25])=[0.50.50.50.5]
结果:
对于类 0 和类 1,它们的协方差矩阵分别为:
Σ 0 = [ 0.5 0.5 0.5 0.5 ] \Sigma_0 = \begin{bmatrix} 0.5 & 0.5 \\ 0.5 & 0.5 \end{bmatrix} Σ0=[0.50.50.50.5]
Σ 1 = [ 0.5 0.5 0.5 0.5 ] \Sigma_1 = \begin{bmatrix} 0.5 & 0.5 \\ 0.5 & 0.5 \end{bmatrix} Σ1=[0.50.50.50.5]
这是一个简单的二维数据集协方差矩阵的计算例子。
相关文章:
中求协方差矩阵示例)
线性判别分析(LDA)中求协方差矩阵示例
让我们通过一个简单的例子计算协方差矩阵。假设我们有两类数据集 X 0 X_0 X0 和 X 1 X_1 X1,每类有两个样本,每个样本有两个特征。 数据集: 类 0 的样本: X 0 [ 1 2 2 3 ] X_0 \begin{bmatrix} 1 & 2 \\ 2 & 3…...
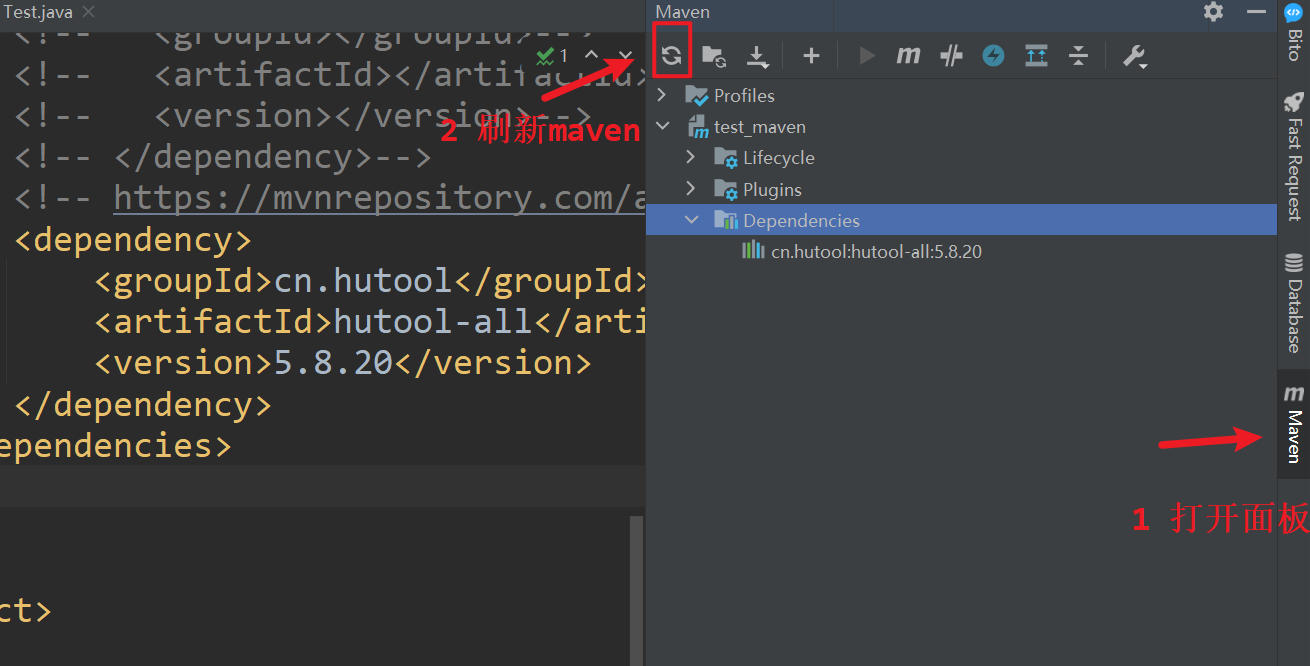
Maven的详细解读和配置
目录 一、Maven 1.1 引言 1.2 介绍 1.3 下载安装 1.3.1 解压 1.3.2 配置环境变量 1.3.3 测试 1.4 仓库[了解] 1.5 Maven配置 1.5.1 修改仓库位置 1.5.2 设置镜像 二、IDEA - MAVEN 2.1 idea关联maven 2.2 为新项目设置 2.2 创建java项目[重点] 2.3 java项目结构…...

在vue2项目中使用dart-sass
问题描述 在vue2项目中使用dart-sass。或者将node-sass换成dart-sass,原因是node-sass安装比较困难,很多时候sass-loader无法安装成功。另外在win和Linux环境下运行行项目需要针对Linux搞一个node-sass的Linux版本。 问题分析 在 Vue 2 项目中使用 da…...

【机器学习】过拟合与欠拟合——如何优化模型性能
【机器学习】过拟合与欠拟合——如何优化模型性能 1. 引言 在机器学习中,模型的表现不仅依赖于算法的选择,还依赖于模型对数据的拟合情况。过拟合(Overfitting)和欠拟合(Underfitting)是模型训练过程中常…...

二进制日志gtid模式
# --skip-gtids,使用mysqlbinlog截取时添加该参数,会执行已经执行的事务 mysqlbinlog --skip-gtids --include-gtidsa56fdfdc-7699-11ef-8f40-000c297f81d5:40 /data/binlog/mysql-bin.000003 > gtid.sql # --skip-gtids,使用mysqlbinlog截…...

华硕主板开启TPM 2.0
安装Windows11系统,需要打开TPM 安装 Windows 11 的方法 电脑健康状况检查应用验证最低系统要求 在电脑上启用 TPM 2.0 查看主板型号 winr msinfo32 查看 tpm 进入Advanced Mode(F7) 选择Security,进入Secure Boot,我…...

Linux 一键部署Mysql 8.0.37
mysql 前言 MySQL 是一个基于 SQL(Structured Query Language)的数据库系统,SQL 是一种用于访问和管理数据库的标准语言。MySQL 以其高性能、稳定性和易用性而闻名,它被广泛应用于各种场景,包括: Web 应用程序:许多动态网站和内容管理系统(如 WordPress)使用 MySQL 存…...

Elasticsearch可视化工具ElasticHD
目录 介绍 ElasticHD应用程序页面 安装 基本用法 独立可执行文件 ES版本支持 SQL特性支持: 超越SQL功能支持: SQL的用法 Docker快速入门: 下载地址 介绍 ElasticHD是ElasticSearch可视化管理工具。它不需要任何软件。它在您的Web浏览器中工作,允许您随时随地管理…...

Chrome截取网页全屏
1.使用Chrome开发者工具 Chrome自带的开发者工具,可以进行网页整页截图, 首先打开你想截图的网页, 然后按下 F12,调出开发者工具, 接着按Ctrl Shift P。 紧接着输入指令 capture, 它会提示有三个选项,如…...

Why Is Prompt Tuning for Vision-Language Models Robust to Noisy Labels?
文章汇总 本文的作者针对了提示学习的结构设计进行了分析,发现了一些规律: 1)固定的类名令牌为模型的优化提供了强正则化,减少了由噪声样本引起的梯度。 2)从多样化和通用的web数据中学习到的强大的预训练图像文本嵌入为图像分类提供了强大…...

C++ 折叠表达式
C 折叠表达式(Fold Expression)是在 C17 引入的一种语法,用于简化与可变参数模板的操作。折叠表达式的作用是对参数包(parameter pack)进行递归处理。 折叠表达式有四种类型: 一元左折叠 (Unary Left Fol…...
双控开关接入NVBoard
导入NVBoard git仓库:https://github.com/NJU-ProjectN/nvboard 按照ysyx手册的要求,初始化NVBoard项目。 由于GitHub在国外,可能会超时无响应: 解决方案是修改代理。 当前的运行环境是VM VirtualBox虚拟机,网卡是…...

聊一聊软件系统性能测试的重要性
目录 性能测试的分类 为什么要进行性能测试呢? 性能测试曲线对比参数 虚拟用户数 vs 时间: 响应时间 vs 虚拟用户数: 吞吐量 vs 虚拟用户数: 错误率 vs 虚拟用户数: 资源使用情况 vs 时间: 组合视图 上图曲线图关键点介绍 性能测试的重要性主要体现在以下…...

双十一有哪些好物值得入手?五款超值数码好物分享!
在如今这个科技飞速发展的时代,数码产品已经成为我们生活中不可或缺的一部分。双十一作为一年一度的购物狂欢节,为我们提供了一个绝佳的机会,可以以更优惠的价格入手心仪的数码好物。下面就为大家分享五款超值数码好物,让你的生活…...

uniapp监听滚动实现顶部透明度变化
效果如图: 实现思路: 1、使用onPageScroll监听页面滚动,改变导航条的透明度; 2、关于顶部图片的高度: 如果是小程序:使用getMenuButtonBoundingClientRect获取胶囊顶部距离和胶囊高度; 如果…...

Humanoid 3D Charactor_P08_Federica
3D模型(人形装备)女孩 “P08_联邦” 内容仅为3D人物模型。 图片中的背景和家具不包括在内。 由Blender制作 包括: 1. 人形机器人3D模型和材质。 2. “Unity-chan!”着色器。 性别:女 装备:人形 皮肤网格:4个骨骼权重 多边形: 20000~40000 纹理分辨率:2K纹理 混合形状:…...

TikTok直播推流不精准该怎么办?跟IP有关系吗?
TikTok,这款风靡全球的短视频社交平台,其直播功能已成为众多创作者与品牌宣传的利器。然而,不少用户却遭遇了直播推流不精准的难题,这直接影响到直播的曝光和互动效果。那么,面对这一问题,我们该如何应对&a…...

Docker Registry API best practice 【Docker Registry API 最佳实践】
文章目录 1. 安装 docker2. 配置 docker4. 配置域名解析5. 部署 registry6. Registry API 管理7. 批量清理镜像8. 其他 👋 这篇文章内容:实现shell 脚本批量清理docker registry的镜像。 🔔:你可以在这里阅读:https:/…...

便捷点餐:Spring Boot 点餐系统
第三章 系统分析 3.1 系统设计目标 网上点餐系统主要是为了用户方便对美食信息、美食评价、美食资讯等信息进行查询,也是为了更好的让管理员进行更好存储所有数据信息及快速方便的检索功能,对系统的各个模块是通过许多今天的发达系统做出合理的分析来确定…...

研一上课计划2024/9/23有感
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、学位课1.应用数理统计(学3 开卷考试)2.最优化方法(学3 开卷考试)3.新中特(学2 三千五百字的品读…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

免费批量Markdown转Word工具
免费批量Markdown转Word工具 一款简单易用的批量Markdown文档转换工具,支持将多个Markdown文件一键转换为Word文档。完全免费,无需安装,解压即用! 官方网站 访问官方展示页面了解更多信息:http://mutou888.com/pro…...

记一次spark在docker本地启动报错
1,背景 在docker中部署spark服务和调用spark服务的微服务,微服务之间通过fegin调用 2,问题,docker容器中服务器来后,注册中心都有,调用服务也正常,但是调用spark启动任务后报错,报错…...
