MATLAB系列06:复数数据、字符数据和附加画图类
MATLAB系列06:复数数据、字符数据和附加画图类
- 6. 复数数据、字符数据和附加画图类
- 6.1 复数数据
- 6.1.1 复变量( complex variables)
- 6.1.2 带有关系运算符的复数的应用
- 6.1.3 复函数( complex function)
- 6.1.4 复数数据的作图
- 6.2 字符串函数
- 6.2.1 字符转换函数
- 6.2.2 创建二维字符数组
- 6.2.3 字符串的连接
- 6.2.4 字符串的比较
- 6.2.5 在一个字符串中查找/替换字符
- 6.2.6 大小写转换
- 6.2.7 字符串转为数字
- 6.2.8 数字转为字符串
- 6.2.9 字符串函数总结
- 6.3 多维数组
- 6.4 关于二维作图的补充说明
- 6.4.1 二维作图的附加类型
- 6.4.2 作图函数
- 6.4.3 柱状图
- 6.5 三维作图
- 6.5.1 三维曲线作图
- 6.5.2 三维表面,网格,等高线图象
- 6.6 总结
6. 复数数据、字符数据和附加画图类
6.1 复数数据
复数是指既包含实部又包含虚部的数。复数的一般形式如下:
C = a + b i C=a+bi C=a+bi
MATLAB 用直角坐标表达复数。每一个复数应有一对实数(a, b)组成。第一个数(a)代表复数的实部,第二个数( b)代表复数的虚部。
6.1.1 复变量( complex variables)
MATLAB将自动创建一个复变量。创建复数的最简单方法是用MATLAB本自带的因有变量i或j, 它们都被预定义为 -1 。 示例:
>> c1 = 4 + 3*ic1 =4.0000 + 3.0000i
6.1.2 带有关系运算符的复数的应用
用关系运算符 = = == ==来判断两复数是否相等,或用关系运算符~=判断两复数是否不相等,这种情况是可能的。这些运算都会产生出我们所期望的结果。例如,如果 c1=4+3i 和 c2=4-3i,那么关系运算 c1==c2 将会产生 0,关系运算 c1~=c2 将会产生 1。
但是,比较运算符>, <, <=或>=将不会产生我们所期望的结果。当复数进行此类关系运算时,只对复数的实部进行比较。例如,如果 c1=4+i3 和 c2=4+i8,那么比较运算 c1>c2将会产生 1,尽管 c1 的模要比 c2 的模小。如果我们需要用这些运算对两复数进行比较,我们更加关心的是两复数的模,而不只是实部。复数的模可以由 abs 固有函数计算得到。
6.1.3 复函数( complex function)
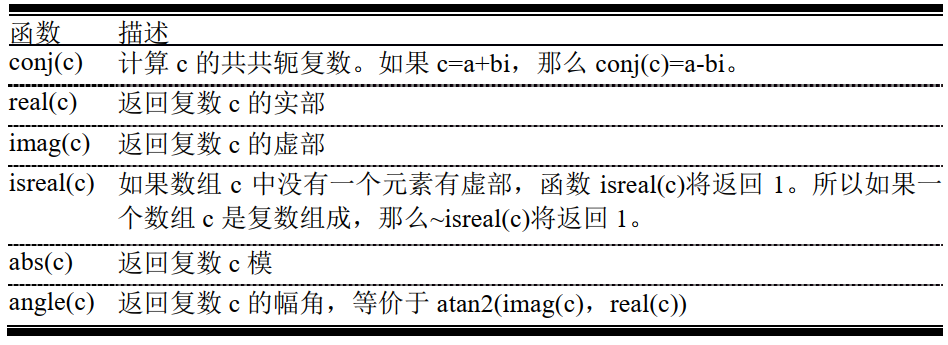
6.1.4 复数数据的作图
因为复数数据既包括实部又包括虚部,所以在 MATLAB 中复数数据的作图与普通实数据的作图有所区别。例如,考虑下面的函数
y ( t ) = e − 0.2 t ( c o s t + i sin t ) y(t)=e^{-0.2t}\left(cost+i\sin t\right) y(t)=e−0.2t(cost+isint)
如果我们用传统的 plot 命令给这个函数作图,只有实数数据被作出来,而虚部将会被忽略。
方式一:在相同的时间轴画出函数的实部和虚部
t = 0:pi/20:4*pi;
y = exp(-0.2*t) .* (cos(t) + i * sin(t));
plot(t, real(y),'b-');
hold on;
plot(t, imag(y),'r--');
title('\bfPlot of Complex Function vs Time');
xlabel('\bf\itt');
ylabel('\bf\ity(t)');
legend('real','imaginary');
hold off;
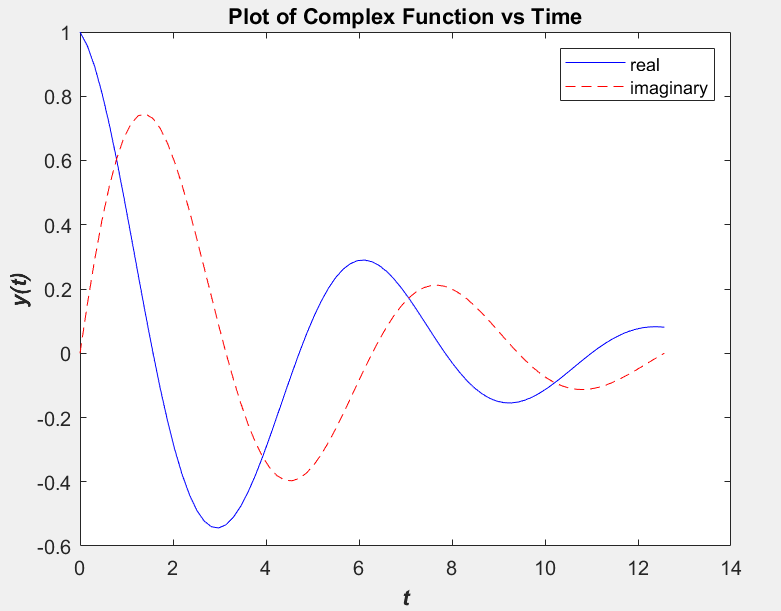
方式二:如果有一个复参数提供给plot函数它会自动产生一个函数的实部-虚部
t = 0:pi/20:4*pi;
y = exp(-0.2*t) .* (cos(t) + i * sin(t));
plot(y,'b-');
title('\bfPlot of Complex Function');
xlabel('\bfReal Part');
ylabel('\bfImaginary Part');
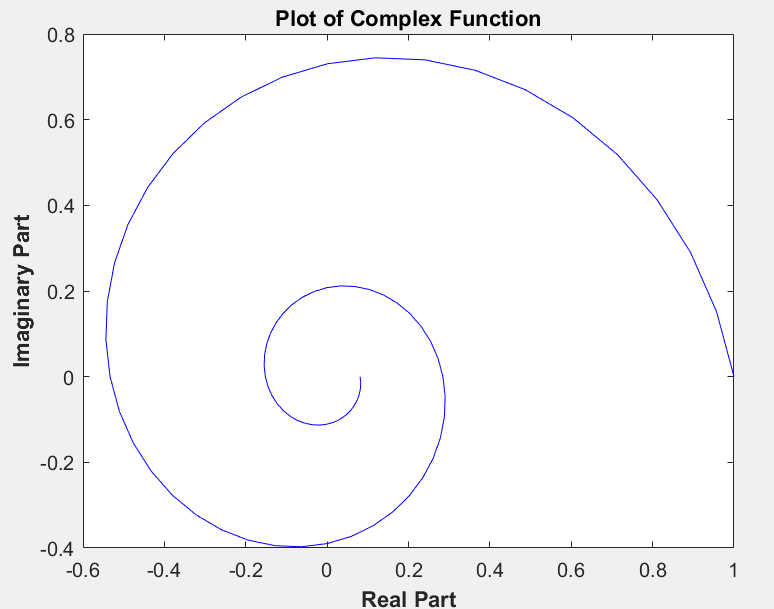
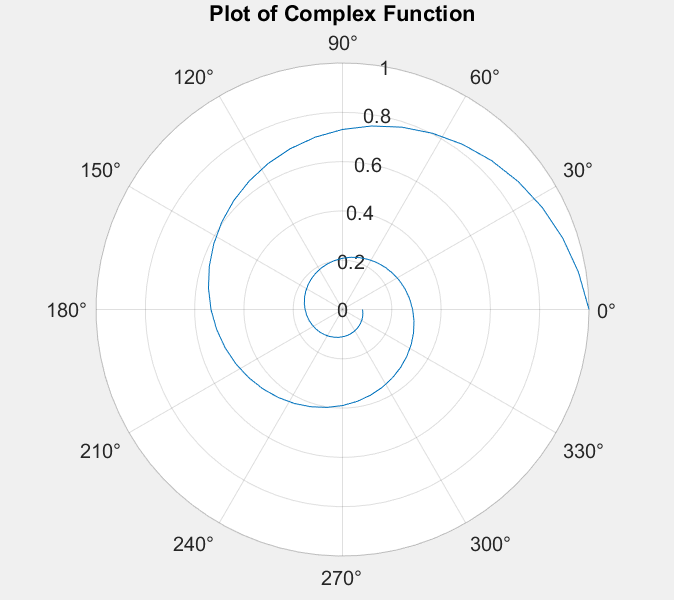
方式三:画出极坐标图
t = 0:pi/20:4*pi;
y = exp(-0.2*t) .* (cos(t) + i * sin(t));
polarplot(angle(y),abs(y));
title('\bfPlot of Complex Function');
6.2 字符串函数
一个 MATLAB 字符串是一个 char 型数组。每一个字型占两个字节。当字符串被赋值于一个变量时,这个变量将被自动创建为字符变量。 示例:
>> str='hello world!';
>> whos strName Size Bytes Class Attributesstr 1x12 24 char
6.2.1 字符转换函数
我们可以利用 double 函数把变量从字型转化为 double 型。
>> x=double(str)x =104 101 108 108 111 32 119 111 114 108 100 33
我们可以利用 char 函数把 double 型数据转化为字符型数据。所以函数 char(x)产生的结果
>> x=char(x)x ='hello world!'
6.2.2 创建二维字符数组
我们可以创建二维字符数组,但一个数组中每一行的长度都必须相等。如果其中的一行比其他行短,那么这个字符数据将会无效,并产生一个错误。例如,下面的语句是非法的,因为他两行的长度不同。
name = ['Stephen J. Chapman'; 'Senior Engineer'];
创建二维字符数组的最简单的方法是用 char 函数。函数将会自动地寻找所有字符串中最长的那一个。其他用空格补全
>> name = char('Stephen J. Chapman','Senior Engineer')name =2×18 char 数组'Stephen J. Chapman''Senior Engineer '
我们可以应用 deblank 函数去除多余空格。例如,下面的语句去除 name 数组中第二行的多余空格,产生的结果与原来的进行比较。
>> line2 = name(2,:)line2 ='Senior Engineer '>> line2_trim = deblank(name(2,:))line2_trim ='Senior Engineer'>> size(line2)ans =1 18>> size(line2_trim)ans =1 15
6.2.3 字符串的连接
函数 strcat 水平连接两字符串,忽略所有字符串末端的空格,而字符串的空格保留。示例:
>> result = strcat('string 1 ','String 2')result ='string 1String 2'
函数 strvcat 用于竖直地连接两字符串,自动地把它转化为二维数组。示例:
>> result = strvcat('Long String 1 ','String 2')result =2×14 char 数组'Long String 1 ''String 2 '
6.2.4 字符串的比较
-
比较两字符串,看是否相同
-
strcmp判断两字符串是否等价 -
strcmpi忽略大小写判断两字符串是否等价 -
strncmp判断两字符串前 n 个字符是否等价 -
strncmpi忽略大小写判断两字符串前 n 个字符是否等价
-
-
判断单个字符是否相等
我们可以利用 MATLAB 关系运算符对字符数组中的每一个元素进行检测,看是否相同,但是我们要保证它们的维数是相同的,或其中一个是标量。例如,你可以用相等运算符( ==)来检测两字符串是否相匹配。
>> a = 'fate'; >> b = 'cake'; >> result = a == bresult =1×4 logical 数组0 1 0 1所有的关系运算符( >, >=, <, <=, ==, ~=)都是对字符所对应的 ASCII 值进行比较。与 C 语言不同, MATLAB 中没有一个内建函数,对两字符串在整体进行“大于”或“小于”的关系运算。
-
在一字符串内对字符进行判断
有两个函数可对一个字符串内的字符逐个进行分类。
isletter用来判断一个字符是否为字母isspace判断一个字符是否为空白字符(空格, tab,换行符)
示例:
>> mystring = 'Room 23a'mystring ='Room 23a'>> a = isletter(mystring)a =1×8 logical 数组1 1 1 1 0 0 0 1
6.2.5 在一个字符串中查找/替换字符
MATLAB 提供了许多的函数,用来对字符串中的字符进行查找或替换。
-
函数
findstr返回短字符串在长字符串中所有的开始位置。示例:>> test = 'This is a test!'; >> position = findstr(test,'is')position =3 6 -
函数
strmatch是另一种匹配函数。它用来查看二维数组行开头的字符,并返回那些以指定的字符序列为开头行号。示例:>> array = strvcat('maxarray','min value','max value')array =3×9 char 数组'maxarray ''min value''max value'>> result = strmatch('max',array)result =13 -
函数
strrep用于进行标准的查找和替换操作。它能找到一个字符串中的所有另一个字符串,并被第三个字符串替换。这个函数形式为result = strrep(str,srch,repl)其中 str 是被检测的字符串, srch 是要查找到的字符串, repl 是用于替代的字符串,示例:
>> test='This is a test!'test ='This is a test!'>> result = strrep(test,'test','pest')result ='This is a pest!' -
函数
strtok返回输入字符串中第一次出现在分隔符前面的所有字符。默认的分隔符为一系列的空白字符。strtok的形式如下[token, remainder] = strtok(string, delim)其中 string 是输入字符串, delim 是可选择的分隔符, token 代表输入字符串中第一次出现在分隔符前面的所有字符, remainder 代表这一行的其余部分。例子:
>> [token, remainder] = strtok('This is a test!')token ='This'remainder =' is a test!'你可以利用函数strtok把一个句子转换为单词。
6.2.6 大小写转换
函数 upper 和 lower 分别把一个字符串中所有转化大定和小写。例如
>> result = upper('This is test 1!')result ='THIS IS TEST 1!'>> result = lower('This is test 2!')result ='this is test 2!'
在大小转换时,数字和符号不受影响。
6.2.7 字符串转为数字
MATLAB 把由数字组成的字符串转化为数字要用到函数 eval。示例:
>> a = '3.141592';
>> b = eval(a)b =3.1416
字符串可以用 sscanf 函数转化为数字。 函数 sscanf 两种最普通的转义序是“%d”,“%g”,它们分别代表输出为整数或浮点数。示例:
>> value1 = sscanf('3.141593','%g')value1 =3.1416>> value2 = sscanf('3.141593','%d')value2 =3
6.2.8 数字转为字符串
MATLAB 中有许多的字符串/数字转换函数把数字转化为相应的字符串。我们在这里只看两个函数 num2str 和 int2str。示例:
>> x=5317;
>> y=int2str(x);
>> whos yName Size Bytes Class Attributesy 1x4 8 char >> whos xName Size Bytes Class Attributesx 1x1 8 double
函数 num2str 为输出字符串的格式提供更多的控制。第二个可选择的参数可以对输出字符串的数字个数进行设置或指定一个实际格式。例如:
>> p=num2str(pi,7)p ='3.141593'>> p=num2str(pi,'%10.5e')p ='3.14159e+00'
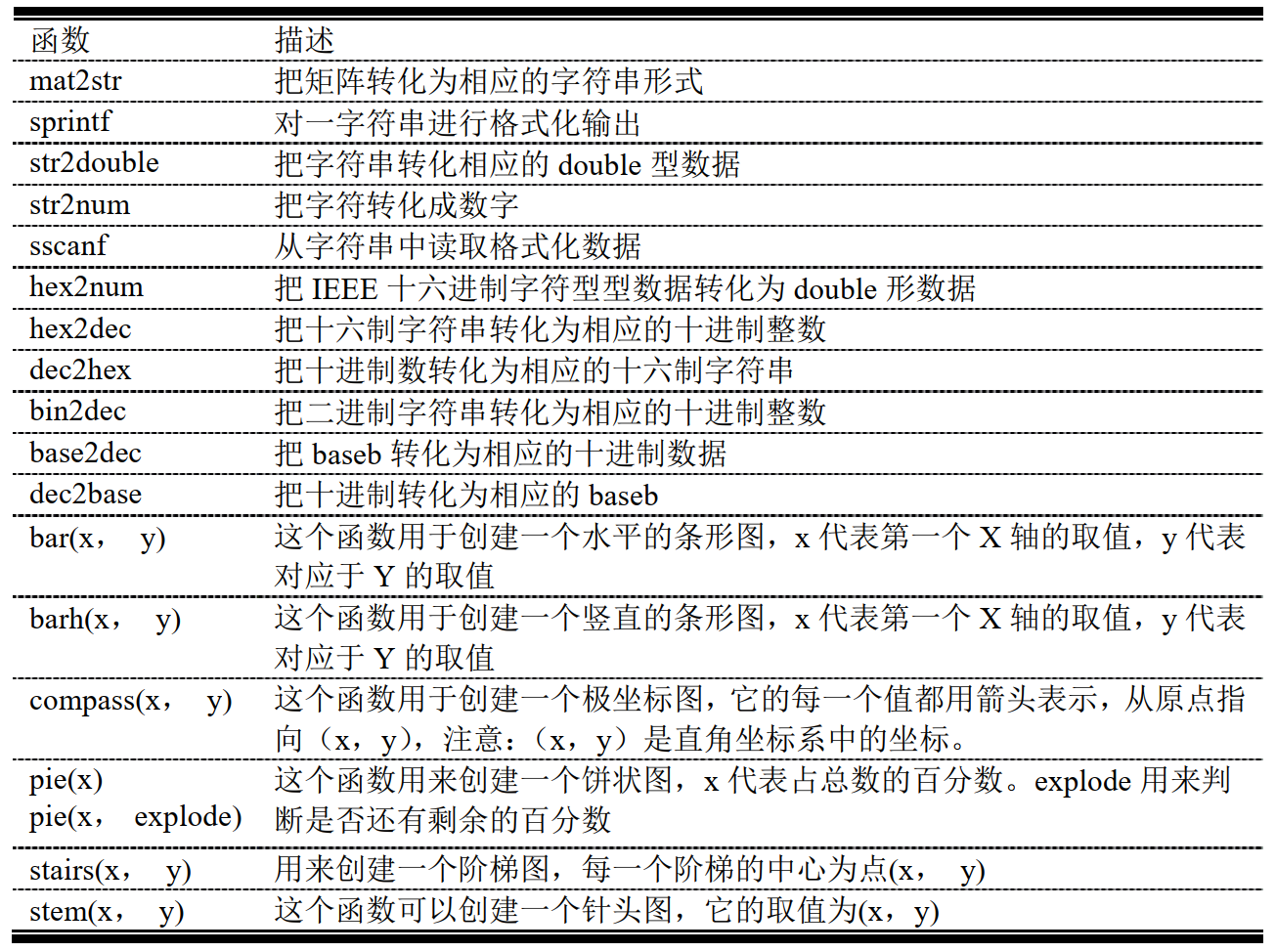
6.2.9 字符串函数总结


6.3 多维数组
多维数组是二维数组的扩展。每增加一维,它们所对应的每个元素就会多一个下角标。示例:
>> a=[1 2 3 4;5 6 7 8]a =1 2 3 45 6 7 8>> a(:,:,2)=[9 10 11 12;13 14 15 16];
>> a(:,:,3)=[17 18 19 20;21 22 23 24]a(:,:,1) =1 2 3 45 6 7 8a(:,:,2) =9 10 11 1213 14 15 16a(:,:,3) =17 18 19 2021 22 23 24>> a(1,1,2)ans =9>> a(1,1,:)ans(:,:,1) =1ans(:,:,2) =9ans(:,:,3) =17
6.4 关于二维作图的补充说明
6.4.1 二维作图的附加类型
在 MATLAB 帮助工作台中列出超过 20 种类型的作图。例如针头图(Stem Plots),阶梯图(stair plots), 条形图,饼图(pie plots),罗盘图(compass plots)。 在针头图中的每一个值都用一个圆圈和垂直于 x轴的直线连接而成。在阶梯图中的每一个值都是用连续的竖直的长条线来表示,形成阶梯状效果。条形图可分成水平条形图和竖直条形图。饼图用不同的扇区代表不同的变量。最后罗盘图是另一种极坐标图它的每一值用箭头来表示。

-
条形图
x = [1 2 3 4 5 6]; y = [2 6 8 7 8 5]; bar(x,y); title('\bfExample of a Bar Plot'); xlabel('\bf\itx'); ylabel('\bf\ity'); axis([0 7 0 10]);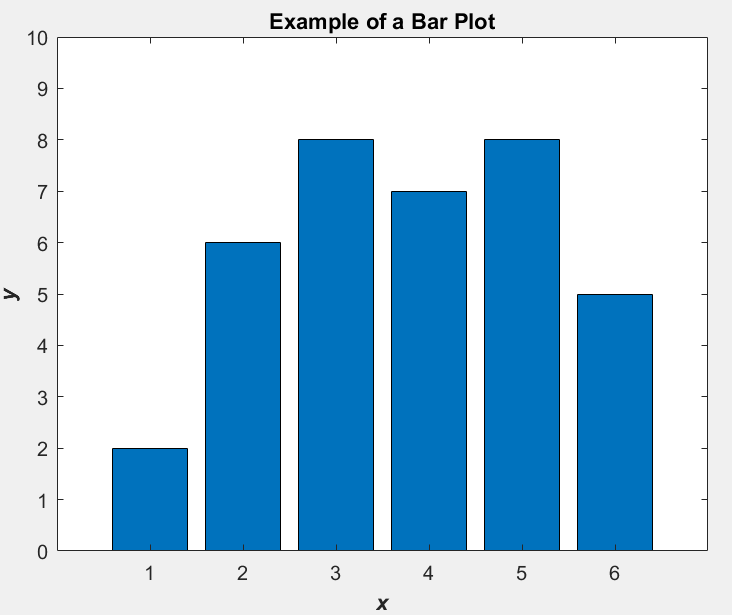
-
阶梯图
x = [1 2 3 4 5 6]; y = [2 6 8 7 8 5]; stairs(x,y); title('\bfExample of a Stairs Plot'); xlabel('\bf\itx'); ylabel('\bf\ity'); axis([0 7 0 10]);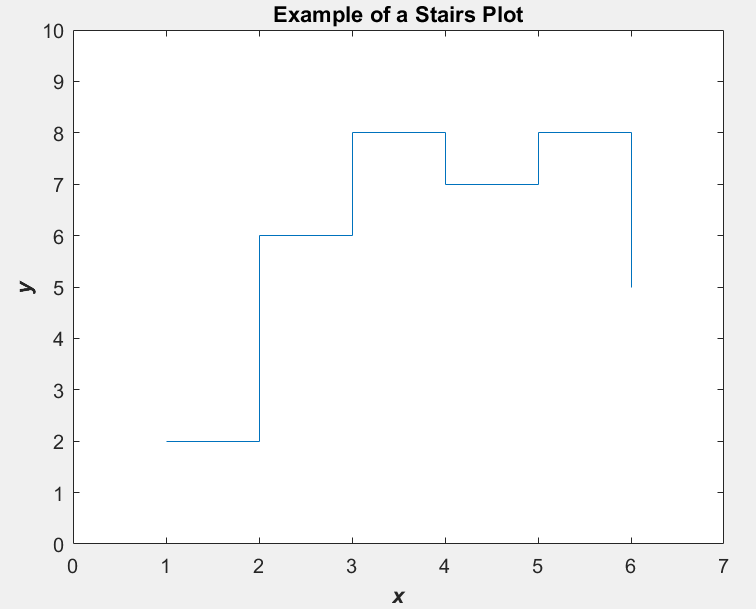
-
极坐标图
x = [1 2 3 4 5 6]; y = [2 6 8 7 8 5]; compass(x,y); title('\bfExample of a Compass Plot'); xlabel('\bf\itx'); ylabel('\bf\ity'); axis([0 7 0 10]);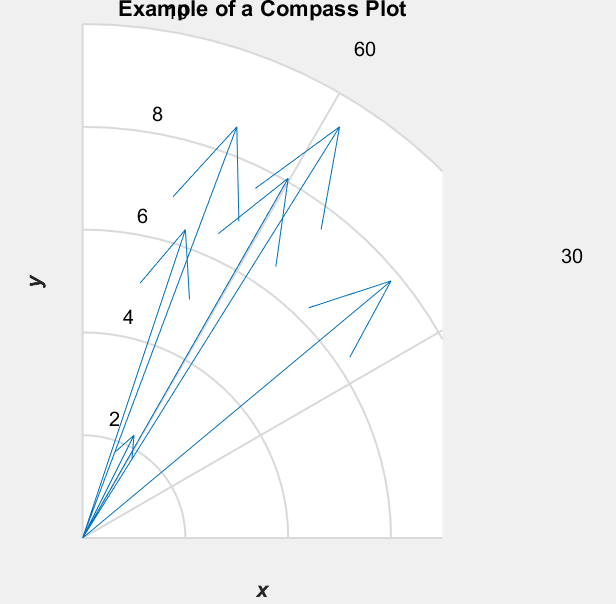
-
饼状图
data = [10 37 5 6 6]; explode = [0 1 0 0 0]; pie(data, explode); title('\bfExample of a Pie Plot'); legend('One','Two','Three','Four','Five');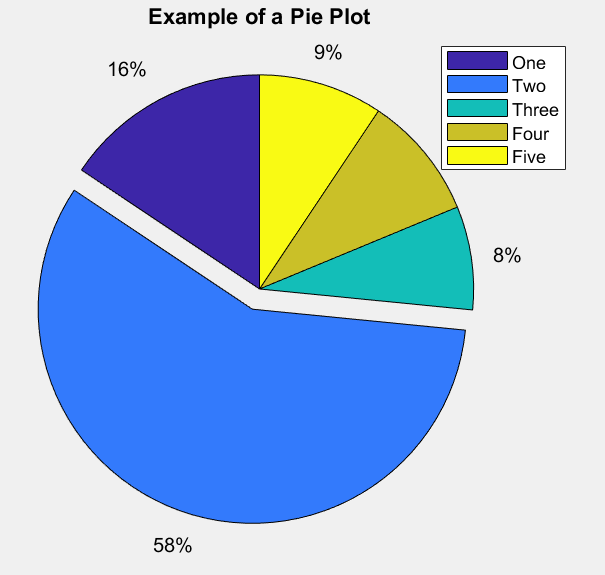
-
针头图
x = [1 2 3 4 5 6]; y = [2 6 8 7 8 5]; stem(x,y); title('\bfExample of a Stem Plot'); xlabel('\bf\itx'); ylabel('\bf\ity'); axis([0 7 0 10]);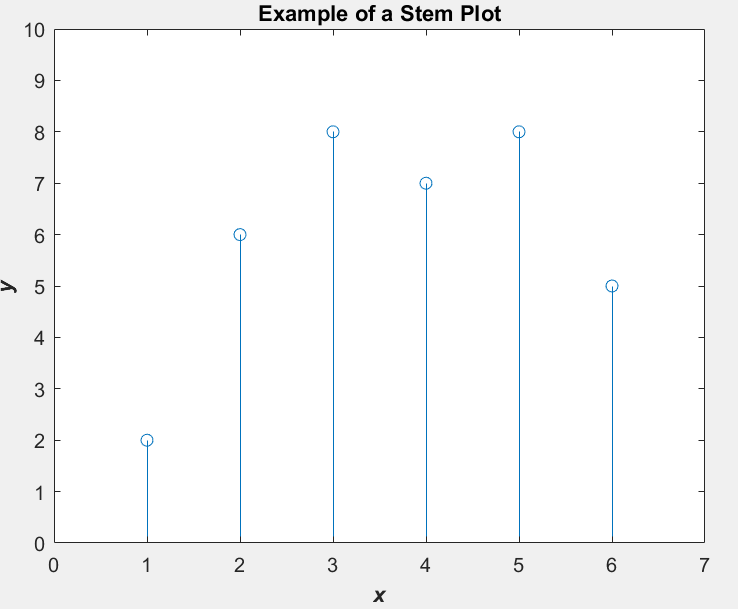
6.4.2 作图函数
在前面的所有作图,我们必须创建数组,并把这些数组传递给作图函数。 MATLAB 提供了两个函数可以直接作出图象,而不需要创建中间数据数组。它们是函数数 ezplot 和 fplot。示例:
ezplot('sin(x)/x',[-4*pi 4*pi]);
title('Plot of sinx/x');
grid on;
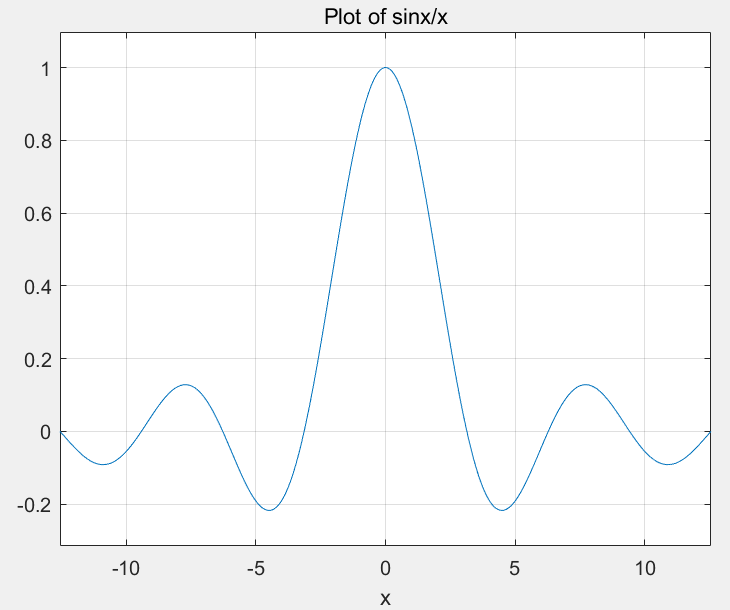
函数 fplot 与 ezplot 相类似,但更加精确。前两个参数与函数 ezplot 中的相同,但是函数 fplot 还有其他优点。
- 函数 fplot 是适应性的,它意味着在自变量范围内函数突然变化显示更多的点。
- 函数 fplot 支持 TEX 命令,用来指定坐标图的标题和坐标轴标签,而函数 ezplot 则不能。
在一般情况下,在画函数图象时,你应当使用函数 fplot。
6.4.3 柱状图
柱状图用来显示一系列数据数值的分布。为了创建一个柱状图,在一系列数值中范围被平均划分,并确定某一个范围中数值的个数。 示例:
y = randn(10000, 1);
hist(y, 15);
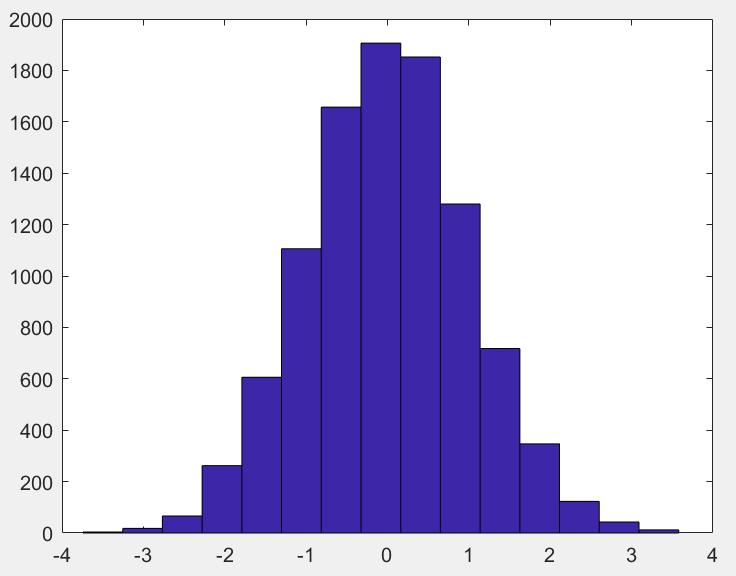
该语句创建一个包含有 1000 个符合正分布的随机数数组并产生了一个取值范围 15 等分的柱状图。
6.5 三维作图
6.5.1 三维曲线作图
t = 0:0.1:10;
x = exp(-0.2*t) .* cos(2*t);
y = exp(-0.2*t) .* sin(2*t);
plot3(x,y,t);
title('\bfThree-Dimensional Line Plot');
xlabel('\bfx');
ylabel('\bfy');
zlabel('\bfTime');
axis square;
grid on;
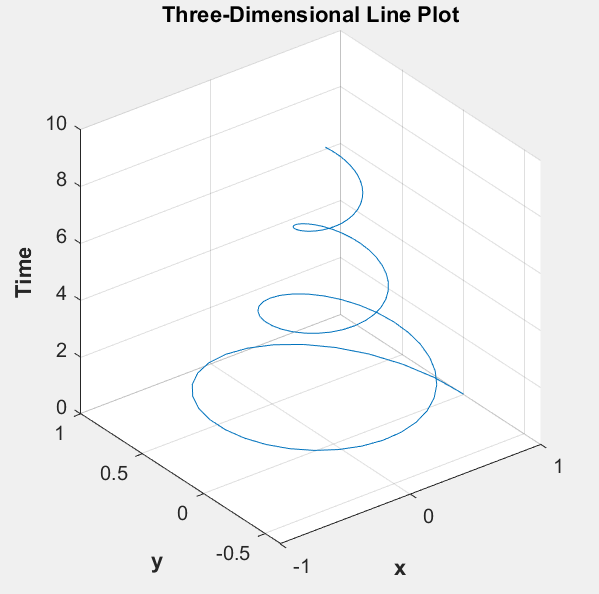
6.5.2 三维表面,网格,等高线图象

三维网格:
[x,y] = meshgrid(-4:0.2:4,-4:0.2:4);
z = exp(-0.5*(x.^2+y.^2));
mesh(x,y,z);
xlabel('\bfx');
ylabel('\bfy');
zlabel('\bfz');
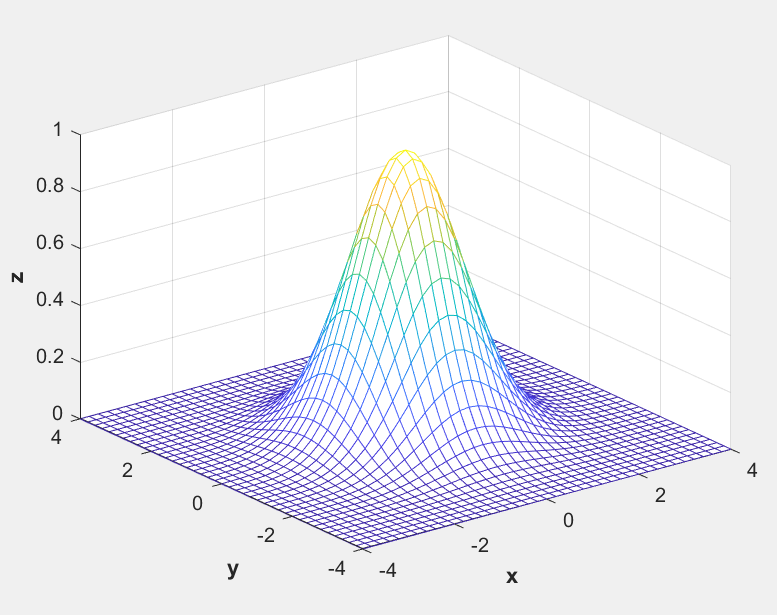
三维表面:
[x,y] = meshgrid(-4:0.2:4,-4:0.2:4);
z = exp(-0.5*(x.^2+y.^2));
surf(x,y,z);
xlabel('\bfx');
ylabel('\bfy');
zlabel('\bfz');
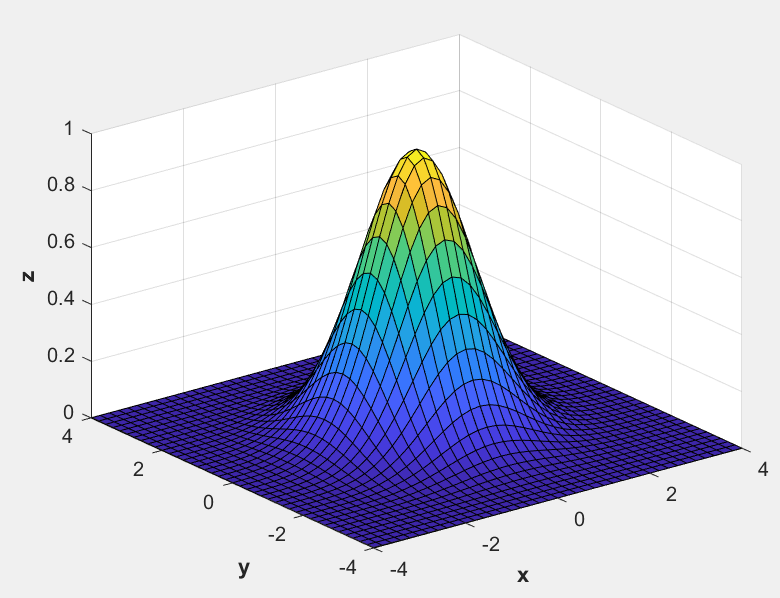
三维等高线:
[x,y] = meshgrid(-4:0.2:4,-4:0.2:4);
z = exp(-0.5*(x.^2+y.^2));
contour(x,y,z);
xlabel('\bfx');
ylabel('\bfy');
zlabel('\bfz');
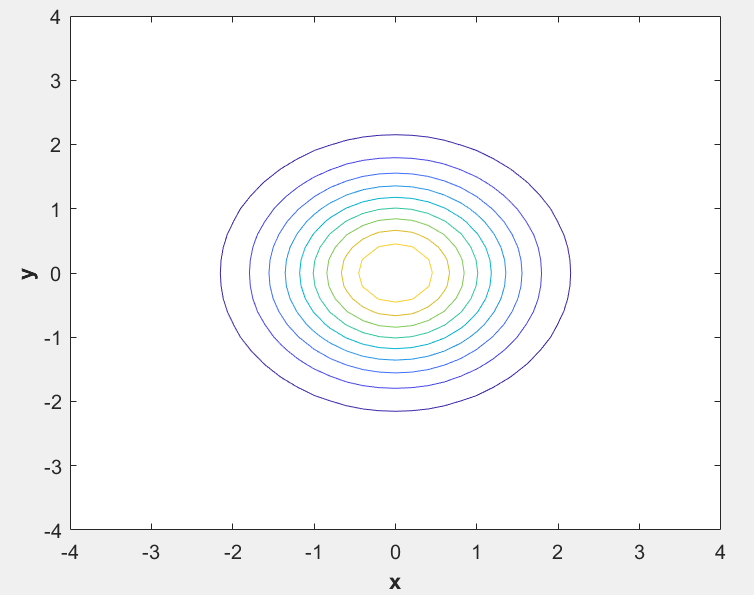
6.6 总结

相关文章:

MATLAB系列06:复数数据、字符数据和附加画图类
MATLAB系列06:复数数据、字符数据和附加画图类 6. 复数数据、字符数据和附加画图类6.1 复数数据6.1.1 复变量( complex variables)6.1.2 带有关系运算符的复数的应用6.1.3 复函数( complex function)6.1.4 复数数据的作…...

【永磁同步电机(PMSM)】 4. 同步旋转坐标系仿真模型
【永磁同步电机(PMSM)】 4. 同步旋转坐标系仿真模型 1. Clarke 变换的模型与仿真1.1 Clarke 变换1.2 Clarke 变换的仿真模型 2. Park 变换的模型与仿真2.1 Park 变换2.2 Park 变换的仿真模型 3. Simscape标准库变换模块3.1 abc to Alpha-Beta-Zero 模块3…...

CSAPP Attack Lab
个人感觉非常有意思的一个 Lab,涉及的知识面比较窄,主要关注 缓冲区溢出漏洞 这一个方面,并基于此进行代码攻击,体验一把做黑客的感觉,对应知识点为书中的 3.10 节内容。 这个 Lab 上手便给了我当头一棒,在…...

通信工程学习:什么是NFVI网络功能虚拟化基础设施层
NFVI:网络功能虚拟化基础设施层 NFVI(Network Functions Virtualization Infrastructure)即网络功能虚拟化基础设施层,是NFV(Network Functions Virtualization,网络功能虚拟化)架构中的一个重要…...

不在同一局域网怎么远程桌面?非局域网环境下,实现远程桌面访问的5个方法分享!
非局域网环境下,怎么远程桌面?还能做到吗? 在企业管理中,远程桌面访问已成为提高工作效率、实现跨地域协同工作的关键工具。 然而,当被控端与控制端不在同一局域网时,如何实现远程桌面连接成为了许多企业…...

SparkSQL-初识
一、概览 Spark SQL and DataFrames - Spark 3.5.2 Documentation 我们先看下官网的描述: SparkSQL是用于结构化数据处理的Spark模块,与基本的Spark RDD API不同。Spark SQL提供的接口为Spark提供了更多关于正在执行的数据和计算结构的信息。在内部&a…...
机制的迭代和优化历史)
Go语言的垃圾回收(GC)机制的迭代和优化历史
Go语言的垃圾回收(GC)机制自Go语言发布以来经历了多次重要的迭代和优化,以提高性能和减少程序运行时的停顿时间。 以下是一些关键的版本和相应的GC优化: Go版本GC耗时情况主要改进点Go 1.0-1.4可能达到几百毫秒至秒级使用简单的标…...

thinkphp8 从入门到放弃(后面会完善用到哪里写到哪)
thinkphp8 从入门到放弃 引言 thinkphp* 大道至简一、 thinkphp8 安装安装Composerthinkphp 安装命令(tp-项目名称)多应用安装(一个项目不会只有一个应用)安装完文件目录如下本地部署配置伪静态好了项目可以run 二、架构服务(Service…...

对于电商跨境电商独立站中源代码建站和SaaS建站的区别
电商跨境电商独立站的搭建有多种方式,作为电商企业,搭建完全自主控制的电商独立站,对于电商企业的发展和运营有着至关重要的作用。下面推荐一个使用多年的跨境电商独立站系统源码,做简要介绍,据说前段时间火爆的Pandab…...
使用vite+react+ts+Ant Design开发后台管理项目(二)
前言 本文将引导开发者从零基础开始,运用vite、react、react-router、react-redux、Ant Design、less、tailwindcss、axios等前沿技术栈,构建一个高效、响应式的后台管理系统。通过详细的步骤和实践指导,文章旨在为开发者揭示如何利用这些技术…...

C++之 string(中)
C之 string string类对象的容量操作 resize 将有效字符的个数该成n个,多出的空间用字符c填充 虽然在string里用的不多,但是在vector里面常见 这里有三种情况: 1)resize小于当前的size 2)resize大于当前的size,小于capacity …...

双向链表的基本结构及功能实现
1.基本结构: 双向链表是一种链表数据结构,它由一系列节点组成,每个节点包含三个部分: (1).数据域:存储节点的数据 (2).前驱指针:指向前一个节点 (3).后驱指针:指向下一个节点 2.基本特性: 双向链接: 与单向链表…...

stm32定时触发软件中断
这里使用定时器作为延时,单位为秒,使用exti的软件触发方式,配置见代码,在main里进行触发软件中断 代码 #include "stm32f10x.h" #include "stm32f10x_gpio.h" #include "misc.h" #include "…...

blender设置背景图怎么添加?blender云渲染选择
Blender是一款功能强大的3D建模软件,它以流畅的操作体验和直观的用户界面而闻名。使用Blender,你可以轻松地为你的3D模型添加背景图片。 以下是具体的操作步骤: 1、启动Blender:首先,打开Blender软件。访问添加菜单&a…...

MMD模型及动作一键完美导入UE5-Blender方案(三)
1、下载并安装blender_mmd_tools插件 1、下载并安装Blender,Blender,下载Blender3.6,下载太新的版本可能会跟blender_mmd_tools不匹配 2、github下载blender_mmd_tools:https://github.com/UuuNyaa/blender_mmd_tools/ 3、Edit->Preference->Add ons->Install F…...
网络安全自学入门:(超详细)从入门到精通学习路线规划,学完即可就业
很多人上来就说想学习黑客,但是连方向都没搞清楚就开始学习,最终也只是会无疾而终!黑客是一个大的概念,里面包含了许多方向,不同的方向需要学习的内容也不一样。 算上从学校开始学习,已经在网安这条路上走…...
如何在O2OA中使用ElementUI组件进行审批流程工作表单设计
本文主要介绍如何在O2OA中进行审批流程表单或者工作流表单设计,O2OA主要采用拖拽可视化开发的方式完成流程表单的设计和配置,不需要过多的代码编写,业务人员可以直接进行修改操作。 在流程表单设计界面,可以在左边的工具栏找到Ele…...
三、LLM应用开发准备工作
LLM应用开发准备工作 开发基础开发工具大模型kxswkey的配置与使用工具推荐结语 开发基础 最好具备一定的Python开发基础,不需要特别深 如果不具备,可以先学习一下基础知识(概念),比如Python环境管理、包管理与使用、基…...

机器学习-可解释性机器学习:随机森林与fastshap的可视化模型解析
可解释性机器学习是指使机器学习模型的决策过程透明化,帮助用户理解模型如何得出特定结果。随机森林和 FastSHAP 是常用的工具,以下是对它们的简要解析和可视化方法。 随机森林 1. 概述 随机森林是一种集成学习方法,通过构建多个决策树并结…...

使用Assimp加载glb/gltf文件,然后使用Qt3D来渲染
文章目录 1.代码2.说明2.1.调用2.2.关于贴图 1.代码 ModelLoader.h #ifndef MODELLOADER_H #define MODELLOADER_H#include <QObject> #include <Qt3DRender> #include <QVector3D> #include <QGeometry>#include <assimp/Importer.hpp> #incl…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
