随想录Day42--动态规划: 416. 分割等和子集(终于吃下01背包了)
今天只有1道题,属于动态规划的01背包问题的应用。首先理解一下动态规划的01背包问题。推荐一个视频,动态规划DP0-1背包,这是我认为讲得最为通透的。很多讲解动态背包问题的,一上来就画二维表格,遍历背包或者遍历容量,其实本质上,根本就看不懂那个二维表格是什么意思,为什么容量每次都要从0开始遍历。从原理上讲,容量从0开始只是一种假设,为的是让后面的背包如果装东西了,那么背包容量就会减少,再减少了容量后,怎么挑选物品才会使得质量最高,因此需要从0遍历,这些都是起了给后面的递归初始化一个值的作用。
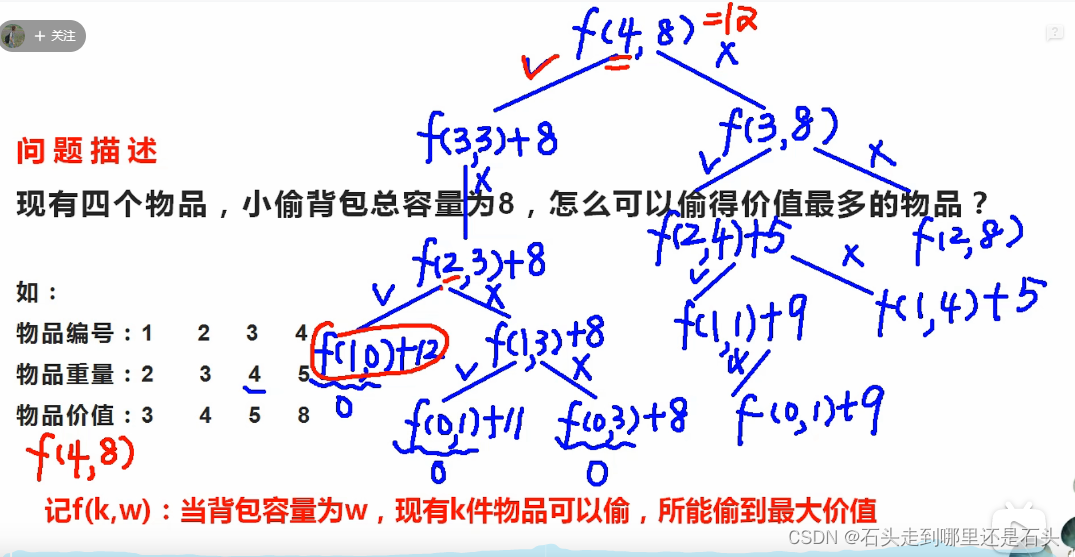
小偷偷东西,有一个8容量背包,那么他开始从编号4开始偷(也可以从编号1开始偷),他有两种选择,偷或者不偷。如果偷,那么它的背包剩余容量就是8 - 5 = 3;同时产生价值8,如果不偷,则背包容量为8,产生价值为0;接着开始偷第二件物品,也就是编号3,又是一个选择偷与不偷的过程。最后就会生成一棵二叉树,每个叶子节点都是不同选择下的结果,选择最大的叶子节点就是得到最大的价值。

因此就会产生一个状态转移方程,这个状态转移方程就是一种决策,如果背包容量不够,也就是物品太重,那么它产生的价值就是上次物品决策时的价值,也就是f(k - 1,w),同时剩余容量为w,也就背包的容量没有改变。如果背包容量足够,那么他就面临两种选择,偷和不偷,如果不偷,产生的价值不变,容量不变,如果偷,那么它的总价值就加上这个物品的价值,同时背包容量就相应减少。这时可以看到,背包容量减少后,对应的一个小背包容量,面临的选择是剩下两个物品的决策。这时对应的背包容量和剩下物品中对应获取的最大值在前面的遍历已经有给出了,所以查表就可以得到对应的最大值,也就是这种决策下的产生的最大价值。
其实在引申下去,就是从只有1个物品和只有有限背包容量时,能产生的最大价值。接着有两个物品和有限背包容量时的选择,选择第2个物品后,就回头看剩下的背包容量以及只有1个物品时对应的价值,返回不选择第二件物品和选择了第二件物品的价值的最大值。也就是状态转移方程中的第wk<= w的情况。

最终的f(4,8)就是我们决策的结果,其余的表格数字只是一个铺垫,都是每个决策产生的最大值,但是最后的f(4,8)才是我们有4个物品,同时背包容量为8的结果。所以里面的关系要搞清楚,表格的其他数字都和我们01背包的题目没有关系,但是它是一个重要的推导过程,他有点类似于遍历所有结果,把决策的结果反应在表格上。可能我讲得确实不够清楚,但是,强烈推荐看视频讲解,从原理上解剖背包问题和决策,真的可以深刻理解这个表格以及整个动态规划的核心。动态规划DP0-1背包。
力扣题目416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5] 输出:true 解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5] 输出:false 解释:数组不能分割成两个元素和相等的子集。
提示:
1 <= nums.length <= 2001 <= nums[i] <= 100
回到题目:分割等和子集,这个可以看成背包容量为整个集合的和的一半,只要背包正好装满,那么这个背包的价值就是整个集合的一半,背包的和与剩下的子集的和相等,可以返回true。因此在借用这个思想,遍历所有物品,也就是集合里面的元素,从只有1个元素可以选择到所有的元素都可以选择,在这个过程中,只要找到背包满的情况,就能输出true,因为只要选择了这些元素就可以了。
class Solution {public boolean canPartition(int[] nums) {int sum = 0;for(int num : nums){sum += num;}if(sum % 2 == 1 || nums.length == 1){return false;}int[][] dp = new int[nums.length][sum / 2 + 1];for(int i = 0; i < nums.length; i++){dp[i][0] = 0;}for(int j = 0; j <= sum / 2; j++){if(j >= nums[0]){dp[0][j] = nums[0];}}for(int i = 1; i < nums.length; i++){for(int j = 1; j <= sum / 2; j++){if(j >= nums[i]){dp[i][j] = Math.max(dp[i - 1][j] ,dp[i - 1][j - nums[i]] + nums[i]);}else{dp[i][j] = dp[i - 1][j];}}//这一步是关键,因为不知道选多少个元素,所以每次添加一个元素进行选择时,就判断一次//正好满足条件就可以返回true,否则就再加一个元素,直到加到没有元素可以加后结束遍历返回falseif(dp[i][sum / 2] == sum / 2){return true;}}// for (int i = 0; i < nums.length; i++) {// for (int j = 0; j <= sum / 2; j++) {// System.out.print(dp[i][j]+" ");// }// System.out.println();// }return false;}}终于把01背包吃下了,不容易呀!!!
相关文章:

随想录Day42--动态规划: 416. 分割等和子集(终于吃下01背包了)
今天只有1道题,属于动态规划的01背包问题的应用。首先理解一下动态规划的01背包问题。推荐一个视频,动态规划DP0-1背包,这是我认为讲得最为通透的。很多讲解动态背包问题的,一上来就画二维表格,遍历背包或者遍历容量&a…...
字节跳动软件测试岗,前两面过了,第三面被面试官吊打,结局我哭了
阎王易见,小鬼难缠。我一直相信这个世界上好人居多,但是也没想到自己也会在阴沟里翻船。我感觉自己被字节跳动的HR坑了。 在这里,我只想告诫大家,offer一定要拿到自己的手里才是真的,口头offer都是不牢靠的࿰…...

bitlocker 笔记
介绍 bitlocker是windows自带的磁盘加密工具,win10专业版是可以使用的,其他家庭版本可能没有这个功能。有点类似与wd security。 功能 加密磁盘,当磁盘物理丢失时,防止磁盘中的数据泄露。举个例子,移动硬盘被偷&…...

Linux 压缩与解压命令
一、常见的压缩文件扩展名 1、*.Z compress程序压缩的文件 2、*.gz gzip程序压缩的文件 3、.tar.gz tar程序打包的文件,其中经过gzip的压缩 4、.tar tar程序打包的数据,并没有压缩过 5、.bz2 bzip2程序压缩的文件 6、.tar.bz2 tar程序打包的文件&a…...

python global函数用法及常用的 global函数代码
Python中的 global函数是用于在程序中定义变量的函数,在我们实际的开发中,我们可能会用到 global函数来定义变量,但是我们在这里就不具体介绍它的用法了。 global函数定义变量的方法: global函数使用参数a来指定变量在程序中的地址…...

大数据学完好就业么
Python的普及与数据挖掘、人工智能和数值计算等领域的蓬勃发展相关,但同时也与普遍编程需求的增加有关。 Python应用领域广泛,意味着选择Python的同学在学成之后可选择的就业领域有很多,加上Python本身的优势,致使现在越来越多的…...
CASAtomic 原子操作详解
文章目录CAS&Atomic 原子操作详解什么是原子操作CAS相关原子操作类的使用AtomicIntegerAtomicIntegerArray更新引用类型原子更新字段类LongAdderCAS&Atomic 原子操作详解 什么是原子操作 Mysql事务中的原子性就是一个事务中执行的多条sql,要么同时成功&am…...
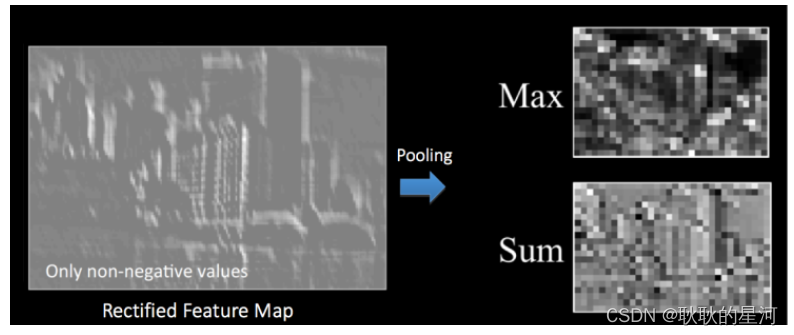
卷积神经网络(convolutional neural network, CNN)
卷积神经网络(convolutional neural network, CNN) 卷积神经网络(convolutional neural network, CNN),是一种专门用来处理具有类似网格结构的数据的神经网络。卷积网络是指那些至少在网络的一层中使用卷积运算来替代…...
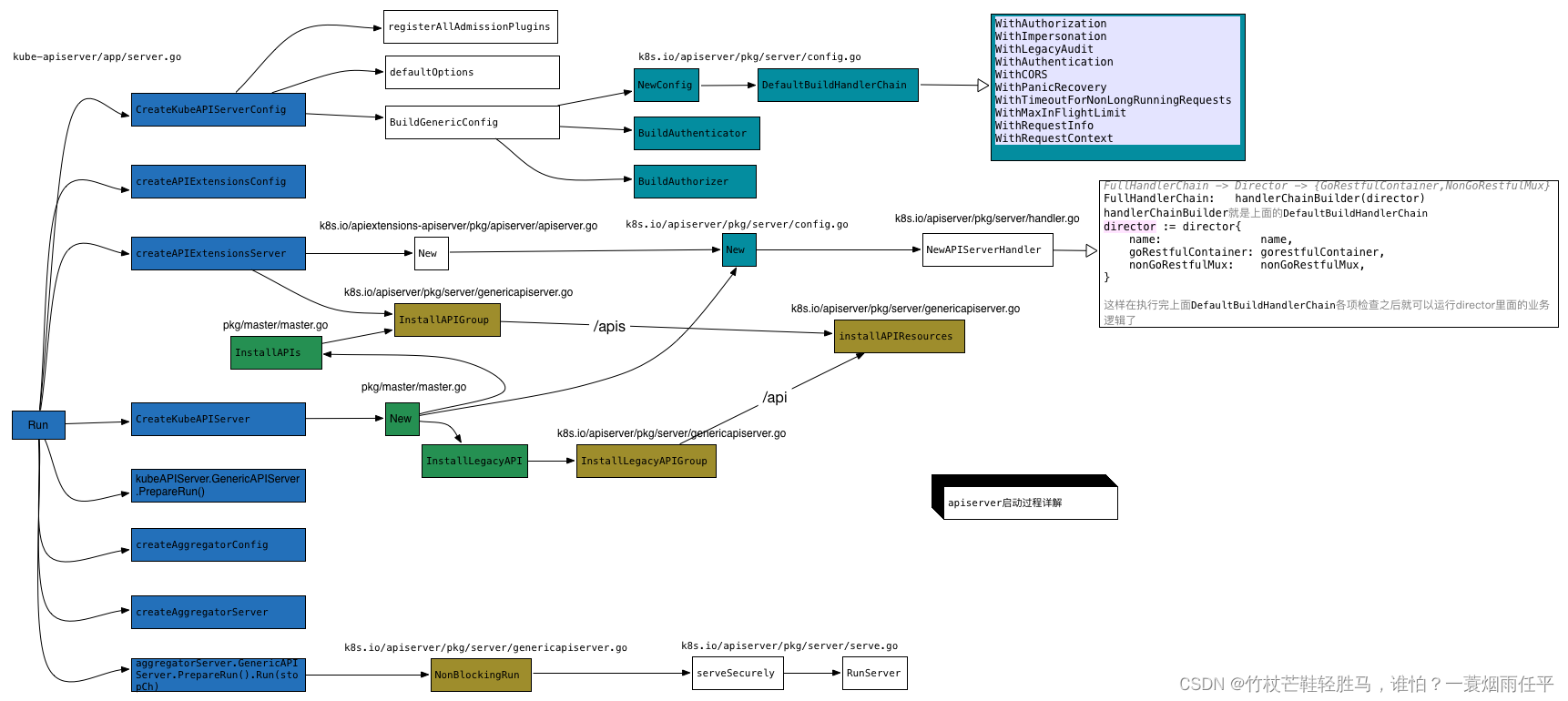
kube-apiserver启动流程源码分析
1. 概述 KubeAPIServer 主要是提供对 API Resource 的操作请求,为 kubernetes 中众多 API 注册路由信息,暴露 RESTful API 并且对外提供 kubernetes service,使集群中以及集群外的服务都可以通过 RESTful API 操作 kubernetes 中的资源。 2…...
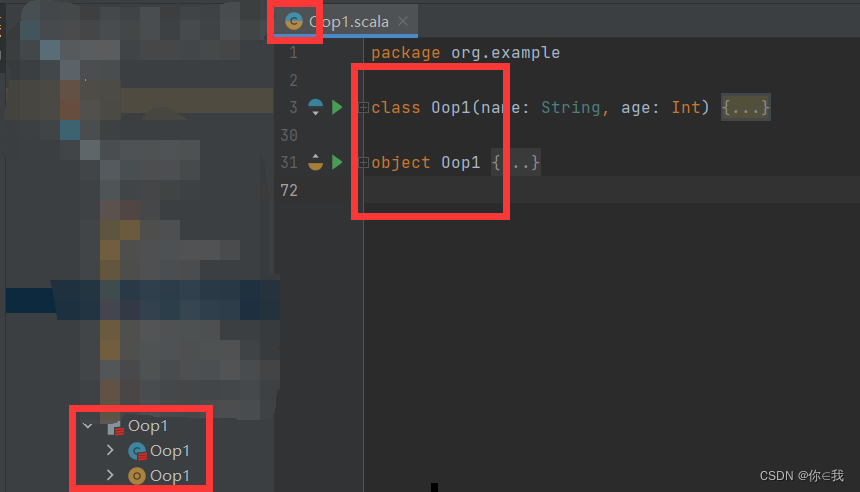
Scala基础(二)
单例对象(object) Scala的类中无法定义静态成员,即无static关键字。如何像Java一样表达类的静态成员变量、成员方法与静态代码块? Scala解决方案:单例对象 使用“object”关键字声明,可包含变量、方法与…...

Python 生产者消费者模型是什么?
本文首发自「慕课网」,想了解更多IT干货内容,程序员圈内热闻,欢迎关注! 作者| 慕课网精英讲师 朱广蔚 1. 简介 生产者和消费者问题是线程模型中的经典问题: 生产者和消费者共享同一个存储空间生产者往存储空间中添…...
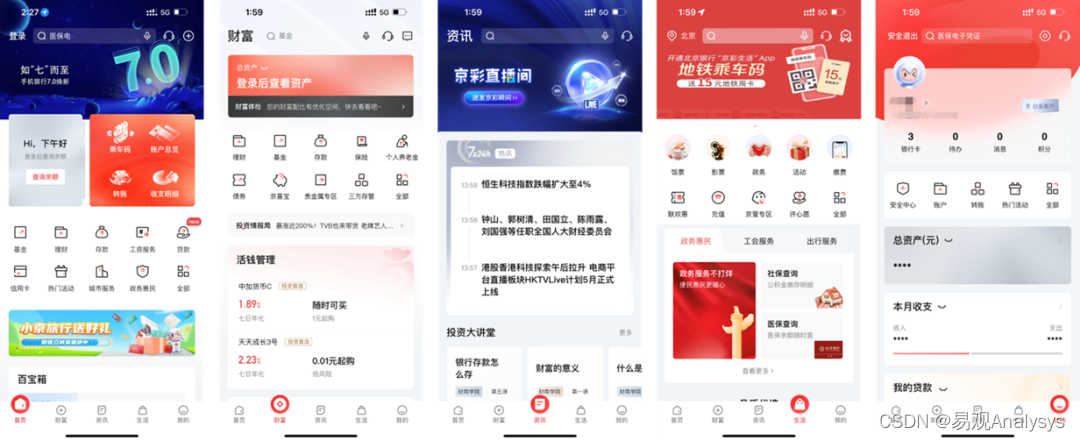
手机银行评测系列:北京银行“京彩生活”7.0从用户视角出发,实现沉浸式体验重塑
易观:2023年3月28日,北京银行发布“京彩生活”APP 7.0版本,从旅程再造、特色金融、场景生态、平台联动、协同经营、体验管理和安全守护七大方面全面升级,从用户视角出发,重塑用户旅程,简化操作流程…...

ZJYC2023 浙江省大学生程序设计竞赛校内选拔赛部分题解 C J B L
ZJYC2023 浙江省大学生程序设计竞赛校内选拔赛部分题解 C J B L 难度分布: 签到:CJ Easy:BL Midium:IAGKFE Hard:DH 题解: 签到:CJ C - ^{-1} 参考代码: #include<bits/std…...

百科创建:7种有效的百科词条创建技巧
百科词条是互联网上最常见的知识信息资源之一,它们是人们查找信息的主要途径之一。创建一个高质量的百科词条并不是一件容易的事情,需要一些技巧和经验才能做到。下面是一些创建百科词条的技巧: 一、确保词条的独特性 在创建百科词条之前&…...
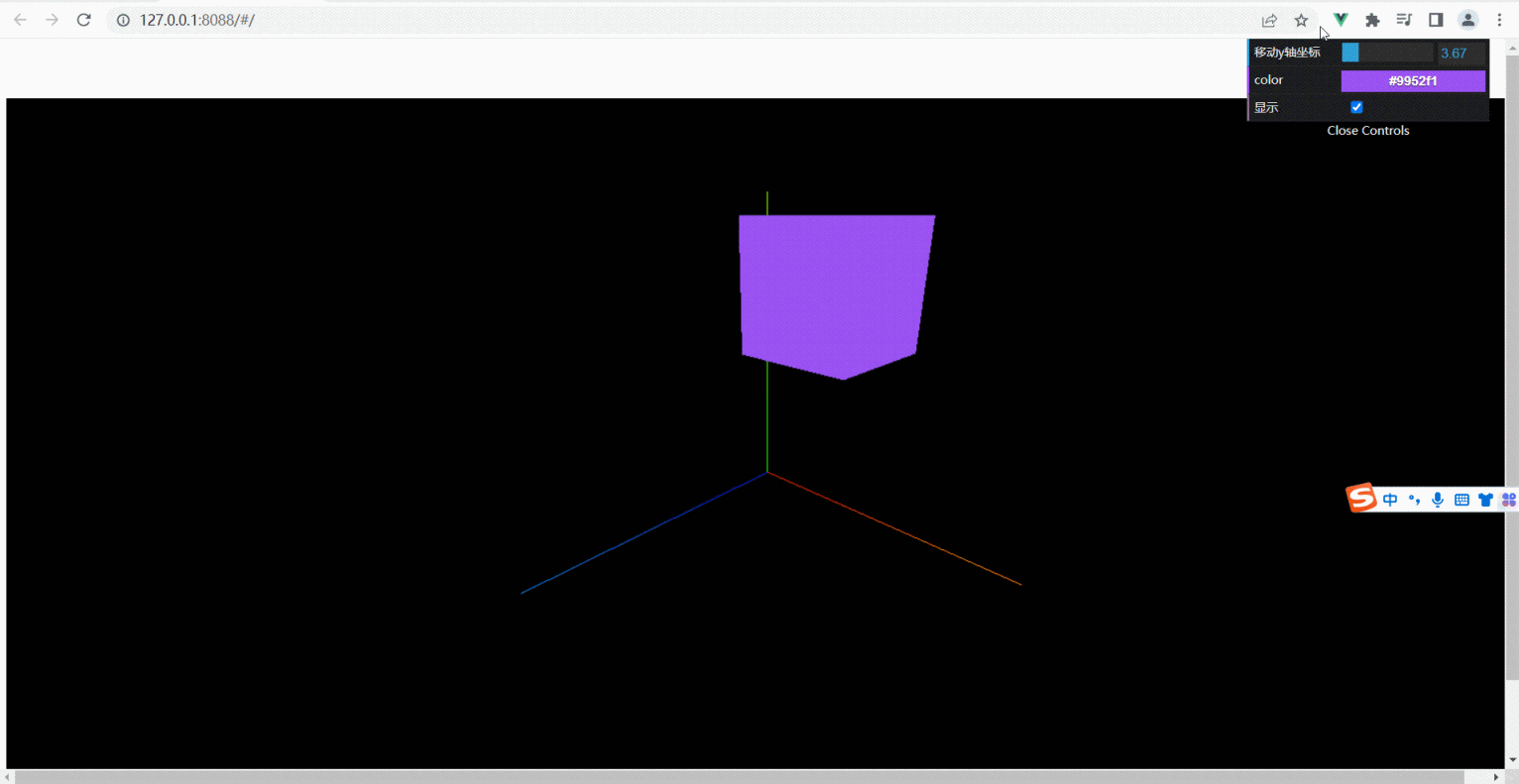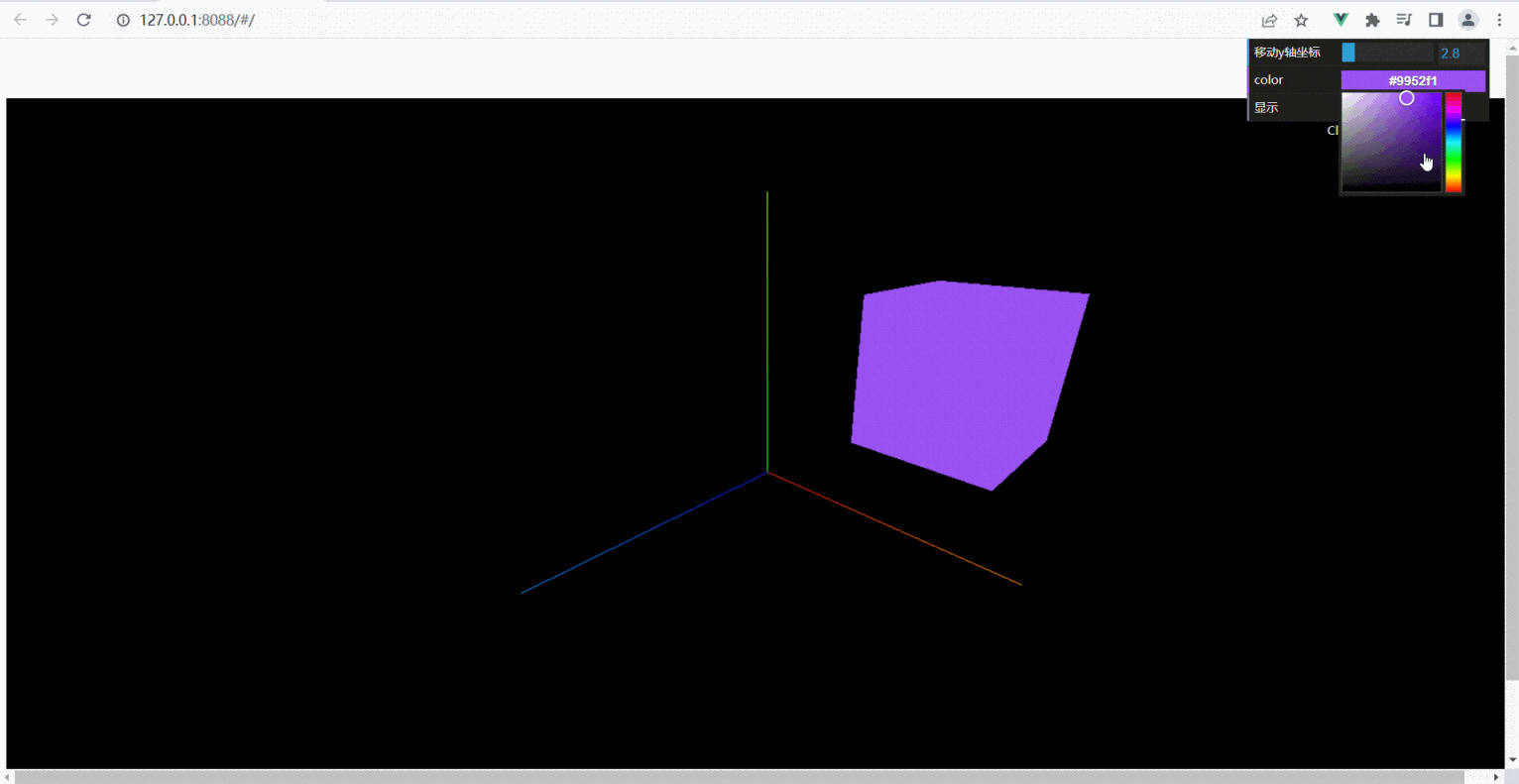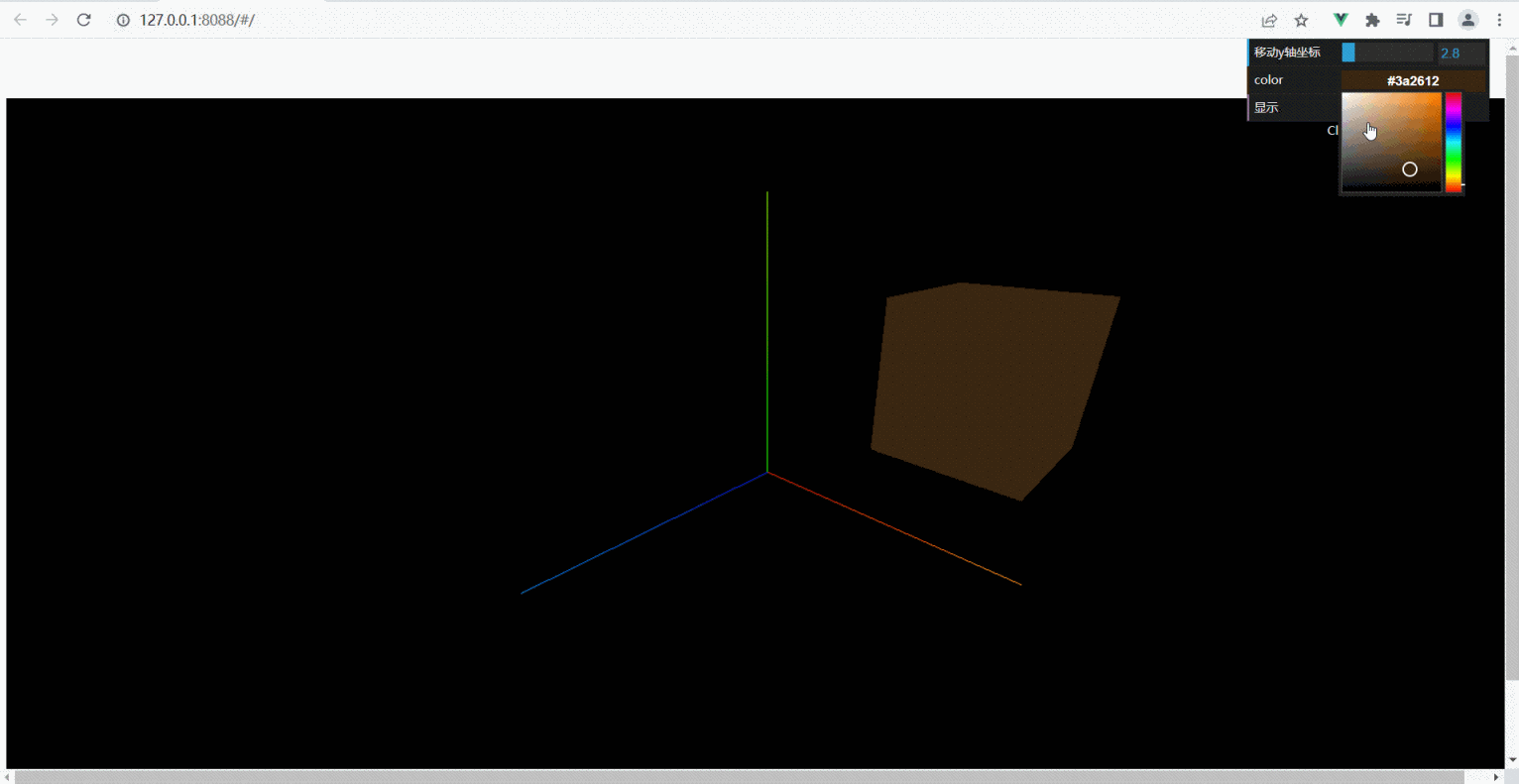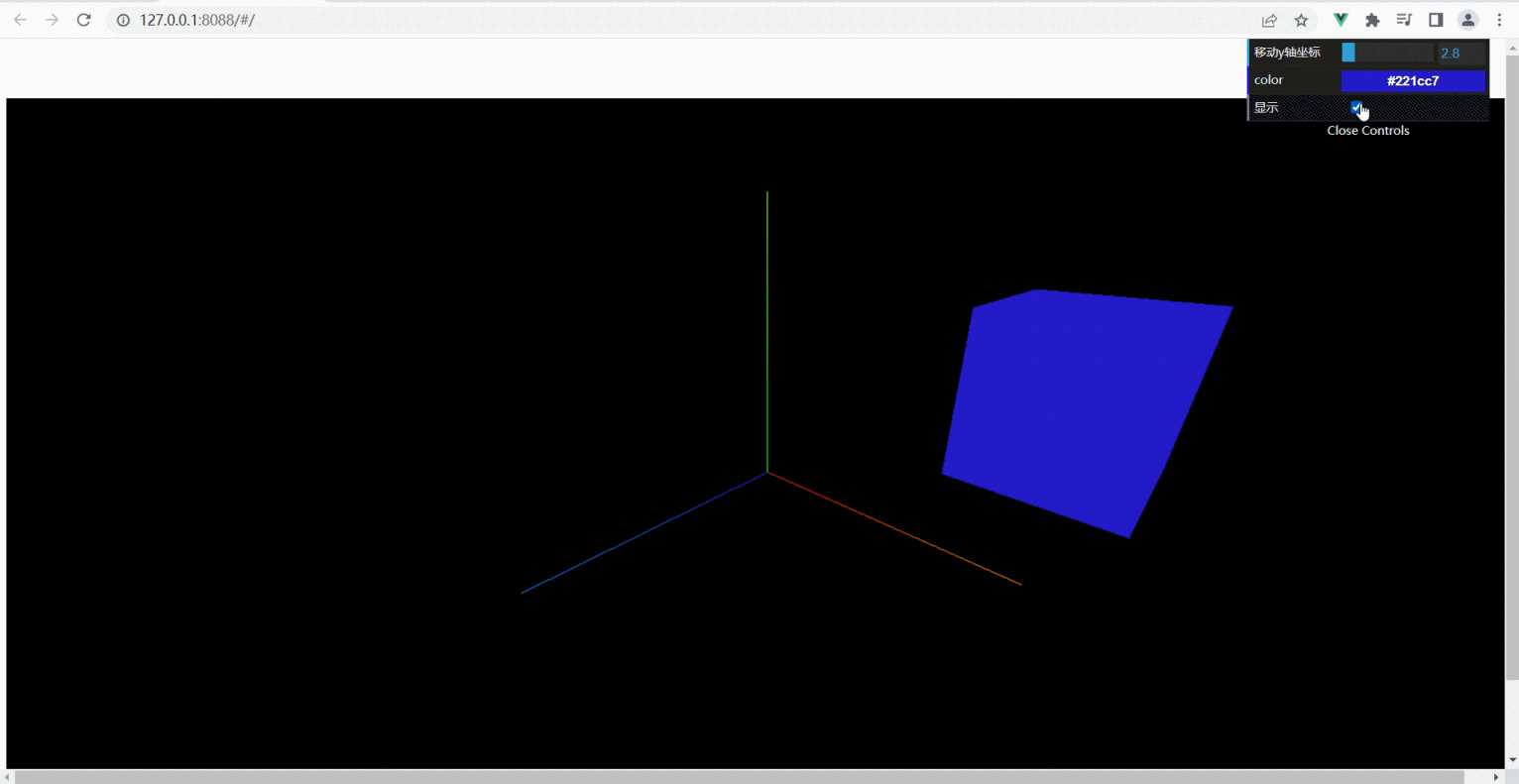
ThreeJS-dat.gui界面控制颜色、隐藏、位置(六)
下载组件dat.gui npm install dat.gui -S 引入组件 import * as dat from dat.gui //界面控制 代码: <template> <div id"three_div"> </div> </template> <script> import * as THREE from "three"; import {O…...
接口自动化测试,完整入门篇
目录 1. 什么是接口测试2. 基本流程3. 需求分析4. 用例设计5. 脚本开发6. 结果分析7. 完整脚本8. 参考资料1. 什么是接口测试 顾名思义,接口测试是对系统或组件之间的接口进行测试,主要是校验数据的交换,传递和控制管理过程,以及…...

利用ControlNet重新定义你的AI姿势
利用ControlNet重新定义你的AI姿势 前段时间给大家分享了如何利用colab实现AI绘画自由,现在Stable Diffusion WebUI Colab TW又更新了不少新功能。最重要的是可以通过谷歌硬盘的快捷方式导入模型,极大的节省了谷歌硬盘容量。 众所周知,谷歌…...
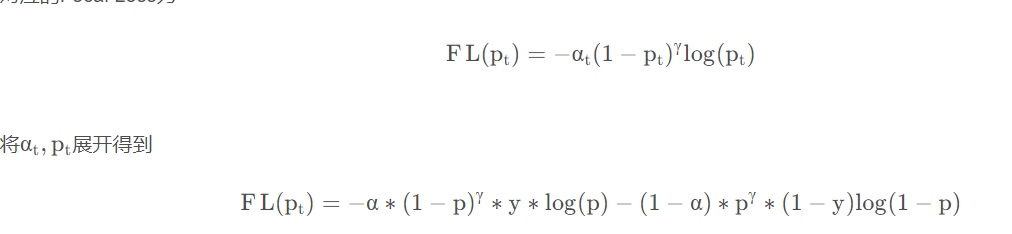
中医药NER命名实体识别基于SPANNER方式
一个不知名大学生,江湖人称菜狗 original author: Jacky Li Email : 3435673055qq.com Time of completion:2023.3.5 Last edited: 2023.3.5 导读 本文使用SPANNER方式实现对中医药进行实体识别,采用focal loss 进行优化。 本文章作用防止安静…...

Vue必掌握
目录 一、组件通信方式 二、v-if和v-for 三、生命周期 1、描述 2、setup和created谁先执行 3、setup中为什么没有beforeCreate和created 四、双向绑定 v-model 1、定义 2、本质,原理 3、好处 五、如何扩展一个组件 1、mixins 缺点 2、slot插槽 3、e…...

SSM部分
声明式事务 从之前的事务控制的代码中可以看出,是有规律可循,代码的结构基本是确定的,所以框架就可以将固定模式的代码抽取出来,进行相关的封装。 封装起来后,我们只需要在配置文件中进行简单的配置即可完成操作。 …...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...
