学习Tensorflow之基本操作
学习Tensorflow之基本操作
- Tensorflow基本操作
- 1. 创建张量
- (1) 创建标量
- (2) 创建向量
- (3) 创建矩阵
- (4) shape属性
- (5) 判别张量类型
- (6) 列表和ndarray转张量
- 2. 创建特殊张量
- (1) tf.ones与tf.ones_like
- (2) tf.zeros与tf.zeros_like
- (3) tf.fill
- (3) tf.random.normal
- (4) tf.random.uniform
- 3. 张量的运算
- (1) 四则运算
- (2) 绝对值、乘方、开平方
- (3) 矩阵乘法
- (4) tf.cast
- (5) 张量的索引与切片
- (6) tf.reshape
- (7) 增加和减少张量的维度
- (8) 维度交换
- 4. 字符串张量
- (1) 转为字符串张量
- (2) 字符串分割
- (3) 字符串拼接
- (3) 字符串大小写转换
- 5. 不规则张量
- (1) 创建不规则张量
- (2) 不规则张量的运算
- (3) 不规则张量的数学变换
Tensorflow基本操作
1. 创建张量
创建张量的函数为
tensorflow.constant(value, 值dtype = None, 类型(默认为32位)shape = None, 形状name = 'Const' 名称
)
(1) 创建标量
import tensorflow as tfscalarInt = tf.constant(2)
scalarFloat = tf.constant(3.0)
scalarString = tf.constant('Hello')print(scalarInt)
print(scalarFloat)
print(scalarString)
tf.Tensor(2, shape=(), dtype=int32)
tf.Tensor(3.0, shape=(), dtype=float32)
tf.Tensor(b’Hello’, shape=(), dtype=string)
从结果可以看出,标量的维度是0,所以shape值为空
(2) 创建向量
import tensorflow as tfvectorInt = tf.constant([2])
vectorFloat = tf.constant([3.0, 4.0])
vectorString = tf.constant(['Hello', 'World'])print(vectorInt)
print(vectorFloat)
print(vectorString)
tf.Tensor([2], shape=(1,), dtype=int32)
tf.Tensor([3. 4.], shape=(2,), dtype=float32)
tf.Tensor([b’Hello’ b’World’], shape=(2,), dtype=string)
向量的创建必须加上[],将他作为列表传入函数,方括号的个数代表着tensor的维度
(3) 创建矩阵
import tensorflow as tfmatrixInt = tf.constant([[2], [3]])
matrixFloat = tf.constant([[3.0, 4.0]])
matrixString = tf.constant([['Hello'], ['World']])print(matrixInt)
print(matrixFloat)
print(matrixString)
tf.Tensor(
[[2][3]], shape=(2, 1), dtype=int32)
tf.Tensor([[3. 4.]], shape=(1, 2), dtype=float32)
tf.Tensor(
[[b'Hello'][b'World']], shape=(2, 1), dtype=string)
(4) shape属性
shape属性记录着tensor的形状
| shape的取值 | 含义 |
|---|---|
| () | 该tensor是标量 |
| (列数, ) | 该tensor是向量 |
| (行数, 列数) | 该tensor是矩阵 |
| (层数, 行数, 列数) | 该tensor是数据立方体 |
(5) 判别张量类型
使用tf.rank()函数可以判别张量的类型
import tensorflow as tfscalarInt = tf.constant(5)
vectorFloat = tf.constant([3.0, 4.0])
matrixString = tf.constant([['Hello'], ['World']])print(tf.rank(scalarInt))
print(tf.rank(vectorFloat))
print(tf.rank(matrixString))
tf.Tensor(0, shape=(), dtype=int32)
tf.Tensor(1, shape=(), dtype=int32)
tf.Tensor(2, shape=(), dtype=int32)
这里的0、1、2代表的是tensor的维度
(6) 列表和ndarray转张量
tensorflow.convert_to_tensor(value, 值dtype = None, 类型(默认为32位)
)
import numpy as np
import tensorflow as tfl = [1, 2, 3]
array = np.array([1.0, 2.2])print(tf.convert_to_tensor(l))
print(tf.convert_to_tensor(array))
tf.Tensor([1 2 3], shape=(3,), dtype=int32)
tf.Tensor([1. 2.2], shape=(2,), dtype=float32)
2. 创建特殊张量
| 方法 | 作用 |
|---|---|
tf.ones(shape, dtype, name) | 创建全1的张量 |
tf.ones_like(input, dtype, name) | 创建全1的张量,包含所有与输入相同的形状 |
tf.zeros(shape, dtype, name) | 创建全0的张量 |
tf.zeros_like(input, dtype, name) | 创建全0的张量,包含所有与输入相同的形状 |
tf.fill(dims, value, name) | 创建值全相同的张量 |
tf.random.normal(shape, mean, stddev, dtype, seed, name) | 创建正态分布的张量 |
tf.random.uniform(shape, minval, maxval, dtype, seed, name) | 创建平均分布的张量 |
tf.random.poisson(shape, lam, dtype, seed, name) | 创建泊松分布的张量 |
tf.random.gamma(shape, alpha, beta, dtype, seed, name) | 创建伽马分布的张量 |
(1) tf.ones与tf.ones_like
import tensorflow as tfones = tf.ones((3, 3))
scalarInt = tf.constant(1)
print(ones)ones_like = tf.ones_like(scalarInt, dtype = tf.float32, name = 'ones_like')
print(ones_like)
tf.Tensor(
[[1. 1. 1.][1. 1. 1.][1. 1. 1.]], shape=(3, 3), dtype=float32)
tf.Tensor(1.0, shape=(), dtype=float32)
(2) tf.zeros与tf.zeros_like
import tensorflow as tfzeros = tf.zeros((3, 3))
scalarInt = tf.constant(1)
print(zeros)zeros_like = tf.zeros_like(scalarInt, dtype = tf.string, name = 'zeros_like')
print(zeros_like)
tf.Tensor(
[[0. 0. 0.][0. 0. 0.][0. 0. 0.]], shape=(3, 3), dtype=float32)
tf.Tensor(b'', shape=(), dtype=string)
从结果可以看出,对于字符串类型,0表示的空字符串
(3) tf.fill
import tensorflow as tffiveInt = tf.fill((3, 3), 5)
fiveString = tf.fill((3, 3), '5')
print(fiveInt)
print(fiveString)
tf.Tensor(
[[5 5 5][5 5 5][5 5 5]], shape=(3, 3), dtype=int32)
tf.Tensor(
[[b'5' b'5' b'5'][b'5' b'5' b'5'][b'5' b'5' b'5']], shape=(3, 3), dtype=string)
tf.fill()函数没有dtype参数,系统通过传入value的值来自动判断张量的类型
(3) tf.random.normal
import tensorflow as tfnormal = tf.random.normal((2, 2), 0.0, 1.0, tf.float16)
print(normal)
tf.Tensor(
[[-0.919 1.498][ 0.896 -2.05 ]], shape=(2, 2), dtype=float16)
默认情况下,创建的类型是tf.float32
(4) tf.random.uniform
import tensorflow as tfuniform = tf.random.uniform((2, 2), 0.0, 10.0, tf.float16)
print(uniform)
tf.Tensor(
[[2.09 2.812][2.822 6.21 ]], shape=(2, 2), dtype=float16)
默认情况下,创建的类型是tf.float32
3. 张量的运算
| 方法 | 作用 |
|---|---|
tf.add(x, y, name) 或 运算符 + | 计算张量相加 |
tf.subtract(x, y, name) 或 运算符 - | 计算张量相减 |
tf.multiply(x, y, name) 或 运算符 * | 计算张量相乘 |
tf.divide(x, y, name) 或 运算符 / | 计算张量相除 |
tf.abs(x, name) | 计算张量绝对值 |
tf.pow(x, y, name) | 计算张量乘方 |
tf.sqrt(x, name) | 计算张量开平方 |
tf.matmul(a, b, transpose_a, transpose_b) 或 运算符@ | 计算矩阵乘法 |
tf.cast(x, dtype, name) | 强制类型转换 |
tensor[层数][行数][列数] | 张量索引 |
[start : end : step] | 张量切片 |
tf.reshape(tensor, shape, name) | 张量维度转换 |
tf.expand_dims(input, axis, name) | 增加张量的维度 |
tf.squeeze(input, axis, name) | 减少张量的维度 |
tf.transpose(a, perm, conjugate) | 交换张量的维度 |
(1) 四则运算
import tensorflow as tft1 = tf.constant([1, 2])
t2 = tf.constant([2, 4])
print(tf.add(t1, t2))
print(tf.subtract(t1, t2))
print(tf.multiply(t1, t2))
print(tf.divide(t1, t2))
print()
print(t1 + t2)
print(t1 - t2)
print(t1 * t2)
print(t1 / t2)
tf.Tensor([3 6], shape=(2,), dtype=int32)
tf.Tensor([-1 -2], shape=(2,), dtype=int32)
tf.Tensor([2 8], shape=(2,), dtype=int32)
tf.Tensor([0.5 0.5], shape=(2,), dtype=float64)tf.Tensor([3 6], shape=(2,), dtype=int32)
tf.Tensor([-1 -2], shape=(2,), dtype=int32)
tf.Tensor([2 8], shape=(2,), dtype=int32)
tf.Tensor([0.5 0.5], shape=(2,), dtype=float64)
(2) 绝对值、乘方、开平方
import tensorflow as tft1 = tf.constant([-1.0, 2])print(tf.abs(t1))
print(tf.pow(t1, 3))
print(tf.sqrt(t1))
tf.Tensor([1. 2.], shape=(2,), dtype=float32)
tf.Tensor([-1. 8.], shape=(2,), dtype=float32)
tf.Tensor([ nan 1.4142135], shape=(2,), dtype=float32)
-1不能开平方,所以计算结果是nan,即not a number
(3) 矩阵乘法
import tensorflow as tfa = tf.constant([1, 2], shape = (1, 2))
b = tf.constant([1, 2], shape = (2, 1))print(a)
print(b)
print(tf.matmul(a, b))
tf.Tensor([[1 2]], shape=(1, 2), dtype=int32)
tf.Tensor(
[[1][2]], shape=(2, 1), dtype=int32)
tf.Tensor([[5]], shape=(1, 1), dtype=int32)
注意:相乘的矩阵必须满足矩阵乘法的规则
设置转置参数
import tensorflow as tfa = tf.constant([[1, 2]])
b = tf.constant([[1, 2]])
print(a)
print(b)
print(tf.matmul(a, b, False, True))
tf.Tensor([[1 2]], shape=(1, 2), dtype=int32)
tf.Tensor([[1 2]], shape=(1, 2), dtype=int32)
tf.Tensor([[5]], shape=(1, 1), dtype=int32)
在tensorflow中,向量是不能与矩阵进行乘法运算的,我们在学习数学的时候,都把向量看成了1维矩阵,但是tensorflow中向量是向量,不是矩阵
import tensorflow as tfa = tf.constant([1, 2])
b = tf.constant([[2], [1]])
print(a)
print(b)
print(tf.matmul(a, b, False, True))
tf.Tensor([1 2], shape=(2,), dtype=int32)
tf.Tensor(
[[2][1]], shape=(2, 1), dtype=int32)
tensorflow.python.framework.errors_impl.InvalidArgumentError: {{function_node __wrapped__MatMul_device_/job:localhost/replica:0/task:0/device:CPU:0}} In[0] and In[1] has different ndims: [2] vs. [2,1] [Op:MatMul]
所以,在tensorflow中需要注意,向量和矩阵不能进行运算
(4) tf.cast
强制类型转换
import tensorflow as tfscalarInt = tf.constant(2)
scalarFloat = tf.cast(scalarInt, dtype = tf.float32)
print(scalarInt)
print(scalarFloat)
tf.Tensor(2, shape=(), dtype=int32)
tf.Tensor(2.0, shape=(), dtype=float32)
(5) 张量的索引与切片
按照维度:
3维:tensor[层][行][列]
2维:tensor[行][列]
1维:tensor[列]
import tensorflow as tft = tf.constant([i for i in range(25)], shape = (5, 5))
print(t)
# t为2维,取第二行
print(t[1])
# 取第一行第二列
print(t[0, 1])
tf.Tensor(
[[ 0 1 2 3 4][ 5 6 7 8 9][10 11 12 13 14][15 16 17 18 19][20 21 22 23 24]], shape=(5, 5), dtype=int32)
tf.Tensor([5 6 7 8 9], shape=(5,), dtype=int32)
tf.Tensor(1, shape=(), dtype=int32)
取某一维度的全部元素,使用:
import tensorflow as tft = tf.constant([i for i in range(25)], shape = (5, 5))
print(t)
# 取所有行第二列
print(t[:, 1])
# 取第二行第全部列,即第二行
print(t[3, :])
tf.Tensor(
[[ 0 1 2 3 4][ 5 6 7 8 9][10 11 12 13 14][15 16 17 18 19][20 21 22 23 24]], shape=(5, 5), dtype=int32)
tf.Tensor([ 1 6 11 16 21], shape=(5,), dtype=int32)
tf.Tensor([15 16 17 18 19], shape=(5,), dtype=int32)
按照间隔取:[start : end : step]
取的范围为 [start : end),即不会取到end
import tensorflow as tft = tf.constant([i for i in range(25)], shape = (5, 5))
print(t)print(t[0:5:2])
tf.Tensor(
[[ 0 1 2 3 4][ 5 6 7 8 9][10 11 12 13 14][15 16 17 18 19][20 21 22 23 24]], shape=(5, 5), dtype=int32)
tf.Tensor(
[[ 0 1 2 3 4][10 11 12 13 14][20 21 22 23 24]], shape=(3, 5), dtype=int32)(6) tf.reshape
张量维度转换
import tensorflow as tft = tf.constant([i for i in range(20)], shape = (4, 5))
print(t)t = tf.reshape(t, (2, 10))
print(t)
tf.Tensor(
[[ 0 1 2 3 4][ 5 6 7 8 9][10 11 12 13 14][15 16 17 18 19]], shape=(4, 5), dtype=int32)
tf.Tensor(
[[ 0 1 2 3 4 5 6 7 8 9][10 11 12 13 14 15 16 17 18 19]], shape=(2, 10), dtype=int32)
从结果可以看出4×5的矩阵转换成了2×10的矩阵
如果在reshape时,某一维度写-1,系统会自动计算出这个维度的值
import tensorflow as tft = tf.constant([i for i in range(20)], shape = (4, 5))
print(t)t = tf.reshape(t, (-1, 10))
print(t)
tf.Tensor(
[[ 0 1 2 3 4][ 5 6 7 8 9][10 11 12 13 14][15 16 17 18 19]], shape=(4, 5), dtype=int32)
tf.Tensor(
[[ 0 1 2 3 4 5 6 7 8 9][10 11 12 13 14 15 16 17 18 19]], shape=(2, 10), dtype=int32)
(4, 5) -> (-1, 10)可以理解为将4×5的矩阵转换成了若干行10列的矩阵
(7) 增加和减少张量的维度
使用tf.expand_dims()可以增加张量的维度
import tensorflow as tf# 增加张量的维度
t = tf.random.normal((2, 2))
print(t)
# 增加第一维度
t = tf.expand_dims(t, axis = 0)
print(t)
# 增加第四维度
t = tf.expand_dims(t, axis = 3)
print(t)
tf.Tensor(
[[-1.4346067 -0.69587547][-2.1144965 0.55389005]], shape=(2, 2), dtype=float32)
tf.Tensor(
[[[-1.4346067 -0.69587547][-2.1144965 0.55389005]]], shape=(1, 2, 2), dtype=float32)
tf.Tensor(
[[[[-1.4346067 ][-0.69587547]][[-2.1144965 ][ 0.55389005]]]], shape=(1, 2, 2, 1), dtype=float32)
从结果可以看出,增加了两个维度
使用tf.squeeze()可以减少张量的维度
import tensorflow as tft = tf.constant([[[[1], [2]]]])
print(t)
# 减少最后一个维度
t = tf.squeeze(t, axis = 3)
print(t)
tf.Tensor(
[[[[1][2]]]], shape=(1, 1, 2, 1), dtype=int32)
tf.Tensor([[[1 2]]], shape=(1, 1, 2), dtype=int32)
这里需要注意,减少的维度必须是1
(1, 2, 2, 2) 不能减少第四维度,即不能减少为(1, 2, 2, 2),但可以减少第一维度变成(2 ,2 ,2)
(8) 维度交换
使用tf.expand_dims()可以增加张量的维度
import tensorflow as tft = tf.zeros((1, 28, 28, 1))
print(t)
t = tf.transpose(t, [2, 3, 1, 0])
print(t)
[[[[ ... ]]]], shape=(1, 28, 28, 1), dtype=float32)
[[[[ ... ]]]], shape=(28, 1, 28, 1), dtype=float32)
每一个维度对应一个下标,从0开始
(1, 28, 28, 1) -> (0, 1, 2, 3)
tf.transpose()函数通过写下标的序号,把对应的维度进行交换
(2, 3, 1, 0) -> (28, 1, 28, 1)
4. 字符串张量
| 方法 | 作用 |
|---|---|
tf.strings.as_string(input, precision, scientific) | 转为字符串张量 |
tf.strings.bytes_split(input, name) | 分割每一个字符 |
tf.strings.split(input, sep) | 按照指定字符分割字符串 |
tf.strings.join(inputs, separator) | 字符串拼接 |
tf.strings.upper(input, encoding) | 将字符串转为大写 |
tf.strings.lower(input, encoding) | 将字符串转为小写 |
(1) 转为字符串张量
import tensorflow as tfstring = tf.constant([1.0, 2.0])
print(string)
t = tf.strings.as_string(string)
print(t)
t = tf.strings.as_string(string, precision = 3)
print(t)
tf.Tensor([1. 2.], shape=(2,), dtype=float32)
tf.Tensor([b'1.000000' b'2.000000'], shape=(2,), dtype=string)
tf.Tensor([b'1.000' b'2.000'], shape=(2,), dtype=string)
(2) 字符串分割
import tensorflow as tfstring = tf.constant('H e l l o')
print(tf.strings.bytes_split(string))
print(tf.strings.split(string, ' '))
tf.Tensor([b'H' b' ' b'e' b' ' b'l' b' ' b'l' b' ' b'o'], shape=(9,), dtype=string)
tf.Tensor([b'H' b'e' b'l' b'l' b'o'], shape=(5,), dtype=string)
(3) 字符串拼接
import tensorflow as tfstring = tf.constant([b'H' b' ' b'e' b' ' b'l' b' ' b'l' b' ' b'o'])
print(tf.strings.join(string))
tf.Tensor(b'H e l l o', shape=(), dtype=string)
(3) 字符串大小写转换
import tensorflow as tfstring = tf.constant('aaa')
upper = tf.strings.upper(string)
lower = tf.strings.lower(string)
print(upper)
print(lower)
tf.Tensor(b'AAA', shape=(), dtype=string)
tf.Tensor(b'aaa', shape=(), dtype=string)
5. 不规则张量
| 方法 | 作用 |
|---|---|
tf.ragged.constant(pylist, dtype) | 创建不规则张量 |
tf.ragged.map_flat_values(op, *args) | 对不规则张量进行数学变换 |
(1) 创建不规则张量
使用tf.ragged.constant()创建不规则张量
import tensorflow as tft = tf.ragged.constant([[1, 2], [], [1, 2, 3]])
print(t)
<tf.RaggedTensor [[1, 2], [], [1, 2, 3]]>
不规则张量类似Java中的数组,每一行的元素个数可以不一致
不规则张量中的所有元素类型必须是一致的
(2) 不规则张量的运算
import tensorflow as tft = tf.ragged.constant([[1, 2], [], [1, 2, 3]])
print(t + 2)
print(tf.subtract(t, 2))
print(t * 2)
print(tf.divide(t, 2))
<tf.RaggedTensor [[3, 4], [], [3, 4, 5]]>
<tf.RaggedTensor [[-1, 0], [], [-1, 0, 1]]>
<tf.RaggedTensor [[2, 4], [], [2, 4, 6]]>
<tf.RaggedTensor [[0.5, 1.0], [], [0.5, 1.0, 1.5]]>
同样的,不规则张量也支持普通张量的四则运算、乘法、开平方等
相同形状的不规则张量之间可以做四则运算、乘法、开平方等
import tensorflow as tfa = tf.ragged.constant([[1, 2], [], [1, 2, 3]])
b = tf.ragged.constant([[5, 6], [], [1, 2, 3]])
print(a + b)
print(tf.subtract(a, b))
print(a * b)
print(tf.divide(a, b))
<tf.RaggedTensor [[6, 8], [], [2, 4, 6]]>
<tf.RaggedTensor [[-4, -4], [], [0, 0, 0]]>
<tf.RaggedTensor [[5, 12], [], [1, 4, 9]]>
<tf.RaggedTensor [[0.2, 0.3333333333333333], [], [1.0, 1.0, 1.0]]>
如果形状不同,会报错
(3) 不规则张量的数学变换
使用tf.ragged.map_flat_values()对张量进行数学变换
import tensorflow as tfa = tf.ragged.constant([[1, 2], [], [1, 2, 3]])
print(a)
print(tf.ragged.map_flat_values(lambda x: x + 3, a))
<tf.RaggedTensor [[1, 2], [], [1, 2, 3]]>
<tf.RaggedTensor [[4, 5], [], [4, 5, 6]]>
相关文章:

学习Tensorflow之基本操作
学习Tensorflow之基本操作Tensorflow基本操作1. 创建张量(1) 创建标量(2) 创建向量(3) 创建矩阵(4) shape属性(5) 判别张量类型(6) 列表和ndarray转张量2. 创建特殊张量(1) tf.ones与tf.ones_like(2) tf.zeros与tf.zeros_like(3) tf.fill(3) tf.random.normal(4) tf.random.uni…...
《Spring系列》第2章 解析XML获取Bean
一、基础代码 Spring加载bean实例的代码 public static void main(String[] args) throws IOException {// 1.获取资源Resource resource new ClassPathResource("bean.xml");// 2.获取BeanFactoryDefaultListableBeanFactory factory new DefaultListableBeanFa…...

小红书20230326暑假实习笔试
第一题:加密 小明学会了一种加密方式。他定义suc(x)为x在字母表中的后继,例如a的后继为b,b的后继为c… (即按字母表的顺序后一个)。特别的,z的后继为a。对于一个原字符串S,将其中每个字母x都替…...
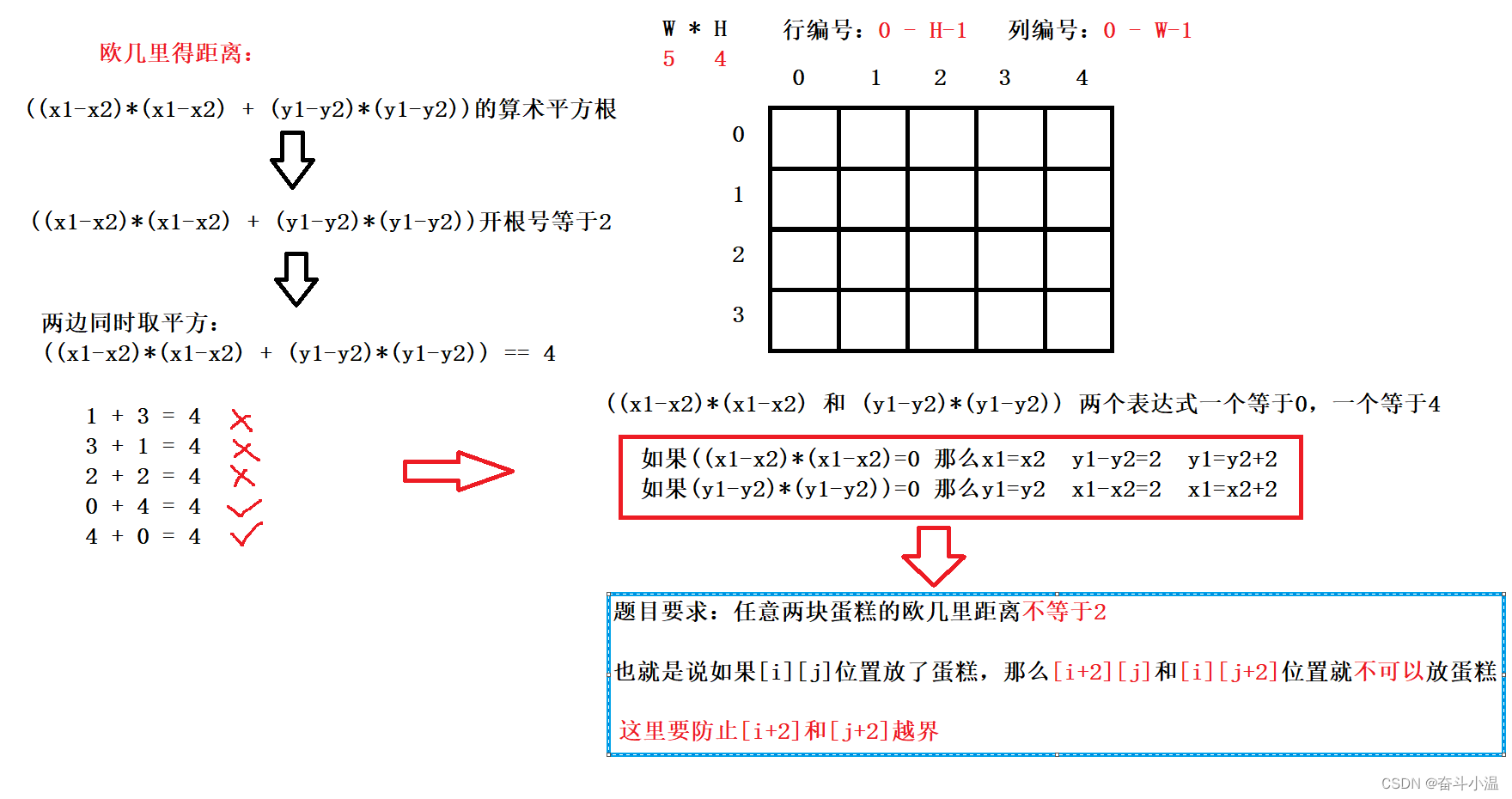
【java】不要二、把字符串转成整数
目录 🔥一、编程题 1.不要二 2.把字符串转换成整数 🔥一、编程题 1.不要二 链接:不要二_牛客题霸_牛客网 (nowcoder.com) 描述:二货小易有一个W*H的网格盒子,网格的行编号为0~H-1,网格的列编号为0~W-1…...

数据的质量管控工作
数据的质量管控工作,整个工作应该围绕启动阶段制定的目标进行。适当引入一些质量管控工具可帮助我们更高效的完成工作。 第一步、数据剖析 首先应该进行已知数据问题的评估,这里评估的范围也应控制本轮管控的目标范围内。其次,通过对数据进行…...

【SpringBoot笔记29】SpringBoot集成RabbitMQ消息队列
这篇文章,主要介绍SpringBoot如何集成RabbitMQ消息队列。 目录 一、集成RabbitMQ 1.1、引入amqp依赖 1.2、添加连接信息 1.3、添加RabbitMQ配置类...

前端架构师-week2-脚手架架构设计和框架搭建
将收获什么 脚手架的实现原理 Lerna的常见用法 架构设计技巧和架构图绘制方法 主要内容 学习如何以架构师的角度思考基础架构问题 多 Package 项目管理痛点和解决方案,基于 Lerna 脚手架框架搭建 imooc-cli 脚手架需求分析和架构设计,架构设计图 附赠内…...

CMake项目实战指令详细分析
CMake是一个跨平台的自动化构建系统,可以用简单的语句来描述所有平台的编译过程。CMake可以输出各种各样的编译文件,如Makefile、VisualStudio等。 CMake主要是编写CMakeLists.txt文件,然后用cmake命令将CMakeLists.txt文件转化为make所需要的…...

【深度学习】——LSTM参数设置
批大小设置 LSTM的批大小可以根据训练数据集的大小和计算资源的限制来确定。一般而言,批大小越大,训练速度越快,但可能会导致过拟合和内存限制。批大小越小,训练速度越慢,但对于较大的数据集和内存限制较严格的情况下…...
计算机网络高频60问 背完差不多了!!
计算机网络高频60问 网络分层结构 计算机网络体系大致分为三种,OSI七层模型、TCP/IP四层模型和五层模型。一般面试的时候考察比较多的是五层模型。 五层模型:应用层、传输层、网络层、数据链路层、物理层。 应用层:为应用程序提供交互服务…...
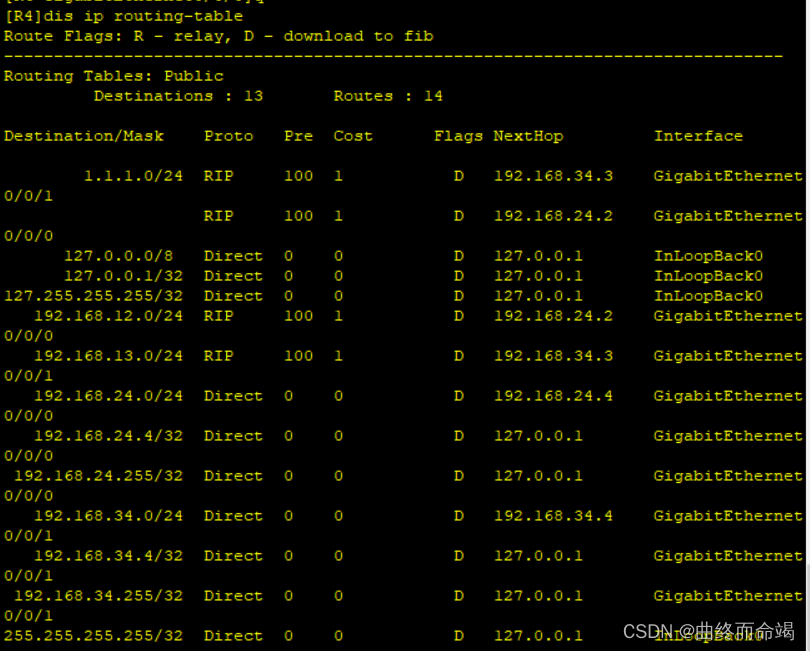
路由策略小实验
实验要求: 1、R1环回使用重发布,R2和R3使用双向重发布 2、使用路由策略解决,选路不佳 第一步,基础配置 [R1]int l0 [R1-LoopBack0]ip add 1.1.1.1 24 [R1-LoopBack0]int g0/0/0 [R1-GigabitEthernet0/0/0]ip add 192.168.12.1 …...

C语言realloc背后的内存管理
malloc申请内存,但不初始化。 calloc申请内存,且初始化为0。 free释放内存。 realloc重新分配已经分配的内存空间,可以变小,也可以变大。 以前一直有一个疑问,realloc是不是经常失败? 其实,rea…...

GPT可以被放任的在问答区应用吗?
GPT可以被放任的在问答区应用吗?1、CSDN问答乱象2、GPT-4,大增长时代的序幕数字生命离我们到底还有多远?AI 家教/老师/教育 距离独立又有哪些需要完成的过程?3、老顾对CSDN问答的一些看法老顾对GPT使用者的一些建议1、CSDN问答乱象…...
)
限制网络接口的一些简介(一)
大家在上网的时候,我们设置了www,当有来自internet的www要求时,我们的主机就会予以响应。这是因为你的主机已经开启了www的监听端口。所以,当我们启用一个daemon时,就可能触发主机的端口进行监听的动作,此时…...

ChatGPT如何批量撰写最新的热点自媒体文章
如何用ChatGPT创作高质量的自媒体文章 自媒体已成为互联网上的一个重要组成部分,无论您是想在社交媒体、博客中发布内容,高质量的文章都是自媒体成功的重要组成部分。ChatGPT是一个智能文章生成器,能够帮助创作者快速、高效地生成高质量的自…...
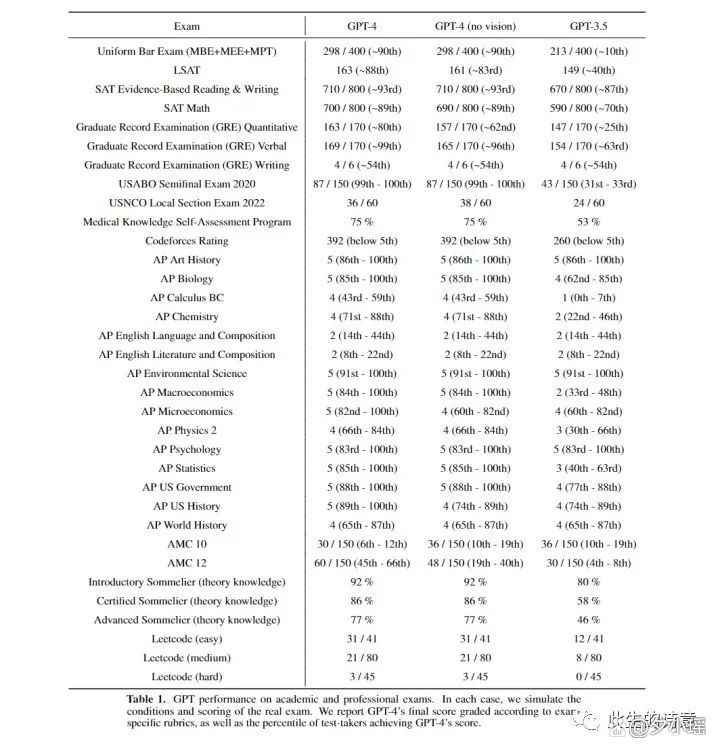
GPT4和ChatGPT的区别,太让人震撼
文 | Serendipity知乎 前言 GPT4上午朋友圈已经刷屏啦,不过我还在忙,刚刚才登上 GPT-4 ,现在来体验一下~ 附 GPT-4 能力测试站(无需魔法,仅供国内研究测试): https://gpt4test.com 附 Cha…...
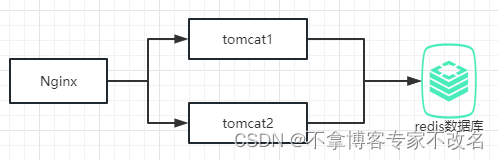
redis实战---分布式锁--单机篇
redis分布式锁故事背景什么是Redis分布式锁业务场景未加任何锁的代码单机情况下JVM级别加锁多服务部署总结提升故事背景 本篇文章是redis实战系列的第二篇文章。本章的主要内容是Redis分布式锁的相关知识。本篇文章将告诉你什么是分布式锁,结合一个业务场景&#x…...

Java正则表达式
Java 正则表达式 文章目录Java 正则表达式捕获组正则表达式语法Matcher 类的方法索引方法查找方法替换方法start 和 end 方法matches 和 lookingAt 方法replaceFirst 和 replaceAll 方法appendReplacement 和 appendTail 方法PatternSyntaxException 类的方法正则表达式是对字符…...
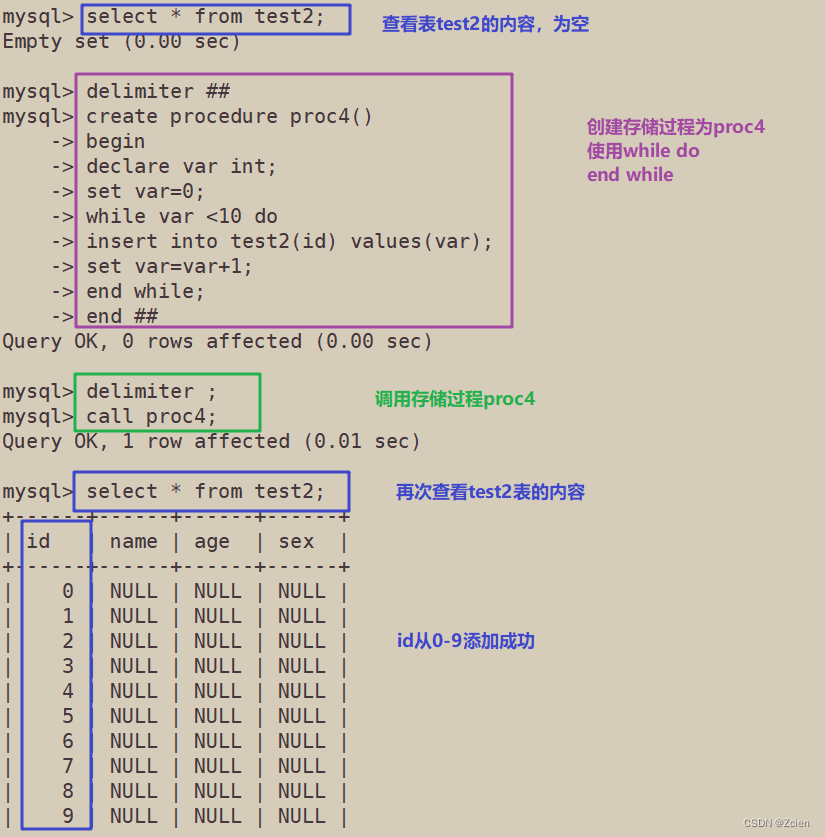
MySQL数据库之——高级[进阶]SQL语句(二)正则表达式和存储过程
文章目录一、正则表达式(REGEXP)1、正则表达式匹配符2、语法二、存储过程1、概述2、优点3、 创建、调用、查看和删除存储过程4、存储过程的控制语句一、正则表达式(REGEXP) 1、正则表达式匹配符 2、语法 SELECT 选项 FROM 表名 …...

Python基于周立功盒子的二次开发的准备工作
Python基于周立功盒子的二次开发的准备工作 一、基本介绍 基于周立功的二次开发是python通过调用zlgcan.dll,来实现CAN卡的通讯收发报文的,在python中通过ctypes模块调用c++动态库的接口函数(zlgcan.dll),我们需要根据我的电脑选择相对应版本的dll,比如64位的操…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
