【代码随想录训练营第42期 Day61打卡 - 图论Part11 - Floyd 算法与A * 算法

目录

一、Floyd算法与A * 算法

1、Floyd算法

思想

伪代码

2、 A * 算法

思想

伪代码

二、经典题目

题目一：卡码网 97. 小明逛公园

题目链接

题解：Floyd 算法

题目二：卡码网 127. 骑士的攻击

题目链接

 题解：A * 算法（A-Star）

三、小结

---

一、Floyd算法与A * 算法

1、Floyd算法

思想

Floyd算法的基本思想是逐步迭代地考虑图中的所有顶点，并更新任意两点之间的最短路径长度。在每一步迭代中，算法检查所有顶点对（i，j），并通过当前考虑的顶点k，看是否能够找到一条从i到j的更短路径。具有能够找到图中任意两点间的最短路径的优势，适合解决多源最短路，即求多个起点到多个终点的多条最短路径。

Floyd算法核心思想是动态规划。

伪代码

function floydWarshall(weights, V):let dist be a V x V arrayfor i from 0 to V-1:for j from 0 to V-1:if i == j:dist[i][j] = 0else if there is an edge from i to j:dist[i][j] = weight of the edge from i to jelse:dist[i][j] = INFINITYfor k from 0 to V-1:for i from 0 to V-1:for j from 0 to V-1:if dist[i][k] + dist[k][j] < dist[i][j]:dist[i][j] = dist[i][k] + dist[k][j]return dist

2、 A * 算法

入门建议观看视频：【A*寻路算法详解 #A星 #启发式搜索】

思想

A算法（A-Star算法）是一种在图形平面上，有多个节点的路径中，寻找一条从起点到终点的最短路径的算法。它的设计思想主要结合了实际代价和启发式估计，以高效地搜索图形中的最优路径。

核心思想是将启发式搜索和最佳优先搜索结合起来，以寻找从起始点到目标点的最短路径。

伪代码

function A*(start, goal)open_list = priority_queue() // 优先队列，按f值排序start.g = 0start.h = heuristic(start, goal)start.f = start.g + start.hstart.parent = nullopen_list.add(start)while not open_list.is_empty()current = open_list.pop() // 取出f值最小的节点if current == goalreturn reconstruct_path(current)closed_list.add(current) // 将当前节点加入封闭列表for neighbor in neighbors(current)if neighbor in closed_listcontinuetentative_g = current.g + distance(current, neighbor)if neighbor not in open_list or tentative_g < neighbor.gneighbor.parent = currentneighbor.g = tentative_gneighbor.h = heuristic(neighbor, goal)neighbor.f = neighbor.g + neighbor.hif neighbor not in open_listopen_list.add(neighbor)return null // 没有找到路径function reconstruct_path(node)path = []while node is not nullpath.prepend(node)node = node.parentreturn path.reverse() // 反转路径以从起点到终点function heuristic(node, goal)// 返回从node到goal的启发式估计值
end functionfunction neighbors(node)// 返回node的邻居节点列表
end functionfunction distance(node1, node2)// 返回从node1到node2的实际距离
end function

二、经典题目

题目一：卡码网 97. 小明逛公园

题目链接

97. 小明逛公园 (kamacoder.com)

题目描述

小明喜欢去公园散步，公园内布置了许多的景点，相互之间通过小路连接，小明希望在观看景点的同时，能够节省体力，走最短的路径。 

给定一个公园景点图，图中有 N 个景点（编号为 1 到 N），以及 M 条双向道路连接着这些景点。每条道路上行走的距离都是已知的。

小明有 Q 个观景计划，每个计划都有一个起点 start 和一个终点 end，表示他想从景点 start 前往景点 end。由于小明希望节省体力，他想知道每个观景计划中从起点到终点的最短路径长度。 请你帮助小明计算出每个观景计划的最短路径长度。

输入描述

第一行包含两个整数 N, M, 分别表示景点的数量和道路的数量。 

接下来的 M 行，每行包含三个整数 u, v, w，表示景点 u 和景点 v 之间有一条长度为 w 的双向道路。 

接下里的一行包含一个整数 Q，表示观景计划的数量。 

接下来的 Q 行，每行包含两个整数 start, end，表示一个观景计划的起点和终点。

输出描述

对于每个观景计划，输出一行表示从起点到终点的最短路径长度。如果两个景点之间不存在路径，则输出 -1。

输入示例

7 3
2 3 4
3 6 6
4 7 8
2
2 3
3 4

输出示例

4
-1

提示信息

从 2 到 3 的路径长度为 4，3 到 4 之间并没有道路。

1 <= N, M, Q <= 1000.

题解：Floyd 算法

关键在于Floyd算法的实现，即：

使用三重循环来实现Floyd算法：

外层循环变量 k 代表中间节点，内两层循环变量 i 和 j 分别代表起点和终点。

在每一轮循环中，检查通过中间节点 k 从 i 到 j 的路径是否比当前已知的路径更短，如果是，则更新 grid[i][j]。

代码实现：

 for (int k = 1; k <= n; k++) // k代表中间节点{for (int i = 1; i <= n; i++) // i代表起点{for (int j = 1; j <= n; j++) // j代表终点{grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j]); // 更新i到j的最短路径，如果通过k的路径更短，则更新}}}

完整代码如下：

#include <bits/stdc++.h>
using namespace std;int main()
{int n, m, p1, p2, val;cin >> n >> m;vector<vector<int>> grid(n + 1, vector<int>(n + 1, 10005)); // 创建一个二维向量grid来存储图的邻接矩阵，因为边的最大距离为10**4// 读取m条边的信息，并更新邻接矩阵for (int i = 0; i < m; i++){cin >> p1 >> p2 >> val;grid[p1][p2] = val;grid[p2][p1] = val; // 注意这里是双向图：需要考虑两个方向}// 开始 floyd 算法for (int k = 1; k <= n; k++) // k代表中间节点{for (int i = 1; i <= n; i++) // i代表起点{for (int j = 1; j <= n; j++) // j代表终点{grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j]); // 更新i到j的最短路径，如果通过k的路径更短，则更新}}}// 输出结果int Q, start, end;cin >> Q;while (Q--){cin >> start >> end;if (grid[start][end] == 10005) // 如果最短路径长度仍然是初始值，表示没有路径cout << -1 << endl;elsecout << grid[start][end] << endl;}return 0;
}

题目二：卡码网 127. 骑士的攻击

题目链接

127. 骑士的攻击 (kamacoder.com)

题目描述

在象棋中，马和象的移动规则分别是“马走日”和“象走田”。现给定骑士的起始坐标和目标坐标，要求根据骑士的移动规则，计算从起点到达目标点所需的最短步数。

棋盘大小 1000 x 1000（棋盘的 x 和 y 坐标均在 [1, 1000] 区间内，包含边界）

输入描述

第一行包含一个整数 n，表示测试用例的数量，1 <= n <= 100。

接下来的 n 行，每行包含四个整数 a1, a2, b1, b2，分别表示骑士的起始位置 (a1, a2) 和目标位置 (b1, b2)。

输出描述

输出共 n 行，每行输出一个整数，表示骑士从起点到目标点的最短路径长度。

输入示例

6
5 2 5 4
1 1 2 2
1 1 8 8
1 1 8 7
2 1 3 3
4 6 4 6

输出示例

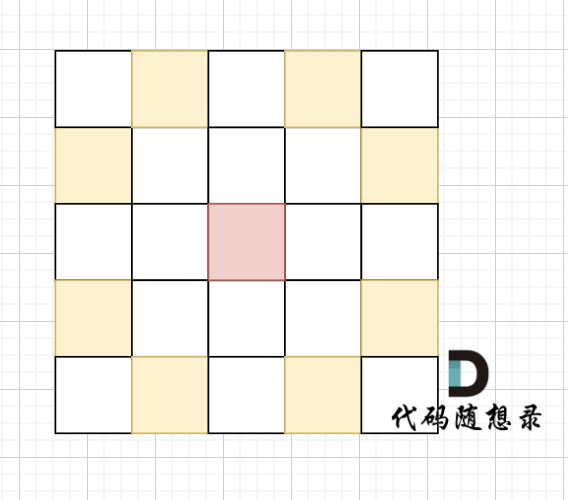
2
4
6
5
1
0

提示信息

骑士移动规则如图，红色是起始位置，黄色是骑士可以走的地方。

 题解：A * 算法（A-Star）

关键在于A*算法实现的部分：

在astar函数中，使用优先队列来存储当前的Knight对象；

循环直到优先队列为空，即所有可能的路径都被检查过；

在每次循环中，从优先队列中取出F值最小的Knight对象，并检查是否到达目标位置；

如果未到达目标位置，则遍历8个可能的方向，计算下一个位置的坐标，并检查是否越界或已经被访问过；

如果下一个位置合法且未被访问过，则更新路径消耗，计算F值，并将其加入优先队列；

当到达目标位置时，循环结束。

实现代码：

void astar(const Knight &k)
{Knight cur, next;que.push(k);while (!que.empty()){cur = que.top();que.pop();if (cur.x == b1 && cur.y == b2)break;for (int i = 0; i < 8; i++) // 遍历骑士的8个可能移动方向{// 得到下一个位置的坐标next.x = cur.x + dir[i][0];next.y = cur.y + dir[i][1];if (next.x < 1 || next.x > 1000 || next.y < 1 || next.y > 1000) // 如果下一个位置越界，则跳过continue;if (!moves[next.x][next.y]) // 如果下一个位置没有被访问过{moves[next.x][next.y] = moves[cur.x][cur.y] + 1; // 更新下一个位置的路径消耗// 开始计算Fnext.g = cur.g + 5;       // 统一不开根号，这样可以提高精度，马走日，1 * 1 + 2 * 2 = 5next.h = Heuristic(next); // 计算当前节点到终点的预估消耗next.f = next.g + next.h; // 计算F值que.push(next);           // 将下一个位置的Knight对象加入优先队列}}}
}

 完整代码实现：

#include <bits/stdc++.h>
using namespace std;int moves[1001][1001];                                              // 定义一个二维数组moves，用于存储骑士从起点到当前位置的移动步数
int dir[8][2] = {-2, -1, -2, 1, -1, 2, 1, 2, 2, 1, 2, -1, 1, -2, -1, -2}; // 定义一个方向数组dir，用于存储骑士可能的移动方向
int b1, b2;struct Knight // 定义一个结构体Knight，用于存储骑士的当前位置和路径消耗等信息
{int x, y;int g, h, f;bool operator<(const Knight &k) const // 重载运算符，用于优先队列的排序{return k.f < f; // 从小到大排序}
};priority_queue<Knight> que; // 定义一个优先队列que，用于存储Knight对象，并按照f值排序int Heuristic(const Knight &k) // 欧拉距离
{return (k.x - b1) * (k.x - b1) + (k.y - b2) * (k.y - b2); // 统一不开根号，这样可以提高精度
}
// 执行A*算法：参数k是当前的Knight对象
void astar(const Knight &k)
{Knight cur, next;que.push(k);while (!que.empty()){cur = que.top();que.pop();if (cur.x == b1 && cur.y == b2)break;for (int i = 0; i < 8; i++) // 遍历骑士的8个可能移动方向{// 得到下一个位置的坐标next.x = cur.x + dir[i][0];next.y = cur.y + dir[i][1];if (next.x < 1 || next.x > 1000 || next.y < 1 || next.y > 1000) // 如果下一个位置越界，则跳过continue;if (!moves[next.x][next.y]) // 如果下一个位置没有被访问过{moves[next.x][next.y] = moves[cur.x][cur.y] + 1; // 更新下一个位置的路径消耗// 开始计算Fnext.g = cur.g + 5;       // 统一不开根号，这样可以提高精度，马走日，1 * 1 + 2 * 2 = 5next.h = Heuristic(next); // 计算当前节点到终点的预估消耗next.f = next.g + next.h; // 计算F值que.push(next);           // 将下一个位置的Knight对象加入优先队列}}}
}int main()
{int n, a1, a2;cin >> n;while (n--){cin >> a1 >> a2 >> b1 >> b2;memset(moves, 0, sizeof(moves)); // 每次循环都初始化moves数组为0，确保每个骑士问题都有独立的路径记录// 定义起点Knight对象start// F = G + H// G = 从起点到该节点路径消耗// H = 该节点到终点的预估消耗Knight start;start.x = a1;start.y = a2;start.g = 0;start.h = Heuristic(start);start.f = start.g + start.h;// 执行A*算法，以起点Knight对象start为起点astar(start);// 执行A*算法后，清空优先队列que，以便下一次循环使用while (!que.empty())que.pop();cout << moves[b1][b2] << endl; // 输出本次从起点到目标点的路径消耗，即moves[b1][b2]}return 0;
}

三、小结

这算是图论最后的内容了，难度很大，个人感觉只是理解了大概意思，却难以代码实现，后边二刷的时候会强化理解，继续加油！