计算1 / 1 - 1 / 2 + 1 / 3 - 1 / 4 + 1 / 5 …… + 1 / 99 - 1 / 100 的值,打印出结果
我们写这道题的时候需要俩变量接受,一个总数一个分母,我们发现分母变化是有规律的从1~100循环。
#include<stdio.h>
int main()
{int i = 0;int tag = 1;double sum = 0.0;for (i = 1; i < 101; i++){if (i % 2 == 0){sum = sum - 1.0 / i;}else{sum = sum + 1.0 / i;}}printf("%lf\n", sum);return 0;
}打印出结果的时候就有可能是有小数,所以需要double定义sum。
除此之外我们还发现有正负号的区分,但是有规律,我们就发现偶数是负数所以我们就区别开来

相关文章:

计算1 / 1 - 1 / 2 + 1 / 3 - 1 / 4 + 1 / 5 …… + 1 / 99 - 1 / 100 的值,打印出结果
我们写这道题的时候需要俩变量接受,一个总数一个分母,我们发现分母变化是有规律的从1~100循环。 #include<stdio.h> int main() {int i 0;int tag 1;double sum 0.0;for (i 1; i < 101; i){if (i % 2 0){sum sum - 1.0 / i;}else{sum s…...
Linux本地服务器搭建开源监控服务Uptime Kuma与远程监控实战教程
文章目录 前言**主要功能**一、前期准备本教程环境为:Centos7,可以跑Docker的系统都可以使用本教程安装。本教程使用Docker部署服务,如何安装Docker详见: 二、Docker部署Uptime Kuma三、实现公网查看网站监控四、使用固定公网地址…...

JS 历史简介
目录 1. JS 历史简介 2. JS 技术特征 1. JS 历史简介 举例:在提交用户的注册信息的时候,为避免注册出现错误后重新填写信息,可以在写完一栏信息后进行校验,并提示是否出现错误,这样会大大提高用户提交的成功率&…...

爬虫逆向学习(七):补环境动态生成某数四代后缀MmEwMD
声明:本篇文章内容是整理并分享在学习网上各位大佬的优秀知识后的实战与踩坑记录 前言 这篇文章主要是研究如何动态生成后缀参数MmEwMD的,它是在文章爬虫逆向学习(六):补环境过某数四代的基础上进行研究的,代码也是在它基础上增…...

光伏电站并网验收需要注意什么细节
一、设备质量及安装验收 光伏组件:检查光伏组件的外观是否完好无损,无明显的缺陷和破损,表面是否清洁无污染。同时,需要验证光伏组件的型号、参数是否与设备台账资料一致。 逆变器:确认逆变器具备防雷、防尘、防潮等…...

页面禁用鼠标右键属于反爬虫措施吗 ?
是的,禁用鼠标右键通常被视为一种反爬虫(anti-scraping)措施。网站开发者常常采用这种技术来防止用户通过右键菜单复制文本、图像或其他内容,特别是在内容保护和数据安全方面。以下是禁用鼠标右键的一些背景和目的: 1…...
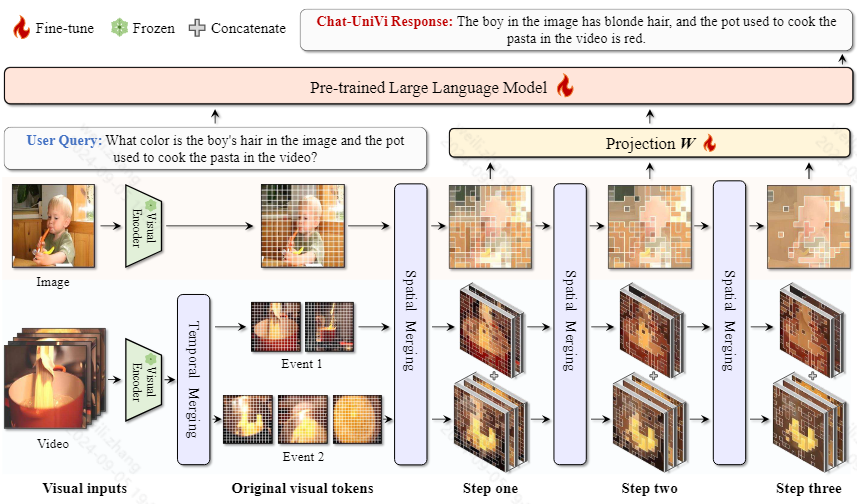
视频理解大模型最新进展
文章目录 Video-LLaMAVision-Language BranchAudio-Language Branch Video-ChatGPTMiniGPT4-videoCogVLM2-Video(1)Pre-training(2)Post-training Qwen2-VLMA-LMMChat-UniVi大模型对比 Video-LLaMA 2023:阿里达摩院的…...

cocos creator 使用 protobuf 的步骤与注意事项
移除可能曾安装过的protobuf // 移除全局 npm remove -g protobufjs npm remove -g protobufjs-cli npm remove -g pbjs // 移除项目中的 npm remove --save protobufjs npm remove --save protobufjs-cli npm remove --save pbjs全局安装 npm i -g protobufjs //或者 cnpm …...

mac访达查找文件目录
mac访达查找文件目录 在Mac上使用访达(Finder)查找文件或目录的方法如下: 打开访达。 在访达窗口的侧边栏中,选择“ Go to Folder”(转到文件夹)选项,或者使用快捷键ShiftCommandG打开一个对…...

【数据结构】点分治 点分树
求树上长度小于等于k的路径 #include <iostream> #include <cstring> #include <algorithm>using namespace std;const int N 10010, M N * 2;int n, m; int h[N], e[M], w[M], ne[M], idx; //邻接表 bool st[N]; //记录每个点是否被删掉 int p[N]; //存储…...

K8s Calico替换为Cilium,以及安装Cilium过程(鲁莽版)
迁移CNI插件的3种办法: 1、创建一个新的集群,通过Gitops的方式迁移负载,然而,这可能涉及大量的准备工作和潜在的中断。 2、另一种方法是重新配置/etc/cni/net.d/指向Cilium。但是,现有的pod仍将由旧的…...

背景图鼠标放上去切换图片过渡效果
文章目录 css鼠标放上去之前效果鼠标放上去时效果 css <li class"message"></li>.message {width: 22px;height: 22px;background-image: url(/assets/message-01.png);background-size: cover;background-position: center;transition: background-ima…...

【Linux】当前进展
驱动层日志添加了下文件目录,函数,代码行的打印(这里要小心,驱动目录源代码打印日志里边添进程号可能有问题,因为在驱动初始化的时候,内核还没有创建进程,不过猜测可以先不打印进程相关信息&…...

阿里云云效多个ssh密钥对配置
实现功能 windows本地多个ssh密钥对,分别对应不同的阿里云账号的云效 实现办法 1.生成ssh密钥对 ssh-keygen -t rsa -f C:\xxx\id_rsa_customname(我这里C:\Users\admin\.ssh\id_rsa_customname) 2.配置.ssh目录的config文件 # ruiyi Host customnameHostName codeup.al…...

前后端跨域问题及其在ThinkPHP中的解决方案
在现代Web开发中,前后端分离的架构越来越普遍,但这也带来了跨域问题。跨域指的是在一个域下的网页试图请求另一个域的资源,浏览器出于安全考虑会限制这种行为。本文将探讨如何在ThinkPHP中解决跨域问题。 #### 1. 什么是跨域? 跨…...
)
基于CentOS7上安装MicroK8s(最小生产的 Kubernetes)
简介 MicroK8s是一个轻量级的Kubernetes发行版,其内存和存储要求远低于全尺寸Kubernetes集群。它可以在几分钟内通过一条命令快速创建功能齐全的Kubernetes集群,极大地简化了部署过程。 兼容性:MicroK8s与Kubernetes全面兼容,确保用户可以无缝迁移和扩展他们的应用程序。 …...

从《GTA5》的反外挂斗争看网络安全的重要性
摘要: 在网络游戏的世界里,外挂(作弊软件)一直是破坏游戏公平性和玩家体验的一大难题。作为一款深受全球玩家喜爱的游戏,《GTA5》(Grand Theft Auto V)在线模式也不例外地遭遇了外挂问题。本文将…...

python如何将字符转换为数字
python中的字符数字之间的转换函数 int(x [,base ]) 将x转换为一个整数 long(x [,base ]) 将x转换为一个长整数 float(x ) 将x转换到一个浮点数 complex(real [,imag ]) 创建一个复数 str(x ) 将对象 x 转换为字…...

TikTok流量不佳:是网络环境选择不当还是其他原因?
TikTok,作为全球短视频社交平台的佼佼者,每天都有海量的内容被上传和分享。然而,很多用户和内容创作者发现,他们的TikTok视频流量并不理想。这引发了一个问题:TikTok流量不佳,是因为网络环境选择不当&#…...

QT菜单栏设计(二级菜单栏)
目的:创建一级菜单栏,添加对应选项,并向一级菜单栏中添加二级菜单栏选项。 #include "mainwindow.h" #include "ui_mainwindow.h"MainWindow::MainWindow(QWidget *parent): QMainWindow(parent), ui(new Ui::MainWindo…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...
