深度学习:(八)深层神经网络参数与流程
深层神经网络
符号规定
- L L L :表示神经网络的层数;
- l l l :表示第几层;
- n [ l ] n^{[~l~]} n[ l ] :表示第 l l l 层的节点数;
- a [ l ] a^{[~l~]} a[ l ] :表示第 l l l 层中的激活函数(泛指);
- a [ l ] = g [ l ] ( z [ l ] ) a^{[~l~]}=g^{[~l~]}(z^{[~l~]}) a[ l ]=g[ l ](z[ l ]) :表示第 l l l 层中的激活函数(泛指);
- W [ l ] W^{[~l~]} W[ l ] :表示第 l l l 层的参数 w w w 的集合;
- b [ l ] b^{[~l~]} b[ l ] :表示第 l l l 层的参数 b b b 的集合。
前向传播和反向传播都类似之前的笔记。
流程图

前向传播有输入数据 x x x ,反向传播的输入数据是 d a [ L ] da^{[~L~]} da[ L ] ,即输出层(第 L L L 层)的输出,在向量化代码中,直接展示出来的结果是损失函数 L ( y ^ , y ) L(\widehat{y},y) L(y ,y) ,
因为 d a [ L ] = − y a + 1 − y 1 − a da^{[~L~]}=-\frac{y}{a}+\frac{1-y}{1-a} da[ L ]=−ay+1−a1−y ,而 L ( y ^ , y ) L(\widehat{y},y) L(y ,y) 对 y ^ \widehat{y} y ( a a a)的导数,正好等于这个结果。因此将损失函数对 y ^ \widehat{y} y ( a a a)求导,可得出 d a [ L ] da^{[~L~]} da[ L ] ,然后代入反向传播链的输入,开始迭代,如上图所示。
向量化时 d a [ L ] da^{[~L~]} da[ L ] 需改为 d A [ L ] dA^{[~L~]} dA[ L ] , d A [ L ] = ( d a [ 1 ] , d a [ 2 ] , . . . , d a [ m ] ) dA^{[~L~]}=(da^{[~1~]},da^{[~2~]},...,da^{[~m~]}) dA[ L ]=(da[ 1 ],da[ 2 ],...,da[ m ]) 。
为何 z [ l ] z^{[~l~]} z[ l ]是反向传播的一个输入参数
∵ a [ l ] = σ ( z [ l ] ) = σ ( W [ l ] a [ l − 1 ] + b [ l ] ) ∵ d L d a [ l − 1 ] = d L d a [ l ] ⋅ d a [ l ] d a [ l − 1 ] = d a [ l ] ⋅ σ ′ ( W [ l ] a [ l − 1 ] + b [ l ] ) W [ l ] ⋅ d a [ l − 1 ] ∴ d a [ l − 1 ] = d a [ l ] ⋅ σ ′ ( z [ l ] ) W [ l ] ⋅ d a [ l − 1 ] \begin{align*} ∵a^{[~l~]}=\sigma&(z^{[~l~]})=\sigma(W^{[~l~]}a^{[~l-1~]}+b^{[~l~]})\\ ∵\frac{dL}{da^{[~l-1~]}}&=\frac{dL}{da^{[~l~]}}·\frac{da^{[~l~]}}{da^{[~l-1~]}}\\ &=da^{[~l~]}·\sigma^{'}(W^{[~l~]}a^{[~l-1~]}+b^{[~l~]})W^{[~l~]}·da^{[~l-1~]}\\ ∴da^{[~l-1~]}&=da^{[~l~]}·\sigma^{'}(z^{[~l~]})W^{[~l~]}·da^{[~l-1~]} \end{align*} ∵a[ l ]=σ∵da[ l−1 ]dL∴da[ l−1 ](z[ l ])=σ(W[ l ]a[ l−1 ]+b[ l ])=da[ l ]dL⋅da[ l−1 ]da[ l ]=da[ l ]⋅σ′(W[ l ]a[ l−1 ]+b[ l ])W[ l ]⋅da[ l−1 ]=da[ l ]⋅σ′(z[ l ])W[ l ]⋅da[ l−1 ]
核对矩阵的维度
向量化前的单个样本
-
前向传播:
W [ l ] W^{[~l~]} W[ l ] :维度为 ( n [ l ] , n [ l − 1 ] ) (n^{[~l~]},n^{[~l-1~]}) (n[ l ],n[ l−1 ]) ;
z [ l ] z^{[~l~]} z[ l ] :维度为 ( n [ l ] , 1 ) (n^{[~l~]},1) (n[ l ],1) ;
a [ l ] a^{[~l~]} a[ l ] :维度为 ( n [ l ] , 1 ) (n^{[~l~]},1) (n[ l ],1) ;
b [ l ] b^{[~l~]} b[ l ] :维度为 ( n [ l ] , 1 ) (n^{[~l~]},1) (n[ l ],1) 。
-
反向传播:
d W [ l ] dW^{[~l~]} dW[ l ] 和 W [ l ] W^{[~l~]} W[ l ] 同维度;
d b [ l ] db^{[~l~]} db[ l ] 和 b [ l ] b^{[~l~]} b[ l ] 同维度。
向量化后的整个训练集
-
前向传播:
X ( A [ 0 ] ) X(A^{[~0~]}) X(A[ 0 ]) :维度为 ( n [ 0 ] , m ) (n^{[~0~]},m) (n[ 0 ],m) ;
W [ l ] W^{[~l~]} W[ l ] :维度为 ( n [ l ] , n [ l − 1 ] ) (n^{[~l~]},n^{[~l-1~]}) (n[ l ],n[ l−1 ]) ;
b [ l ] b^{[~l~]} b[ l ] :维度为 ( n [ l ] , 1 ) (n^{[~l~]},1) (n[ l ],1) ;# 要广播
Z [ l ] Z^{[~l~]} Z[ l ] :维度为 ( n [ l ] , m ) (n^{[~l~]},m) (n[ l ],m) ;
A [ l ] A^{[~l~]} A[ l ] :维度为 ( n [ l ] , m ) (n^{[~l~]},m) (n[ l ],m) 。
-
反向传播:
d W [ l ] dW^{[~l~]} dW[ l ] 和 W [ l ] W^{[~l~]} W[ l ] 同维度;
d b [ l ] db^{[~l~]} db[ l ] 和 b [ l ] b^{[~l~]} b[ l ] 同维度;
d Z [ l ] dZ^{[~l~]} dZ[ l ] 和 Z [ l ] Z^{[~l~]} Z[ l ] 同维度;
d A [ l ] dA^{[~l~]} dA[ l ] 和 A [ l ] A^{[~l~]} A[ l ] 同维度。
超参数:
能控制参数 w w w 和 b b b 的参数,需人为设置。
- 学习率 α \alpha α ;
- 梯度下降法循环次数;
- 隐层数 L L L ;
- 隐藏层的单元(节点)数;
- 激活函数类型。
这些参数需要不断测试,实时评估损失函数(横坐标越大,纵坐标越小)。
相关文章:

深度学习:(八)深层神经网络参数与流程
深层神经网络 符号规定 L L L :表示神经网络的层数; l l l :表示第几层; n [ l ] n^{[~l~]} n[ l ] :表示第 l l l 层的节点数; a [ l ] a^{[~l~]} a[ l ] :表示第 l l l 层中的激活函数&…...
(CNY|JPY|HKD|EUR|GBP|fen|cents|sen|eurocents|pence)“)
`pattern = r“(\d+)(CNY|JPY|HKD|EUR|GBP|fen|cents|sen|eurocents|pence)“
pattern r"(\d)(CNY|JPY|HKD|EUR|GBP|fen|cents|sen|eurocents|pence)" 是一个正则表达式,用于匹配特定格式的字符串。 正则表达式解析 整体结构: r"...":前缀 r 表示这是一个原始字符串(Raw String&#x…...
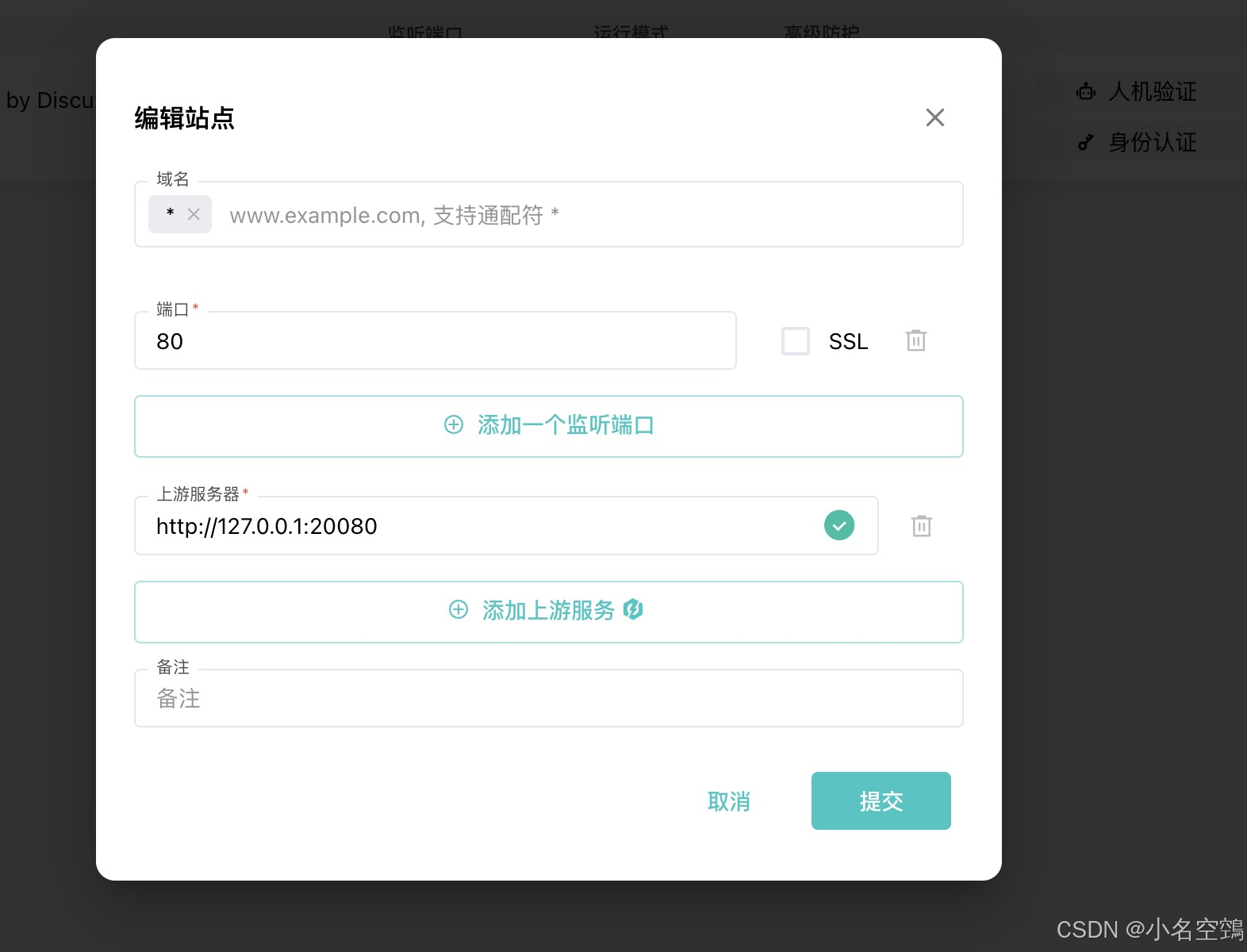
宝塔面板部署雷池社区版教程
宝塔面板部署雷池社区版教程 简单介绍一下宝塔面板,安全高效的服务器运维面板,使用宝塔面板的人非常多 在网站管理上,许多用户都是通过宝塔面板进行管理,宝塔面板的Nginx默认监听端口为80和443,这就导致共存部署时雷池…...

【击败100%】258. 各位相加
首次出现,代码用时击败了100%的用户,开心~ 题目 给定一个非负整数 num,反复将各个位上的数字相加,直到结果为一位数。返回这个结果。 示例 1: 输入: num 38 输出: 2 解释: 各位相加的过程为: 38 --> 3 8 -->…...

【alist】宝塔面板docker里的alist默认admin无法登录
宝塔docker安装完alist,根据页面的提示账号密码死活登录不上,提示密码有问题 页面提示: 数据存储目录 /www/dk_project/dk_app/dk_alist 使用说明请参考: >使用教程 默认账号密码(admin/admin) 首次登录后点击个人…...

【击败100%】1281. 整数的各位积和之差
击败了100%的用户,开心~ 题目 给你一个整数 n,请你帮忙计算并返回该整数「各位数字之积」与「各位数字之和」的差。 示例 1: 输入:n 234 输出:15 解释: 各位数之积 2 * 3 * 4 24 各位数之和 2 3 4 …...

Flink基本概念和算子使用
基础概念 Flink是一个框架和分布式处理引擎,用于对无界数据流和有界数据流进行有状态计算,它的核心目标是“数据流上的有状态计算”。 有界流和无界流 有界流:具有明确的开始和结束时间,数据量有限。适合使用批处理技术…...

Kafka 3.0.0集群部署教程
1、集群规划 主机名 ip地址 node.id process.roles kafka1 192.168.0.29 1 broker,controller Kafka2 192.168.0.30 2 broker,controller Kafka3 192.168.0.31 3 broker,controller 2、将kafka包上传以上节点/app目录下 mkdir /app 3、解压kafka包 所有节点 …...

昇思MindSpore进阶教程-格式转换
大家好,我是刘明,明志科技创始人,华为昇思MindSpore布道师。 技术上主攻前端开发、鸿蒙开发和AI算法研究。 努力为大家带来持续的技术分享,如果你也喜欢我的文章,就点个关注吧 MindSpore中可以把用于训练网络模型的数据…...

搜索软件 Everything 的安装与使用教程
一、Everything简介 适用于 Windows 的免费搜索工具 Everything 是 Windows 的即时搜索引擎。发现、整理并轻松访问文件和文件夹,一切尽在指尖! PS:Everything无法对文件内容进行搜索,只能根据文件名和路径进行搜索 二、Everyt…...

oracle 如何判断当前时间在27号到当月月底
在Oracle中,您可以使用TRUNC和LAST_DAY函数来判断当前时间是否在27号到当月月底之间。以下是一个SQL示例: SELECT CASE WHEN TRUNC(SYSDATE) > TRUNC(SYSDATE, DD) 26 AND TRUNC(SYSDATE) < LAST_DAY(SYSDATE) THEN 当前时间在27号到当月月底之间…...

Django 配置邮箱服务,实现发送信息到指定邮箱
一、这里以qq邮箱为例,打开qq邮箱的SMTP服务 二、django项目目录设置setting.py 文件 setting.py 添加如下内容: # 发送邮件相关配置 EMAIL_BACKEND django.core.mail.backends.smtp.EmailBackend EMAIL_USE_TLS True EMAIL_HOST smtp.qq.com EMAIL…...
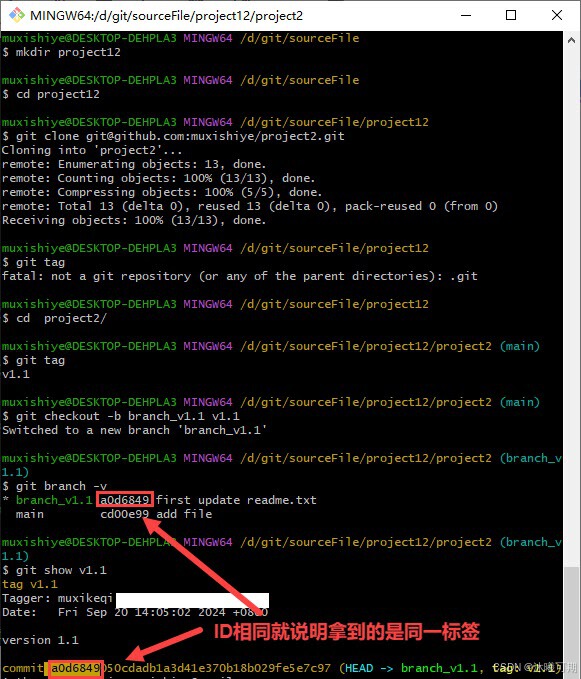
Git使用手册
1、初识Git 概述:Git 是一个开源的分布式版本控制系统,可以有效、高速地处理项目版本管理。 知识点补充: 版本控制:一种记录一个或若干文件内容变化,以便将来查阅特定版本修订情况的系统。 分布式:每个人…...

sql-labs靶场
第一关(get传参,单引号闭合,有回显,无过滤) ?id-1 union select 1,2,(select group_concat(table_name) from information_schema.tables where table_schemasecurity) -- 第二关(get传参,无闭…...

【Redis入门到精通二】Redis核心数据类型(String,Hash)详解
目录 Redis数据类型 1.String类型 (1)常见命令 (2)内部编码 2.Hash类型 (1)常见命令 (2)内部编码 Redis数据类型 查阅Redis官方文档可知,Redis提供给用户的核心数据…...

如何快速免费搭建自己的Docker私有镜像源来解决Docker无法拉取镜像的问题(搭建私有镜像源解决群晖Docker获取注册表失败的问题)
文章目录 📖 介绍 📖🏡 演示环境 🏡📒 Docker无法拉取镜像 📒📒 解决方案 📒🔖 方法一:免费快速搭建自己的Docker镜像源🎈 部署🎈 使用🔖 备用方案⚓️ 相关链接 🚓️📖 介绍 📖 在当前的网络环境下,Docker镜像的拉取问题屡见不鲜(各类Nas查询…...
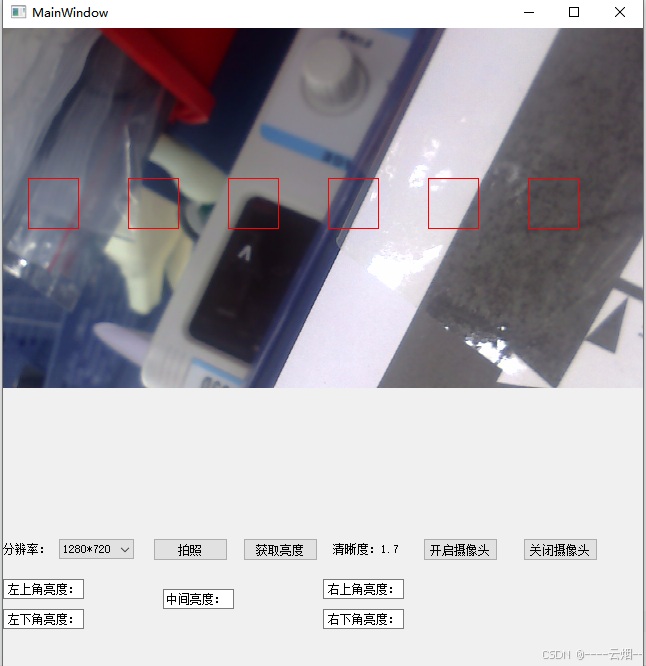
QT 获取视频帧Opencv获取清晰度
先展示结果: 1.获取摄像头的分辨率 mResSize.clear();mResSize camera_->supportedViewfinderResolutions();ui->comboBox_resulation->clear();int i0;foreach (QSize msize, mResSize) {qDebug()<<msize;ui->comboBox_resulation->addItem(…...

生成式AI如何辅助医药行业智能营销
生成式AI在医药行业的智能营销中发挥着日益重要的作用,它通过多种方式辅助医药企业提升市场洞察能力、优化营销策略、增强客户互动和体验,从而推动销售增长和品牌价值的提升。以下是生成式AI如何辅助医药行业智能营销的具体方式:一、精准市场…...
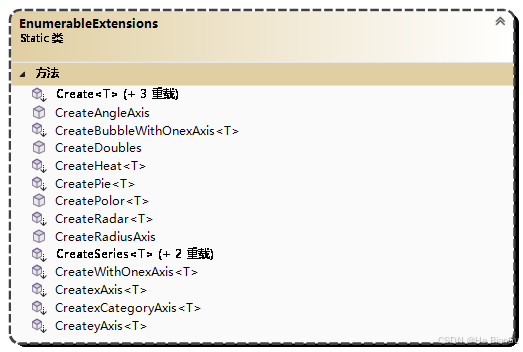
演示:基于WPF的DrawingVisual开发的Chart图表和表格绘制
一、目的:基于WPF的DrawingVisual开发的Chart图表和表格绘制 二、预览 钻井井轨迹表格数据演示示例(应用Table布局,模拟井轨迹深度的绘制) 饼图表格数据演示示例(应用Table布局,模拟多个饼状图组合显示&am…...

汽车保养BBBBBBBBBBB
小保养就是机油和机滤,4s店比较贵,可以在京东上买机油,可以包安装 极护、磁护 两款机油配方不同,极护系列机油注入液钛配方,拥有特别的油膜自适应能力,在各种形式条件下均能有效减少金属间的直接接触&…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
