matlab入门学习(四)多项式、符号函数、数据统计
一、多项式
%多项式(polynomial)%创建
p=[1,2,3,4] %系数向量,按x降幂排列,最右边是常数(x的0次幂)
f1=poly2str(p,'x') %系数向量->好看的字符串 f=' x^3 + 2 x^2 + 3 x + 4'(不能运算的式子,仅供查看)
f2=poly2sym(p) %系数向量->可用的符号函数 f=x^3 + 2*x^2 + 3*x + 4默认用x%求值
x=4;
y1=polyval(p,x) %polyval(系数向量,x)%求根
r=roots(p) %由系数求根
p0=poly(r) %由根求系数%数据插值%一维插值 yi=interp1(X,Y,xi,'method')
X=[-3,-1,0,1,3];
Y=[9,1,0,1,9];
yi=interp1(X,Y,2) %插值:估算在x=2的y的值(x不能查出已知范围)
yi=interp1(X,Y,2,'spline') %选择spline(三次样条法)进行插值,更精准但耗时长%二维插值 zi=interp1(X,Y,Z,xi,yi,'method')二、符号函数
创建符号函数、函数计算、精度转换;多项式的展开整理,求反函数
%符号函数syms x; %声明符号变量
f1=poly2sym([7,5])
f2=7*x+5 %创建符号函数(直接写出来即可)%符号函数计算
f=(3*x+2)*(4*x-1)
subs(f,x,4)
%subs 可以在符号表达式中将符号变量替换为其他值或表达式
% 例如:你有一个符号表达式 f 和一个符号变量 x,可以使用 subs(f, x, 4) 将 x 替换为 4%精度转换
digits %显示当前计算精度
digits(16) %修改精度
ans16=vpa(sqrt(2)) %按指定精度计算
ans8=vpa(sqrt(2),8) %修改精度,并按指定精度计算f=(3*x+2)*(4*x-1)
%多项式的展开整理
g=expand(f) %展开
h=collect(g) %整理,默认按x整理
h1=collect(g,x) %按x整理(降幂排列)%求反函数
fin=finverse(f,x) %对f中的x变量求反函数
求极限,泰勒展开;求微分,求积分
%极限
limit(f2,x,4) %求f(x),x->4
limit(f2,4) %默认变量->4
limit(f2) %默认变量->0
limit(f2,x,4,'right') %求右极限,x->4+ 'left'求左极限%泰勒展开
f3=sin(x)
taylor(f3,x,4) %将f3在x=4处展开成五阶泰勒级数(默认变量,默认在0处)%微分(求偏导)
diff(f,x,2) %f1对x的2阶导,相当于diff(f,x,x)
diff(f) %(默认变量,默认一阶导)
%多元偏导
fxy=diff(f,x,y) %先对x求偏导,再对y求偏导
fxyz=diff(f,x,y,z)%积分
int(f,x,1,2) %f对x在1-2上积分(不写x则认为是默认变量,不写区间则认为是不定积分)
int(f)方程求解(线性、非线性)
syms x y; % 正确声明符号变量a = 4; b = 10;% 线性一元方程
eqn1 = a*x == b; % 生成符号方程式
Sx = solve(eqn1); % solve求解% 线性多元方程组
e1 = x + y == a; %生成符号方程式
e2 = x - y == b;
[Sx, Sy] = solve(e1, e2, x, y); % 求解方程组(方程1,方程2,...,变量1,变量2,...)按顺序写变量,与Sx,Sy呼应%非线性
f=@(var) [var(1)^2+var(2)^2-100; var(1)-var(2)-2];
initGuess=[6,6];
S=fsolve(f,initGuess) %fsolve(@函数名称/ 函数句柄,求解的起始点,option),至少包含两个参数
%注意:handle = @myFunction; 将函数名称转换为函数句柄
三、数据统计
%数据统计A=[1,2,3;4,5,6;7,8,9]%最大值
A_m=max(A)
[A_m,k]=max(A) %没写则默认维度是1,求每列的最大值,k接收下标
[A_m,k]=max(A,[],2) %求每行的最大值%均值
mean(A) %每一列
mean(A,2) %每一行%中值
median(A) %每一列
median(A,2) %每一行sum(A); sum(A,2);
prod(A); prod(A,2); %求积
cumsum(A); cumsum(A,2) %累加->对每一行,逐元素累加(仍是m*n矩阵)
cumprod(A); cumprod(A,2) %累乘%排序
Y=sort(A,1,"ascend") %对矩阵的列向量进行升序排序(ascend)降序(descend)
[Y,I]=sort(A,1,'descend') %I保存了列元素之前的位置相关文章:
多项式、符号函数、数据统计)
matlab入门学习(四)多项式、符号函数、数据统计
一、多项式 %多项式(polynomial)%创建 p[1,2,3,4] %系数向量,按x降幂排列,最右边是常数(x的0次幂) f1poly2str(p,x) %系数向量->好看的字符串 f x^3 2 x^2 3 x 4(不能运算的式子…...

leetcode621. 任务调度器
给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表,用字母 A 到 Z 表示,以及一个冷却时间 n。每个周期或时间间隔允许完成一项任务。任务可以按任何顺序完成,但有一个限制:两个 相同种类 的任务之间必须有长度为 n 的冷却时…...

Spark 的 Skew Join 详解
Skew Join 是 Spark 中为了解决数据倾斜问题而设计的一种优化机制。数据倾斜是指在分布式计算中,由于某些 key 具有大量数据,而其他 key 数据较少,导致某些分区的数据量特别大,造成计算负载不均衡。数据倾斜会导致个别节点出现性能…...

讯飞星火编排创建智能体学习(一)最简单的智能体构建
目录 开篇 智能体的概念 编排创建智能体 创建第一个智能体 编辑 大模型节点 测试与调试 开篇 前段时间在华为全联接大会上看到讯飞星火企业级智能体平台的演示,对于拖放的可视化设计非常喜欢,刚开始以为是企业用户才有的,回来之后查…...
mac-m1安装nvm,docker,miniconda
1.安装minicondaMAC OS(M1)安装配置miniconda_mac-mini m1 conda-CSDN博客 2.安装nvm(用第二个方法)Mac电脑安装nvm(node包版本管理工具)-CSDN博客 3.安装docker dmg下载链接docker-toolbox-mac-docker-for-mac安装包下载_开源镜像站-阿里云 教程MacOS系…...

STM32F407之Flash
寄存器分类 一般寄存器分为只读存储器 (ROM) 随机存储器(RAM) 只读存储器 只读存储器也被称为ROM 在正常工作时只能读不能写。 只读存储器经历的阶段 ROM->PROM->EPROM->EEPROM ->Flash 优点:掉电不丢失,解构简单 缺点:只适…...
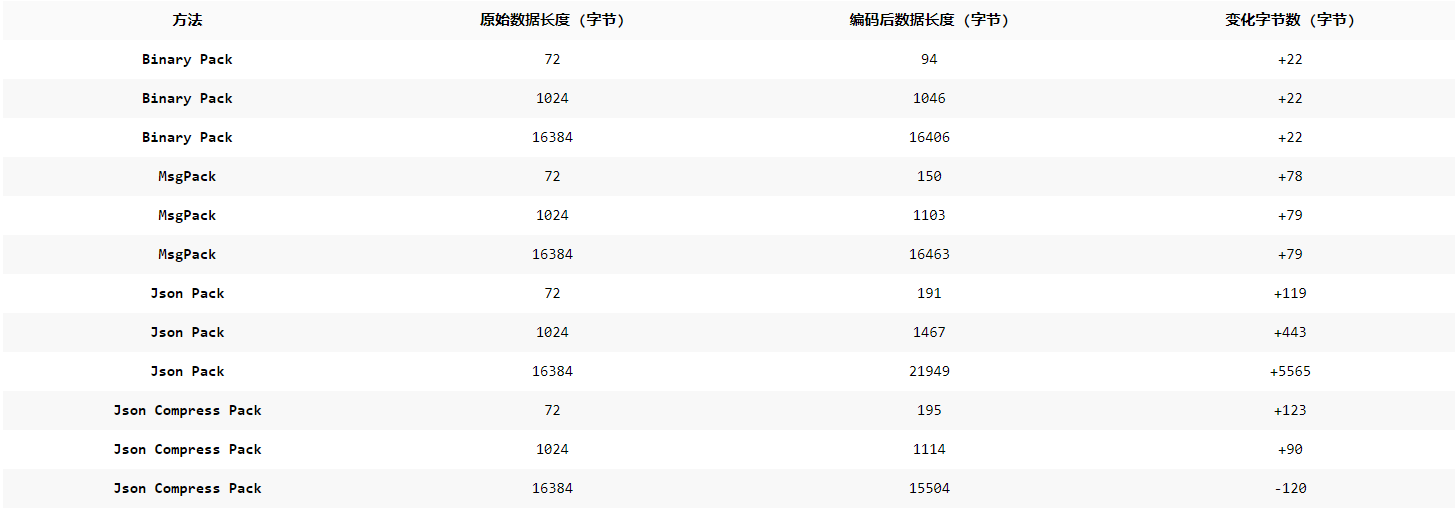
优化 Go 语言数据打包:性能基准测试与分析
场景:在局域网内,需要将多个机器网卡上抓到的数据包同步到一个机器上。 原有方案:tcpdump -w 写入文件,然后定时调用 rsync 进行同步。 改造方案:使用 Go 重写这个抓包逻辑及同步逻辑,直接将抓到的包通过网…...

【SQL】未订购的客户
目录 语法 需求 示例 分析 代码 语法 SELECT columns FROM table1 LEFT JOIN table2 ON table1.common_field table2.common_field; LEFT JOIN(或称为左外连接)是SQL中的一种连接类型,它用于从两个或多个表中基于连接条件返回左表…...

Qt(9.28)
widget.cpp #include "widget.h"Widget::Widget(QWidget *parent): QWidget(parent) {QPushButton *btn1 new QPushButton("登录",this);this->setFixedSize(640,480);btn1->resize(80,40);btn1->move(200,300);btn1->setIcon(QIcon("C:…...

javascript-冒泡排序
前言:好久没学习算法了,今天看了一个视频课,之前掌握很好的冒泡排序居然没写出来? <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport"…...

第九届蓝桥杯嵌入式省赛程序设计题解析(基于HAL库)
一.题目分析 (1).题目 (2).题目分析 按键功能分析----存储位置的切换键 a. B1按下切换存储位置,切换后定时时间设定为当前位置存储的时间 b. B2短按切换时分秒高亮,设置完成后,长按把设置的时…...

MATLAB云计算集成:在云端扩展计算能力
摘要 MATLAB云计算集成是指将MATLAB的计算能力与云平台的弹性资源相结合,以实现高性能计算、数据处理和算法开发。本文详细介绍了MATLAB云计算的基本概念、优势、配置要点以及编程实践。 1. 云计算概述 云计算是一种通过互联网提供计算资源(如服务器、…...

基于BeagleBone Black的网页LED控制功能(flask+gpiod)
目录 项目介绍硬件介绍项目设计开发环境功能实现控制LED外设构建Webserver 功能展示项目总结 👉 【Funpack3-5】基于BeagleBone Black的网页LED控制功能 👉 Github: EmbeddedCamerata/BBB_led_flask_web_control 项目介绍 基于 BeagleBoard Black 开发板…...

【C语言】单片机map表详细解析
1、RO Size、RW Size、ROM Size分别是什么 首先将map文件翻到最下面,可以看到 1.1 RO Size:只读段 Code:程序的代码部分(也就是 .text 段),它存放了程序的指令和可执行代码。 RO Data:只读…...

Java中的继承和实现
Java中的继承和实现在面向对象编程中扮演着不同的角色,它们之间的主要区别可以从以下几个方面进行阐述: 1. 定义和用途 继承(Inheritance):继承是面向对象编程中的一个基本概念,它允许我们定义一个类&…...

uniapp云打包
ios打包 没有mac电脑,使用香蕉云编 先登录香蕉云编这个工具,新建csr文件——把csr文件下载到你电脑本地: 然后,登录苹果开发者中心 生成p12证书 1、点击+号创建证书 创建证书的时候一定要选择ios distribution app store and ad hoc类型的证书 2、上传刚才从本站生成的…...

端口安全技术原理与应用
目录 概述 端口安全原理 端口安全术语 二层安全地址配置 端口模式下配置 全局模式下配置 动态学习 二层数据包处理流程 三层安全地址配置 三层数据包处理流程 端口安全违例动作和安全地址老化时间 查看命令 端口安全的注意事项 小结 概述 园区网的接入安全关系着…...

数据集-目标检测系列-鲨鱼检测数据集 shark >> DataBall
数据集-目标检测系列-鲨鱼检测数据集 shark >> DataBall 数据集-目标检测系列-鲨鱼检测数据集 shark 数据量:6k 数据样例项目地址: gitcode: https://gitcode.com/DataBall/DataBall-detections-100s/overview github: https://github.com/Te…...

数字乡村解决方案-3
1. 国家大数据战略与数字乡村 中国第十三个五年规划纲要强调实施国家大数据战略,加快建设数字中国,推进数据资源整合和开放共享,保障数据安全,以大数据助力产业转型升级和提高社会治理的精准性与有效性。 2. 大数据与数字经济 …...

WPF文本框无法输入小数点
问题描述 在WPF项目中,文本框BInding双向绑定了数据Text“{UpdateSourceTriggerPropertyChanged}”,但手套数据是double类型,手动输入数据时,小数点输入不进去 解决办法: 在App.xaml.cs文件中添加语句: …...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
