深入探索机器学习中的目标分类算法
在当今数据驱动的世界中,机器学习(Machine Learning, ML)正逐渐成为解决问题的重要工具。在众多机器学习任务中,目标分类(Classification)算法尤其受到关注。本文将深入探讨目标分类算法的基本概念、常见类型、应用场景以及实际案例,帮助读者全面理解这一重要主题。
一、什么是目标分类?
目标分类是机器学习中的一种监督学习任务,其目标是根据输入数据的特征将数据点分配到预定义的类别中。与回归任务不同,分类任务的输出是离散的标签。例如,在垃圾邮件检测中,电子邮件被分为“垃圾邮件”或“非垃圾邮件”。

二、常见目标分类算法
1. 逻辑回归(Logistic Regression)

逻辑回归是一种广泛使用的线性分类算法,虽然名字中有“回归”二字,但它主要用于分类任务。逻辑回归的核心思想是利用逻辑函数(Sigmoid函数)将线性组合的输入特征映射到0到1之间的概率值。通过设定一个阈值(通常为0.5),可以将概率值转化为类别标签。
数学原理: 逻辑回归的目标是找到一个最佳的线性模型,形式为: [ P(Y=1|X) = \frac{1}{1 + e^{-(\beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_nX_n)}} ] 其中,(Y)是目标变量,(X)是特征,(\beta)是模型参数。
优缺点:
- 优点:易于实现和解释,适合处理线性可分的数据,计算效率高。
- 缺点:对特征的线性假设较强,处理非线性数据时效果较差,容易受到异常值的影响。
应用案例:在客户流失预测中,可以使用逻辑回归分析客户的使用时长、购买频率等特征,预测客户是否会流失。
2. 支持向量机(Support Vector Machine, SVM)

支持向量机是一种强大的分类算法,尤其在处理高维数据时表现优异。SVM试图在不同类别之间找到一个最优的超平面,使得各类别之间的间隔最大化。支持向量机不仅可以处理线性可分的问题,还可以通过引入核函数(Kernel Trick)处理非线性问题。
核心概念:
- 超平面:在特征空间中划分不同类别的边界。
- 支持向量:离超平面最近的样本点,它们对超平面的构建起到关键作用。
优缺点:
- 优点:在高维空间中表现良好,能够有效处理非线性数据,且不容易过拟合。
- 缺点:对参数选择和核函数的选择敏感,计算复杂度较高,训练时间较长。
应用案例:在文本分类中,SVM可以有效区分垃圾邮件和正常邮件。通过将文本数据转换为特征向量,SVM能够找到最佳的分类边界。
3. 决策树(Decision Tree)

决策树是一种基于树形结构的分类算法,通过对特征进行条件判断来进行分类。每个内部节点代表一个特征,每个分支代表特征的一个取值,而每个叶子节点代表最终的分类结果。决策树的构建通常采用贪心算法,选择最能区分数据的特征进行分裂。
关键指标:
- 信息增益:用于衡量特征对分类的贡献。
- 基尼指数:衡量样本的纯度,值越小表示样本越纯。
优缺点:
- 优点:易于理解和可视化,能够处理非线性关系,适用于类别型和数值型特征。
- 缺点:容易过拟合,尤其是在树深度较大时,且对噪声敏感。
应用案例:在客户信用评分中,决策树可以通过客户的收入、信用历史、贷款情况等特征,逐步分裂出客户的信用等级。
4. 随机森林(Random Forest)

随机森林是集成学习的一种方法,通过构建多个决策树并结合它们的预测结果来提高分类性能。每棵树都是在随机选择的特征子集上训练的,最终通过投票机制决定输出类别。这种方法有效降低了过拟合的风险,提高了模型的鲁棒性。
优缺点:
- 优点:抗过拟合能力强,能够处理高维特征,适应性强。
- 缺点:模型较大,不易于解释,训练和预测时间较长。
应用案例:在医疗领域,随机森林可以用于疾病预测,通过综合患者的多项健康指标(如血压、胆固醇水平等)来判断其患病风险。
5. 神经网络(Neural Networks)
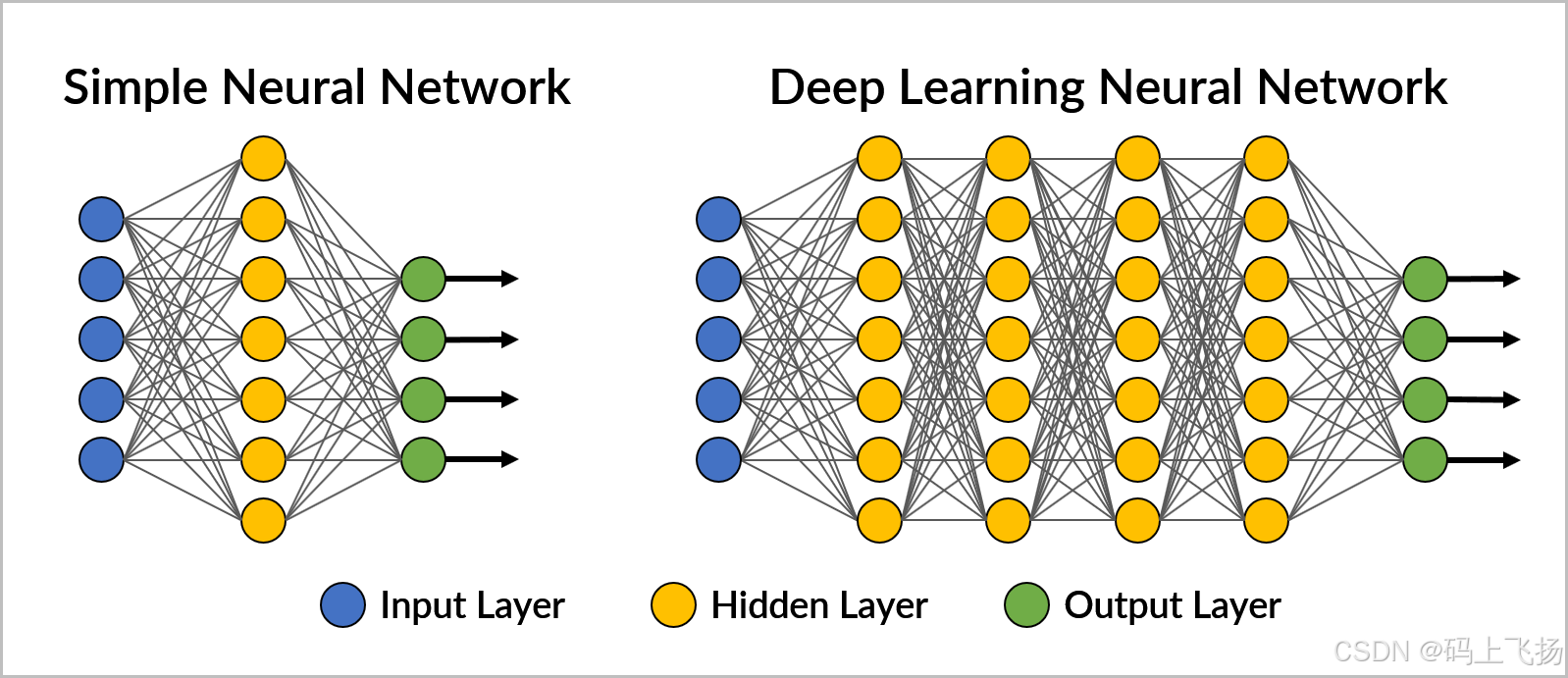
神经网络是一种模拟人脑神经元连接的分类算法,能够通过多层次的非线性变换来学习复杂的模式。常见的神经网络结构包括全连接网络、卷积神经网络(CNN)和循环神经网络(RNN)。其中,CNN在图像分类任务中表现尤为突出,RNN则在序列数据处理(如文本和时间序列)中应用广泛。
工作原理:
- 前向传播:输入数据经过每一层的加权和激活函数处理,最终输出结果。
- 反向传播:通过计算损失函数的梯度,更新网络参数,以最小化预测误差。
优缺点:
- 优点:能够自动提取特征,适合处理复杂的非线性关系,具有较强的泛化能力。
- 缺点:训练时间较长,参数调整复杂,对数据量和计算资源要求高。
应用案例:在自动驾驶中,卷积神经网络被广泛应用于识别道路标志和行人,从而实现安全的自动驾驶决策。
三、如何选择合适的分类算法?
选择合适的分类算法通常取决于以下几个因素:
- 数据规模:小数据集适合逻辑回归和决策树,大数据集可以考虑随机森林和神经网络。
- 特征类型:数值型特征适合逻辑回归和SVM,类别型特征则更适合决策树。
- 模型解释性:如果需要可解释性,决策树和逻辑回归是较好的选择;若不需要,则可以使用随机森林和神经网络。
- 计算资源:神经网络通常需要更多的计算资源,而逻辑回归和决策树相对较轻。
四、算法性能比较
在选择目标分类算法时,了解不同算法的性能是至关重要的。以下是从多个角度对常见分类算法进行比较,包括准确率、训练时间、可解释性、抗过拟合能力和适用场景。我们通过表格的方式来清晰地展示这些特征。
性能比较维度
- 准确率(Accuracy):指模型在测试集上正确分类的比例。
- 训练时间(Training Time):算法在训练模型上所需的时间。
- 可解释性(Interpretability):模型的决策过程是否容易理解。
- 抗过拟合能力(Overfitting Resistance):模型在新数据上的泛化能力。
- 适用场景(Use Cases):算法适合解决的问题类型。
算法性能比较表
| 分类算法 | 准确率 | 训练时间 | 可解释性 | 抗过拟合能力 | 适用场景 |
|---|---|---|---|---|---|
| 逻辑回归 | 中等 | 快速 | 高 | 较低 | 二分类问题,线性可分数据 |
| 支持向量机 | 高 | 中等 | 中 | 中等 | 文本分类,图像识别 |
| 决策树 | 中等 | 快速 | 高 | 较低 | 分类问题,医疗诊断 |
| 随机森林 | 高 | 中等 | 中 | 高 | 特征较多的复杂数据 |
| 神经网络 | 最高 | 较长 | 低 | 高 | 图像处理,语音识别,复杂模式 |
详细分析
-
准确率:
- 逻辑回归和决策树在简单线性可分数据上表现良好,但在复杂数据上可能不如支持向量机和随机森林。神经网络在处理大量数据时能达到最高的准确率,但需要适当的调参。
-
训练时间:
- 逻辑回归和决策树训练时间较短,适合快速实验。神经网络的训练时间较长,尤其是在大数据集上。
-
可解释性:
- 逻辑回归和决策树具有较高的可解释性,决策过程清晰。而神经网络由于其复杂的结构,通常被认为是“黑箱”模型,较难解释其决策过程。
-
抗过拟合能力:
- 随机森林和神经网络在抗过拟合能力上表现优异,尤其在处理高维数据时。相对而言,逻辑回归和决策树容易过拟合。
-
适用场景:
- 各算法适用的场景有所不同,逻辑回归适合线性可分问题,支持向量机在文本和图像分类中表现突出,随机森林适用于特征较多的复杂数据,而神经网络则在处理图像、语音等复杂模式时表现最佳。
通过上述比较,您可以根据具体的需求和数据特征,选择最适合的分类算法。希望这一章节能够为您在算法选择上提供有价值的参考!如果您有进一步的问题或想法,欢迎在评论区讨论。
五、结论
目标分类算法在机器学习中扮演着至关重要的角色。通过理解不同算法的特点、应用场景及其优势,您可以更好地选择适合您需求的算法。随着数据量的不断增加和计算能力的提升,目标分类算法的应用将更加广泛,为各行各业带来更多的创新和变革。
相关文章:

深入探索机器学习中的目标分类算法
在当今数据驱动的世界中,机器学习(Machine Learning, ML)正逐渐成为解决问题的重要工具。在众多机器学习任务中,目标分类(Classification)算法尤其受到关注。本文将深入探讨目标分类算法的基本概念、常见类…...
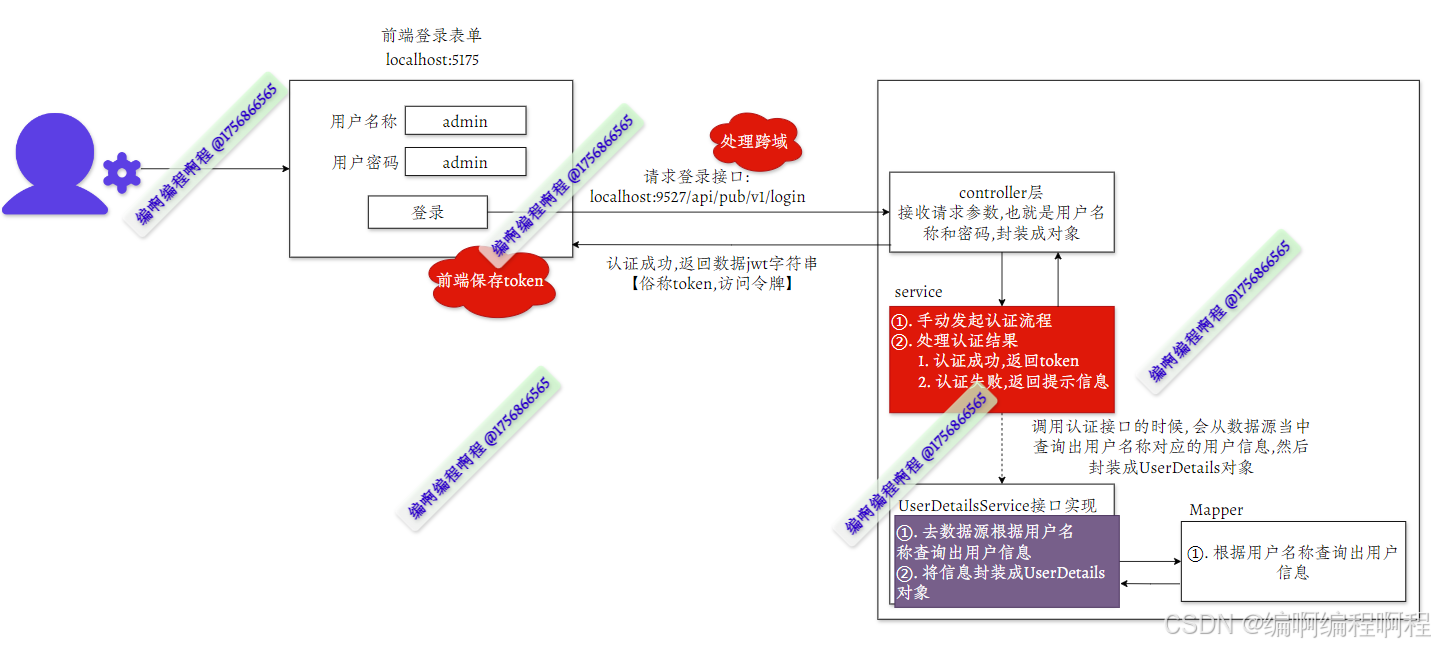
一文上手SpringSecurity【七】
之前我们在测试的时候,都是使用的字符串充当用户名称和密码,本篇将其换成MySQL数据库. 一、替换为真实的MySQL 1.1 引入依赖 <dependency><groupId>mysql</groupId><artifactId>mysql-connector-java</artifactId><version>8.0.33</v…...

深圳龙链科技:全球区块链开发先锋,领航Web3生态未来
【深圳龙链科技】是全球领先的Web3区块链技术开发公司,专注于为全球客户提供创新高效的区块链解决方案。 深圳龙链科技由币安资深股东携手香港领先的Web3创新枢纽Cyberport联袂打造,立足于香港这一国际金融中心,放眼全球,汇聚了华…...

手写代码,利用 mnist 数据集测试对比 kan 和 cnn/mlp 的效果
你好呀,我是董董灿。 kan 模型火了一段时间,很多人从理论的角度给出了非常专业的解读,基本结论是:从目前来看,kan 很难替代 mlp 成为一个更加经典的模型结构。 我这里就不从理论方面进行回答了,直接给出一…...

基于Java+SQL Server2008开发的(CS界面)个人财物管理系统
一、需求分析 个人财务管理系统是智能化简单化个人管理的重要的组成部分。并且随着计算机技术的飞速发展,计算机在管理方面应用的旁及,利用计算机来实现个人财务管理势在必行。本文首先介绍了个人财务管理系统的开发目的,其次对个人财务管理…...

15年408计算机网络
第一题: 解析: 接收方使用POP3向邮件服务器读取邮件,使用的TCP连接,TCP向上层提供的是面向连接的,可靠的数据传输服务。 第二题: 解析:物理层-不归零编码和曼彻斯特编码 编码1:电平在…...

C++ const关键字
const 1. 修饰变量(包括函数参数 函数返回值) const int v0 10; v0 0; // error 不能修改const修饰的变量 2. 修饰指针 int v1 10; int v2 20; int v3 30; 2.1 常量指针 const 在指针左边,左定值,即不能通过指针修改该…...
python爬虫案例——腾讯网新闻标题(异步加载网站数据抓取,post请求)(6)
文章目录 前言1、任务目标2、抓取流程2.1 分析网页2.2 编写代码2.3 思路分析前言 本篇案例主要讲解异步加载网站如何分析网页接口,以及如何观察post请求URL的参数,网站数据并不难抓取,主要是将要抓取的数据接口分析清楚,才能根据需求编写想要的代码。 1、任务目标 目标网…...

LeetCode416:分割等和子集
题目链接:416. 分割等和子集 - 力扣(LeetCode) 代码如下: class Solution { public:bool canPartition(vector<int>& nums) {int m nums.size();vector<int> dp(10010, 0);int sum 0;for(int i 0; i < m;…...

自定义异常注解处理框架
首先我们定义两个用于检验string和List的注解 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/*** author caiyi.yu* 自定义非空判断*/ Target(Elemen…...
【小程序】微信小程序课程 -3 快速上手之常用方法
目录 1、 对话框 1.1 模态对话框 1.2 消息对话框 2、 存储 2.1 同步 2.1.1 同步保存数据 2.1.2 同步获取数据 2.1.3 同步删除数据 2.1.4 同步清空数据 2.2 异步 2.2.1 异步保存数据 2.2.2 异步获取数据 2.2.3 异步删除数据 2.2.4 异步清空数据 3、 上拉加载更多…...
iOS 小组件
基本知识 时间轴 小组件通过AppIntentTimelineProvider进行 UI 刷新 struct Provider: AppIntentTimelineProvider {func placeholder(in context: Context) -> SimpleEntry {// 添加占位的(选择添加的时候使用)// todo}func snapshot(for configu…...
【2.使用VBA自动填充Excel工作表】
目录 前言什么是VBA如何使用Excel中的VBA简单基础入门控制台输出信息定义过程(功能)定义变量常用的数据类型Set循环For To 我的需求开发过程效果演示文件情况测试填充源文件测试填充目标文件 全部完整的代码sheet1中的代码,对应A公司工作表Us…...
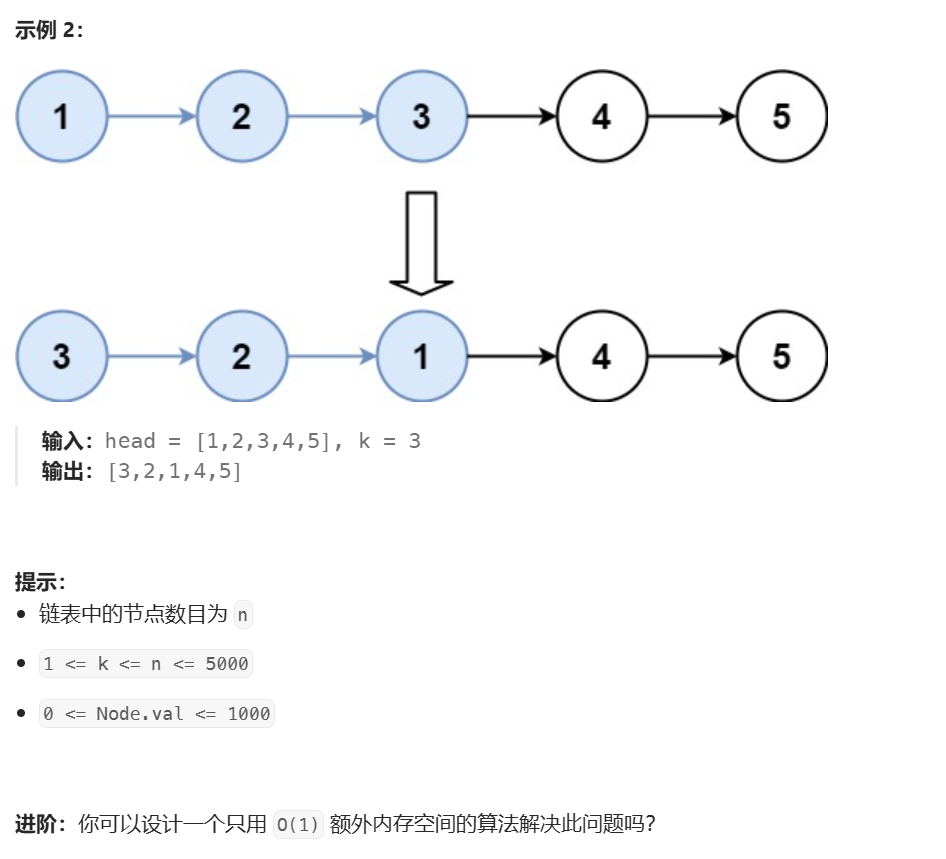
算法记录——链表
2.链表 2.1判断是否是回文链表 1.方法一:利用栈反转链表 /*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val val; }* ListNode(int val, ListNode…...

EasyExcel实现百万数据批量导出
当数据量比较大时,例如数据量达到百万级,传统的一次读取到内存中在写入excel文件的方法便不再适用了,可能会导致内存溢出;而且一次性将数据写入一张sheet工作表也不太好。 但我们可以选择数据分片的方式批量写入多个工作表。 测试…...

兆易GD32E508的SHRTIM配置 主从定时器 产生2对相位可调互补PWM 带死区
如有技术问题及技术需求请加作者微信! GD32E5系列MCU是基于Arm Cortex-M33处理器的32位通用微控制器。Cortex-M33处理器基于Armv8架构,处理器主频最高可达180MHz,支持强大的可扩展指令集,包括通用数据处理I/O控制任务、增强的数据处理位域操作、DSP和浮点运算器(FPU)。 GD…...

数据归组工具
利用C#将数据 [ {"name":"A","fzh":1}, {"name":"A","fzh":2}, {"name":"A","fzh":3}, {"name":"B","fzh":4}, {"name":"B",&…...

JavaScript 中的闭包的形成及使用场景
JavaScript 中的闭包 闭包(Closure) 是 JavaScript 中一个非常重要且独特的概念,它指的是 函数能够记住并访问其词法作用域内的变量,即使这个函数在其词法作用域之外执行。 通俗地说,闭包是 一个函数可以“记住”它在…...

后端返回内容有换行标识,前端如何识别换行
<br/>的话 用 v-html \n 可以用css样式 white-space: pre-wrap 后端返回结果 前端...

服务器被挂马,导致网站首页被更改怎么解决
当服务器被挂马并导致网站首页被篡改时,说明服务器或网站的安全性遭到破坏。为了修复并防止未来的攻击,你可以按照以下步骤进行操作: 1. 立即下线网站 目的:防止恶意软件进一步传播,保护用户数据和防止攻击者继续对网…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
