寻找两个正序数的中位数(C)
最近面试,发现要手撕算法加上机试,被完败,索性给自己立一个目标,一周训练2次。
第一题。
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2] 输出:2.00000 解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4] 输出:2.50000 解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
提示:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-10^6 <= nums1[i], nums2[i] <= 10^6
这题力扣第四题,我看着简单,内容还可以一下子接受.想了快三个小时。
double get_mid(int* nums,int numsSize)
{if(numsSize%2){return nums[numsSize/2];}else{return (nums[numsSize/2]+nums[(numsSize)/2-1])*1.0/2;}
}double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {if((nums1Size==0)&&(nums2Size==0)) return 0;else if((nums1Size==0)&&(nums2Size!=0)){return get_mid(nums2,nums2Size);}else if((nums2Size==0)&&(nums1Size!=0)){return get_mid(nums1,nums1Size);}else{if(nums1[nums1Size-1] <=nums2[0]){int len = nums1Size+nums2Size ;int mid_index = len /2;if(len % 2 ) // 长度是奇数{if(mid_index >= nums1Size){return nums2[nums2Size-mid_index-1];}else{return nums1[mid_index]*1.0;}}else //长度是偶数{if(mid_index < nums1Size){return (nums1[mid_index]+nums1[mid_index-1])*1.0/2;}else if((mid_index) == nums1Size){return (nums1[nums1Size-1]+nums2[0])*1.0/2;}else{return (nums2[nums2Size-mid_index-1]+nums2[nums2Size-mid_index])*1.0/2;}}}else if(nums2[nums2Size-1] <=nums1[0]){int len = nums1Size+nums2Size ;int mid_index = len /2;if(len % 2 ) //长度是奇数{if(mid_index >= nums2Size){return nums1[nums1Size-mid_index-1];}else{return nums2[mid_index];}}else //长度是偶数{if(mid_index < nums2Size){return (nums2[mid_index]+nums2[mid_index-1])*1.0/2;}else if((mid_index) == nums2Size){return (nums1[0]+nums2[nums2Size-1])*1.0/2;}else{return (nums1[nums1Size-mid_index-1]+nums1[nums1Size-mid_index])*1.0/2;}}}else{int len = nums1Size+nums2Size ;int mid_index = len /2;int count =0;int _n1 = 0,_n2=0;int last=0,midv=0;while(true){if(_n1 == nums1Size) {midv=nums2[_n2];count++;if(count == mid_index+1){if(len%2){return midv*1.0;}else{return (last+midv)*1.0/2;} }_n2++;last = midv;}else if(_n2 == nums2Size) {midv=nums1[_n1];count++;if(count == mid_index+1){if(len%2){return midv*1.0;}else{return (last+midv)*1.0/2;} }_n1++;last = midv;}else{if(nums1[_n1] >= nums2[_n2]){midv = nums2[_n2];count++;if(count == mid_index+1){if(len%2){return midv*1.0;}else{return (last+midv)*1.0/2;}}_n2++;last = midv;}else{midv = nums1[_n1];count++;if(count == mid_index+1){if(len%2){return midv;}else{return (last+midv)*1.0/2;}}_n1++;last = midv;}}}}}}写的很烂很长,就是没有做过算法题目的人的思维,用了很多特殊情况来提高运算速度,其实把最后一个else提取出来也可以进行运算。但不知道为什么内存消耗很高。
相关文章:
)
寻找两个正序数的中位数(C)
最近面试,发现要手撕算法加上机试,被完败,索性给自己立一个目标,一周训练2次。 第一题。 给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 …...

YOLOv10涨点改进:IoU优化 | Unified-loU,用于高品质目标检测的统一loU ,2024年8月最新IoU
💡💡💡现有IoU问题点:IoU (Intersection over Union)作为模型训练的关键,极大地显示了当前预测框与Ground Truth框之间的差异。后续研究者不断在IoU中加入更多的考虑因素,如中心距离、纵横比等。然而,仅仅提炼几何差异是有上限的;而且新的对价指数与借据本身存在潜在…...

Spring Boot 实现动态配置导出,同时支持公式和动态下拉框渲染和性能优化案例示范
在业务系统中,数据导出是一个非常常见且重要的功能,本文将详细介绍如何在 Spring Boot 中实现这一功能,并结合 MySQL 数据库、MyBatis 作为数据访问层,EasyExcel 作为导出工具,展示如何在电商交易系统中搭建灵活、可扩…...

一网打尽 运维必封的50个高危端口清单,零基础入门到精通,收藏这一篇就够了
文件传输相关端口: • TCP 20、21:FTP 服务(文件传输协议)端口,FTP 传输数据时未加密,容易受到攻击,如匿名上传下载、爆破、嗅探、远程执行等攻击,可能导致敏感文件泄露。 • TCP …...

方法 WebDriverWait
定义: WebDriverWait是Selenium WebDriver提供的一个工具类,它允许你设置等待条件,直到这个条件成立,才继续执行代码。这对于处理网页上的异步加载元素特别有用,比如等待某个元素变得可见、可点击等。 from se…...
)
LOESS(Locally Estimated Scatterplot Smoothing)
文章目录 LOESS 原理详解:LOESS 的优点:LOESS 的缺点:Python 实现代码:代码说明: LOESS(Locally Estimated Scatterplot Smoothing),即局部加权回归,是一种非参数回归方法…...
)
每天学习一个技术栈 ——【Django Channels】篇(1)
在当今快速发展的技术领域,掌握多种技术栈已经成为开发者提升竞争力的关键。随着实时应用需求的不断增加,如何高效地处理并发请求和实时通信变得尤为重要。在众多解决方案中,Django Channels作为Django框架的强大扩展,能够轻松实现…...

js设计模式-工厂模式 单例模式 观察者模式 发布订阅模式 原型模式 代理模式 迭代器模式
1 工厂模式 // 工厂模式: 调用函数返回对象function factory(name, age){return {name: name,age: age} }const person1 factory(Tom, 18); // 类似的库使用工厂函数的有: jQuery, React.createElement,axios.create,vue.createApp等 2 单例模式 // 单例模式:单…...

关于Java中的List<User>如何进行深拷贝
联调中发现了一个很初级,但有容易被忽略的拷贝问题: 错误方式:List<User> us new ArrayList<>(); // name "张三"List<User> us1 new ArrayList<>(us);for (User u : us) {...u.setName("douzi&q…...

2025 年 IT 前景:机遇与挑战并存,人工智能和云计算成重点
云计算de小白 投资人工智能:平衡潜力与实用性 到 2025 年,人工智能将成为 IT 支出的重要驱动力,尤其是在生成式人工智能领域。人工智能的前景在于它有可能彻底改变业务流程、增强决策能力并开辟新的收入来源。然而,现实情况更加微…...

Cortex-A7和Cortex-M7架构处理器取中断向量全流程分析
0 参考资料 Cortex M3权威指南(中文).pdf ARM Cortex-A(armV7)编程手册V4.0.pdf1 Cortex-A7和Cortex-M7处理器架构取中断向量全流程分析 1.1 什么是中断向量? 中断向量就是中断服务函数入口地址,例如我们发生了EXTI0中断,就需要执行EXT0中…...

MODELS 2024震撼续章:科技与可持续性的未来交响曲
MODELS 2024国际会议正如火如荼地进行着,每一天都充满了新的发现与启迪,每一场分享都是对技术前沿的一次深刻探索,更是对现实世界可持续性挑战的一次积极回应。现在让我们继续这场科技盛宴,看看小编为您精选几场的学术分享吧~ 会议…...

CICD 持续集成与持续交付
一 、CICD是什么 CI/CD 是指持续集成(Continuous Integration)和持续部署(Continuous Deployment)或持续交付(Continuous Delivery) 1.1 持续集成(Continuous Integration) 持续集…...
是指负责实际数据处理和转发的部分)
“数据面”(Data Plane)是指负责实际数据处理和转发的部分
在计算机网络和服务架构中,“数据面”(Data Plane)是指负责实际数据处理和转发的部分。数据面负责执行具体的网络通信任务,如接收、处理和转发数据包。与数据面对应的是“控制面”(Control Plane)ÿ…...

面试题:MySQL你用过WITH吗?领免费激活码
感谢Java面试教程的Java多线程文章,点击查看>原文 Java面试教程,发mmm116可获取IDEA-jihuoma 在MySQL中,WITH子句用于定义临时表或视图,也称为公共表表达式(CTE)。它允许你在一个查询中定义一个临时结果…...

consul 介绍与使用,以及spring boot 项目的集成
目录 前言一、Consul 介绍二、Consul 的使用三、Spring Boot 项目集成 Consul总结前言 提示:这里可以添加本文要记录的大概内容: 例如:随着人工智能的不断发展,机器学习这门技术也越来越重要,很多人都开启了学习机器学习,本文就介绍了机器学习的基础内容。 提示:以下是…...

Linux常用命令shell常用知识 。。。。面试被虐之后,吐血整理。。。。
Linux三剑客&常用命令&shell常识 Linux三剑客grep - print lines matching a patternsed - stream editor for filtering and transforming textawkman awk Linux常用命令dd命令ssh命令tar命令curl命令top命令tr命令xargs命令sort命令du/df/free命令 shell 知识functio…...

压力测试指南-压力测试基础入门
压力测试基础入门 在当今快速迭代的软件开发环境中,确保应用程序在高负载情况下仍能稳定运行变得至关重要。这正是压力测试大显身手的时刻。本文将带领您深入了解压力测试的基础知识,介绍实用工具,并指导您设计、执行压力测试,最…...

Linux:LCD驱动开发
目录 1.不同接口的LCD硬件操作原理 应用工程师眼中看到的LCD 1.1像素的颜色怎么表示 编辑 1.2怎么把颜色发给LCD 驱动工程师眼中看到的LCD 统一的LCD硬件模型 8080接口 TFTRGB接口 什么是MIPI Framebuffer驱动程序框架 怎么编写Framebuffer驱动框架 硬件LCD时序分析…...

QT:常用类与组件
1.设计QQ的界面 widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QPushButton> #include <QLineEdit> #include <QLabel>//自定义类Widget,采用public方式继承QWidget,该类封装了图形化界面的相关操作ÿ…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...
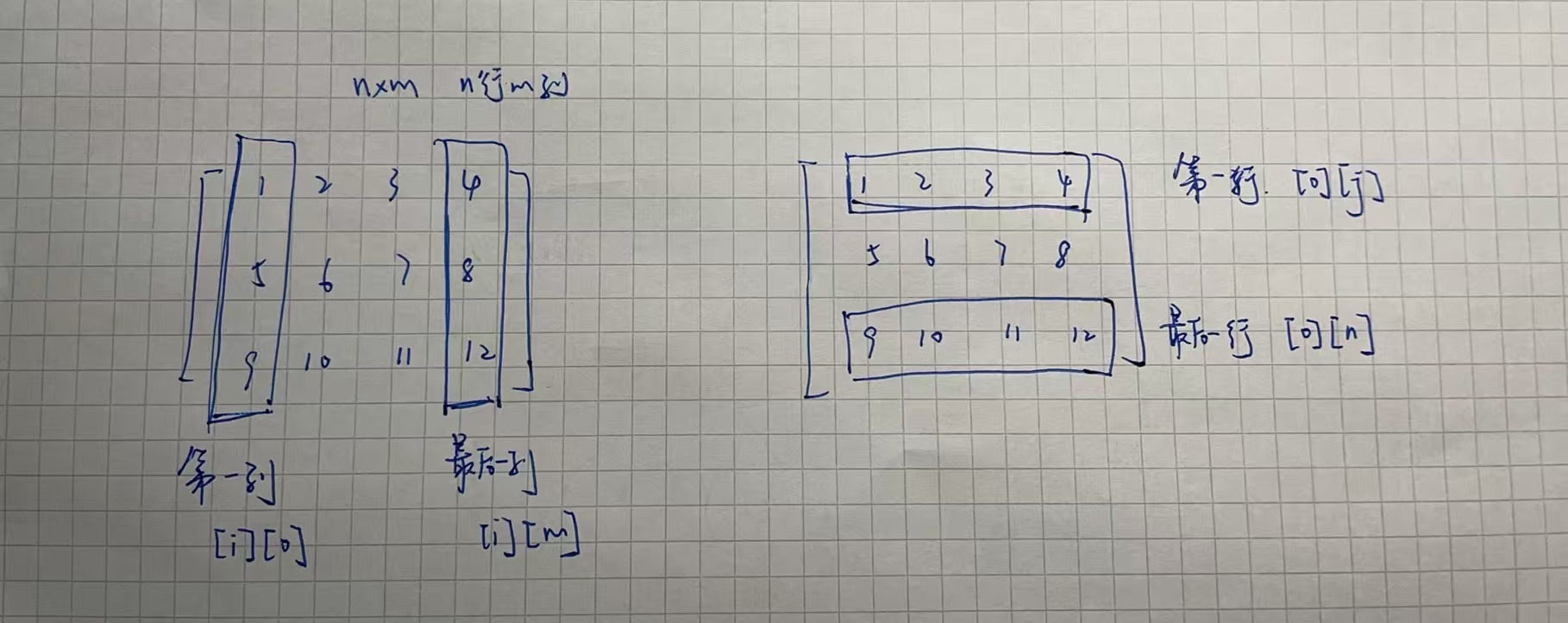
二维数组 行列混淆区分 js
二维数组定义 行 row:是“横着的一整行” 列 column:是“竖着的一整列” 在 JavaScript 里访问二维数组 grid[i][j] 表示 第i行第j列的元素 let grid [[1, 2, 3], // 第0行[4, 5, 6], // 第1行[7, 8, 9] // 第2行 ];// grid[i][j] 表示 第i行第j列的…...

LeetCode 0386.字典序排数:细心总结条件
【LetMeFly】386.字典序排数:细心总结条件 力扣题目链接:https://leetcode.cn/problems/lexicographical-numbers/ 给你一个整数 n ,按字典序返回范围 [1, n] 内所有整数。 你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。…...
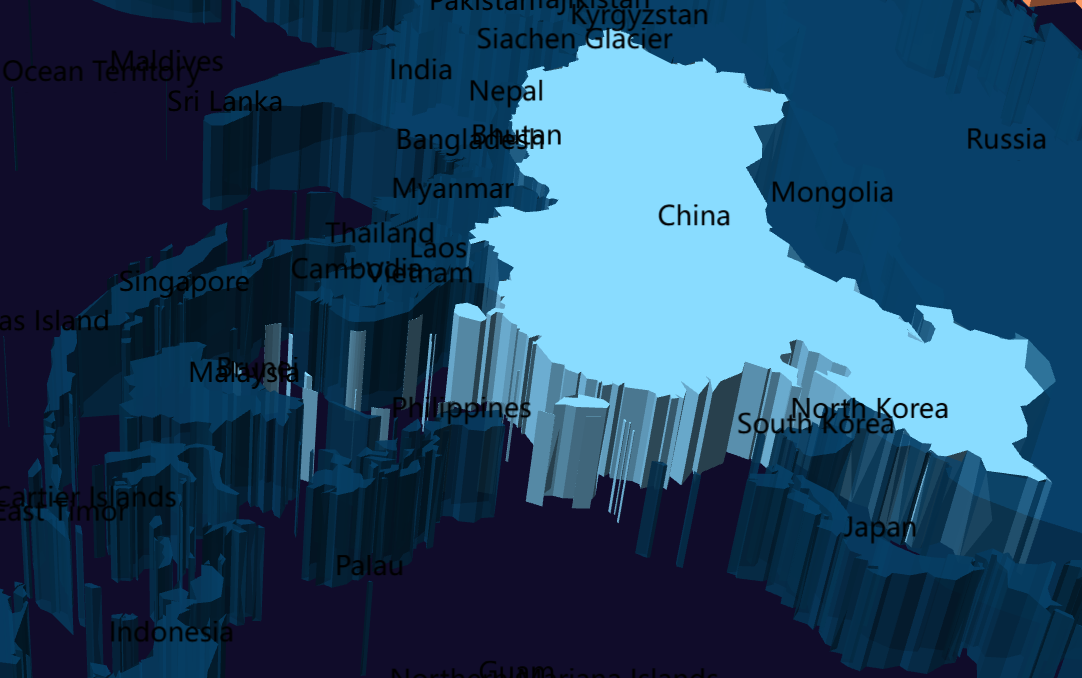
数据可视化交互
目录 【实验目的】 【实验原理】 【实验环境】 【实验步骤】 一、安装 pyecharts 二、下载数据 三、实验任务 实验 1:AQI 横向对比条形图 代码说明: 运行结果: 实验 2:AQI 等级分布饼图 实验 3:多城市 AQI…...
