分治(归并排序)
一、基本思路
我们以一个归并排序为例。
. - 力扣(LeetCode)

归并排序的思想:得到两个有序数组,把两个有序数组合并,传到下一层递归,一直得到两个有序数组,一直合并,最后就能得到有序数组。
那其实有许多问题需要解释:
1、如何得到两个有序数组,一开始可都是乱序啊
一个数组一直被一分为二,最后是不是就会被分成一个数组里面就一个元素?一个元素不就有序了。
那么一旦我们有了两个有序数组,合并两个有序数组之后的大有序数组随递归传到上一层是不是就作为了一个有序数组,和另外一层递归上来的有序数组就可以再次合并,直到递归结束,数组就被排序完成了。
2、如何理解在函数最开始写上“mergeSort(left, mid, nums); mergeSort(mid + 1, right, nums);” 就可以认为接下来是排好序的两个有序数组呢?
因为在这两个语句之前所有的递归都是在做mergeSort(left, mid, nums); mergeSort(mid + 1, right, nums);这两个语句的左右数组排序,传递到这一层的递归就是左右有序的两个数组。
所以我认为的归并排序本质:就是把一个数组在中间劈开,然后交给下一层递归,一直把一段数组一分为二,直到一个数组里面只有一个,这时满足两个数组有序,开始回溯,合并两个有序数组后向上交付数组。
二、例题
1、逆序对
. - 力扣(LeetCode)

思路:我们得到一个数组,以mid为中心,在左边挑一下逆序对个数(不就是把左边看成一个数组,得到递归的结果),在右边挑一下逆序对个数,最后得到两个有序数组之后用一下两种方式调一下左右数组里面的逆序对。

但是上面代码中我递增归并一开始写成了 ans += cur2 - mid - 1,其实这是错的,错因是我在要cur2移动的情况下用右边的数组来统计逆序对个数是错的,因为没有判断左边的情况,所以这种题如果移动cur1就要以右边数组作为基准,移动cur2要以左边数组作为基准。
2、翻转对
. - 力扣(LeetCode)

思路:和上一题非常类似,但是注意由于不是1:1的关系,不能把计算结果的过程和排序混在一起,必须先是计算结果,再排序。
3、计算右侧小的元素个数
. - 力扣(LeetCode)

思路:和逆序对思路一样,只不过要注意由于是返回数组,我们必须记录原来数组中的值与下标的对应关系,但是请注意不能用哈希表记录,因为原数组会有重复,导致键值重复,所以只能用index数组对应值,值移动,index数组也移动。
相关文章:

分治(归并排序)
一、基本思路 我们以一个归并排序为例。 . - 力扣(LeetCode) 归并排序的思想:得到两个有序数组,把两个有序数组合并,传到下一层递归,一直得到两个有序数组,一直合并,最后就能得到有…...

小学生为什么要学英语
小学生需要学习英语的原因有很多,以下是其中的一些原因(毕竟我也会累滴(* ̄▽ ̄*)): 1. 全球化交流:英语是国际交流的通用语言,学习英语可以帮助小学生更好地融入全球化的社会环境&am…...

企业云存储如何收费?企业云存储收费标准
企业云存储如何收费?企业云存储的收费方式因不同的服务提供商和具体的服务选项而异,通常从用户数量、存储容量、功能、混合收费、按需定价、定制化、功能模块等多个方面进行考量。以下是对其多方面收费方式的详细介绍: 1.按用户数量收费 适用…...

一步步教你LangGraph Studio:可视化调试基于LangGraph构建的AI智能体
之前我们在第一时间介绍过使用LangChain的LangGraph开发复杂的RAG或者Agent应用,随着版本的迭代,LangGraph已经成为可以独立于LangChain核心,用于开发多步骤、面向复杂任务、支持循环的AI智能体的强大框架。 近期LangGraph推出了一个使得复杂…...

用SpringBoot打造先进的学科竞赛管理系统
1绪 论 1.1研究背景 当今时代是飞速发展的信息时代。在各行各业中离不开信息处理,这正是计算机被广泛应用于信息管理系统的环境。计算机的最大好处在于利用它能够进行信息管理。使用计算机进行信息控制,不仅提高了工作效率,而且大大的提高了其…...

Linux入门攻坚——34、nsswitch、pam、rsyslog和loganalyzer前端展示工具
nsswitch:network service switch 名称解析:name <---> id 认证服务:用户名、密码验证或token验证等 名称解析和认证服务都涉及查找位置,即保存在哪里。如linux认证,passwd、shadow,是在文件中&…...
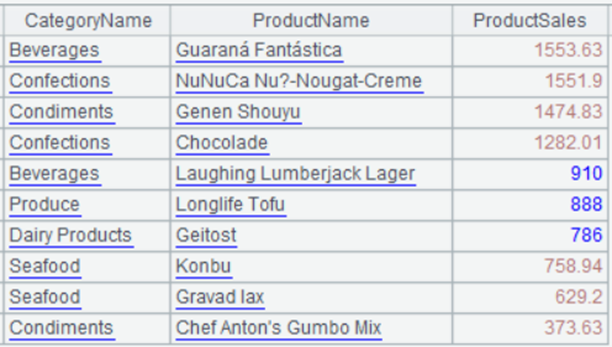
如何在Excel中快速找出前 N 名,后 N 名
有如下销售额统计表: 找出销售额排前 10 名的产品及其销售额,和销售额排倒数 10 名以内的产品及其销售额,结果如下所示: 前 10 名: spl("E(?1).sort(ProductSales:-1).to(10)",A1:C78)后 10 名࿱…...

创意实现!在uni-app小程序商品详情页轮播中嵌入视频播放功能
背景介绍 通过uni-app框架实现商城小程序商品详情页的视频与图片轮播功能,以提升用户体验和增加商品吸引力。通过展示商品视频和图片,用户可以更全面地了解商品细节,从而提高购买决策的便利性和满意度。这种功能适用于各类商品,如…...
WAF,全称Web Application Firewall,好用WAF推荐
WAF,全称Web Application Firewall,即Web应用防火墙,是一种网络安全设备,旨在保护Web应用程序免受各种Web攻击,如SQL注入、跨站脚本(XSS)、跨站请求伪造(CSRF)等。 WAF通…...

docker中搭建nacos并将springboot项目的配置文件转移到nacos中
前言 网上搜索docker中搭建nacos发现文章不是很好理解,正好最近在搭建nacos练手。记录一下整个搭建过程。文章最后附上了一些过程中遇到的问题,大家可以按需要查看。 docker中搭建nacos并将springboot项目的配置文件转移到nacos中 前言1 docker中下拉na…...

概率论原理
智慧挺不喜欢我,他告诉我需要有耐心,答案在后面;而我总想马上得到答案;但它也会给我奖励,因为我总会自己去寻找答案 B站 大大的小番茄 普林斯顿微积分 PDF 一化儿 BILIBILI 泰勒展开式 知乎https://www.zhihu.com…...

MYSQL的安装和升级
MySQL的RPM安装通常分为不同的包,包括Server、Common、Client、Devel、Libs、Libs-compat、Test、Source,请写出上述每个包的功能。 Server:包含MySQL服务器的核心文件和服务。安装此包后可以运行MySQL数据库服务器。 Common:包…...

深入解析 RISC-V 递归函数的栈使用:以阶乘函数为例
在处理递归函数时,RISC-V 体系架构的寄存器数量有限。为了确保每次递归调用能正确保存和恢复寄存器的状态,栈(stack)提供了灵活的解决方案。本文将结合具体的汇编代码和递归的阶乘函数 fact 来讲解 RISC-V 中如何利用栈进行寄存器…...

【保研纪念】计算机保研经验贴——南大cs、复旦cs、中南cs
文章目录 一、个人情况二、经验总结三、夏令营情况1、南京大学计算机学院(5月31日-6月2日)2、复旦大学计算机学院(7月1日-7月4日)3、中南大学计算机学院(7月5日-7月7日)4、武汉大学计算机学院 四、预推免情…...

TopOn对话游戏魔客:2024移动游戏广告应如何突破?
TopOn对话游戏魔客:2024移动游戏广告应如何突破? 近年来,游戏广告投放的成本日益走高,ROI如何回正,素材如何创新等问题困扰着每一个广告主。在隐私政策的实施下,广告投放难度也在不断升级。 据data.ai发布…...

Chainlit集成LlamaIndex实现知识库高级检索(BM25全文检索器)
检索原理 BM25Retriever类是一个基于BM25算法设计的检索器,它主要用于从一组文档或节点中检索出与查询最相关的文档或节点。这个类的设计目的是为了提高文本检索的效率和准确性,尤其是在处理大量文本数据时。 BM25(Best Matching 25&#x…...

Dubbo入门案例
Dubbo 学习地址:Dubbo3 简介_w3cschool; 01-Dubbo入门案例 我们先来新建一个Dubbo的小案例来体验一下Dubbo的使用,我们先来创建一个springboot的项目。 1.1-zookeeper下载启动 在编写我们的入门案例之前,我们需要先去下…...

android设计模式的建造者模式,请举例
在Android开发中,建造者模式(Builder Pattern)是一种常用的设计模式,它主要用于构建复杂对象。建造者模式通过将复杂对象的构建与它的表示分离,使得同样的构建过程可以创建不同的表示。这种模式特别适用于那些需要多个…...

【探索智谱AI的CogVideoX:视频生成的新前沿】
2024年8月6日,智谱AI宣布其开源视频生成模型CogVideoX,激发了开发者的创造力和对新技术的期待。 一、CogVideoX模型概述 CogVideoX 是一款先进的视频生成工具,可基于最长 226 个 token 的提示生成视频,时长可达 6 秒,…...

ant design vue做表单验证及form表单外验证、父子嵌套多个表单校验
1、form表单验证(若有时遇到输入框有值但是还是触发验证规则了,请检查form表单绑定正确吗、校验规则正确吗、表格数据字段名正确吗) <a-form:model"formState":label-col"{ span: 8 }":wrapper-col"{ span: 16 }":rules"rul…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...
