哈希表题目:砖墙
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:砖墙
出处:554. 砖墙
难度
5 级
题目描述
要求
你的面前有一堵矩形的、由 n\texttt{n}n 行砖块组成的砖墙。这些砖块高度相同(也就是一个单位高)但是宽度不同。每一行砖块的宽度之和相等。
你现在要画一条自顶向下的、穿过最少砖块的垂线。如果你画的线只是从砖块的边缘经过,就不算穿过这块砖。你不能沿着墙的两个垂直边缘之一画线,这样显然是没有穿过一块砖的。
给你一个二维数组 wall\texttt{wall}wall,该数组包含这堵墙的相关信息。其中,wall[i]\texttt{wall[i]}wall[i] 是一个代表从左至右每块砖的宽度的数组。你需要找出怎样画才能使这条线穿过的砖块数量最少,并且返回穿过的砖块数量。
示例
示例 1:

输入:wall=[[1,2,2,1],[3,1,2],[1,3,2],[2,4],[3,1,2],[1,3,1,1]]\texttt{wall = [[1,2,2,1],[3,1,2],[1,3,2],[2,4],[3,1,2],[1,3,1,1]]}wall = [[1,2,2,1],[3,1,2],[1,3,2],[2,4],[3,1,2],[1,3,1,1]]
输出:2\texttt{2}2
示例 2:
输入:wall=[[1],[1],[1]]\texttt{wall = [[1],[1],[1]]}wall = [[1],[1],[1]]
输出:3\texttt{3}3
数据范围
- n=wall.length\texttt{n} = \texttt{wall.length}n=wall.length
- 1≤n≤104\texttt{1} \le \texttt{n} \le \texttt{10}^\texttt{4}1≤n≤104
- 1≤wall[i].length≤104\texttt{1} \le \texttt{wall[i].length} \le \texttt{10}^\texttt{4}1≤wall[i].length≤104
- 1≤sum(wall[i].length)≤2×104\texttt{1} \le \texttt{sum(wall[i].length)} \le \texttt{2} \times \texttt{10}^\texttt{4}1≤sum(wall[i].length)≤2×104
- 对于每一行 i\texttt{i}i,sum(wall[i])\texttt{sum(wall[i])}sum(wall[i]) 是相同的
- 1≤wall[i][j]≤231−1\texttt{1} \le \texttt{wall[i][j]} \le \texttt{2}^\texttt{31} - \texttt{1}1≤wall[i][j]≤231−1
解法
思路和算法
任意一条垂线在每一行都是穿过砖块或者从砖块的边缘经过,且穿过砖块的数量与从砖块的边缘经过的数量之和一定等于砖墙的行数 nnn。为了找到穿过最少砖块的垂线,应该找到经过最多的砖块边缘的垂线,砖墙的行数与该垂线经过的砖块边缘的数量之差即为穿过的砖块数量的最小值。
为了找到经过最多的砖块边缘的垂线,需要统计从砖墙左端开始的所有不同距离的砖块边缘的数量,并用哈希表记录所有距离对应的砖块边缘的数量。
对于砖墙的每一行,从左到右遍历每一块砖,并维护砖块宽度之和,砖块宽度之和即为当前砖块的右边缘与砖墙左端的距离。对于每一块砖,将其宽度加到砖块宽度之和中,并将更新后的砖块宽度之和在哈希表中的次数加 111。由于不能沿着墙的两个垂直边缘之一画线,因此每一行的最后一块砖不用遍历。
由于题目没有要求得到画线的位置,只要求得到穿过的砖块数量的最小值,因此在遍历结束砖墙的全部行之后,只需要从哈希表中得到砖块边缘数量的最大值,不需要得到砖块边缘与砖墙左端的距离。得到砖块边缘数量的最大值之后,计算砖墙的行数与砖块边缘数量的最大值之差,即为穿过的砖块数量的最小值。
代码
class Solution {public int leastBricks(List<List<Integer>> wall) {int n = wall.size();Map<Long, Integer> map = new HashMap<Long, Integer>();for (List<Integer> row : wall) {long sum = 0;int bricks = row.size();for (int i = 0; i < bricks - 1; i++) {sum += row.get(i);map.put(sum, map.getOrDefault(sum, 0) + 1);}}int maxCount = 0;Set<Map.Entry<Long, Integer>> entries = map.entrySet();for (Map.Entry<Long, Integer> entry : entries) {int count = entry.getValue();maxCount = Math.max(maxCount, count);}return n - maxCount;}
}
复杂度分析
-
时间复杂度:O(mn)O(mn)O(mn),其中 mmm 是砖墙每一行的平均砖块数量,nnn 是砖墙的行数。需要遍历砖墙中的每一行的除了最后一块砖的每块砖,并用哈希表记录每块砖的右边缘与砖墙左端的距离和次数。
-
空间复杂度:O(mn)O(mn)O(mn),其中 mmm 是砖墙每一行的平均砖块数量,nnn 是砖墙的行数。需要使用哈希表记录每一行的除了最后一块砖的每块砖的右边缘与砖墙左端的距离和次数。
相关文章:

哈希表题目:砖墙
文章目录题目标题和出处难度题目描述要求示例数据范围解法思路和算法代码复杂度分析题目 标题和出处 标题:砖墙 出处:554. 砖墙 难度 5 级 题目描述 要求 你的面前有一堵矩形的、由 n\texttt{n}n 行砖块组成的砖墙。这些砖块高度相同(…...
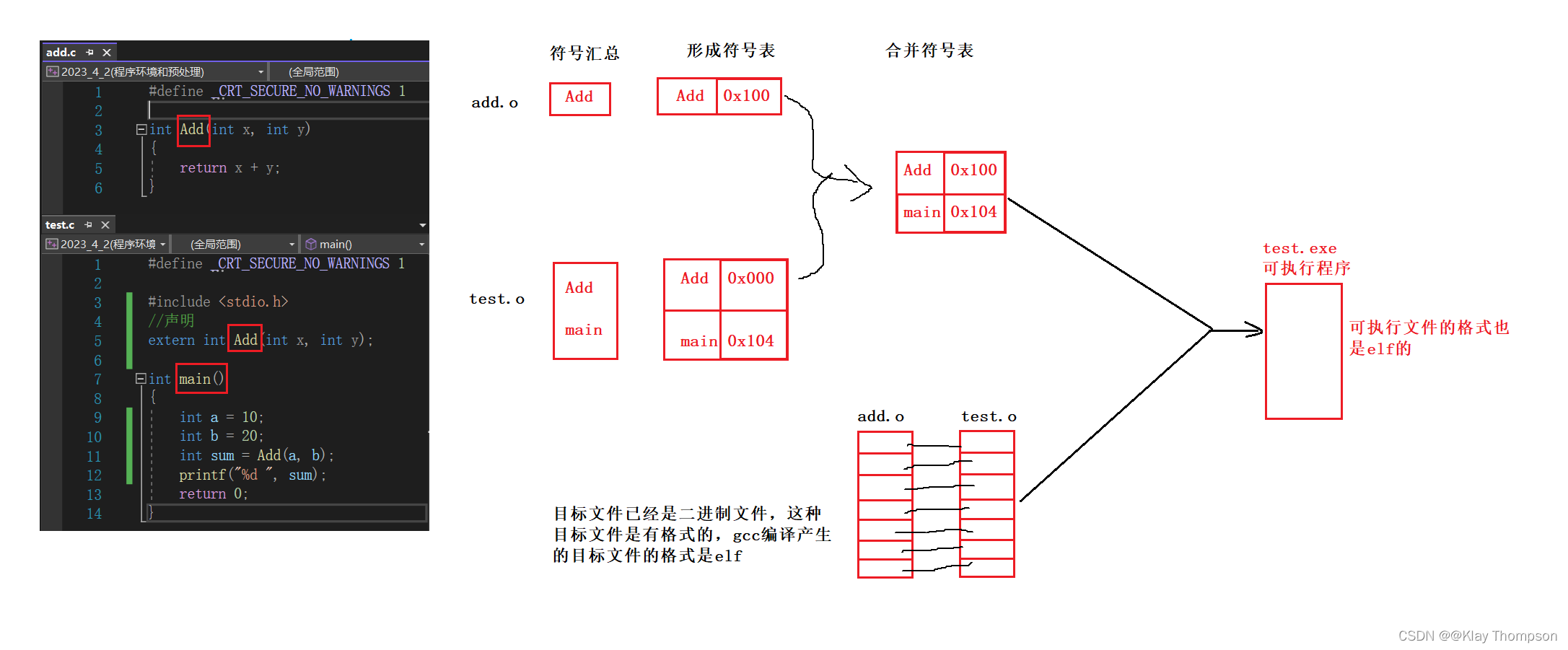
【程序环境详解】
每个源程序(.c文件)都需要经过编译链接形成 .exe的可执行文件。 在ANSI C的任何一种实现中,存在两个不同的环境 第一种是翻译环境,在这个环境中源代码被转换为可执行的机器指令。第二种是执行环境,它用于实际执行代码…...
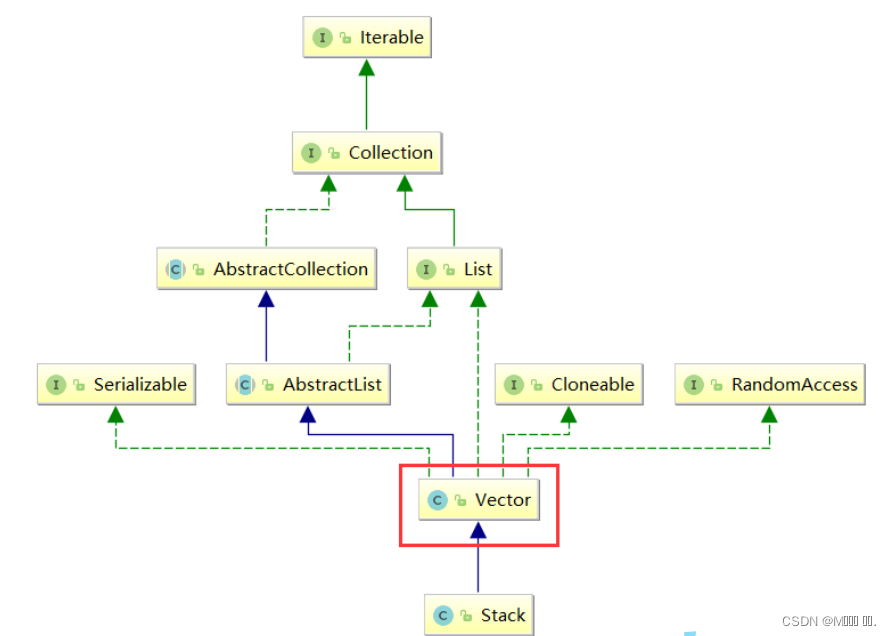
栈(Stack)
目录 1.1 概念 1.2 栈的使用 1.3 栈的模拟实现 1.4 栈的应用场景 1. 改变元素的序列 2. 将递归转化为循环 1.1 概念 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为…...
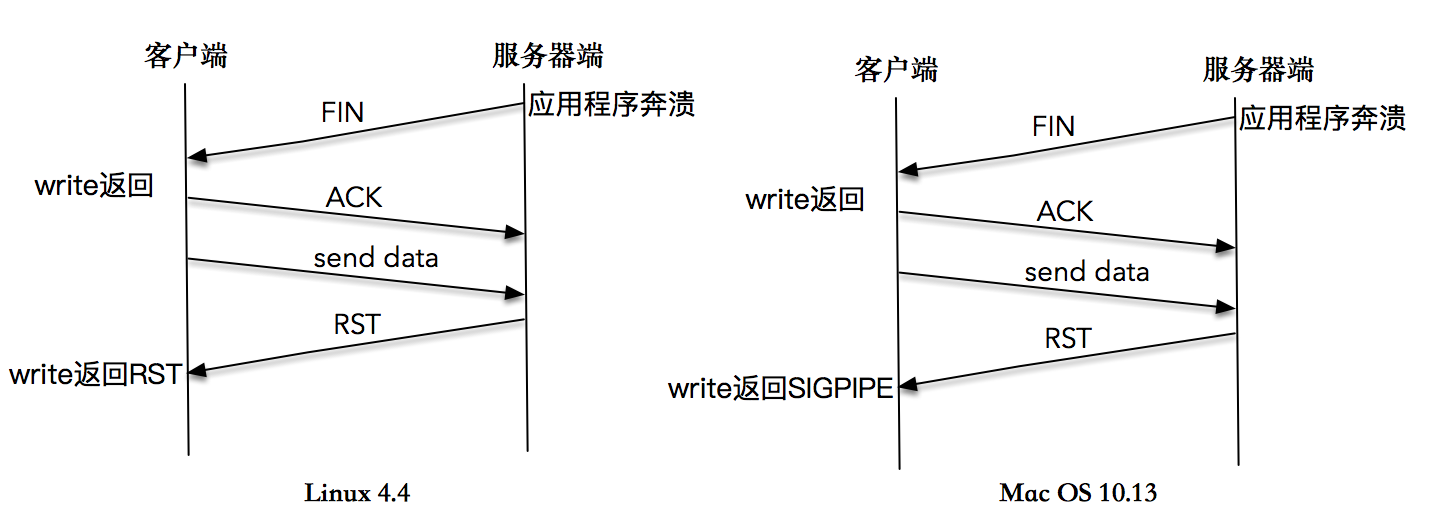
【计算机网络】2、网络编程模型理论
文章目录一、网络基本概念1.1 网段1.2 子网掩码 netmask1.3 子网 subnet1.4 网络地址 network1.5 实战 192.168.0.1/27 的含义二、socket2.1 sockaddr 格式2.1.1 IPv4 sockaddr 格式2.1.2 IPv6 sockaddr 格式2.1.3 本地 sockaddr 格式2.2 http 与 websocket三、TCP 编程3.1 ser…...

jmeter接口测试及详细步骤以及项目实战教程
如果看完这篇文章还是不太明白的话,可以看看下面这个视频 2023年B站最新Jmeter接口测试实战教程,精通接口自动化测试只需要这一套视频_哔哩哔哩_bilibili2023年B站最新Jmeter接口测试实战教程,精通接口自动化测试只需要这一套视频共计16条视…...

抖音进攻,B站退守
“爱优腾芒”等长视频平台的崛起,在一定层面上丰富了人们的日常生活,而抖音、快手等短视频平台的出现,则在很大程度上改变了用户观看视频的方式。只不过,近几年,随着流量增长逐渐遭遇瓶颈,各视频平台便纷纷…...
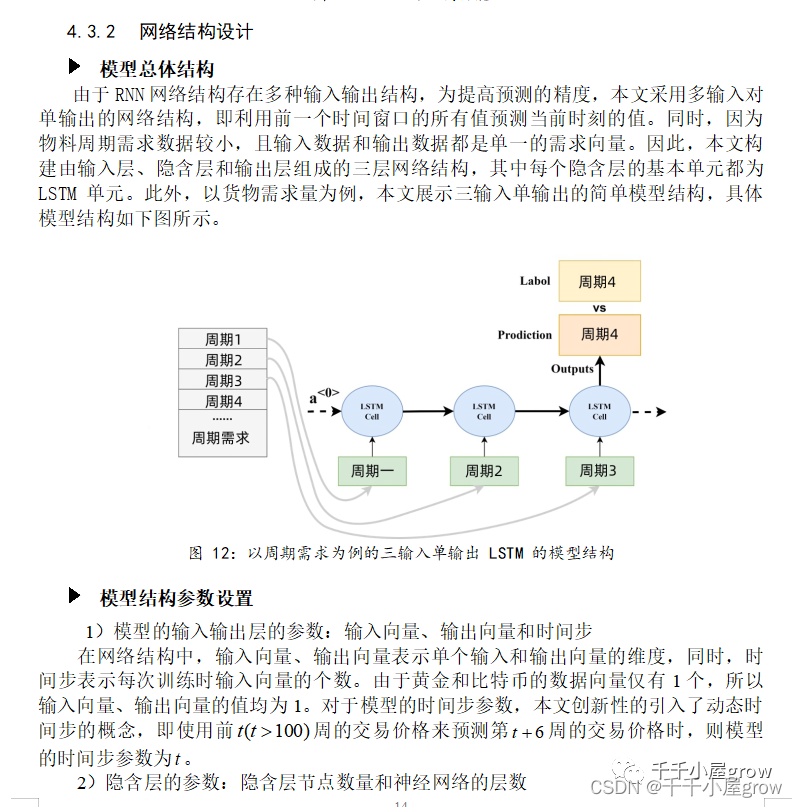
2022国赛E题完整成品文章数据代码模型--小批量物料的生产安排
基于LSTM循环神经网络的小批量物料生产安排分析 摘要 某电子产品制造企业面临以下问题:在多品种小批量的物料生产中,事先无法知道物料的 实际需求量。企业希望运用数学方法,分析已有的历史数据,建立数学模型,帮助企业…...
学生党,快来 Azure 一起学习 OpenAI (一):注册 Azure 和申请 OpenAI
大家好我是微软学生大使 Jambo , 在刚结束的微软学生开发者峰会 2023中我们了解到微软为学生提供了 Azure for Student 大礼包,通过 Azure for Student 除了学习和部署云原生的应用外,还可以申请使用 Microsoft OpenAI Service 。在这个 AIGC 火热的年代…...
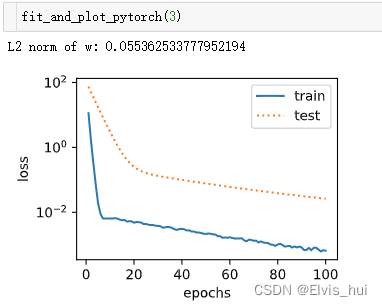
深入理解【正则化的L1-lasso回归和L2-岭回归】以及相关代码复现
正则化--L1-lasso回归和L2-岭回归1- 过拟合 欠拟合 模型选择2- 正则L1与L23- L2正则代码复现3-1 底层逻辑实现3-2 简洁实现1- 过拟合 欠拟合 模型选择 1-1 欠拟合: 在训练集和测试集上都不能很好的拟合数据【模型过于简单】 原因: 学习到的数据特征过少 …...
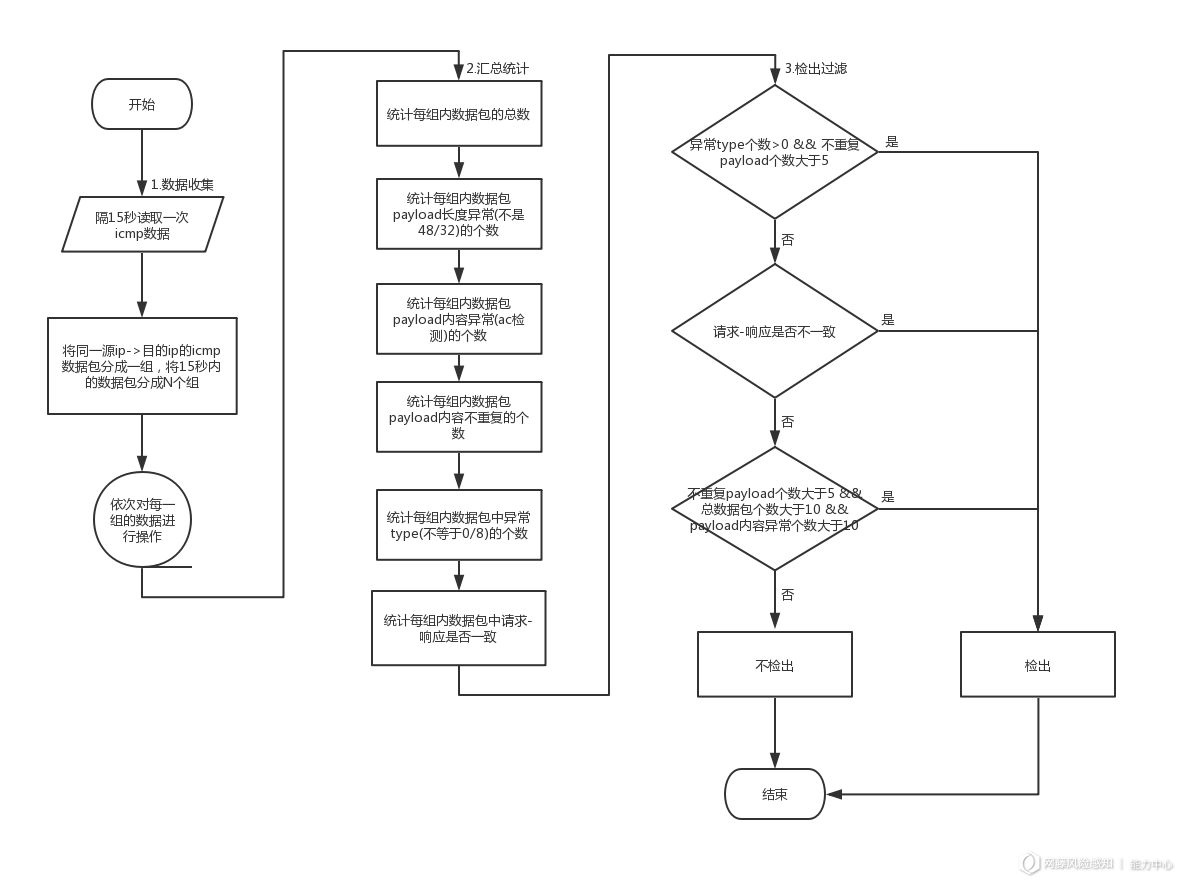
入侵检测——如何实现反弹shell检测?
反弹shell的本质:就是控制端监听在某TCP/UDP端口,被控端发起请求到该端口,并将其命令行的输入输出转到控制端。reverse shell与telnet,ssh等标准shell对应,本质上是网络概念的客户端与服务端的角色反转。 反弹shell的结…...
Python常用语句学习
人生苦短,我用Python。 ——吉多范罗苏姆 文章目录前言一、判断语句(一)if语句1. 作用2. 构成3. 语法4. 样例5.说明(二)if嵌套二、循环语句(一)while循环1. 作用2. 语法3. 样例4. 说明ÿ…...
测试3年还不如应届生,领导一句点醒:“公司不是只雇你来点点点的”
你的身边,是否有这样的景象? A:写了几年代码,写不下去了,听说测试很好上手,先来做几年测试 。 B:小文员一枚,想入行 IT,听说测试入门简单,请问怎么入行 。 …...

华为网络设备之路由策略,前缀列表(使用,规则)
华为网络之路由策略 前言:在企业网络的设备通信中,常面临一些非法流量访问的安全性及流量路径不优等问题,故为保证数据访问的安全性、提高链路带宽利用率,就需要对网络中的流量行为进行控制,如控制网络流量可达性、调…...

白噪音简介与实现
一、简介: 白噪音(White Noise)是一种具有平均功率频谱密度的噪音信号,其功率在所有频率上均匀分布。白噪音是一种随机信号,其包含所有频率成分的等幅随机振荡。因此,白噪音看起来像是一种随机的“嘈杂声”…...

Springboot结合线程池的使用
1.使用配置文件配置线程的参数 配置文件 thread-pool:core-size: 100max-size: 100keep-alive-seconds: 60queue-capacity: 1配置类 Component ConfigurationProperties("thread-pool") Data public class ThreadPoolConfig {private int coreSize;private int ma…...

AOP工作流程
AOP工作流程3,AOP工作流程3.1 AOP工作流程流程1:Spring容器启动流程2:读取所有切面配置中的切入点流程3:初始化bean流程4:获取bean执行方法验证容器中是否为代理对象验证思路步骤1:修改App类,获取类的类型步骤2:修改MyAdvice类,不增强步骤3:运行程序步骤…...
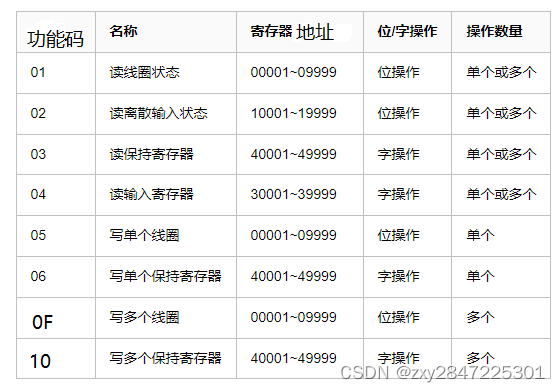
Modbus相关知识点及问题总结
本人水平有限,写得不对的地方望指正 困惑:线圈状态的值是否是存储在线圈寄存器里面?是否有线圈寄存器的说法?网上有说法说是寄存器占两个字节,但线圈的最少操作单位是位。类似于继电器的通断状态,直接根据电…...

【MySQL】函数
文章目录1. DQL执行顺序2. 函数2.1 字符串函数2.2 数值函数2.3 日期函数2.4 流程函数2.5 窗口函数2.5.1 介绍2.5.2 聚合窗口函数2.5.3 排名窗口函数2.5.4 取值窗口函数1. DQL执行顺序 2. 函数 2.1 字符串函数 函数功能concat(s1,s2,…sn)字符串拼接,将s1,s2…sn拼…...
MySQL高级
一、基础环境搭建 环境准备:CentOS7.6(系统内核要求是3.10以上的)、FinalShell 1. 安装Docker 帮助文档 : https://docs.docker.com/ 1、查看系统内核(系统内核要求是3.10以上的) uname -r2、如果之前安装过旧版本的D…...
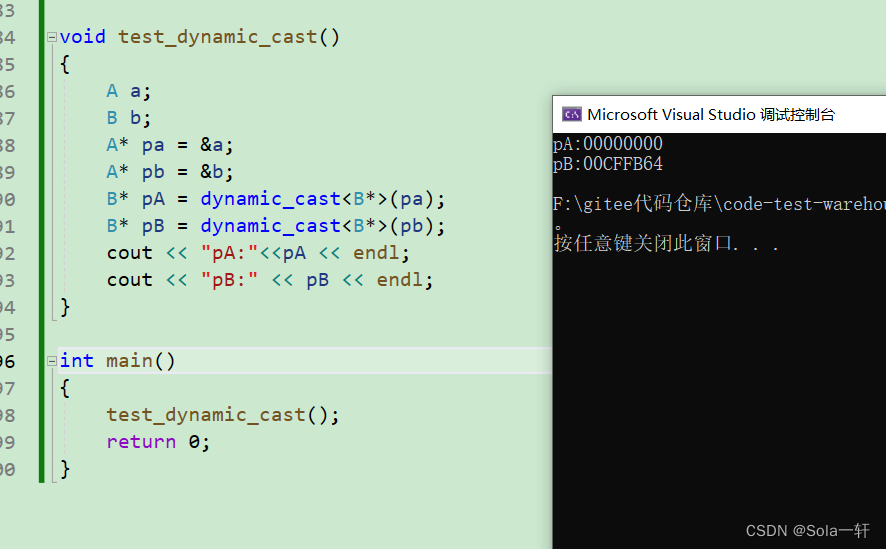
带你弄明白c++的4种类型转换
目录 C语言中的类型转换 C强制类型转换 static_cast reinterpret_cast const_cast dynamic_cast RTTI 常见面试题 这篇博客主要是帮助大家了解和学会使用C中规定的四种类型转换。首先我们先回顾一下C语言中的类型转换。 C语言中的类型转换 在C语言中,如果赋…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...
