深入理解【正则化的L1-lasso回归和L2-岭回归】以及相关代码复现
正则化--L1-lasso回归和L2-岭回归
- 1- 过拟合 欠拟合 模型选择
- 2- 正则L1与L2
- 3- L2正则代码复现
- 3-1 底层逻辑实现
- 3-2 简洁实现
1- 过拟合 欠拟合 模型选择
1-1 欠拟合:
-
在训练集和测试集上都不能很好的拟合数据【模型过于简单】
原因: 学习到的数据特征过少 -
解决办法:
1.得到更多的特征【特征组合,添加上下文特征,平台的特征】.
2.添加多项式特征,使得模型的泛化能力更强.
1-2 过拟合:
-
在训练集上表现很好,在测试集上表现不好【模型过于复杂】
-
问题: 特征存在异常,噪声,模型过于复杂
-
过拟合的一些解决办法
- 1.正则化:L1正则【使得特征系数为0 –Lasso回归】/L2正则【使得特征系数趋近于0–Ridge回归】
- 2.在神经网络里面:设置drop out 随机失活
- 3.提前终止训练 early stopping【正则化迭代学习方法,在验证错误率达到最小值的时候停止训练,通过限制错误率的阈值,进行停止】
- 4.随机森林里面:预剪枝和后剪枝
- 5.增加数据量【重采样】,清洗数据
- 6.减少特征维度,防止维度灾难
- 7.降低模型的复杂度,采用交叉验证等.
1-3 模型选择
- 模型选择是指如何选择最适合数据的模型。在选择模型时,需要考虑模型的复杂度、泛化能力、可解释性、训练时间和计算资源等因素。
常用的模型选择方法包括交叉验证、网格搜索、贝叶斯优化等。
- 交叉验证可以评估不同模型的性能
- 网格搜索可以在参数空间中搜索最优参数
- 贝叶斯优化则可以更有效地搜索参数空间
2- 正则L1与L2
为了防止过拟合,通常在线性的模型的基础上引入一个正则化项。$L_1$和$L_2$正则化中,正则项是模型参数的$L_1$范数和$L_2$范数。
- L1L_1L1: minw∑i=1m(yi−wTxi)2+λ∣∣w∣∣1\underset {w}{min}\sum^m_{i=1}(y_i-w^Tx_i)^2+\lambda||w||_1wmin∑i=1m(yi−wTxi)2+λ∣∣w∣∣1,当λ>0,就是Lasso回归,λ=0就是线性回归
- L2L_2L2: minw∑i=1m(yi−wTxi)2+λ∣∣w∣∣22\underset {w}{min}\sum^m_{i=1}(y_i-w^Tx_i)^2+\lambda||w||_2^2wmin∑i=1m(yi−wTxi)2+λ∣∣w∣∣22,当λ>0,就是岭回归,一般写成minw∑i=1m(yi−wTxi)2+λ2n∑w2\underset {w}{min}\sum^m_{i=1}(y_i-w^Tx_i)^2+\frac{\lambda}{2n}\sum w^2wmin∑i=1m(yi−wTxi)2+2nλ∑w2
Lasso回归中的L1正则项是绝对值之和,使得某些特征系数为0,岭回归中的L2正则项是平方和,使得某些特征系数趋近于0
#弹性网络 Elastic Net 综合lasso和ridge两个方法
from sklearn.linear_model import Ridge, ElasticNet, Lasso
Lasso回归和岭回归都是基于最小二乘法(OLS)的基础上进行的。OLS是通过最小化实际值和预测值之间的误差平方和来得到模型参数的,但是它容易产生过拟合的问题。为了解决这个问题,Lasso回归和岭回归引入了正则化项,对模型参数进行限制。
Lasso回归(Least Absolute Shrinkage and Selection Operator Regression)
- 通过在目标函数中加入L1正则项,将模型参数向零稀疏化。L1正则化在优化过程中会将一些不重要的特征对应的参数收缩到零,从而实现了特征选择的功能。Lasso回归可以在高维数据中寻找到较少的重要特征,从而提高了模型的泛化能力。
岭回归(Ridge Regression)
- 通过在目标函数中加入L2正则项,将模型参数平滑化。L2正则化在优化过程中会让所有参数都往零收缩,但是不会将任何参数完全收缩到零,从而保留了所有的特征,避免了Lasso回归可能出现的特征丢失问题。岭回归在处理多重共线性问题时效果很好,可以有效减少共线性带来的影响。
总之,Lasso回归和岭回归都是非常有用的正则化方法,可以在机器学习任务中提高模型的性能和稳定性。当数据集具有大量特征、多重共线性或者存在噪声时,这两种方法都可以用来提高模型的泛化能力和减少过拟合的风险
3- L2正则代码复现
3-1 底层逻辑实现
创建一个高维线性回归实验
y=0.05+∑i=1p0.01xi+εy=0.05+\sum^p_{i=1}0.01x_i+εy=0.05+∑i=1p0.01xi+ε,ε服从均值为0,标准差为0.01的正态分布
特征维度为200,将训练数据集的样本设低20
import numpy as np
import torch
import torch.nn as nn
#
n_train,n_test,num_inputs = 20,100,200#样本,特征
true_w,true_b = torch.ones(num_inputs,1)*0.01,0.05#生成特征
features =torch.randn((n_train+n_test,num_inputs))
labels = torch.matmul(features,true_w)+true_b
labels += torch.tensor(np.random.normal(0,0.01,size=labels.size()),dtype=torch.float)
#划分训练集和测试及
train_features, test_features = features[:n_train, :], features[n_train:, :]
train_labels, test_labels = labels[:n_train], labels[n_train:]
模型相关函数
#画图
def use_svg_display():# 用矢量图显示display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):use_svg_display()# 设置图的尺寸plt.rcParams['figure.figsize'] = figsize
def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None,legend=None, figsize=(3.5, 2.5)):set_figsize(figsize)plt.xlabel(x_label)plt.ylabel(y_label)plt.semilogy(x_vals, y_vals)if x2_vals and y2_vals:plt.semilogy(x2_vals, y2_vals, linestyle=':')plt.legend(legend)
def init_params():w = torch.randn((num_inputs,1),requires_grad = True)b = torch.zeros(1,requires_grad=True)return [w,b]
#定义L2范数,惩罚项
def l2_penalty(w):return (w**2).sum()/2
#定义模型
def linreg(X, w, b): return torch.mm(X, w) + b
#定义代价
def squared_loss(y_hat, y):# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2return (y_hat - y.view(y_hat.size())) ** 2 / 2
#定义随机梯度下降
def sgd(params, lr, batch_size): # for param in params:param.data -= lr * param.grad / batch_size#封装数据
dataset = torch.utils.data.TensorDataset(train_features,train_labels)
train_iter = torch.utils.data.DataLoader(dataset,batch_size,shuffle=True)
训练
batch_size,num_epochs,lr = 1,100,0.003#批次,迭代次数,学习率
#模型与损失均方误差函数
net=linreg
loss=squared_loss
#
def fit_and_plot(lambd):w,b=init_params()train_ls,test_ls=[],[]for _ in range(num_epochs):for X,y in train_iter:l = loss(net(X,w,b),y)+lambd*l2_penalty(w)l = l.sum()if w.grad is not None:#梯度清0w.grad.data.zero_()n.grad.data.zero_()l.backward()#反向传播sgd([w,b],lr,batch_size)#参数更新train_ls.append(loss(net(train_features,w,b),train_labels).mean().item())test_ls.append(loss(net(test_features,w,b),test_labels).mean().item())semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',range(1, num_epochs + 1), test_ls, ['train', 'test'])print('weight:', net.weight.data,'\nbias:', net.bias.data)
观察过拟合λ=0的情况
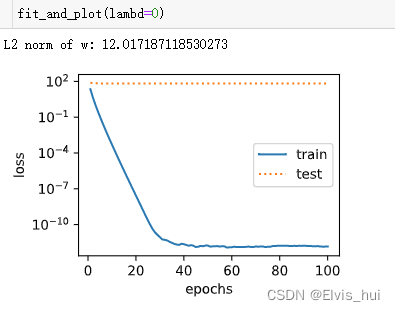
使用L2,λ>0
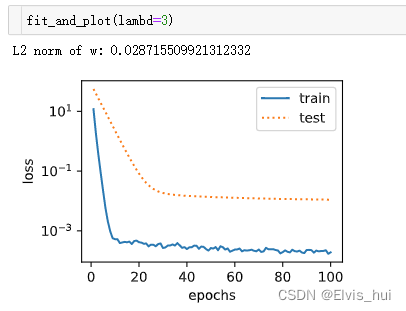
3-2 简洁实现
num_inputs = 200
def fit_and_plot_pytorch(wd):#对权重参数衰减,权重名称一般是以weight结尾net = nn.Linear(num_inputs ,1)nn.init.normal_(net.weight,mean=0,std=1)nn.init.normal_(net.bias,mean=0,std=1)optimizer_w = torch.optim.SGD(params = [net.weight],lr=lr,weight_decay=wd)#weight_decay权重衰减optimizer_b = torch.optim.SGD(params=[net.bias],lr=lr)#不对偏置进行衰减train_ls,test_ls = [],[]for _ in range(num_epochs):for X,y in train_iter:l = loss(net(X),y).mean()optimizer_w.zero_grad()optimizer_b.zero_grad()l.backward()#更新权重参数optimizer_w.step()optimizer_b.step()train_ls.append(loss(net(train_features),train_labels).mean().item())test_ls.append(loss(net(test_features),test_labels).mean().item())semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',range(1, num_epochs + 1), test_ls, ['train', 'test'])print('L2 norm of w:', net.weight.data.norm().item())
wd=0
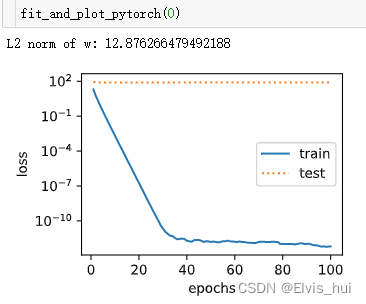
wd>0
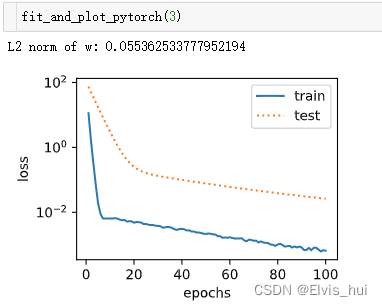
相关文章:

深入理解【正则化的L1-lasso回归和L2-岭回归】以及相关代码复现
正则化--L1-lasso回归和L2-岭回归1- 过拟合 欠拟合 模型选择2- 正则L1与L23- L2正则代码复现3-1 底层逻辑实现3-2 简洁实现1- 过拟合 欠拟合 模型选择 1-1 欠拟合: 在训练集和测试集上都不能很好的拟合数据【模型过于简单】 原因: 学习到的数据特征过少 …...
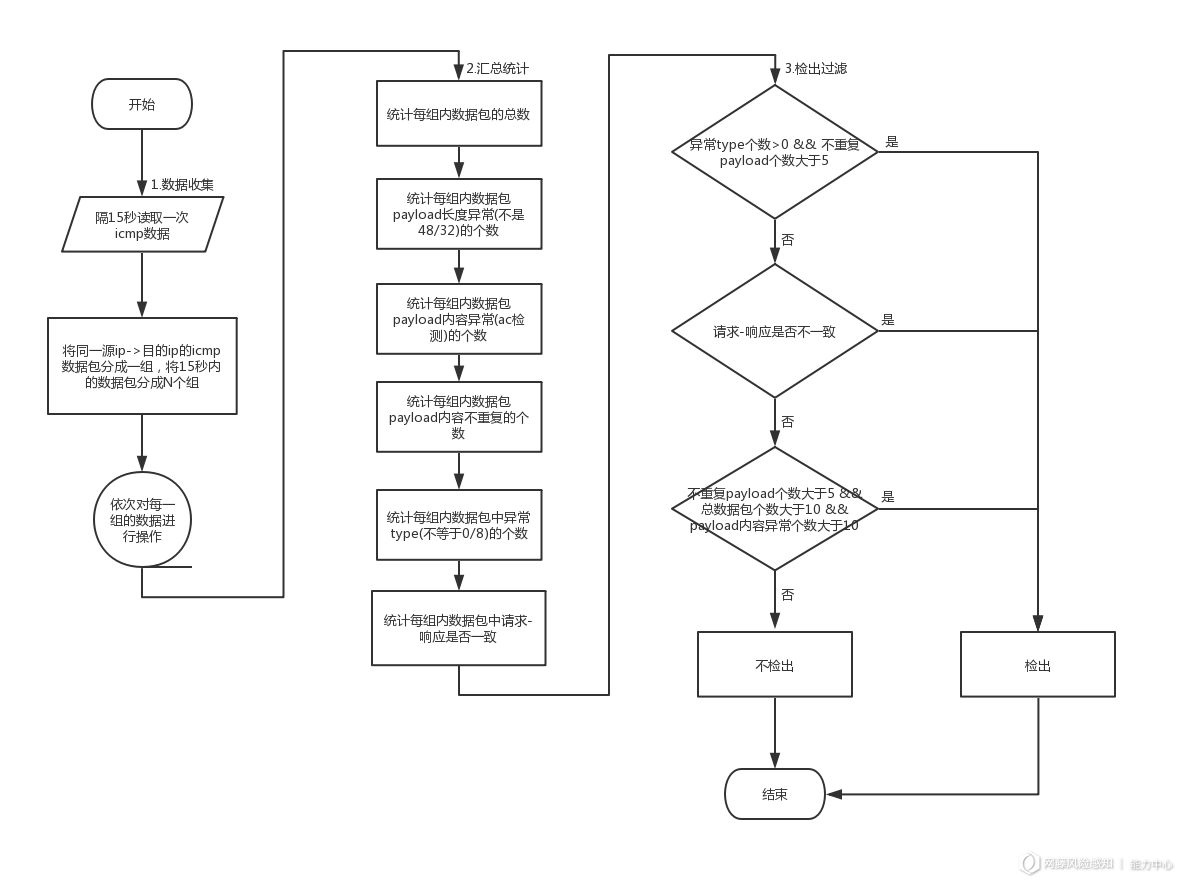
入侵检测——如何实现反弹shell检测?
反弹shell的本质:就是控制端监听在某TCP/UDP端口,被控端发起请求到该端口,并将其命令行的输入输出转到控制端。reverse shell与telnet,ssh等标准shell对应,本质上是网络概念的客户端与服务端的角色反转。 反弹shell的结…...
Python常用语句学习
人生苦短,我用Python。 ——吉多范罗苏姆 文章目录前言一、判断语句(一)if语句1. 作用2. 构成3. 语法4. 样例5.说明(二)if嵌套二、循环语句(一)while循环1. 作用2. 语法3. 样例4. 说明ÿ…...
测试3年还不如应届生,领导一句点醒:“公司不是只雇你来点点点的”
你的身边,是否有这样的景象? A:写了几年代码,写不下去了,听说测试很好上手,先来做几年测试 。 B:小文员一枚,想入行 IT,听说测试入门简单,请问怎么入行 。 …...

华为网络设备之路由策略,前缀列表(使用,规则)
华为网络之路由策略 前言:在企业网络的设备通信中,常面临一些非法流量访问的安全性及流量路径不优等问题,故为保证数据访问的安全性、提高链路带宽利用率,就需要对网络中的流量行为进行控制,如控制网络流量可达性、调…...

白噪音简介与实现
一、简介: 白噪音(White Noise)是一种具有平均功率频谱密度的噪音信号,其功率在所有频率上均匀分布。白噪音是一种随机信号,其包含所有频率成分的等幅随机振荡。因此,白噪音看起来像是一种随机的“嘈杂声”…...

Springboot结合线程池的使用
1.使用配置文件配置线程的参数 配置文件 thread-pool:core-size: 100max-size: 100keep-alive-seconds: 60queue-capacity: 1配置类 Component ConfigurationProperties("thread-pool") Data public class ThreadPoolConfig {private int coreSize;private int ma…...

AOP工作流程
AOP工作流程3,AOP工作流程3.1 AOP工作流程流程1:Spring容器启动流程2:读取所有切面配置中的切入点流程3:初始化bean流程4:获取bean执行方法验证容器中是否为代理对象验证思路步骤1:修改App类,获取类的类型步骤2:修改MyAdvice类,不增强步骤3:运行程序步骤…...
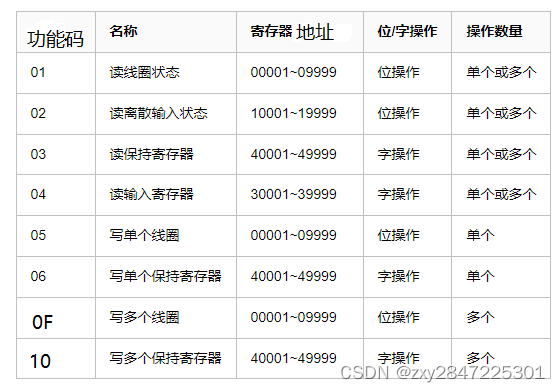
Modbus相关知识点及问题总结
本人水平有限,写得不对的地方望指正 困惑:线圈状态的值是否是存储在线圈寄存器里面?是否有线圈寄存器的说法?网上有说法说是寄存器占两个字节,但线圈的最少操作单位是位。类似于继电器的通断状态,直接根据电…...

【MySQL】函数
文章目录1. DQL执行顺序2. 函数2.1 字符串函数2.2 数值函数2.3 日期函数2.4 流程函数2.5 窗口函数2.5.1 介绍2.5.2 聚合窗口函数2.5.3 排名窗口函数2.5.4 取值窗口函数1. DQL执行顺序 2. 函数 2.1 字符串函数 函数功能concat(s1,s2,…sn)字符串拼接,将s1,s2…sn拼…...
MySQL高级
一、基础环境搭建 环境准备:CentOS7.6(系统内核要求是3.10以上的)、FinalShell 1. 安装Docker 帮助文档 : https://docs.docker.com/ 1、查看系统内核(系统内核要求是3.10以上的) uname -r2、如果之前安装过旧版本的D…...
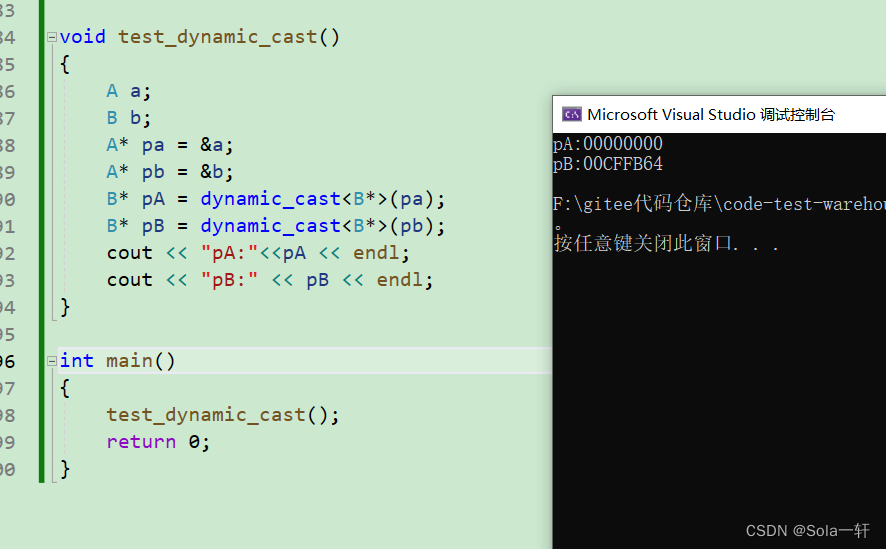
带你弄明白c++的4种类型转换
目录 C语言中的类型转换 C强制类型转换 static_cast reinterpret_cast const_cast dynamic_cast RTTI 常见面试题 这篇博客主要是帮助大家了解和学会使用C中规定的四种类型转换。首先我们先回顾一下C语言中的类型转换。 C语言中的类型转换 在C语言中,如果赋…...
8个明显可以提升数据处理效率的 Python 神库
在进行数据科学时,可能会浪费大量时间编码并等待计算机运行某些东西。所以我选择了一些 Python 库,可以帮助你节省宝贵的时间 文章目录1、Optuna技术提升2、ITMO\_FS3、Shap-hypetune4、PyCaret5、floWeaver6、Gradio7、Terality8、Torch-Handle1、Optun…...

互联网公司吐槽养不起程序员,IT岗位的工资真是虚高有泡沫了?
说实话,看到这个话题的时候又被震惊到。 因为相比以往,程序员工资近年来已经够被压缩的了好嘛? 那些鼓吹泡沫论的,真就“何不食肉糜”了~~~ 而且这种逻辑就很奇怪, 程序员的薪资难道不是由行业水平决定么ÿ…...
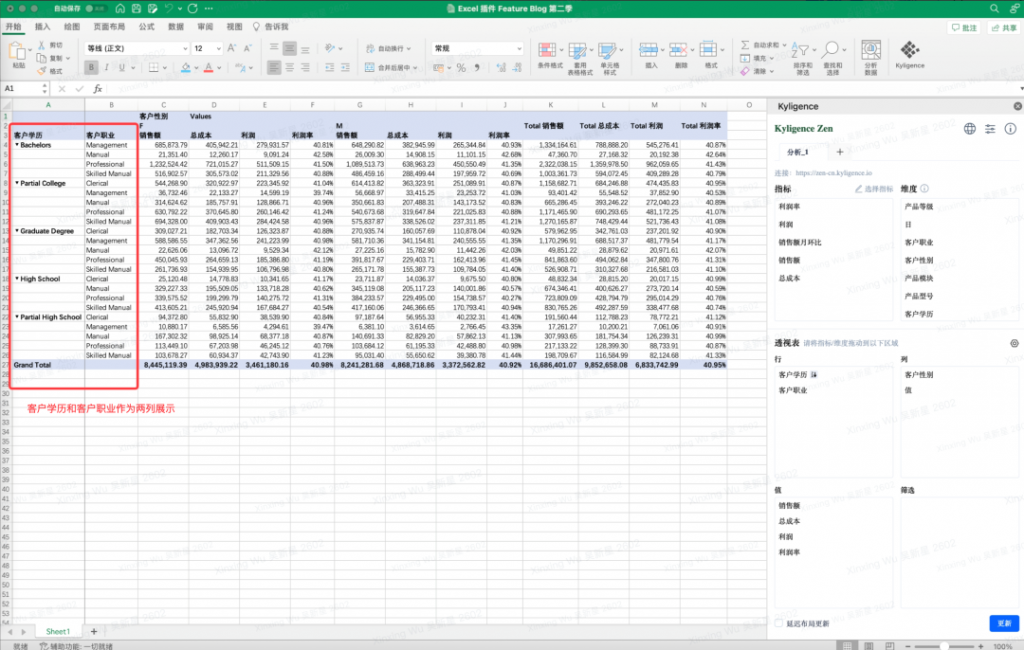
Excel 进阶|只会 Excel 也能轻松搭建指标应用啦
现在,Kyligence Zen 用户可在 Excel 中对指标进行更进一步的探索和分析,能够实现对维度进行标签筛选、对维度基于指标值进行筛选和排序、下钻/上卷、多样化的透视表布局、本地 Excel 和云端 Excel 的双向支持等。业务人员和分析师基于现有分析习惯就可以…...
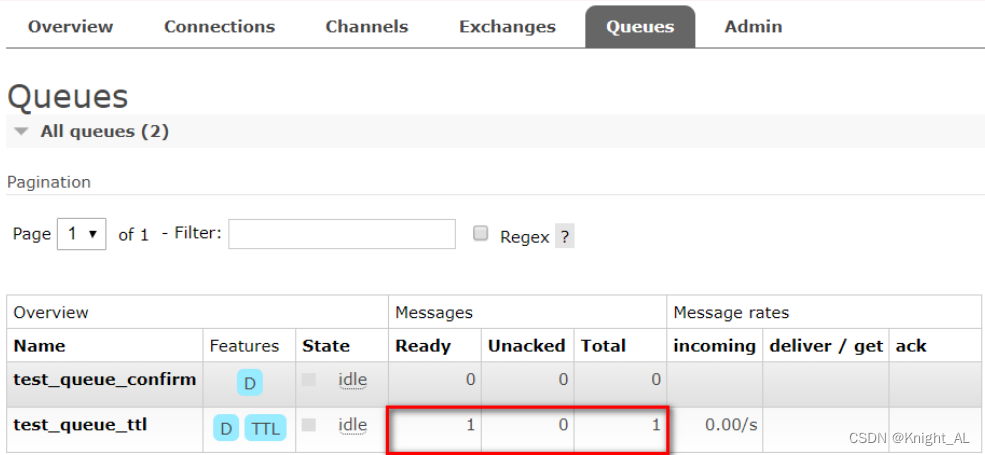
RabbitMQ中TTL
目录一、TTL1.控制后台演示消息过期2.代码实现2.1 队列统一过期2.2 消息过期一、TTL TTL 全称 Time To Live(存活时间/过期时间)。 当消息到达存活时间后,还没有被消费,会被自动清除。 RabbitMQ可以对消息设置过期时间࿰…...
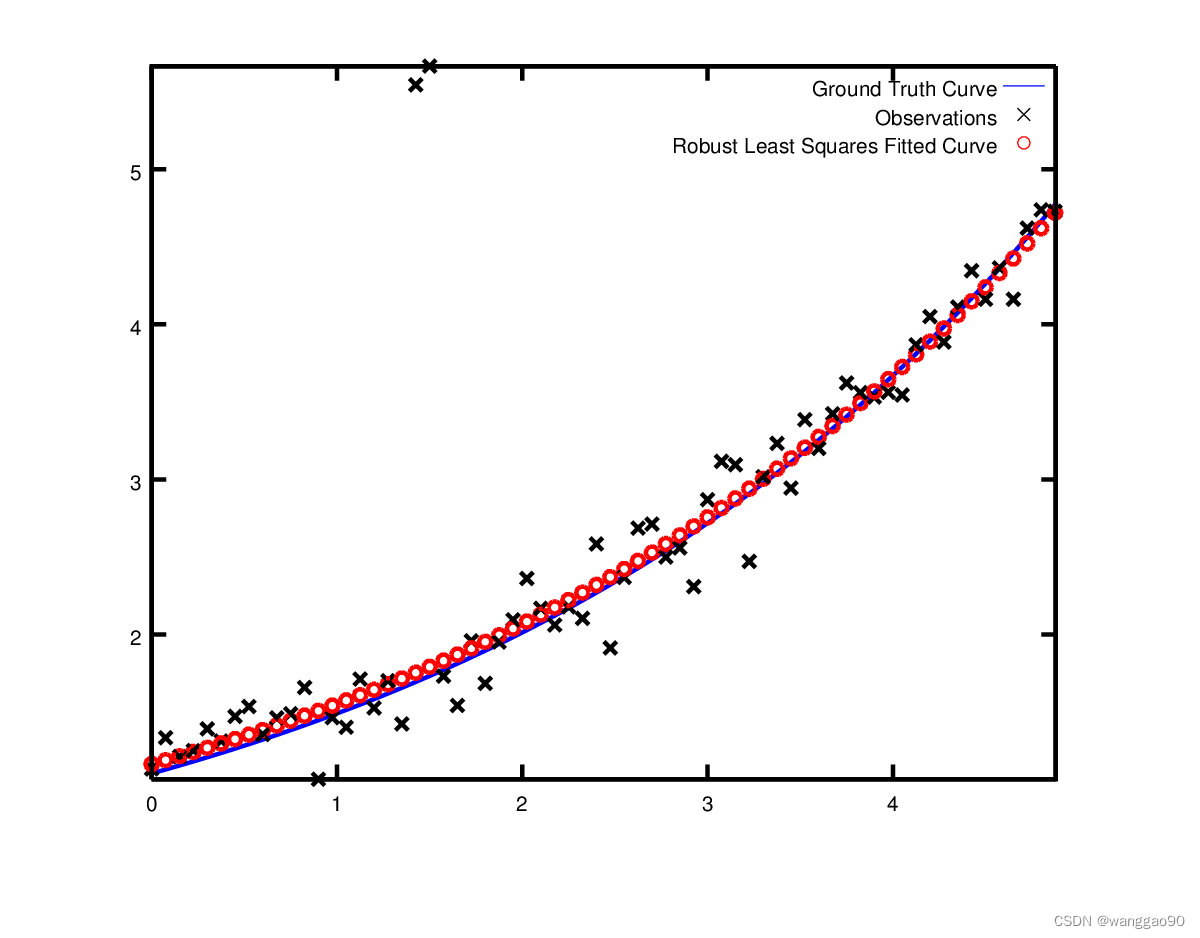
Ceres简介及示例(4)Curve Fitting(曲线拟合)
文章目录1、Curve Fitting1.1、残差定义1.2、 Problem问题构造1.3、完整代码1.4、运行结果2、Robust Curve Fitting1、Curve Fitting 到目前为止,我们看到的示例都是没有数据的简单优化问题。最小二乘和非线性最小二乘分析的原始目的是对数据进行曲线拟合。 以一个…...

音质最好的骨传导蓝牙耳机有哪些,推荐几款不错的骨传导耳机
骨传导耳机也称为“不入耳式”耳机,是一种通过颅骨、骨迷路、内耳淋巴液和听神经之间的信号传导,来达到听力保护目的的一种技术。由于它可以开放双耳,所以在跑步、骑行等运动时使用十分安全,可以避免外界的干扰。这种耳机在佩戴…...

计算机操作系统安全
操作系统安全是计算机系统安全的重要组成部分,目的是保护操作系统的机密性、完整性和可用性。在当前的网络环境下,操作系统面临着许多威胁,如病毒、木马、蠕虫、黑客攻击等等。为了保护操作系统的安全,需要采取各种措施来防范这些…...
超详细从入门到精通,pytest自动化测试框架实战教程-用例标记/执行(三)
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 pytest可以通过标记…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
