如何理解矩阵的复数特征值和特征向量?
实数特征值的直观含义非常好理解,它就是在对应的特征向量方向上的纯拉伸/压缩。
而复数特征值,我们可以把它放在复数域中理解。但是这里给出一个不那么简洁、但是更加直观的理解方式:把它放在实空间中。那么复数特征值表现的就是旋转+等比放大/缩小。我们不妨从一个二维空间说起:
对二维空间的一个线性变换:
A=(a11a12a12a22)
假设它有两个复数特征值:
λ=a±bi=r(cosθ±isinθ)
以及相对应的两个特征向量:
v=(x1x2)±i(y1y2)
也就是说,虽然每个特征值都有一个实部和一个虚部(两个自由度),但是由于特征值必然是共轭成对出现的,那么两个特征值仍然只对应着一个实部和一个虚部(两个自由度)。对特征向量而言同理。
也就是说,一对复特征值给我们两个自由度,一个模,一个幅角。一对特征向量也给我们两个向量,一个是实部向量,一个是虚部向量。
于是乎,如下两个向量:
,(x1x2), (y1y2)
就可以构成一个二维空间的一组基。
那么可以证明,当我们选取这两个向量为基时,原线性变换的表述就变成了:
B=r(cos(θ)−sin(θ)sin(θ)cos(θ))
这是一个旋转矩阵乘以一个数字。也就是说,在特征向量的实部和虚部构成的基底下,这个线性变换就是一个纯粹的旋转 θ 外加一个等比放大倍数 r 。
比如说,我们令(简化起见,选取行列式为1的矩阵)
A=(0.7−0.50.61)
这个矩阵把下图中蓝色的空间变换成红色的空间:

我们可以按照上述的原则进行坐标变换,变换的结果就是这样的:

我们可以看到,经过坐标变换后,蓝色空间变为红色空间就是一个纯粹的旋转过程了。这里,复数特征值和特征向量的含义就是:
- 特征值的模代表着等比放大的倍数
- 特征值的幅角代表着旋转的角度
- 特征向量的实部向量和虚部向量代表着实现上述变换的一组基
我们可以很容易推广到三维空间的变换,对一个三维矩阵:
A=(a11a12a13a21a22a23a31a32a33)
我们假设这个矩阵有三个不重叠的特征值,其中两个为共轭复数:
λ1/2=a±bi,λ3=c
那么,可以证明这个矩阵和下面这样一个分块矩阵相似,也就是说,我们可以通过选取某一个坐标系,把这个线性变换写成如下形式:
B=(ab0−ba000c)
我们令:
r=a2+b2, a=rcos(θ), b=rsin(θ)
那么,可以看到:
B=(cos(θ)−sin(θ)0sin(θ)cos(θ)0001)(r000r000c)
我们可以看到,这个变换就可以被分解成两个单独的变换,一个是纯旋转:在x-y平面中的旋转,另一个纯伸缩:在x-y平面上的均匀拉伸r倍,以及在z方向上单向拉伸c倍。
实现这种变换的基就是复特征向量的实部向量、虚部向量、以及实特征值的特征向量。具体讲,假定矩阵A的特征向量为:
v1/2=(x1x2x3)±i(y1y2y3), v3=(z1z2z3)
那么,这三个基底就是:
(x1x2x3), (y1y2y3), (z1z2z3)
也就是说,当我们拿到任意一个三维矩阵(注意,这里不考虑特征值重根的情况):
- 我们可以把这个矩阵变成一个纯旋转和一个纯伸缩的两个变换的组合。
- 纯旋转的角度就是复数特征值的幅角,旋转发生在复特征向量的实部向量和虚部向量所构成的平面中。
- 纯伸缩的倍数在各个方向上分别是复特征向量的模、以及实特征向量本身。
如果我们继续推广到高维空间,一个线形变换可以通过上述基底的选择表示成:
{(cosθ1−sinθ1sinθ1cosθ1)0⋯001⋯0⋮⋮⋱⋮00⋯(cosθi−sinθisinθicosθi)}{r100⋯000r10⋯0000λ3⋯00⋮⋮⋮⋱⋮⋮00⋯ri000⋯0ri}
也是纯旋转+纯伸缩的两种变换的组合。
相关文章:

如何理解矩阵的复数特征值和特征向量?
实数特征值的直观含义非常好理解,它就是在对应的特征向量方向上的纯拉伸/压缩。 而复数特征值,我们可以把它放在复数域中理解。但是这里给出一个不那么简洁、但是更加直观的理解方式:把它放在实空间中。那么复数特征值表现的就是旋转等比放大…...

怎么查看网站是否被谷歌收录,查看网站是否被搜索引擎收录5个方法与步骤
要查看网站是否被谷歌(Google)或其他搜索引擎收录,是网站管理和SEO(搜索引擎优化)中的一个重要环节。以下是查看网站是否被搜索引擎收录5个方法与步骤,帮助您确认网站是否被搜索引擎成功索引: …...

Java工具--stream流
Java工具--stream流 过滤(filter)统计求最大最小和均值求和(sum)过滤后,对数据进行统计 遍历(map)规约(reduce)排序(sorted)去重(dist…...
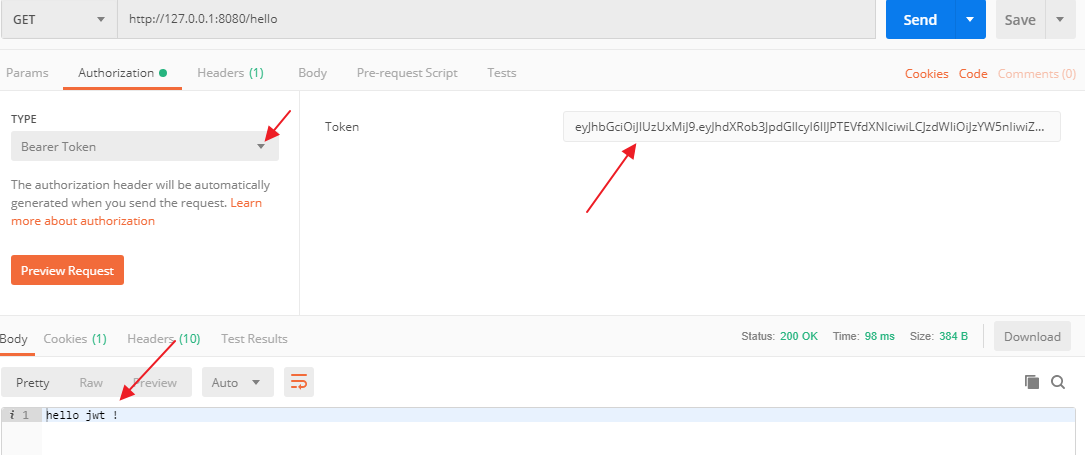
什么是 JWT?它是如何工作的?
松哥最近辅导了几个小伙伴秋招,有小伙伴在面小红书时遇到这个问题,这个问题想回答全面还是有些挑战,松哥结合之前的一篇旧文和大伙一起来聊聊。 一 无状态登录 1.1 什么是有状态 有状态服务,即服务端需要记录每次会话的客户端信…...

微信小程序使用picker,数组怎么设置默认值
默认先显示请选择XXX。然后点击弹出选择列表。如果默认value是0的话,他就直接默认显示数组的第一个了。<picker mode"selector" :value"planIndex" :range"planStatus" range-key"label" change"bindPlanChange&qu…...

Springboot生成树工具类,可通过 id/code 编码生成 2.0版本
优化工具类中,查询父级时便利多次的问题 import org.apache.commons.collections4.CollectionUtils; import org.apache.commons.lang3.mutable.MutableLong; import org.springframework.lang.NonNull; import org.springframework.lang.Nullable; import org.spri…...

17、CPU缓存架构详解高性能内存队列Disruptor实战
1.CPU缓存架构详解 1.1 CPU高速缓存概念 CPU缓存即高速缓冲存储器,是位于CPU与主内存间的一种容量较小但速度很高的存储器。CPU高速缓存可以分为一级缓存,二级缓存,部分高端CPU还具有三级缓存,每一级缓存中所储存的全部数据都是…...

算法训练营打卡Day18
目录 二叉搜索树的最小绝对差二叉搜索树中的众数二叉树的最近公共祖先额外练手题目 题目1、二叉搜索树的最小绝对差 力扣题目链接(opens new window) 给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。 示例: 思…...

【leetcode】169.多数元素
boyer-moore算法最简单理解方法: 假设你在投票选人 如果你和候选人(利益)相同,你就会给他投一票(count1),如果不同,你就会踩他一下(count-1)当候选人票数为0&…...

MyBatis<foreach>标签的用法与实践
foreach标签简介 实践 demo1 简单的一个批量更新,这里传入了一个List类型的集合作为参数,拼接到 in 的后面 ,来实现一个简单的批量更新 <update id"updateVislxble" parameterType"java.util.List">update model…...

R语言Shiny包新手教程
R语言Shiny包新手教程 1. 简介 Shiny 是一个 R 包,用于创建交互式网页应用。它非常适合展示数据分析结果和可视化效果。 2. 环境准备 安装R和RStudio 确保你的计算机上安装了 R 和 RStudio。你可以从 CRAN 下载 R,或从 RStudio 官网 下载 RStudio。…...

[大象快讯]:PostgreSQL 17 重磅发布!
家人们,数据库界的大新闻来了!📣 PostgreSQL 17 正式发布,全球开发者社区的心血结晶,带来了一系列令人兴奋的新特性和性能提升。 发版通告全文如下 PostgreSQL 全球开发小组今天(2024-09-26)宣布…...

CHI trans--Home节点发起的操作
总目录: CHI协议简读汇总-CSDN博客https://blog.csdn.net/zhangshangjie1/article/details/131877216 Home节点能够发起的操作,包含如下几类: Home to Subordinate Read transactionsHome to Subordinate Write transactionsHome to Subor…...

Rust和Go谁会更胜一筹
在国内,我认为Go语言会成为未来的主流,因为国内程序员号称码农,比较适合搬砖,而Rust对心智要求太高了,不适合搬砖。 就个人经验来看,Go语言简单,下限低,没有什么心智成本,…...

记HttpURLConnection下载图片
目录 一、示例代码1 二、示例代码2 一、示例代码1 import java.io.*; import java.net.HttpURLConnection; import java.net.URL;public class Test {/*** 下载图片*/public void getNetImg() {InputStream inStream null;FileOutputStream fOutStream null;try {// URL 统…...
物联网实训室建设的必要性
物联网实训室建设的必要性 一、物联网发展的背景 物联网(IoT)是指通过信息传感设备,按照约定的协议,将任何物品与互联网连接起来,进行信息交换和通信,以实现智能化识别、定位、跟踪、监控和管理的一种网络…...

初识C语言(四)
目录 前言 十一、常见关键字(补充) (1)register —寄存器 (2)typedef类型重命名 (3)static静态的 1、修饰局部变量 2、修饰全局变量 3、修饰函数 十二、#define定义常量和宏…...
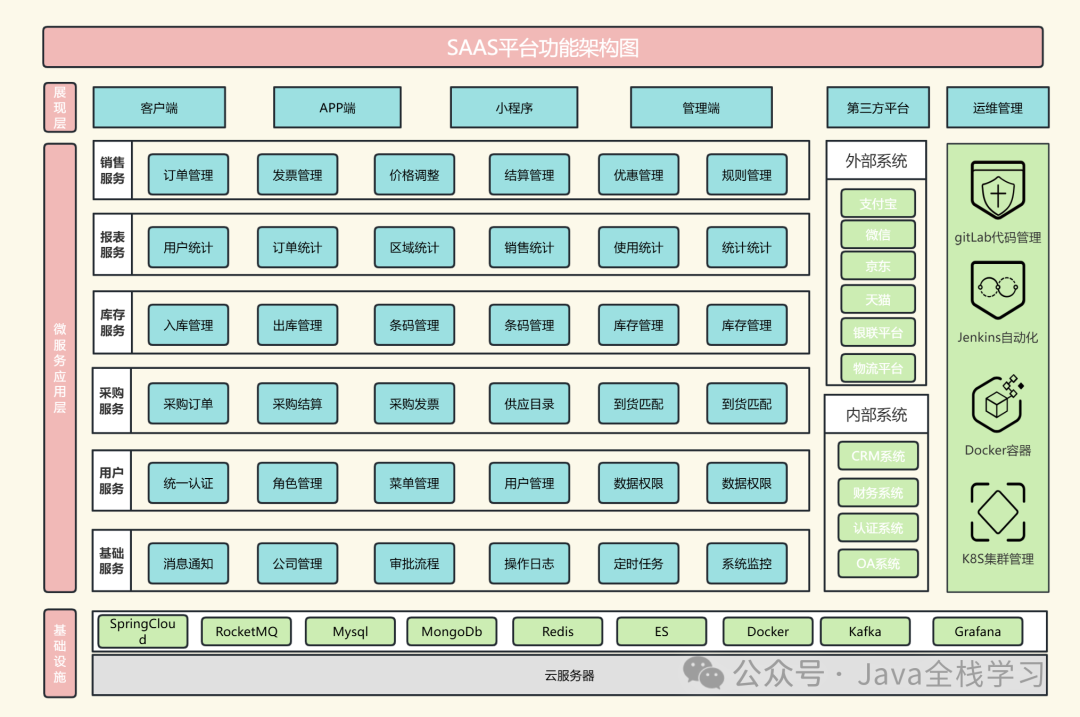
产品架构图:从概念到实践
在当今快速发展的科技时代,产品架构图已成为产品经理和设计师不可或缺的工具。它不仅帮助我们理解复杂的产品体系,还能指导我们进行有效的产品设计和开发。本文将深入探讨产品架构图的概念、重要性以及绘制方法。 整个内容框架分为三个部分,…...

smartctl 命令:查看硬盘健康状态
一、命令简介 smartctl 命令用于获取硬盘的 SMART 信息。 介绍硬盘SMART 硬盘的 SMART (Self-Monitoring, Analysis, and Reporting Technology) 技术用于监控硬盘的健康状态,并能提供一些潜在故障的预警信息。通过查看 SMART 数据,用户可以了解硬…...

BBR 为什么没有替代 CUBIC 成为 Linux 内核缺省算法
自 2017 年底 bbr 发布以来,随着媒体的宣讲,各大站点陆续部署 bbr,很多网友不禁问,bbr 这么好,为什么不替代 cubic 成为 linux 的缺省算法。仅仅因为它尚未标准化?这么好的算法又为什么没被标准化ÿ…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
