Leetcode.1665 完成所有任务的最少初始能量
题目链接
Leetcode.1665 完成所有任务的最少初始能量 Rating : 1901
题目描述
给你一个任务数组 tasks,其中 tasks[i] = [actuali, minimumi]:
actuali是完成第 i 个任务 需要耗费 的实际能量。minimumi是开始第 i 个任务前需要达到的最低能量。
比方说,如果任务为 ````[10, 12]```且你当前的能量为 11 ,那么你不能开始这个任务。如果你当前的能量为 13 ,你可以完成这个任务,且完成它后剩余能量为 3 。
你可以按照 任意顺序 完成任务。
请你返回完成所有任务的 最少 初始能量。
示例 1:
输入:tasks = [[1,2],[2,4],[4,8]]
输出:8
解释:
一开始有 8 能量,我们按照如下顺序完成任务:
- 完成第 3 个任务,剩余能量为 8 - 4 = 4 。
- 完成第 2 个任务,剩余能量为 4 - 2 = 2 。
- 完成第 1 个任务,剩余能量为 2 - 1 = 1 。
注意到尽管我们有能量剩余,但是如果一开始只有 7 能量是不能完成所有任务的,因为我们无法开始第 3 个任务。
示例 2:
输入:tasks = [[1,3],[2,4],[10,11],[10,12],[8,9]]
输出:32
解释:
一开始有 32 能量,我们按照如下顺序完成任务:
- 完成第 1 个任务,剩余能量为 32 - 1 = 31 。
- 完成第 2 个任务,剩余能量为 31 - 2 = 29 。
- 完成第 3 个任务,剩余能量为 29 - 10 = 19 。
- 完成第 4 个任务,剩余能量为 19 - 10 = 9 。
- 完成第 5 个任务,剩余能量为 9 - 8 = 1 。
示例 3:
输入:tasks = [[1,7],[2,8],[3,9],[4,10],[5,11],[6,12]]
输出:27
解释:
一开始有 27 能量,我们按照如下顺序完成任务:
- 完成第 5 个任务,剩余能量为 27 - 5 = 22 。
- 完成第 2 个任务,剩余能量为 22 - 2 = 20 。
- 完成第 3 个任务,剩余能量为 20 - 3 = 17 。
- 完成第 1 个任务,剩余能量为 17 - 1 = 16 。
- 完成第 4 个任务,剩余能量为 16 - 4 = 12 。
- 完成第 6 个任务,剩余能量为 12 - 6 = 6 。
提示:
- 1<=tasks.length<=1051 <= tasks.length <= 10^51<=tasks.length<=105
- 1<=actuali<=minimumi<=1041 <= actuali <= minimumi <= 10^41<=actuali<=minimumi<=104
解法:贪心 + 排序
我们假设 ppp 为能够完成所有任务的能量。有 (a0,m0),(a1,m1),(a2,m2),(a3,m3),....,(an−1,mn−1)(a_0,m_0),(a_1,m_1) ,(a_2,m_2),(a_3,m_3),....,(a_{n-1},m_{n-1})(a0,m0),(a1,m1),(a2,m2),(a3,m3),....,(an−1,mn−1),共 nnn 个任务。
按照题目的要求,如下不等式成立:
- p≥m0p \geq m_0p≥m0
- p−a0≥m1p - a_0 \geq m_1p−a0≥m1
- p−a0−a1≥m2p - a_0 - a_1 \geq m_2p−a0−a1≥m2
- p−a0−a1−a2≥m3p - a_0 - a_1 - a_2 \geq m_3p−a0−a1−a2≥m3
- …
- p−a0−a1−a2−a3−...−an−2≥mn−1p - a_0 - a_1 - a_2 - a_3 - ...-a_{n-2} \geq m_{n-1}p−a0−a1−a2−a3−...−an−2≥mn−1
将其整理一下,得:
- p≥m0p \geq m_0p≥m0
- p≥a0+m1p \geq a_0 + m_1p≥a0+m1
- p≥a0+a1+m2p \geq a_0 +a_1 + m_2p≥a0+a1+m2
- p≥a0+a1+a2+m3p \geq a_0 +a_1 + a_2 + m_3p≥a0+a1+a2+m3
- …
- p≥a0+a1+a2+a3+....+an−2+mn−1p \geq a_0 +a_1 + a_2 + a_3 + .... +a_{n-2} + m_{n-1}p≥a0+a1+a2+a3+....+an−2+mn−1
由于我们要求的是最少的能量,即我们要使 ppp 的最大值 最小化。
我们现在考虑,是否能让上面 n 个不等式右侧的最大值 变小。
我们可以尝试交换相连的两项,看看会发生什么。交换 (ai,mi)(a_i,m_i)(ai,mi) 和 (ai+1,mi+1)(a_{i+1},m_{i+1})(ai+1,mi+1)两项。
交换之前:
- p≥a0+a1+a2+a3+....+ai−1+mi=P(i)p \geq a_0 +a_1 + a_2 + a_3 + .... +a_{i-1} + m_i = P(i)p≥a0+a1+a2+a3+....+ai−1+mi=P(i)
- p≥a0+a1+a2+a3+....+ai−1+ai+mi+1=P(i+1)p \geq a_0 +a_1 + a_2 + a_3 + .... +a_{i-1} + a_i + m_{i+1} = P(i+1)p≥a0+a1+a2+a3+....+ai−1+ai+mi+1=P(i+1)
交换之后:
- p≥a0+a1+a2+a3+....+ai−1+mi+1=P′(i)p \geq a_0 +a_1 + a_2 + a_3 + .... +a_{i-1} + m_{i+1} = P'(i)p≥a0+a1+a2+a3+....+ai−1+mi+1=P′(i)
- p≥a0+a1+a2+a3+....+ai−1+ai+1+mi=P′(i+1)p \geq a_0 +a_1 + a_2 + a_3 + .... +a_{i-1} + a_{i+1} + m_i = P'(i+1)p≥a0+a1+a2+a3+....+ai−1+ai+1+mi=P′(i+1)
暂时只考虑这两项。交换之前的最大值为:max{P(i),P(i+1)}max\{P(i) , P(i+1)\}max{P(i),P(i+1)};交换之后的最大值为: max{P′(i),P′(i+1)}max\{P'(i) , P'(i+1)\}max{P′(i),P′(i+1)};
因为 P′(i+1)>P(i)P'(i+1) > P(i)P′(i+1)>P(i) , P(i+1)>P′(i)P(i+1) > P'(i)P(i+1)>P′(i)。
我们要想让交换之后的最大值变小,即 max{P′(i),P′(i+1)}<max{P(i),P(i+1)}max\{P'(i) , P'(i+1)\} < max\{P(i) , P(i+1)\}max{P′(i),P′(i+1)}<max{P(i),P(i+1)}。
等价于 P′(i+1)<P(i+1)P'(i+1) < P(i+1)P′(i+1)<P(i+1),即 a0+a1+a2+a3+....+ai−1+ai+1+mi<a0+a1+a2+a3+....+ai−1+ai+mi+1a_0 +a_1 + a_2 + a_3 + .... +a_{i-1} + a_{i+1} + m_i < a_0 +a_1 + a_2 + a_3 + .... +a_{i-1} + a_i + m_{i+1}a0+a1+a2+a3+....+ai−1+ai+1+mi<a0+a1+a2+a3+....+ai−1+ai+mi+1。
化简得,ai−mi>ai+1−mi+1a_i - m_i > a_{i+1} - m_{i+1}ai−mi>ai+1−mi+1。
所以我们要做的就是,找出所有的满足这样条件 ai−mi>ai+1−mi+1a_i - m_i > a_{i+1} - m_{i+1}ai−mi>ai+1−mi+1 的相连两项,并将它们交换位置。这样做不一定会让最大值减小,但是绝对不会让最大值增大。
实际上我们没必要去模拟这个过程。我们只需要让 tasks 按照 ai−mia_i - m_iai−mi从小到大的排序,最后再遍历模拟这个求最大值的过程即可。
时间复杂度:O(nlogn)O(nlogn)O(nlogn)
C++代码:
class Solution {
public:int minimumEffort(vector<vector<int>>& tasks) {sort(tasks.begin(),tasks.end(),[&](auto &a,auto &b){return a[0] - a[1] < b[0] - b[1];}) ;int p = 0 , s = 0;for(auto &e:tasks){p = max(p,s + e[1]);s += e[0];}return p;}
};相关文章:

Leetcode.1665 完成所有任务的最少初始能量
题目链接 Leetcode.1665 完成所有任务的最少初始能量 Rating : 1901 题目描述 给你一个任务数组 tasks,其中 tasks[i] [actuali, minimumi]: actuali是完成第 i 个任务 需要耗费 的实际能量。minimumi是开始第 i 个任务前需要达到的最低能…...
【C++笔试强训】第一天
选择题 解析:在for循环的循环条件(y 123) && (x < 4)中 ,&& 表示逻辑与,从左向右判断两边条件是否成立,只有当两边的条件都为真时,这条语句才为真。左边y 123是赋值语句,一直为真&…...

【网络安全软件】上海道宁与Cybereason为您提供未雨绸缪的攻击保护,终结对端点、整个企业以及网络上任何角落的网络攻击
Cybereason可收集 计算机网络内任何活动方面的数据 如运行当中的程序 被用户访问的文件以及 员工及任何获授权使用网络中的计算机人的 键盘输入和鼠标移动情况 Cybereason提供 即时结束网络攻击的精确度 在计算机、移动设备、服务器和云中 到战斗移动的任何地方 一、开…...

基于RK3568的Android11 适配 MIPI 屏幕
文章目录 前言一、mipi接口是什么?二、原理图三、屏幕点亮流程四、屏幕关键参数1.General Specification2. Power on/off sequence3.Timing五、屏幕初始化序列改写如何把原厂给的数据转换为设备需要的时序dcs小知识:初始化时序:退出时序:总结前言 在本小节会学习到如何适配…...

Ubuntu安装python
CentOS 安装 Python3 没什么坑,按照步骤一步步来就可以了。 但 Ubuntu 安装 Python3 的坑却不少,这里总结一下,避免以后继续踩坑。 我用的是 ubuntu16.04,安装最新版本的 Python3.8.3 第1步:安装编译环境 安装之前…...
)
django 运用pycharm的各种故障汇总(1)
一.用django入门第一个问题:pycharm的[community]社区版-免费开源与[professional]专业版注册收费两个版本:用django只能有[professional]版本便捷、专业; 解决方案的各种学习总结: 1.破解版:网上找了很多资料,基本已经没效果,不要报太大希望; 2.找中间途径然后有:Python 、…...

【设计模式】单例模式Singleton(Java)
文章目录定义类图Java经典实现懒汉Lazy Mode:饿汉Eager Mode:在饿汉下的多线程案例在懒汉下的多线程案例总结定义 单例模式(单件模式)确保一个类只有一个实例,并提供一个全局访问点。——HeadFirst 单例模式通过过防…...

机器学习中的公平性
文章目录机器学习公平性评估指标群体公平性指标个人公平性指标引起机器学习模型不公平的潜在因素提升机器学习模型公平性的措施机器学习公平性 定义: 机器学习公平性主要研究如何通过解决或缓解“不公平”来增加模型的公平性,以及如何确保模型的输出结果…...

Docker镜像之Docker Compose讲解
文章目录1 docker-compose1.1 compose编排工具简介1.2 安装docker-compose1.3 编排启动镜像1.4 haproxy代理后端docker容器1.5 安装socat 直接操作socket控制haproxy1.6 compose中yml 配置指令参考1.6.1 简单命令1.6.2 build1.6.3 depends_on1.6.4 deploy1.6.5 logging1.6.6 ne…...
蓝桥杯30天真题冲刺|题解报告|第三十天
大家好,我是snippet,今天是我们这次蓝桥省赛前一起刷题的最后一天了,今天打了一场力扣周赛,前面3个题都是有思路的,第三个题只过了一半的案例,后面看完大佬们的题解彻悟,下面是我今天的题解 目录…...

配置 Git Husky 代码提交约束
介绍 Git Husky 是一个可以管理 Git Hooks 的工具,它可以帮助我们在代码提交的时候运行脚本,以确保代码提交符合特定的规范和约定。 在 Git 中,允许在操作特定的事件时执行特定的脚本,这些事件我们称之为 Hooks。 Git Husky 利…...

IntelliJ IDEA 2023.1 最新变化
文章目录IntelliJ IDEA 2023.1 最新变化一. 主要更新1. 新 UI 增强 测试版启用新 UI2. 在项目打开时更早提供 IDE 功能3. 更快地导入 Maven 项目4.后台提交检查5. Spring Security 匹配器和请求映射的导航 Ultimate二. 用户体验1. 全 IDE 缩放2. 保存多个工具窗口布局的选项3. …...
stm32学习笔记-9 USART串口
9 USART串口 文章目录9 USART串口9.1 串口通信协议9.2 stm32的片上外设-USART9.3 USART收发相关实验9.3.1 实验1:串口发送9.3.2 实验2:移植printf函数9.3.3 实验3:串口发送接收9.4 USART串口数据包9.5 USART数据包相关实验9.5.1 实验1&#x…...

【蓝桥杯】每日四道编程题(两道真题+两道模拟)| 第四天
专栏: 蓝桥杯——每日四道编程题(两道真题两道模拟) “蓝桥杯就要开始了,这些题刷到就是赚到” ₍ᐢ..ᐢ₎♡ 另一个专栏: 蓝桥杯——每日四道填空题(两道真题两道模拟题) 目录 专栏࿱…...

大家有没有时候觉得,递归,分治,回溯,傻傻分不清楚?
递归,分治,回溯的定义 递归(Recursion) 递归是一种解决问题的方法,它将一个问题分解成一个或多个较小的相同类型的子问题,然后通过递归调用自身来解决这些子问题。递归通常包括一个基本情况(b…...

Java 8 - Lambda 表达式
1. 函数式接口 当一个接口中只有一个非 default 修饰的方法,这个接口就是一个函数式接口用 FunctionalInterface 标注 1)只有一个抽象方法 FunctionalInterface public interface MyInterface {void print(int x); } 2)只有一个抽象方法和…...

【Ruby学习笔记】4.Ruby 类和对象及类案例
前言 本章介绍Ruby的类和对象及类案例。 Ruby 类和对象 Ruby 是一种完美的面向对象编程语言。面向对象编程语言的特性包括: 数据封装数据抽象多态性继承 这些特性将在 面向对象的 Ruby 中进行讨论。 一个面向对象的程序,涉及到的类和对象。类是个别…...
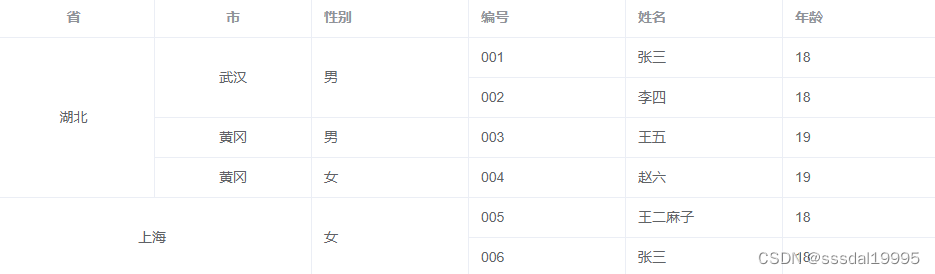
分享一个计算表格内单元格合并的工具,支持行合并、列合并等常见场景
分享一个计算表格内单元格合并的工具,支持行合并、列合并等常见场景 效果图 安装 cj-toolkit-x/table-cell-merger 插件 npm i cj-toolkit-x/table-cell-merger使用方法 import {TableCellMerger} from "cj-toolkit-x/table-cell-merger" // 创建一个单…...

CUDA编程(三):Hello world
CUDA编程(三):Hello worldCUDA编程Hello worldCUDA编程 CUDA是Compute Unified Device Architecture的缩写,由英伟达公司2007年开始推出,初衷是为GPU增加一个易用的编程接口,让开发者无需学习复杂的着色语…...
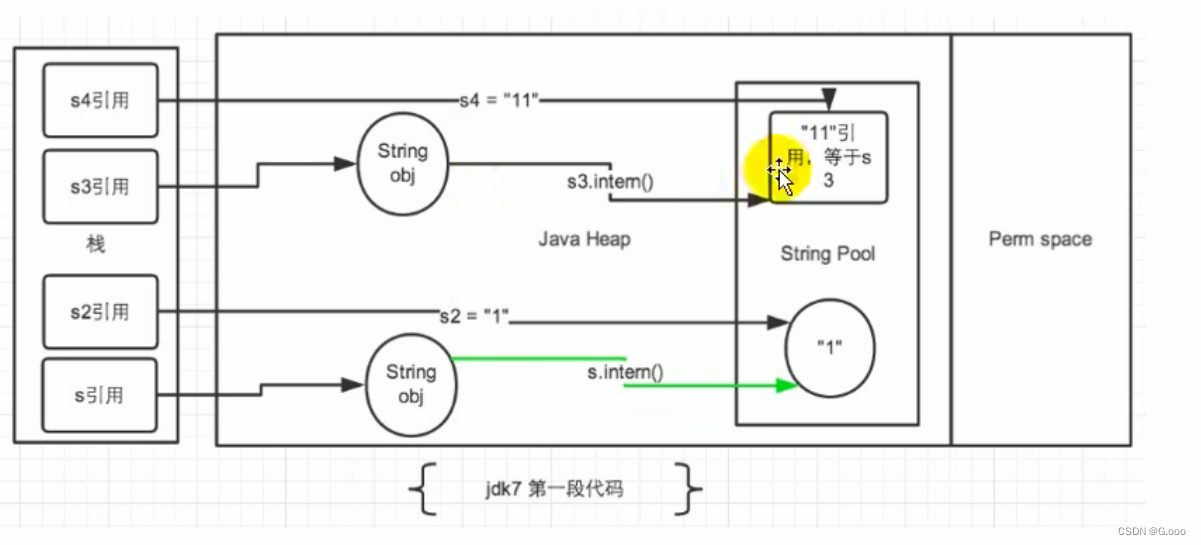
二十九、String的不可变性
一、String的基本特性 1.String:字符串,使用一对“”引起来表示 1)String s1 “hallo”; //字面量的定义方式 2)String 说 new String(“hello”)’ 2.String声明为final的,不可被继承。 3.String实现了Serialzable接口:表示字符串是支持序列化的。实…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

SQL进阶之旅 Day 22:批处理与游标优化
【SQL进阶之旅 Day 22】批处理与游标优化 文章简述(300字左右) 在数据库开发中,面对大量数据的处理任务时,单条SQL语句往往无法满足性能需求。本篇文章聚焦“批处理与游标优化”,深入探讨如何通过批量操作和游标技术提…...
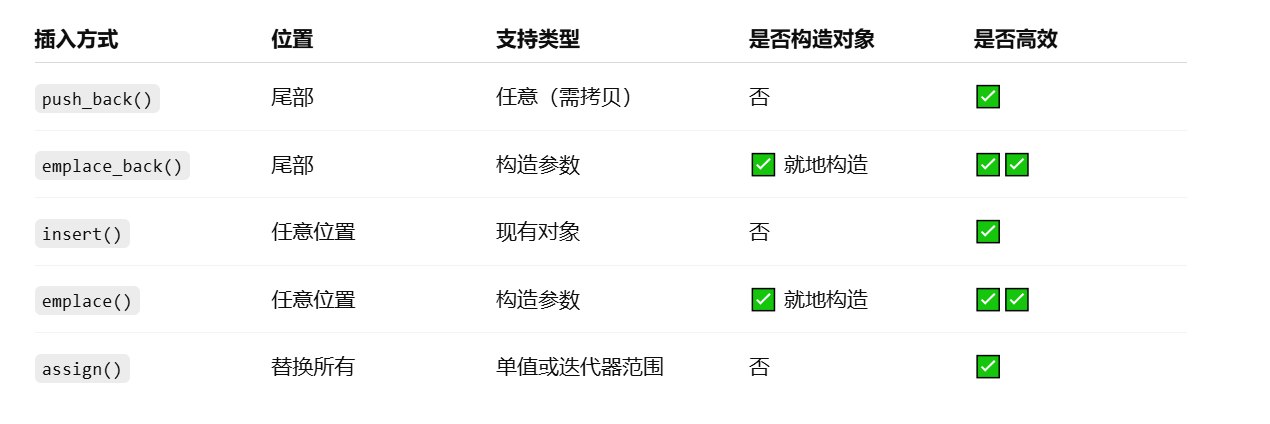
C++中vector类型的介绍和使用
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...
