掌控物体运动艺术：图扑 Easing 函数实践应用

现如今，前端开发除了构建功能性的网站和应用程序外，还需要创建具有吸引力且尤为流畅交互的用户界面，其中动画技术在其中发挥着至关重要的作用。在数字孪生领域，动画的应用显得尤为重要。数字孪生技术通过精确模拟现实世界中的对象、过程和系统，对动画的需求远远超过传统前端开发。

在这种环境中，动画不仅仅是为了美观，更是用于实现系统与现实的同步、演示复杂过程和数据可视化的关键手段。

HT 动画介绍

在足够短的时间内快速连续地改变物体的某个属性，人的眼睛会感知到物体在平滑移动，这种利用人类视觉持续性产生的效果就是动画。图扑自研 HT for Web 产品中提供了多种创建动画方式，其中很常见的是使用 ht.Default.startAnim 创建动画。

ht.Default.startAnim 支持两种动画模型：Frame-Based 和 Time-Based。这两种类型的动画所需的参数各不相同：

Frame-Based 帧动画具有固定的帧数，即 action 被调用的次数，创建动画时需传入一下参数：

• frames：动画的帧数。

• Interval：动画帧间隔毫秒数。‍‍

• easing：动画缓动函数，默认为 ht.Default.animEasing。‍

• finishFunc：动画完成后的回调函数。‍

• action：必须提供 action 函数，用于实现动画过程。第一个参数代表通过 easing 函数运算后的值，第二个参数代表当前动画进度（0~1）。

Time-Based 周期动画，动画帧数（action 的调用次数）取决于系统环境，创建动画需要传入的参数：

• duration：动画周期的毫秒数，默认使用 ht.Default.animDuration。

• easing：动画的缓动函数，默认使用 ht.Default.animEasing。

• finishFunc：动画结束时的回调函数。

• action：必须提供 action 函数，用于实现动画过程。

以小球落地过程为例，只需在动画过程中不断调整小球的位置属性，就能实现小球落地的动画效果：

const ball = dm.getDataByTag('ball'); // 获取小球节点
const elevation = ball.getElevation(); // 获取小球节点纵向位置
ht.Default.startAnim({duration: 1500,easing: t => t,finishFunc: function () { },action: function (v, t) {ball.setElevation(elevation - elevation * v); // 在动画中调整节点纵向位置}
​​​​​​​});

在上图中，小球的落地动画效果已实现，但动画看起来仍显得有些生硬。这是因为在现实中，小球落地是加速运动的，并且当小球接触地面后，受力变化会导致回弹。因此，我们还需要在动画中控制小球的速度和运动趋势，以便更真实地模拟这一过程。

那么如何在动画中控制速度呢？

这就需要引用下面的 easing 函数使用。

关于 Easing 函数

Easing（缓动函数）是用于调整动画速度的函数，它们定义了动画在开始、进行中和结束时的速度变化。这些函数允许动画以非线性方式运行，使动画效果更自然、流畅和有吸引力。缓动函数在坐标轴中的表现可以看作是一个以时间（t）为横轴、值为纵轴的图表。以下附图展示了一些常用的 easing 函数，从图中可以清晰地看到不同 easing 的变化趋势。

了解了 easing 函数的作用后，我们可以通过调整它来实现小球落地时的加速运动以及接触地面后的回弹效果。

ht.Default.startAnim({duration: 1500,easing: function (t) {const n1 = 7.5625;const d1 = 2.75;if (t < 1 / d1) {return n1 * t * t;} else if (t < 2 / d1) {return n1 * (t -= 1.5 / d1) * t + 0.75;} else if (t < 2.5 / d1) {return n1 * (t -= 2.25 / d1) * t + 0.9375;} else {return n1 * (t -= 2.625 / d1) * t + 0.984375;}},finishFunc: function () { },action: function (v, t) {ball.setElevation(elevation - elevation * v);}
});

在实际项目中，物体的运动通常较为复杂，因此我们需要根据不同的运动类型选择合适的 easing 函数。以下示例展示了在场景内的节点进行不同运动时，不同 easing 函数所产生的效果。

大家也可以该通过链接进行操作感受，通过切换不同的 easing 函数将呈现出不一样的动画效果：。

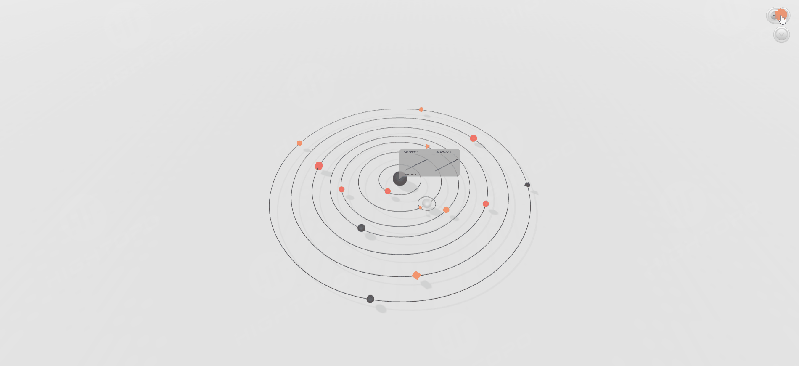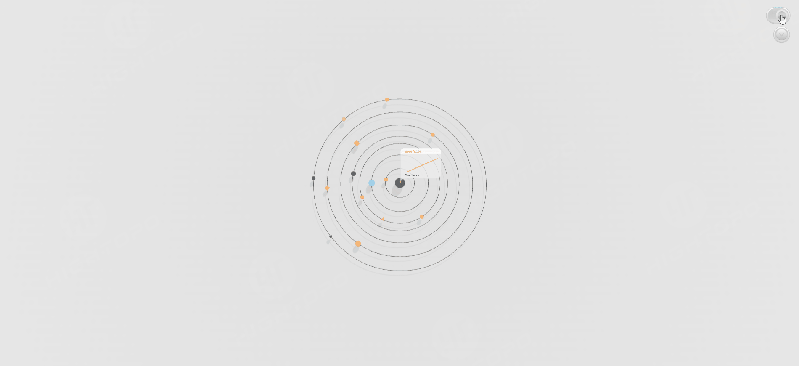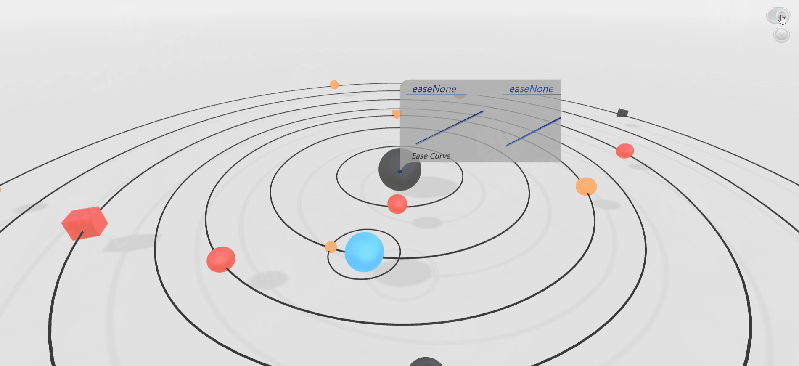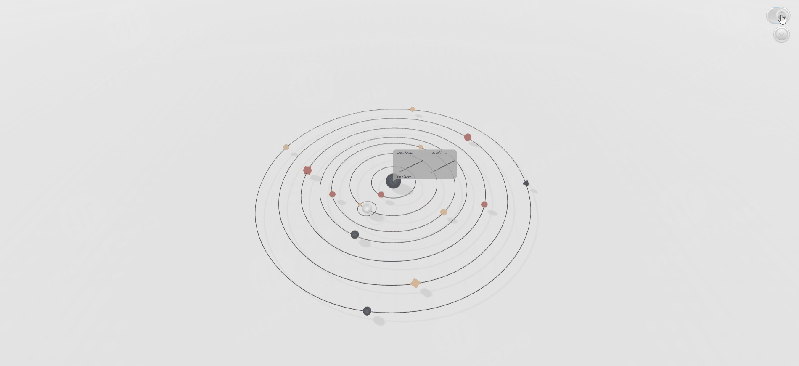
示例展示了多个动画的连续播放效果。我们可以在动画的 finishFunc 回调结束时，调用下一个动画，从而实现连续的动画效果。

ht.Default.startAnim({duration: 1500,easing: function (t) {......
},action: function (v, t) { ...... },finishFunc: function () {// 调用下一个动画ht.Default.startAnim({......})},});

常听人说 Easing 是动画的灵魂，就如同生命的节奏。有些人厚积薄发，有些人平稳一生，而也有些人起起伏伏，经历着高山低谷的跌宕起伏。无论过程如何多样精彩，终点都是一致的——正如动画中无论怎样变化的 Easing 曲线，最终都通向同一个终点帧。动画和人生一样，丰富的过渡和变化，赋予它们独特的美感和深意。